核心问题统领下度量一致性的教学策略

陈芸芸 方丽红

【摘   要】“角的度量”是“图形与几何”领域的重要教学内容之一，其教学目标是理解度量的本质。教师基于对“教学缺失了什么？”“学习忽视了什么？”的分析，以问题为统领，通过“提炼核心问题”“设计学习任务群”“构建递进式问题链”等策略，推进“时间与角度”的教学，引导学生感悟度量的内在一致性，促进学生思维的分层进阶，提升学生的量感素养及分析问题、解决问题的能力。

【关键词】核心问题；问题链；度量；量感

“角的度量”是“图形与几何”领域的重要教学内容之一，其教学目标是理解度量的本质，即被度量对象中含有多少个度量单位。教学这一内容时，教师需要引导学生运用已有的知识经验，基于对“角”的定性描述，通过定量刻画，深入理解“角”。另外，角度与钟面具有天然的联系。例如角的度量工具“量角器”是把圆平均分成360份，取其中的一半构成的。而钟面上的一大格是将圆平均分成12份，一小格则是将圆平均分成60份。这两者都指向度量单位的统一，体现了度量的一致性。因此，笔者尝试以核心问题为统领，将“时间”与“角度”整合起来进行教学。通过层层递进的问题链，驱动学生进行操作、探索和发现，感悟度量的内在一致性，促进学生的深度学习，从而实现学生思维的分层进阶。

一、研读教材：“角的度量”教学缺失了什么？

人教版教材在四年级上册编排了“角的度量”单元，主要包括两部分内容：一是线和角的认识，二是角的度量。在此之前，学生已在一维空间度量（长度）和二维空间度量（面积）的学习过程中积累了丰富的度量经验。但角的度量与长度、面积等的度量存在差异，它对学生而言是一个全新的知识领域。因此，有必要将其关联起来，促进学生感悟度量的一致性。

张奠宙教授将度量的本质归纳为“三性”，即正则性、有限可加性和运动不变性。其中，正则性是指度量标准与度量对象属性的一致性，并将度量标准规定为“1”。为了更好地把握角的度量的教学，笔者对人教版教材、苏教版教材和北师大版教材进行了横向比较（如表1），发现各版本教材都将“角的度量”安排在四年级上册，并且都包含以下内容：（1）提出统一度量单位的必要性，并对1°角进行描述；（2）引出度量工具——量角器；（3）给出量角的步骤。然而，这几个版本的教材均未对度量工具、度量步骤等背后的原理进行解释。换言之，教材内容在凸显度量本质方面存在缺失。

进一步比较三个版本教材在习题设计方面存在的差异，发现：人教版教材并未直接嵌入生活中角的度量的相关内容，而苏教版教材和北师大版教材则均将角的知识与生活实际相结合，引导学生运用角的度量这一学科知识解决生活中的问题。由此可见，人教版教材在生活中角的度量内容的编排上存在不足。

为此，笔者整合一至三年级的时间问题与四年级上册的角的度量的教学内容，设计了一节拓展课。通过探究“钟面上指针所表示的时间与角度关系”的活动，引导学生深入理解度量的本质，提升分析问题和解决问题的能力，全面发展量感这一核心素养。

二、研判学情：“角的度量”学习忽视了什么？

为了全面、准确地了解学生对“钟面上指针所表示的时间与角度关系”的认知水平，在完成“角的度量”单元内容的教学后，笔者针对本校四年级学生（使用人教版教材）展开了一次前测调查与分析。

（一）调查对象及方法

以本校四年级175名学生为调查对象，采用书面前测探究单的形式展开调查，要求学生在15分钟内独立完成。

（二）调查内容与分析

【前测题1】学习了“角的度量”相关知识后，你认为钟面上指针所表示的时间与角度之间存在联系吗？请举例说明。

本题旨在了解学生对“钟面上指针所表示的时间与角度关系”的认知情况，并考查学生这一认知的来源，初步掌握学生的认知基础。调查结果如表2所示。

表2 学生对“钟面上指针所表示的时间与角度关系”的认知情况

[前测题1       找联系

不知道钟面与角度有联系    知道分针与时针之间夹角度数的计算方法       知道分针与时针之间的夹角会随着时间而变化       知道特定时刻分针与时针之间的夹角度数       人数/人   11    39    108  17    百分比    6.29%     22.29%   61.71%   9.71%       ]

从表2来看，近90%的学生能在一定程度上认识到钟面上指针所表示的时间与角度之间存在联系。进一步分析学生的答题情况，发现有61.71%的学生仅能依赖“直角＝90°、平角＝180°”的认知，描述特定时刻钟面上的夹角度数。

【前测题2】请你用自己的话说一说，3时整钟面上分针与时针的夹角是多少度？你是怎么得到的？

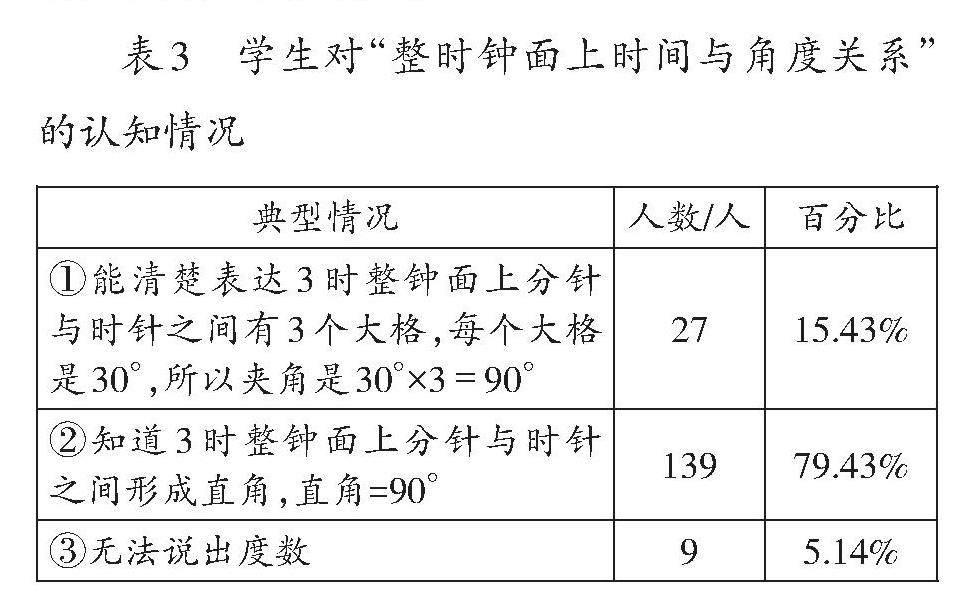
本题通过引导学生用语言描述3时整钟面上分针与时针之间夹角的度数，调查他们对整时钟面上分针与时针夹角度数度量情况的掌握程度，進而了解他们对时间与角度度量一致性的理解程度。调查结果如表3所示。

从表3中可以看出，大部分学生是基于“直角＝90°”的认知得出3时整钟面上分针与时针之间夹角的度数的。

综上所述，“角的度量”的学习活动忽视了两方面内容：一是角的度量与生活的联系，二是对角的度量本质的理解。因此，借助生活中熟悉的钟面，将时间度量与角度度量的本质建立联系，有助于进一步发展学生的量感，提升其分析问题与解决问题的能力。

三、教学实践：“角的度量”价值追寻的本质是什么？

“角的度量”价值追寻的本质是什么？为解决这一问题，笔者基于上述对教材和学情的分析，确立了拓展课的教学目标：通过“钟面上指针所表示的时间与角度关系”的探究活动，感悟度量的内在一致性，理解度量的本质，进一步提升量感素养，发展推理意识及分析问题、解决问题的能力。在教学过程中，笔者尝试以核心问题为统领，以问题链为主线，设置由浅入深的递进式问题链，驱动学生进行深度学习，将学生的思维逐步向纵深推进。

（一）提炼核心问题，明晰学习任务板块

核心问题是指针对教学目标和重难点所提出的关键问题。它不仅指向知识的本质，还具备提纲挈领的作用。在提炼核心问题时，首先要深入研读教材，明确教学目标及重难点，并结合学生实际情况，精心设计一组既相对独立又互相关联的核心问题，形成具有逻辑性和整体性的问题链，从而明晰学习任务板块。

例如，基于对教材和学情的分析，首先明确“时间与角度”拓展课的核心内容为钟面上指针所表示的时间与角度的关系，指向度量的本质。接着提炼出三个核心问题：（1）整时时刻，钟面上指针所表示的时间与角度具有怎样的关系？（2）半时时刻，钟面上指针所表示的时间与角度具有怎样的关系？（3）几时几分，钟面上指针所表示的时间与角度具有怎样的关系？（如图1）

这三个核心问题既具备独立的思考空间，又呈现出层层递进的态势。学生从对整时时刻时间与角度关系的初步感知，逐步深入对半时时刻时间与角度关系的理解，进而达到对几时几分时间与角度关系的有机拓展，知识内容得到有效外延。

（二）设计学习任务群，推进结构化学习

在设计学习任务群时，教师应以核心问题为中心，以提升学生自主探究能力为目标，同时关注学生在完成学习任务过程中的自主积极性，通过学习任务群驱动学生进行深度思考和全面探究，唤醒学生原有知识经验中与核心问题相关的知识、技能与方法，逐步实现“感知—领悟—内化”的结构化学习。

例如，对“时间与角度”中的三个核心问题进行分解，设计出“画一画、算一算、说一说”等学习任务群（如表4），既能引导学生逐步深入探究，又能激发学生的自主思考，强化对“钟面上指针所表示的时间与角度关系”的理解。

在此教学过程中，学生享有充分的思考时间、自主探究的空间以及充分表达的机会，能够全身心地投入到层次化的认知活动中，体验数学问题完整的探究过程，并建立核心问题之间的本质联系。

（三）构建递进式问题链，促进思维分层进阶

问题链是教学思路的具体化体现，具有较强的可操作性。在核心问题统领下，教师要设计具有逻辑关系的递进式问题链，为学生搭建一个个“问题台阶”，提供可视化支架，引发学生的主动思考与自主建构，使其理解层层深入，促进数学思维的分层进阶。

例如，针对核心问题2“半时时刻，钟面上指针所表示的时间与角度具有怎样的关系？”，教师可以设计以下子问题。

子问题①：观察这三个钟面，你有什么想说的？

教师先出示一个典型的错误作品（如图2），提问：“观察这三个钟面，你有什么想说的？”学生发现：三个钟面上的时针都画错了，三个半时的时针都没画到一大格的中间。

子问题②：从12时到12时半，分针走过半圈，时针走过多少度？

子问题③：12时半，分针与时针之间的夹角角度是怎么确定的？

子问题④：对比这三个半时时刻分针与时针之间的夹角度数，你有什么发现？

子问题⑤：半时时刻，分针与时针之间的夹角度数是怎么推导出来的？

在上述教学过程中，通过一系列子问题的逐一解决，学生逐步推导出半时时刻钟面上指针所表示的时间与角度的关系，并与整时时刻建立联系，初步构建“钟面上指针所表示的时间与角度关系”的数学模型。如此，教师以“浅入深出”的方式，引导学生深入学习，促使学生理解钟面上的度量一致性，进一步感悟度量的本质。

总之，问题链的设计驱动学生进行深度思考和充分探究，使深度学习成为现实。教师积极构建并实施递进式问题链教学，有助于学生深入理解知识的内涵和外延，为学生的知识获得和能力发展提供了充分的空间，从而发展其思维能力，培养其核心素养。

参考文献：

［1］鲍善军，朱曙光.“一题一课”的教学价值、设计与策略［J］.教学月刊·小学版（数学），2022（7/8）：12-16.

［2］鄭毓信.中国数学教育的“问题特色”［J］.数学教育学报，2018，27（1）：1-7.

［3］陈黎春.聚焦度量本质   促进量感发展：“角的度量”教学片断与思考［J］.小学数学教育，2023（22）：44-47.

（浙江省杭州市钱塘区河庄小学）