一类禽流感传染病传播模型的动力学分析

郭金生 薛梅

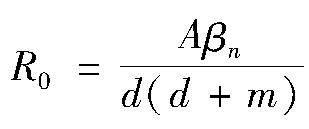
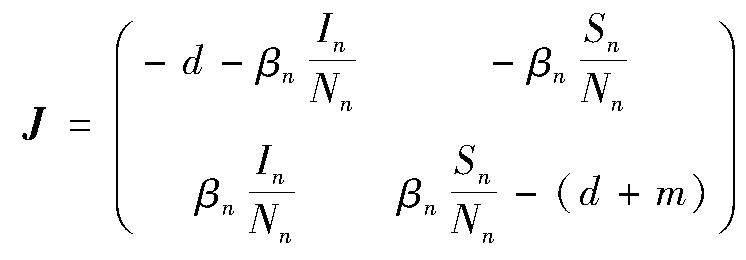
摘 要：以H7N9型禽流感为例，根据其传播具有潜伏期，研究了一类人-禽相互作用的H7N9型禽流感病毒的传播。针对此类传染病，构建了一类SI-SEIR型禽流感传染病传播的动力学模型，并利用该模型在人、畜环境中的多种病毒之间的相互作用，分析了无病平衡点和地方病平衡点的稳定性，对模型进行动力学分析，得到基本再生数R0。通过Lyapunov稳定性理论和LaSalle不变集原理，对模型的全局稳定性进行了分析，得出以下结论：当基本再生数R0小于1时，模型的无病平衡点全局渐近稳定；当基本再生数R0大于1时，模型的地方病平衡点全局渐近稳定。因此，在已经发生了禽流感疫情的地区，捕杀禽类和减少市场上禽类的流通等措施是杜绝此类传染病传播的关键。

关键词：动力学模型；动力学分析；基本再生数；全局渐近稳定

中图分类号：O175.1

文献标志码：A

近年来，由于全球范围内人口的快速增长，以及自然环境变化等各种因素的共同作用，埃博拉出血热、麻疹、疯牛病、禽流感等传染病的蔓延［1］，对人类的身体造成了很大的威胁。 如何预防和控制传染病一直都是人类面临的重大课题，如近年来在我国再次出现的H7N9型禽流感病毒。禽流感病毒与人流感病毒有着不同的特点，在正常情况下，它只能在禽类中进行传播，通常不会传染给人。郭树敏等［2-3］建立了具有完全饱和治疗率的数学模型，得出药物治疗在控制禽流感病毒扩散方面是可行的，并且在限制药物剂量的情况下，通过捕杀染病禽类能有效控制病毒在自然界中的传播。 本文重点在理论上对H7N9型禽流感传染病模型的动力学展开分析和研究，并在此基础上，通过构建一类SI-SEIR型禽流感传染病传播的动力学模型，对该病毒的传播规律、感染特性以及其扩散方式等进行分析。

1 模型的建立

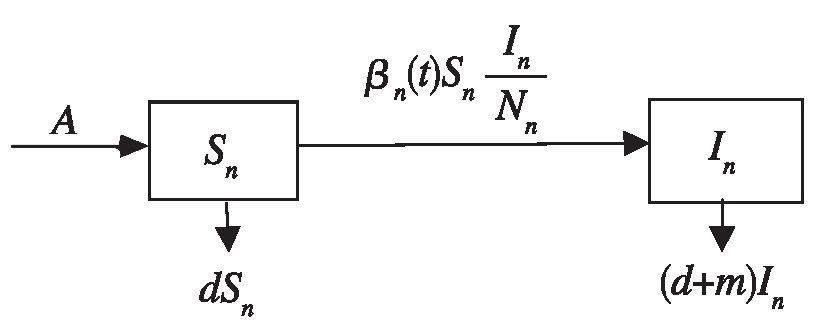
因为禽流感病毒的主要传播途径是通过染病禽类传播给人类，且其潜伏期较长，为了研究H7N9型禽流感的传播规律，可以考虑构建存在长潜伏期的人-禽相互作用的禽流感传播模型。鉴于禽类群体相对独立，受感染的人群不会直接对禽类造成威胁，因此有必要优先考虑禽类系统。这里，将禽类系统分为易感和感染两类，分别用Sn（t）和In（t）表示易感禽类与染病禽类在t时刻的数量，禽类系统的总数量为Nn（t）=Sn（t）+In（t）。在此，对其传播过程做如下假设：

则其对应的SI型传染病模型为

然后，对禽流感病毒在人群中的传播过程进行研究可知，H7N9型禽流感病毒主要是通过染病禽类和人类之间的接触而传播，病毒的潜伏期少于一个月。将人群分为易感人群、感染人群、潛伏人群和移除人群4类，将Sn+1（t）、En+1（t）、In+1（t）、Rn+1（t）记为其t时刻的人口数量。记Mn+1（t）=Sn+1（t）+En+1（t）+In+1（t）+Rn+1（t）为t时刻人类总数。假设其传播过程为

则其对应的SEIR染病模型为

其中，参数具体的详细说明如表1所示。

综上，给出如下SI-SEIR人-禽传染病模型

2 模型的分析

2.1 有界性

研究疾病传播的生物学意义，假设（Sn，In，Sn+1，En+1，In+1，Rn+1）∈R6+，由模型（3）可得

且其可行域为

定理1 若（Sn（0），In（0），Sn+1（0），En+1（0），In+1（0），Rn+1（0））∈R6+成立，那么式（3）的所有解是一致有界的。

2.2 禽类系统的稳定性分析

定义基本再生数

在R2+中，q0始终存在；当R0>1时，q+存在。

定理2［1］ 若R0<1，则q0在R2+上是全局渐近稳定的；若R0>1，则q+在R2+上是全局渐近稳定的。

证明 首先考虑无病平衡点q0，易得式（1）的Jacobian矩阵为

则在平衡点q0处的Jacobian矩阵为

下面考虑全局稳定。设Lyapunov函数为：

易知，当R0>1时，V′>0，平衡点q0在R2+上是不稳定的；当R0<1时，V′≤0。

显然，D1={（Sn，In）∈DV′=0}=（S0，0），可知式（1）在D上的最大不变集M只在集合D1中。从LaSalle不变性理论中可知，无病平衡点q0在R2+上是全局渐近稳定的，并且M=（S0，0）。

下面考虑地方病平衡点q+。如果R0>1，则地方病平衡点q+在R2+上存在。又式（1）在平衡点q+的Jacobian矩阵为

可知Jacobian矩阵Jq+的特征方程为

因而，式（1）不存在周期解，由定理1知正平衡点q+在R2+上是全局吸引的，故禽类系统的正平衡点q+在R2+上是全局渐近稳定的。

2.3 平衡点的存在性及稳定性分析

设平衡点为

令Sn（t）=0，In（t）=0，A（t）=0。

计算关于平衡点（S*n，I*n，A*）的Jacobian矩阵为

平衡点E*1的稳定性是由E*1点Jacobian矩阵的特征根确定的，所以若特征根中都存在负实部，则无病平衡点E*1是局部渐近稳定的。

引理1［4］ 当R0<1时，无病平衡点E*1是局部渐近稳定的；当R0>1时，无病平衡点E*1是不稳定的。

定理3［5］ 当R0<1时，无病平衡点E*1是全局渐近稳定的。

2.4 禽类-人类系统分析

定理4［1］ 若R0<1，则p0是局部渐近稳定的；若R0>1，则p0是不稳定的，但p+是局部渐近稳定的。

定理5 若R0<1，式（3）的无病平衡点p0是全局渐近稳定的。

证明 当R0<1时，无病平衡点p0是局部渐近稳定的，且

由定理2，结合极限系统理论［6］，知

即（3）是全局吸引的。故在R0<1时，无病平衡点p0在D0上是全局渐近稳定的。

下面讨论式（3）地方病平衡点p+的全局稳定性问题。

引理2［5］ 设（A1）χ是Rn+的一个紧子集，（A2）S是χ的一个紧子集。如果存在P∈C1（χP∈

C1（χ→Rn+），使得

（1） P（x）=0，x∈S；

（2） P′（x）>0，x∈S。

则充分大的T和常数k>0，使得对任意的0χ＼S和t≥T，存在P（x）>k的一个紧子集。

定理6 若R0>1，则式（3）是永久存在的。

证明 由定理1和定理4可知，存在T*，当t>T*时，存在kSn ，kIn ，KSn ，KIn，k及K，使Sn≥kSn，In≥kIn，及k≤N，M≤K。定义

Ω+={（Sn，In，Sn+1，En+1，In+1，Rn+1）Sn≥kSn，In≥kIn，k≤N，M≤K}

DS={（Sn，In，Sn+1，En+1，In+1，Rn+1）Sn≥kSn，In≥kIn，Sn+1=0，k≤N，M≤K}

可知，Ω+是R6+的紧子集，DS是Ω+的紧子集。

令P=S，那么P：Ω+→R+是C1的，当且仅当σ∈DS时有P（σ）=0。此外，对任何σ∈DS有P′（σ）>0。因此，由引理2知，存在正常数kS，使得对任意φ0∈Ω+＼DS，有

结合定理1知，存在KSn+1，使

同理可得，存在ki，Ki（i=En+1，In+1，Rn+1），使

故（3）是永久生存的。

3 初步应用

通过对一些数值进行模拟，研究一类具有突变影响且有潜伏性的人-禽相互作用的H7N9禽流感的传播；然后进一步验证以上的理论结果、数学模型的正确性及研究疾病的控制措施。

例1 设初始条件为禽类总数量都为N=1 000，禽类的初始感染者I=300，接触后传染的概率β=0.01，禽类的常数输入率A=2，禽的自然死亡率d=0.1，禽类由病毒引起的死亡率m=0.2；人类的总数量为N=1000，人类的初始感染者I=200，接触后传染的概率β=0.03，禽类的常数输入率B=0.2，人的自然死亡率μ=0.01，人类由病毒引起的死亡率δ=0.1，潜伏者转化为感染者概率ω=0.001，人的康复概率γ=0.1，则禽类系统的基本再生数R0=0.667<1，人类系统的基本再生数R0=0.286<1。在这组参数下，从图1和图2中可以看出，禽流感病毒在禽类中最终走向灭绝，在人类中最终也是趋于灭绝的。

例2 设初始条件为禽类总数量都为N=1 800，禽类的初始感染者I=600，接触后传染的概率β=0.5，禽类的常数输入率A=2，禽的自然死亡率d=0.2，禽类由病毒引起的死亡率m=0.8；人类的总数量为N=18，人类的初始感染者I=6，接触后传染的概率为β=0.01，禽类的常数输入率B=0.2，人的自然死亡率μ=0.001，人类由病毒引起的死亡率δ=0.3，潜伏者转化为感染者概率ω=0.01，人的康复概率γ=0.3，则禽类系统的基本再生数R0=5>1，人类系统的基本再生数R0=3.328>1。在这组参数下，如图3和图4所示，禽流感病毒在禽类系统中可以继续生存，在人类系统中也会持续存在。 因此，通过利用MATLAB进行数据模拟并作图，验证了该模型的合理性和应用性。

4 结论

本文以禽流感为研究对象，通过构建一个既考虑禽类群体动力学因素，又考虑人类群体动力学因素的具有潜伏效应及突变影响的SI-SEIR常微分方程模型，并根据禽类群体和人类群体两个群体的不同，选取不同群体的发病率。

利用传染病动力学基本再生数原理，对模型的局部和全局稳定性进行研究。 从计算结果可以看出，该模型的动力学性态是由病毒流行的基本再生数R0来确定。通过对该模型的分析可以得知，在基本再生数R0<1时，无病平衡点渐近稳定，病毒将消亡。当R0>1时，地方病平衡点是全局渐近稳定的，此时禽流感病毒将逐步变成地方病而存在。因此，在已经发生了禽流感疫情的地区，捕杀禽类和减少市场上禽类的流通等措施是杜绝此类传染病传播的关键［7］。此外，文中所建立的数学模型也存在很多未被考虑到的因素，如温度、湿度等，这些都将在未来的工作中加以探讨。

参考文献：

[1]趙亚飞. 禽流感传染病传播模型的动力学行为分析［D］. 重庆： 重庆理工大学， 2019.

［2］ 郭树敏， 郭丽娜， 李学志. 具有饱和治疗的禽流感动力学模型的研究［J］. 数学的实践与认识， 2010， 40（3）： 134-137.

［3］ 郭树敏， 李学志. 一类具有非线性传染率和有效治疗的HIV动力学模型的分析［J］. 韶关学院学报， 2015， 36（10）： 1-4.

［4］ 王红飞. 一类禽流感传染病数学模型的动力学行为分析［J］. 中国科教创新导刊， 2009（22）： 39-40.

［5］ 马知恩， 周义仓， 王稳地， 等. 传染病动力学的数学建模与研究［M］. 北京： 科学出版社， 2004： 22-89.

［6］ 纪振伟. 狂犬病和禽流感的动力学模型及控制策略研究［D］. 北京： 北京建筑大学， 2018.

［7］ 纪振伟， 许传青， 崔景安， 等. H7N9型禽流感传播模型的动力学分析［J］. 北京建筑大学学报， 2018， 34（1）： 64-69.

Kinetic Analysis of a Transmission Model of a Group of

Avian Influenza Infectious Diseases

Abstract：

In this paper， taking avian influenza H7N9 as an example， according to its incubation period， the transmission of H7N9 avian influenza virus with human-bird interaction is studied， and a kinetic model for the spread of SI-SEIR avian influenza is established. Then using the interaction among viruses in human， animal and environment， the stability of the disease free equilibrium and endemic equilibrium is analyzed， and the basic reproductive number R0 is obtained by kinetic analysis. Through the stability theory of Lyapunov and the principle of LaSalle invariant set， the global stability of the model is analyzed and the following conclusions are drawn： when R0 is less than 1， the disease free equilibrium is globally asymptotically stable; when R0 is greater than 1， the endemic equilibrium is globally asymptotically stable. Therefore， in areas where avian influenza outbreaks have already occurred， measures such as culling birds and reducing the circulation of birds in the market are key to stopping the spread of such infectious diseases.

Key words：

kinetic model; kinetic analysis; basic regenerative number; global asymptotic stability