重力驱动下漏斗出口形状及振动因素对颗粒流的影响分析

马鸿泽 郭涛 沙洁

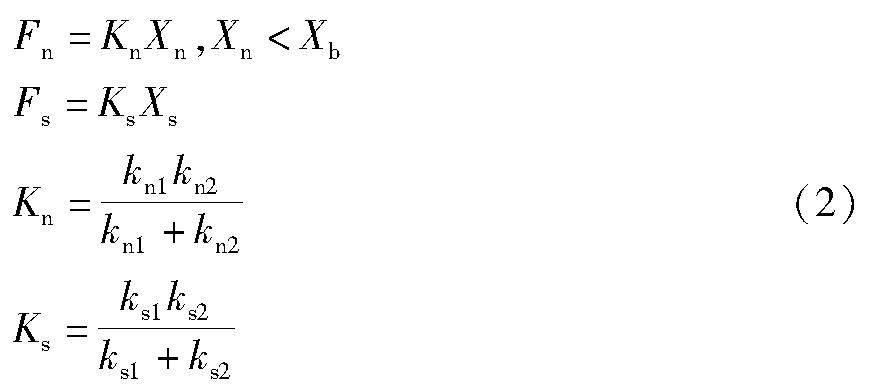
摘 要：为了深入了解漏斗颗粒在外部激励下的运动状态，本文基于离散元方法，探究了重力驱动下漏斗出口倾角、振动幅值、振动方向、颗粒竖向初始速度以及是否加装出口挡板对于颗粒流流量的影响。结果表明：出口倾角和振动幅值的增大都有利于颗粒流量的增加；在不考虑初始速度和挡板情况下，当振动方向由水平逐渐转向竖直这一过程中，颗粒流量随之减小，并且在水平方向振动时，颗粒流量达到最大值，而在加装出口挡板和考虑初始速度两种情况下，结果与之相反；在出口无挡板且振幅为零的条件下，赋予颗粒物质竖直方向速度有益于流量的增加，随着振幅的增大，流量稳步提高，但增长幅度均低于相同环境下无竖直方向速度的流量增长幅度；出口的挡板在低振幅下不利于颗粒物质的排出，但在提高振幅且振动方向逐步转向竖直方向后，颗粒流量大幅提高。

关键词：颗粒流；振动幅度；振动方向；流量；离散元

中图分类号：O311

文献标志码：A

颗粒物质是由大量具有宏观尺寸的粒子组成的相互作用的复杂集合体系。自然界中单个颗粒的尺寸一般在10-6～10 m之间，其颗粒的运动情况遵从牛顿定律。当它们静止时，颗粒物质呈固态。当收到外界能量的扰动，产生流动时，具有类似于流体的运动方式，通常称为颗粒流，其广泛存在于自然环境中的泥石流［1］、雪崩［2］、岩土体滑坡［3-4］、沙丘迁移［5］、交通流［6］、以及离散物料的加工、输运、存储等工业生产中［7］。如，筒仓中的粮食出料动力学行为。美国《Science》［8］杂志将“颗粒流动力学理论”列为当今125个重大科学问题之一，2014年出版的《中国学科发展战略：流体动力学》［9］也将“颗粒物质与颗粒流”列为6个基础与前沿学科之一。由此可见，探究并认识颗粒物质的运动规律和本质具有较大的实际工程应用和科学意义。

颗粒流根据其流动形态，可分为漏斗流、斜坡流、转筒流和堆积流等，其中，漏斗流因其应用灵活的特性和复杂的相应机制一直被视为颗粒流问题中重要的研究领域［10-12］。广义上来讲，任何一种从广口导入，小口流出的装置都可视为漏斗，在此装置中的颗粒流便叫做漏斗流。1961年荷兰物理学家BEVERLOO ［13］推出了著名的颗粒流流量公式——Beverloo公式，此后颗粒流流量就成为探究颗粒流运动状态的重要指标之一。KOHRING等［14］模拟了2D状态下方形颗粒在漏斗中的流出情况，研究发现不同流入速率下，出口流量表现为不稳定状态，最后中断流出、堵塞出口；ASHOUR等［15］观察了各种形状颗粒在3D漏斗中的流出状态，发现颗粒长宽比的增加降低了流速且增加了出口堵塞概率；WANG等［16］的研究也证实椭球长宽比的增加不利于出口流量的增大；KOIVISTO等［17］对比了表面粗糙和表面光滑这两种颗粒的流出状况，发现光滑颗粒流量随着颗粒填充高度的减少而减少，但表面粗糙颗粒因为摩擦力的存在使得其出口速度为一个恒定的数值，漏斗属性也是改变颗粒流流量情况的重要依据；JANDA等［18］的研究表明，在二维情况下，当出口尺寸缩小到约为颗粒直径的4倍时，流动可能会停止，发生堵塞的几率急剧增加；WAN等［19］考虑了出口形状对颗粒流流量的影响，发现流量随出口曲率变大而增加，由此修正了内孔为圆弧面时的BEVERLOO公式；黄德财等［20］研究了开口角度对二维颗粒流流量的影響，结果发现，无论是在固定入口流量还是固定颗粒数目的情况下，开口角度的增大可以提高颗粒流出口流量和出口流速；YU等［21］采用了离散元法研究了颗粒壁面静摩擦系数对颗粒流态和速度分布的影响，结果表明，静摩擦系数对壁面区域的速度分布有明显的影响，随着静摩擦系数的增大，流动形态由质量流转变为漏斗流，壁面剪切层变大变宽，外部条件也会影响颗粒流流量的变化；DORBOLO等［22］使用离心机探究重力对筒仓出料的影响，探究了失重和超重的环境中筒仓的出口流量，结果表明，超重的环境有利于流量的提升，但对确定允许颗粒流出的最小出口尺寸影响不大。

颗粒流有三种情况：稀疏流、密集流和堵塞。稀疏流是指颗粒堆积密度较低，整体流速较高、颗粒之间几乎没有相互作用的颗粒流；密集流是指颗粒堆积密度较高、整体流速缓慢、颗粒之间多为相互碰撞、挤压的颗粒流；随着颗粒堆积密度继续增大，颗粒之间的相互作用力不断变大，在局部区域内形成力拱，截停颗粒流，致使颗粒不再流动，从而发生堵塞现象。力拱结构并不稳定，有时可以自行崩塌，使颗粒继续流动［23］，有时要通过外部激励如碰撞、振动等破坏力拱。HUNT［24-25］等通过实验装置对料斗施加了水平方向和竖直方向的振动，通过分析发现，两种方向的振动降低了力拱形成的概率、增加颗粒流流量、减少停滞地带。

然而，在实际生产加工中，颗粒有时并非从静止状态开始出仓，工厂所用的漏斗装置不尽相同，为了提高出口流量施加的振动幅值也参差不齐、振动方向更是千差万别。目前少有文献对以上情况进行综合研究。本文基于离散元方法，在2D重力驱动的漏斗流模式下，探究了出口倾角、振动幅值、振动方向、颗粒竖直方向初始速度以及是否加装出口挡板对于颗粒流流量的影响。

1 离散元理论

CUNDALL等［26］在1979年首次提出离散元法，其基本思想是将物体看做由多个非连续体分离而成刚性单元的集合，且每个刚性单元都服从牛顿第二定律，其与分子动力学相似却又不同，分子动力学只需描述原子在给定相互作用力下的运动规律，而离散元还要考虑单元固有性质（密度、粒径等）、物体性质（粒径分布、孔隙率等）和单元的运动和旋转。单元的基本运动方程为

mx··（t）+cx·（t）+kx（t）=f（t）（1）

式中：m为单元质量；x为位移；t为时间；c为黏性阻尼系数；k为刚度系数；f为单元所受外荷载。

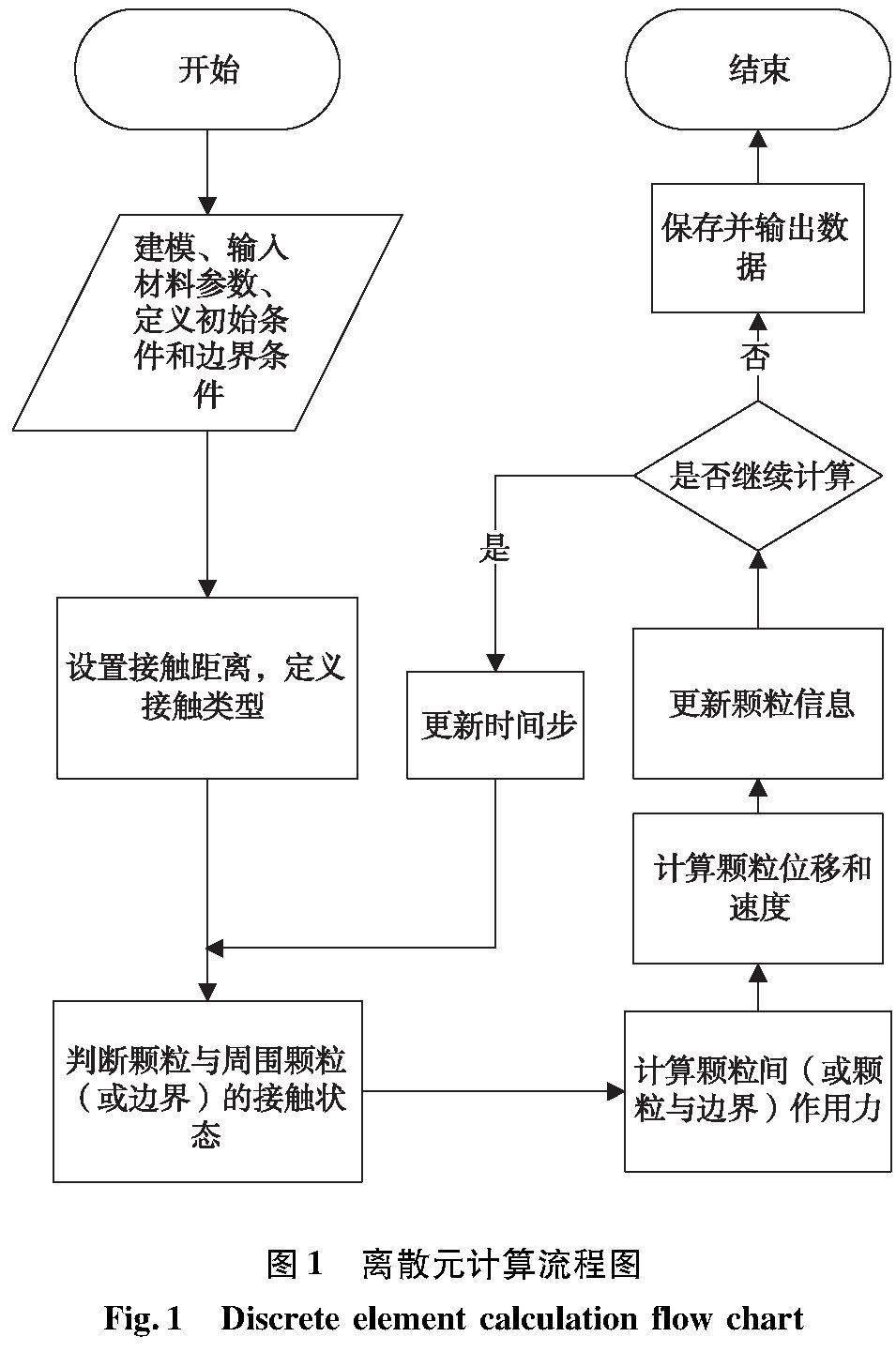
离散元法最初被用于分析块体岩石系统和岩土体边坡在准静力、动力条件下的力学行为问题。目前，由于离散元理论的不断发展和计算机技术的进步，离散元法已广泛的应用到各个领域［27-29］，已成为解决颗粒物质、颗粒流问题的主要手段。其计算流程如图1所示。

本文视颗粒为刚体，赋予颗粒间线弹性模型以考虑其相互的挤压、碰撞和摩擦这三种作用［30］，如图2所示。公式（2）为颗粒间法、切向力的计算公式。

式中：Fn、Fs为法向、切向力；Kn、Ks为法向、切向刚度；kn1、kn2分别为两个接触小球各自的法向刚度；ks1、ks2分别为两个接触小球各自的切向刚度；Xn，Xs为法向、切向相对位移；Xb为断裂位移。当颗粒之间的变形超过断裂位移时，颗粒分离，不考虑两者相互作用。

颗粒之间的切向相互作用效应，采用莫尔-库伦准则，即

Fs max=Fs0－μpFn（3）

式中：Fs max为最大剪切力；μp为颗粒间摩擦系数；Fs0为没有施加法向力时，颗粒间所能承受的最大抗剪力。当切向力超过最大抗剪力，切向弹簧断裂，此时颗粒间只存在滑动摩擦力－μpFn。

2 数值模型

本文漏斗流模型尺寸如图3所示，由漏斗壁和颗粒群共同组成。单颗粒质量为m=0.84 g，颗粒直径d=10 mm，出口尺寸与颗粒直径之比D0/d=10>4，以防止出口尺寸过小而堵塞颗粒流动。颗粒与容器壁摩擦系数μpw和颗粒间摩擦系数均为μ=0.4，颗粒间的法向刚度Kn=7.12×106 KN/m，切向刚度Ks=4×106 KN/m。

颗粒从入口上方由重力（g=9.8 m/s2）作用做自由落体运动，堆积到出口封闭的漏斗装置中，一段时间后，颗粒堆积形状如图3 阴影部分所示，以此模拟自然堆积的初始状态，此时颗粒速度为零，颗粒之间相互作用力微弱，再打开漏斗出口，使颗粒物质下落。考虑初始速度V0=0 m/s（静止）和V0=－1 m/s两种初始状态下的颗粒流动，竖向初始速度V0的控制方法是将自然堆积状态下的颗粒群统一抬升一定高度，自由释放获取速度。

另外，计算中还考虑了左右两侧漏斗壁相同方向、幅值下的振动和出口倾角θ对出口颗粒流量的影响。α为振动方向与X轴的夹角，0°≤α≤90°α=0°时为水平振动，α=90°时为竖直振动；漏斗壁振动形式以正弦函数Asin（10T0π/180）控制（A为振动幅值、T0为时间步）。

3 结果分析

3.1 无振动情况下颗粒流速分析

在不考虑振动的情况下，探究改变漏斗出口倾角θ、加装出口挡板L和颗粒初始速度V0等因素对颗粒流速的影响，其结果如图4、图5所示。

由图4可知，无论是否增加出口挡板，还是赋予颗粒竖直方向初速度，出口倾角的增加都有利于颗粒的流出。出口越陡峭，颗粒流出的质量越多。如图5所示，在颗粒滚动的过程中，斜边方向上颗粒重力的两个分量Mgsin θ和Mgcos θ，分别提供驱动颗粒运动的动力和阻碍颗粒运动的摩擦力，当θ不断增大，两个分量此消彼长，数值差距不断增大，致使颗粒的获得加速度越来越大，最终实现流量的增大。拥有初始速度V0的颗粒流量更大，比V0=0 m/s的情况下的颗粒流量提高了52%～69%。

图6为无振动情况下，最快下落20个颗粒的平均坚直方向速度图。从图4、图6 的数据可以判断，竖直挡板对于颗粒的加速具有负作用，竖直挡板与出口构成了一个狭小的矩形区域，颗粒在流过此区域时，活动空间变小、水平方向约束加强，增加了颗粒与颗粒之间碰撞、挤压，颗粒与挡板之间的摩擦力也随之增强，导致颗粒向下运动受阻，同比于不加装数值挡板的装置来说，加装出口挡板后流量和流速分别降低了约11%～23%、5%～19%。

3.2 振动情况下颗粒流速分析

图7为漏斗不同振动方向下颗粒的运动趋势图。由图7可看出，振动方向由水平转向竖直方向时大致可分为三个情况。

（1）第一种情况，当α=0°时（水平振动），处于左侧的颗粒会跟随壁面一同向右运动。受到挤压作用，左壁附近的颗粒相对更密集，阻碍了颗粒的流动。而此时右壁向右移动之后，壁和颗粒之间存在一定空隙，由于与壁面分离，颗粒约束减弱，右侧粒子在重力作用下可以快速的向右下方移动，如图7（a）。

（2）第二种情况，当α=θ时，振动方向与漏斗壁平行。此时，漏斗左壁附近的颗粒会随着壁面一起向右上方运动，但右壁附近的颗粒却沿着壁面向下滚动，不受右壁运动的影响。在这种情况下，左壁将附近的颗粒向上抬升了一定的距离，相当于延缓了颗粒下落的时间。但右壁向上移动后，缩短了右壁颗粒与出口之间的距离，使此部分颗粒更快流出，如圖7（b）所示。

（3）第三种情况，α>θ时，左右壁附近的颗粒运动情况相似，由于撞击、挤压的作用各个颗粒都随壁面向右上移动，如图7（c）所示。

在经历了多次振动后，颗粒之间的分界线已经模糊，各层颗粒通过运动后相互交错在一起，上层的颗粒落入下层，下层的颗粒运动到上层，如图8所示。因此，可以将竖向振动看做是加快颗粒运动到不同层级的一种方式，而这种方式无疑是有利于颗粒流出。

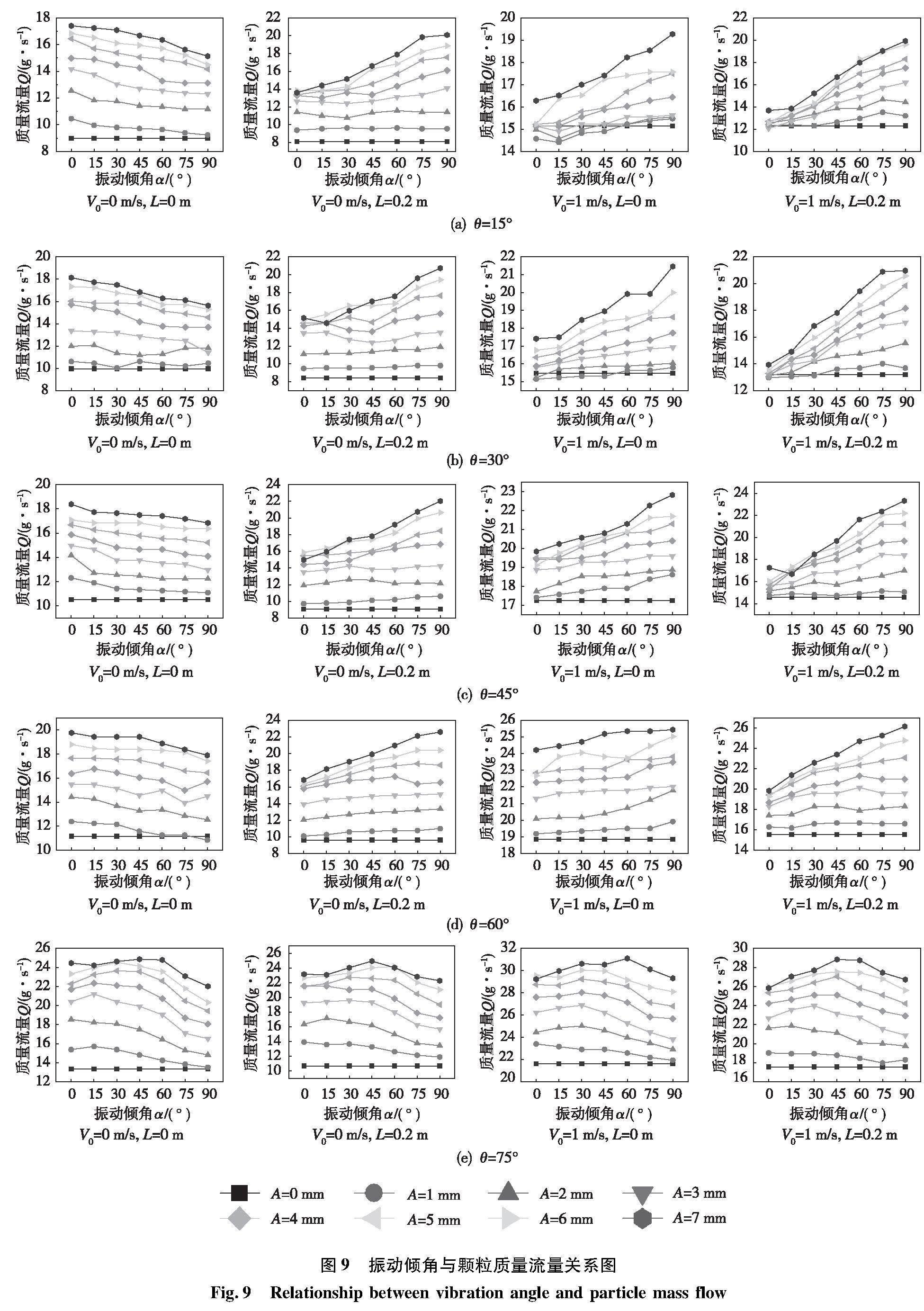
图9为改变振动方向、振动幅值、出口倾角等影响因素下，颗粒的流量变化。从结果可知：（1）无论如何更改振动方向、出口倾角，振动总是能加速颗粒的流出，并且振幅A越大，效果越明显，随着振动幅值A的增加，在第一和第二中情况下颗粒能较快地流出漏斗。在无竖向初始速度和不加装出口挡板的情况下，水平方向振动时流出颗粒的流量总是最大，且随着振动方向逐渐转为竖直时而减小。

（2）在不考虑初始速度和挡板（V0=0 m/s，L=0 m）、不考虑初始速度+挡板（V0=0 m/s，L=0.2 m）、考虑初始速度+无挡板（V0=－1 m/s，L=0 m）、考虑初始速度+挡板（V0=－1 m/s，L=0.2 m）四种工况下，随着出口倾角θ的不断增加，颗粒的流量与振动倾角α的变化曲线越来越平缓。在V0=0 m/s，L=0 m况中，相同振动幅值下，出口倾角对颗粒流量影响较小。但是在其他三种工况中，当振动幅度A≥3 mm时，振动角度α对颗粒流量影响较大，流量随α的增加而增加。

（3）在颗粒具有竖直方向初速度后，在流经振动过程中的漏斗时，增加了颗粒撞击壁面的概率，由于颗粒与壁面、颗粒间的碰撞、挤压阻碍了颗粒的向下运动。因此，在颗粒具有竖直方向初速度的情况下，水平振动流出的颗粒质量反而最小，竖直振动流出的颗粒质量最大。

（4）总体而言，考虑初始速度及无挡板（V0=－1 m/s，L=0 m）的情况，颗粒流出效率较优。水平振动下加装挡板，阻碍颗粒的流出。而竖直振动下加装挡板则增加颗粒的流出，且竖直振动时，加装挡板的影响有限。

（5）当出口倾角θ=75°时，颗粒流出质量的趋势除了在V0=0 m/s，L=0 m工况下与其他出口倾角的趋势相同外，其他工况均是先涨后落，如图9（e）所示。主要由于当出口倾角θ=75°时，壁面近似竖立，颗粒可以活动的区域较为狭窄，当壁面开始水平方向振动时，颗粒水平向加速度较大，颗粒之间相互作用力增强，挤压、碰撞的概率变大，减缓颗粒流出。随着振动方向的变化，颗粒在水平方向上获得的速度逐渐减少，在振动倾角α=60°左右时，加速颗粒向漏斗中心线聚拢，又不与其他颗粒发生激烈的碰撞，使其更快流出装置。

4 结论

本文基于离散元方法，在重力驱动的漏斗流模式下，探究出口倾角、振动幅值、振动方向、颗粒竖直方向速度以及是否加装出口挡板对于颗粒流流量的影响。结果表明：

1）出口倾角增加和赋予颗粒竖直向下方向速度都可以加快颗粒从漏斗装置流出，虽然在出口加装竖直挡板有利于颗粒流出后的堆积，但两侧挡板之间的空间十分狭隘，不利于颗粒的流出。

2）在不改变振动方向的情况下，振动幅值越大越有利于颗粒的逃逸，装置振动可以使颗粒获取速度，加快颗粒从其他位置运动到出口的过程，减少形成力拱的概率。

3）振動的方向不同，振动后的作用效果也不同，在只改变出口倾角的情况下，水平振动最有利于颗粒的流出，但是在颗粒有竖直向下方向和漏斗出口有竖直挡板时，竖直振动对颗粒运动方向的改变量最小，此时颗粒流出质量最大。

参考文献：

[1]ZHOU G G D， DU J H， SONG D R. et al. Numerical study of granular debris flow run-up against slit dams by discrete element method［J］. Landslides， 2020，17（3）： 585-595.

［2］ HU Y X， LIH B， QI S C. et al. Granular effects on depositional processes of debris avalanches［J］. KSCE Journal of Civil Engineering， 2022， 24（4）： 1116-1127.

［3］CHEN Z， SONG D Q. Numerical investigation of the recent Chenhecun landslide （Gansu， China） using the discrete element method［J］. Natural Hazards， 2021， 105（1）： 717-733

［4］ 陈古华， 韩培锋， 王月明， 等. 拦挡桩群对滑坡碎屑流挡流效果的离散元模拟［J］. 铁道科学与工程学报， 2022， 19（1）： 129-140.

［5］ AN A J， NIE Z H. Quantification of shape properties and their effects on particle packing of coarse-grain soil［J］. Indian Geotechnical Journal， 2021， 51（2）： 405-413.

［6］ 崔曼， 薛惠锋， 陈福振， 等. 道路交通的流体物理模型与粒子仿真方法［J］. 物理学报， 2017， 66（22）： 227-240.

［7］ TIVADAR P， BO F， DARIEL H D， et al. The role of the particle aspect ratio in the discharge of a narrow silo［J］. New Journal of Physics， 2022， 24（10）： 103036.1-103036.13.

［8］ SEIFE C. Can the laws of physics be unified？［J］. Science， 2005， 309：82.

［9］ 中国科学院. 中国学科发展战略：流体动力学［M］. 北京： 科学出版社， 2014.

［10］ZHU H P， ZHOU Z Y， YANG R Y et al. Discrete particle simulation of particulate systems： theoretical developments［J］. Chemical Engineering Science， 2008， 62（13）： 3378-3396.

［11］LETURIA M， BENALI M， LAGARDE S， et al. Characterization of flow properties of cohesive powders： a comparative study of traditional and new testing methods［J］. Powder Technology， 2014， 253： 406-423.

［12］郑宁， 朱红伟， 黄德财， 等.漏斗颗粒流的物理因素影响研究［J］. 中国科学：物理学 力学 天文学， 2020， 50（9）： 70-91

［13］BEVERLOO W A. The flow of granular solids through orifices. Chemical［J］ Engineering Science， 1961， 15： 3-4.

［14］KOHRING G A， MELIN S， PUHL H， et al. Computer simulations of critical， non-stationary granular flow through a hopper［J］. Computer Methods in Applied Mechanics and Engineering， 1995， 124（3）： 273-281.

［15］ASHOUR A， WEGNER S， TRITTEL T， et al. Outflow and clogging of shape-anisotropic grains in hoppers with small apertures［J］. Soft Matter， 2017， 13（2）： 402-414.

［16］WANG S Q， FAN Y N， JI S Y. Interaction between super-quadric particles and triangular elements and its application to hopper discharge［J］. Powder Technology， 2018， 339： 534-549.

［17］KOIVISTO J， KORHONEN M， ALAVA M， et al. Friction controls even submerged granular flows［J］. Soft matter， 2017， 13（41）： 7657-7664.

［18］JANDA A， HARICH R， ZURIGUEL I， et al. A Flow-rate fluctuations in the outpouring of grains from a two-dimensional silo［J］. Physical Review E Statistical Nonlinear & Soft Matter Physics， 2009， 79（3）： 031302.1-031302.5.

［19］WAN J F， WANG F G， YANG GH， et al. The influence of orifice shape on the flow rate： a DEM and experimental research in 3D hopper granular flows［J］. Powder Technology， 2018， 335： 147-155.

［20］黃德财， 胡凤兰， 邓开明， 等. 开口角度对二维颗粒流稀疏流-密集流转变的影响［J］. 物理学报， 2010，59（11）： 8249-8254

［21］YU Y， SAXN H. Discrete element method simulation of properties of a 3D conical hopper with mono-sized spheres［J］. Advanced Powder Technology， 2010， 22（3）： 324-331.

［22］DORBOLO S， MAQUET L， BRANDENBOURGER M， et al. Influence of the gravity on the discharge of a silo［J］. Granular Matter， 2013， 15（3）： 263-273.

［23］ZHANG S， GE W， CHEN G J. et al. Numerical investigation on the clogging-collapsing events in granular discharge［J］. Powder Technology， 2022，408 ：117714.

［24］HUNT M L， WEATHERS R C， LEE A T， et al. Effects of horizontal vibration on hopper flows of granular materials［J］. Physics of Fluids， 1999， 11（1）： 68-75.

［25］WASSGREN C R， HUNT M L， FREESE P J， et al. Effects of vertical vibration on hopper flows of granular material［J］. Physics of Fluids， 2002， 14（10）： 3439-3448.

［26］CUNDALL P A， STRACK O D L. A discrete numerical model for granular assemblies［J］. Geótechnique， 1979， 16（4）： 77.

［27］曾智伟， 马旭， 曹秀龙， 等. 离散元法在农业工程研究中的应用现状和展望［J］. 农业机械学报， 2021， 52（4） ：1-20.

［28］周先齐， 徐卫亚， 钮新强， 等. 离散单元法研究进展及应用综述［J］. 岩土力学， 2007， 28（增刊1）： 408-416.

［29］南文光， 顾益青， MOJTABA G. 增材制造中金属粉末卡塞动力学离散元模拟研究［J］. 工程热物理学报， 2022， 43（5）： 1260-1266.

［30］劉春. 地质与岩土工程矩阵离散元分析［M］. 北京： 科学出版社， 2019.

Analysis of the Effect of Funnel Outlet Shape and Vibration

Factors on Particle Mass Flow under Gravity

Abstract：

In order to gain a deeper understanding of the motion state of funnel particles under external excitation， this paper， based on the discrete element method， explores the influence of outlet dip ngle， vibration amplitude， vibration direction， vertical velocity of particles and whether to install the outlet bundle device on the particle flow rate under the gravity-driven funnel flow mode. The experimental results show that the increase of outlet angle and vibration amplitude is conducive to the increase of particle flow rate. Without considering the initial velocity and baffle， as the vibration direction gradually shifts from horizontal to vertical， the particle flow rate decreases accordingly. When the vibration direction is horizontal， the particle flow rate reaches the maximum value. However， the result is opposite when the bunching device is installed and the vertical velocity is set. Under the condition that the outlet is not bunching and the amplitude is zero， the vertical velocity is beneficial to the increase of the flow rate. With the increase of the amplitude， the flow rate increases steadily， but the growth rate is lower than that of the flow rate without vertical velocity in the same environment. The baffle at the outlet is not conducive to the discharge of particulate matter under low amplitude， but after increasing the amplitude and gradually turning the vibration direction towards the vertical direction， the particle flow rate increases significantly.

Key words：

particle flow; vibration amplitude; vibration direction; flow; discrete element