“循源而学”理论视域下的小学数学教学：看见数学、理解数学、学通数学、用好数学

［摘 要］ 如何提高小学生数学学习兴趣、提升学生数学学习力、体悟数学的价值是当前小学数学教育三大待解难题。解决之道在于让学生看见数学、理解数学、学通数学、学好数学、用好数学、爱上数学，“循源而学”应运而生。它倡导顺着数学产生、发展、应用的“源”与“流”而学，其核心内容包括循数学发展之源而学、循人生成长之源而学、循生存生活之源而学，体现为从数学学习走向人生成长、从人生成长走向完整生活，这是一切学科学习的基本“源”与“流”，是系列内化与外化、专与博、立己与达人、出发与归宿、基础与发展的自然生长、生发、生态过程。“情境与问题、体验与实践、关联与综合、拓展与长程、创造与成长”是“循源而学”的五大设计与实施要义。

［关键词］ 循源而学；看见数学；理解数学；学通数学；用好数学

［中图分类号］  G622.0  ［文献标识码］ A  ［文章编号］ 1005-5843（2024）03-0151-06

［DOI］  10.13980/j.cnki.xdjykx.2024.03.023

法国数学家拉普拉斯曾说，“数学是科学的基础，也是所有学问的灵魂”。义务教育数学课程标准中明确指出：“数学在形成人的理性思维、科学精神和促进个人智力发展中发挥着不可替代的作用。数学素养是现代社会每一个公民应当具备的基本素养。”［1］

然而数学在小学生心中的印象是枯燥的、抽象难懂的，除一些计算价值外似乎没有多大用处。如何激发小学生的数学学习兴趣、提升数学学习力、感受数学的价值是当下小学数学教育亟待破解的三大难题。最终如何真正让学生从小看见数学、理解数学、学通数学，进而学好数学、用好数学、爱上数学［2］，“循源而学”理论的提出正是对此的探索与实践。

一、“循源而学”的提出

如何提升兴趣、提升数学学习力、感受数学的价值，本质就是要让学生从小感悟数学到底是什么、怎么产生的、如何不断发展的、可以用来干什么，这样才能既见树木又见森林，既识表象又见本质，既通术器也明道法，才能真正像学科专家一样思考与学习，才能从知识的容器走向知识的创造者，才能从死记硬背走向举一反三、活学活用。数学学习的兴趣不在外在，而在数学内容本身；数学的价值不在他处，而在数学内容本身。所以关键就在于学生看见数学、学通数学，知其然且知其所以然，便能从学会走向会学。

（一）提升学习的效能：因循学科发展本质而学

要实现数学育人价值，首先需要让学生看见数学、理解数学、学通数学、爱上数学。学生觉得数学枯燥、抽象，是因为他们看到的是冰冷的符号，没有看到符号背后鲜活的数学生长和发展过程。所以解决难、烦、杂的问题，贵在让学生厘清数学的产生、发展脉络，沿着数学发展的本质、顺着数学建构的逻辑进行学习，顺藤摸瓜，而非见子打子。这样每一次的新学并非绝对意义上的重新学习，而只是基于房屋地基、房屋框架基础上的添砖加瓦，装修美化。一线数学教育一定要破除零散碎片化地教，而要让学生学一课通一片、学一片通全局，提升学习效能，做到迁移理解，自主建构，举一反三。“循源而学”倡导顺着数学产生、发展的“源流”而学，正是对三大数学教育关键难题破解之策的高度凝练。

（二）应对未来变化的当下行动：以数学学习为载体，发展学生的核心素养

会学数学是数学教育的重要内容但非唯一，数学教育还应让学生利用数学的眼光、思维、语言，利用从数学学习中积累的智慧应对未来的變化。也就是说，要把数学学习作为重要的载体，去培养学生一生受用的关键能力、必备品格、正确的价值观，发展学生的核心素养。这里的核心素养不应局限于数学核心素养，还有其他核心素养。核心素养的本质是会学习、会做事、会创造。未来没有固定答案，但当拥有思考力、学习力、实践力、创造力时，就拥有了适应、改造未来的普适性底层能力。所以，数学教育不应局限于数学学习，还应观照学生人生成长。“循源而学”提出的循成长逻辑而学、循适应未来而学便是对此的回应。

（三）回归人的完整与幸福生活：从数学教学走向数学育人

数学教育不仅应关注育智，也要关注育人，不仅要奠基未来幸福生活，也应观照当下学生的健康成长与幸福生活。数学源于生活，也服务于生活。离开生活的数学是无用的，抛弃生活的数学也是乏味的。数学学习的过程本身也是一个不断内化与外化、输出与应用的过程。所以小学数学教育要特别关注与生活的融通让学生学会用数学解决真实问题，激发学习数学的持久兴趣，关注学生积极向上生活态度的培养，关注学生效能感、成就感、幸福感等积极情感的累积。让他们通过有温度、有情感的数学学习活动，从小热爱生活、热爱生命、热爱世界，树立自信，期待未来；从小培养良好的习惯，涵养良好的品格，养成科学精神，助力完整的生命成长与幸福生活。“循源而学”也关注循完整与幸福生活的逻辑而学［3］。

综上，从数学学习走向人生成长，从人生成长走向完整且幸福的生活，是一切学科学习的基本“源”与“流”，是系列内化与外化、专与博、立己与达人、出发与归宿、基础与发展，是自然生长、生发、生态过程，是学科育人的“源”态。所以破解数学教育三大难题的关键在于厘清数学自身发展源流，循着学科发展之源、人生成长之源、生存生活之源而学习，从数学学习走向数学育人。

二、“循源而学”的理论结构

循源而学指循着本源、循着逻辑、循着通理、循着规律进行学习，进而看见数学、理解数学、学通数学、学好数学、用好数学、爱上数学。其理论结构的核心为“三循而学”。

（一）循数学发展之源而学

循数学发展之源而学就是循着数学产生与发展的逻辑而学。数学是研究数量关系与空间形式的科学。科学最显著的特征便是有成体系的知识。知识是人们在改造世界的实践中所获得的认识和经验的总和。认识是人脑对客观世界的反映。

数学知识就是人脑对客观世界中的事物从数学方面的属性进行反映，并通过改造，形成规范的符号或概念表达。数学知识何以产生和发展，就是要探析为什么人脑要反映与能反映。梳理数学知识的产生会发现，现实生活中，人们发现与提出了一些问题，如今天的羊是不是都回到了羊圈里。需要对羊从数量多少这一属性进行经验反映，数量多少可以数一数，后产生了数。数产生后，自然就要深入研究各种数有什么性质。数量与数量之间还会发生关系，两个数量之间的关系有大小、倍比关系等。数量还会发生变化，与其他数量合起来，就会得到一个新的数量。可以用加法运算来表示合起来的过程。计算出结果就产生了算式，表示合起来的过程与结果。算式不仅表示过程与结果，多个具体的算式抽象就成了部分量、部分量与合起来的数量的固定关系。算式从表达过程与结果走向表达数量关系。运用数量关系就可以解决生活中的问题。以此类推，产生减法、乘法、除法运算。这些新的知识又成为新的“经验”，助力学生反映与规范表达。可见“数数、数的意义与读写、数的性质、两个数量之间的关系、数量变化与运算、算式、多个数量之间的关系、解决问题”是所有学习数与运算主题内容时都要经历的认知过程。通过数学知识解决了数羊数量的问题，但随着生活的变化，又会产生新的问题。如此循环往复，数学知识则不断产生、关联、发展。

数学学习过程的本质就是数学产生与发展的复演。复演非完全像专家一样创造新知识，更多是习得已有数学知识。加之学生非“专家”，数学学习的过程则非纯粹的数学研究过程，需要学生具备一定的基础知识、基本技能、基本思想、基本活动（“四基”）经验，并具备一定的发现、提出、分析与解决问题能力，以此为主观反映提供经验基础。同时，还要不断累积兴趣、信心、科学精神、良好习惯，以便驱动下一次学习［4］。

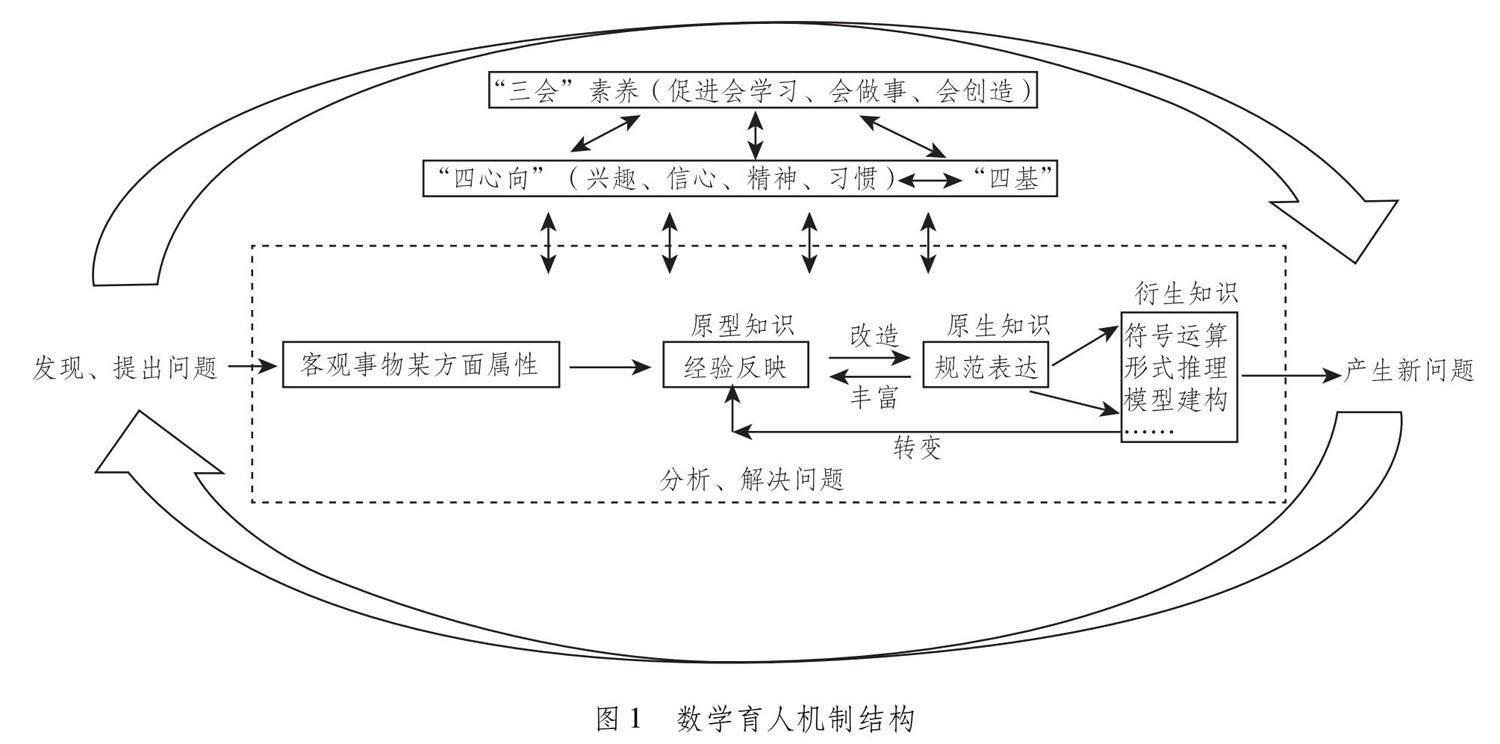
所以，数学学习的本源与逻辑、通理与规律是以问题发现、提出、分析与解决为主线，以知识学习为主载体，以“四心向”“四基”和“三会”素养为基础，推动问题解决与新问题产生，推动数学产生、发展与应用，在此过程中，又进一步获得“四基”，提升“四心向”，发展“三会”素养，循环往复，螺旋上升（详见图1）。

可见，数学学习重在丰富原型知识（经验型知识），构建原生知识（如“数”）与衍生知识（如乘法由加法变来）结构体系，不断累积“四心向”，获得“四基”，提升“四能”，这些发展又成为下一次新知学习的基础，如此螺旋上升，提升数学学习力。

（二）循人生成长之源而学

循数学发展之源而学能顺藤摸瓜，直抵数学本质，每一节课都让学生感受到数学知识是如何产生的、发展的、关联一体的，也能看到一类主题内在的一致性与认知结构。如此，学生便能看见数学、理解数学、学通数学。但若仅停留在“四心向”“四基”上，学生只是一个数学学习者，还未成为一个数学建构者、创造者，也未成为一个数学应用者、实践者，所以需要从关注会学数学拓展到更好成长上去。人生成长一方面需要关涉学生德智体美劳全面发展，另一方面也需要为学生未来奠基，也就是发展学生的核心素养，让他们从小会学习、会做事、会创造。首先，应看到“三会”素养既是学生学习数学的素养基础，也是学生学习数学后的结果与发展。如数感，在真实情境中理解数的意义，能用数表示物体的个数或事物的顺序；能在简单的真实情境中进行合理估算，作出合理判断；能初步体会并表达事物蕴含的简单数量规律。学生在学习整数时感受到数是对数量的抽象表达，数是多少个计数单位的表达。后面再学分数、小数、负数，学生就能基于初步形成的数感更好地理解它们的意义，然后又提升了数感的发展水平。其次，数学教育中，还要充分、适切、合理挖掘该知识载体是否还可以培养其他核心素养。如人教版三“毫米的认识”一课，可引用“英国1毫米航空事故”的素材，让学生感悟“差之毫厘失之千里”的精益求精的科学精神，同時培养学生的社会责任感。总之，要以数学学习为载体，发展学生的核心素养，从而感悟数学内在的一致性，感悟数学学习的通理通法，从小学会学习、学会做事、学会创造。

（三）循生存生活之源而学

数学育人是一个由内及外、立己达人，从基础到拓展的自然生长、生发、生态过程。一方面，数学源于生活，服务于生活；另一方面，学通数学，学好数学、最终是为了用好数学，过一种完整、健康、向上、富足、幸福的生活。生活既指当下的儿童生活，也指未来的成人生活。马克思认为，人的生存与生活本质是主体对自我、自然、社会与精神的系列价值的认识、改造与审美活动。由此，数学学习还应促进学生的完整生活、幸福生活，注重引导学生从小树立正确的世界观、人生观、价值观；数学学习还要让学生“亲自下田”去实践、去应用、去解决生活中的实际问题，去改造这个世界；数学学习还应让学生累积积极的生活情感与态度，热爱生活、热爱生命、热爱世界；数学学习还应适当渗透审美，让学生感受到数学的简洁美、对称美、一致美、严谨美、精确美等，感受数学眼光、数学思维、数学语言在生活中的广泛应用，感受数学与其他学科、文化、科技、生活的联系，进而感悟数学的价值。

综上，循数学发展之源而学旨在提升学习力，看见数学、理解数学、学通数学；循人生成长之源而学旨在知一识百、举一反三，会学习、会做事、会创造，学好数学，提升可迁移理解力；循生存生活之源而学则关注学生的完整生命成长与幸福生活，用好数学，感受数学的价值，进而爱上数学。“循”既是探寻、发现、遵循，也是数学教育的策略、原则与方法。第一，情境与问题是数学学习的驱动器与主线。第二，体验与实践（经验反映与规范表达的生活基础）是基本的学习方式，让学生在玩中学、做中学、用中学、创中学。第三，关联与综合是基本方法论，通过前后关联，唤醒原型知识、原生知识、衍生知识，打通知识之间的壁垒，自动沟通，形成结构化的认知体系，学通数学。通过综合，优化思维工具，丰富经验基础，将其他学科、文化、科技、生活的最新发展主动关涉、纳入、拿来，助力数学学习。第四，拓展与长程是数学学习的开放生态。在学习过程中，不要“闭关锁国”，而要“主动开放”，让学生自然地进行拓展学习（如数学文化、生活中的数学、联想同类前后相关主题的学习）与长程延学、深度学。第五，最后如何检测学生学习的效果，唯有通过系列创造与成长予以评测，同时创造与成长也是学习的结果与终极归宿。所以，“情境与问题、体验与实践、关联与综合、拓展与长程、创造与成长”是循源而学的五大设计与实施要义①（详见图2）。

三、“循源而学”的教学实践：以“比的认识”教学为例

比的认识重在理解比的意义。比的本源意义是表示同类量间的倍数关系，基于本源意义表示倍数关系，两个不同类量相比还衍生出了“产生新量”的“流”意义。本课重在溯本清源，厘清“源”与“流”的具象意义。其中“源”的意义是重点，“流”的意义是难点［5］。结合学情，将本课的教学目标确定如下：第一，理解比的意义，能正确读和写比，知道比各部分的名称，会求比值，理解比与除法、分数的关系;第二，经历从具体情境中抽象出比的过程，通过观察、思考，理解数学知识之间的联系，体会变与不变的数学思想;第三，能利用比的知识解释与解决一些简单的生活问题，感受比在生活中的广泛应用，进一步发展数感、符号意识与推理意识。下面基于循源而学的五大设计与实施要义，具体阐释本课的教学设计。

（一）情境与问题：驱动器与主线

学习首先要驱动学生行为参与、思维参与、情感参与，在具体情境中以大问题贯通，小问题串联的教学设计可以充分激发学生的探究欲，变“要我学”为“我要学”，促进深度学习发生。小学数学中常见的情境包括数学情境、生活情境、科技情境、社会情境等。常见的问题引出方式有提问、追问、反问、互问等。

本课始终以中华美食系列素材与大问题“比的意义”贯通，以系列小问题串联整个学习。如开课时，教师设置了中华美食文化源远流长的情境，请学生说一说自己喜欢吃哪些美食，迅速地拉近了师生距离，也引出了研究素材重庆小面，激发了学生的学习兴趣。

（二）体验与实践：学习方式

本课以自主探索性实践为主，先后设计了4个大的体验与实践环节：第一，通过和面，在变与不变中初步理解比的本源意义表示同类量之间的倍数关系；第二，对比国旗长宽之比与足球比分，在辨析中深化理解比的本源意义；第三，紧接着和面，引出吃小面，通过总价与数量、路程与时间的比，理解比的衍生意义，两个相关联的非同类量相比，产生新的量；第四，自学感悟比的抽象意义表示两个数相除。如：第一个环节，开篇教师提问，要做好一碗重庆小面，最重要的是什么？学生可能说是面。教师追问，让你来和面，面粉放多少克，水呢？学生随意列举，教师引出程师傅的经验——面粉200克，水100克。教师进一步追问，按程师傅的经验，面粉还可以放多少克，水呢？学生列举，发现可以简洁说成面粉是水的2倍或水是面粉的1/2，教师引导还可以用2 ∶ 1来表示。用比来表示数量间的倍数关系更简洁、更直观。这个过程让学生充分体验与实践，学生感受到面粉和水可以同向变化，但它们之间的倍数关系始终不变，2 ∶ 1是数量间倍数关系表征的又一次升级，进而建立清晰的比的意义的表象。

（三）关联与综合：方法论

关联指学习过程中要不断新旧沟通、前后联系、左右融汇，找到数学学习的通理、通法、通性，基于本质感悟数学内在的一致性；还指在学习新课后，要及时进行总结，建立清晰的认知结构，从而学通数学。综合则是主动沟通数学内部、数学与其他学科、数学与广域世界万事万物的关系，多开展跨学科主题学习，多应用其他学科、其他领域的知识、思想与方法帮助我们分析与解决问题，为数学学习提供参考与经验、智慧与营养，提升数学学习力。

本课在新课学习的第二个环节，对比国旗长宽之比与足球比分，在辨析中深化理解比的本源意义时，教师呈现视频足球比分变化的随机性，非呈倍数变化，借助这样的生活经验，学生立刻就明白足球比分表示的是两个队进球的具体个数，不是今天数学里所学的比。在第三个环节，紧接着和面，引出吃小面，通过总价与数量、路程与时间的比理解比的衍生意义。出示吃面情境，14元买2碗小面，让学生写比。学生基于同类量的比表示倍数关系，有的认为不能写成比，有的则认为可以，因为两个数量是同向变化，总价增加、数量也增加，但单价不变，具有倍数关系的特征，所以可以写成比。这就是利用刚学习的比表示倍数关系的特征——前后项具体数量可以变，但比值（倍数关系）始终不变，进行了类比迁移与推理。所以数学学习本质就是不断转化成旧知识进行理解，也就是关联已有经验与旧知识，综合各种经验与方法进行建构。

（四）拓展与长程：开放生态

拓展指横向的延伸，促进学生由此及彼、由点线及面体、由数学到生活（如生活中的数学）的思考，以此拓宽视野，活化知识。长程指在学习过程中，自然生成的由表及里（深究）、由当下到过去与未来（如数学文化与数学历史等）、由延学（生发的新问题、新主题学习）到长学（对该主题进行长程研究甚至终身研究）的学习样态，进而激发探究欲，打开数学学习场，涵养科学精神，感受数学的价值与魅力。不管是横向的拓展还是纵向的延伸，它们的共同点是学习进程中的自然延展、左右兼顾、承上启下，将一节课的学习自然打开。

在新课4个环节结束后，追问学生，比的意义简不简单，学生回答简单。教师顺势引出，数学家对比的研究不简单，出示比的研究历程的微视频，拓宽了学生的视野，厘清了比的产生发展历程，也激活了学生的民族自豪感，涵养了科学精神，从数学教学走向了数学育人，真正让课堂成为立德树人的主阵地、主渠道。

（五）创造与成长：结果、归宿与素养评测

创造的本质就是在继承中发展，并非无中生有。同样的创造也有很多层次，新知建构、练习应用、作品生成、发现新规律等都是创造。成长主要指核心素养的发展，集中表现为会学、会做、会创造、会生活。所以，创造与成长是广义上的学习结果、成长表现，也是一节课的目标指向，以及目标达成与否的重要评测指标。

本节课设置了3个层次的练习，最后让学生用自己喜欢的方式来总结这节课的所学、所思、所惑以及还存在的问题，就是通过问题驱动、任务完成、作品创造来检验学生学得怎么样，成长得如何。第一个练习紧接美食，请学生根据北京烤鸭中蛋白质、脂肪等含量一览表来写比，进一步内化比的意义，也让学生感受比的有序性。第二个练习是三杯蜂蜜水，可以通过比值来判断哪一杯最甜，巩固了比值的意义，感受比的度量价值。第三个练习让学生说一说生活中还在哪些地方见到過比，再出示“生活中的比”微视频，进一步感受比可以直观反映数量多少，具有度量价值，可以成为一种标准，以拓展比的应用价值，激发学生的延学探究。最后让学生通过自己喜欢的方式来表达自己的所学所思，本质上就是一种内化后的外化创造。

注釋：

①五大设计与实施要义：是本质概括、是目标导向、是原则遵循、是要素把握、是环节参考，其特点为由外及内与由表及里的深度学习、玩做用创结合的实践学习、文化生活泛在学习、前中后长程学习。

参考文献：

［1］教育部.义务教育数学课程标准（2022年版）［M］.北京：北京师范大学出版社，2022：1.

［2］李方红.互生教育理论刍论［J］.教学研究，2021（05）：20-25.

［3］李方红.融合教育生态下的学习变革：互生学习刍论［J］.教学研究，2022（06）：15-21.

［4］李方红.让数学化真正发生：“和真数学”教学理念与实践探索［J］.现代教育科学，2019（11）：86-92.

［5］李方红，党心池.“比的认识”教学实录与评析［J］.小学数学教育，2023（17）：44-46.

（责任编辑：姜佳宏）

Primary School Mathematics Teaching from the Perspective of

“Learning from the Source” Theory：Seeing Mathematics， Understanding Mathematics，

Mastering Mathematics and Making Good Use of Mathematics

LI Fanghong

（Bashu Primary School in Chongqing City， Chongqing 400013，China）

Abstract：   How to enhance the interest of primary school students in learning mathematics， enhance their mathematical learning ability， and appreciate the value of mathematics are the three major unresolved problems in current primary school mathematics education. The solution lies in letting students see mathematics， understand mathematics， master mathematics， learn mathematics well， make good use of mathematics， and fall in love with mathematics. The concept of “learning from the source” has emerged. It advocates learning along the “source” and “flow” of mathematics's emergence， development， and application， the core cotent includa learning from the source of mathematical development， learning from the source of personal growth， and learning from the source of survival and life. The concept of “learning by following the three principles” reflects the transition from mathematical learning to personal growth， and from personal growth to a complete life. This is the fundamental “source” and “flow” of all subject learning， and it is a natural growth， development， and ecological process that involves a series of internalization and externalization， specialization and erudition， self-improvement and mastery， starting and destination， foundation and development. The five design and implementation principles of “learning from the source” are “context and problems， experience and practice， correlation and synthesis， expansion and long-term development， and creation and growth”.

Key words：   learn from the source; seeing mathematics; understand mathematics; learn to master mathematics; make good use of mathematics