戴维孙-革末电子衍射实验数据的一点启示

2024-05-30苑新喜

科技创新与应用 2024年15期

关键词：电子

作者简介：苑新喜（1968-），男，硕士，副教授。研究方向為电子场与引力场。

DOI：10.19981/j.CN23-1581/G3.2024.15.020

摘要：1927年戴维孙（C. Davisson）和革末（L. H. Germer）的电子衍射实验第一次可争辩地验证实物粒子的波动性。事实上，与德布罗意（de Broglie）假设的理论计算相比，戴维孙-革末的电子衍射实验数据存在着一种明显的系统性偏离。在近百年之后的今天，该偏离或许为当前电子的电磁质量的研究提供一个有价值的启示和实验依据。

关键词：戴维孙-革末实验；电子衍射；电子；电磁质量；实验数据

中图分类号：O412 文献标志码：A 文章编号：2095-2945（2024）15-0092-04

Abstract： In 1927， the electron diffraction experiments of C. Davisson and L. H. Germer were the first to indisputably verify the fluctuation of physical particles. In fact， compared with the theoretical calculation of de Broglie hypothesis， there is an obvious systematic deviation in Davidson-Germer's electron diffraction experimental data. Nearly a hundred years later， this deviation may provide a valuable inspiration and experimental basis for the current study of the electromagnetic mass of electrons.

Keywords： Davidson-Gemer experiment; electron diffraction; electron; electromagnetic mass; experimental data

1924年，年轻的法国物理学家德布罗意受光的波粒二象性启发，在没有任何直接证据的情况下大胆地提出了一个假设：实物粒子也具有波动性[1-3]。同时，他把光子的动量-波长的关系公式也推广到实物粒子上，即λ=h/p，其中p是粒子的动量，h是普朗克常数，而λ就是实物粒子的波动性所对应的波长。由此，德布罗意开启了量子理论研究的新篇章。后来，德布罗意假设阐释的波称为物质波。

一开始，德布罗意自己就提出可以用晶体做电子的衍射来验证物质波的存在。虽然当时电子束技术已经在实验室里得到普遍的运用，但是直到1927年，戴维孙和革末[4-5]才通过电子束在镍单晶的晶体表面上的散射观测到电子的衍射现象，第一个证实了电子的波动性。同年，汤姆孙[6-7]拍摄到电子束穿过多晶薄膜时形成的衍射图样，再次证实了电子的波动性。德布罗意因实物粒子波动性的假设而获得了1929年的诺贝尔物理学奖，戴维孙和汤姆孙因证实电子波动性的实验而共同获得了1937年的诺贝尔物理学奖。

但是，应该看到，无论戴维孙和革末的实验数据还是汤姆孙的实验数据虽然都无可争辩地证实了电子的波动性，但是都存在一个共性问题，即实验数据都显示出一定的系统性倾向或偏向。戴维孙和革末明确指出其实验数据明显地存在一种系统性的偏离，并简单地将之归因于实验仪器的使用调节问题或结构设计的缺陷问题[4]。汤姆孙更是直言自己的实验测量数值比期望值都偏小至少4%，并明确提出这可能源于实验系统误差或 “一种未知的理论原因[7]”。由于缺乏详尽的汤姆孙实验的细节和数据，无法对其做进一步分析，本文只限于讨论戴维孙和革末的实验数据。

1 电子波长的得出

波长是描述波动性的最基本和最重要的特征物理量。在戴维孙-革末实验中，电子的物质波波长数值可由2种方式得到。

第一种方式是由德布罗意波长公式？姿=h/p得出。电子的动量p=m？淄，m是电子的质量，？淄是电子的运动速度。戴维孙-革末实验中电子束的加速电压V不超过370 V，这时电子的速度远远小于光速，电子运动的相对论效应忽略不计，取电子质量m为电子的静质量m0=9.11×10-31 kg。加速后电子的动能m？淄2/2等于电子加速时获得的电势能eV，e是电子的电量。由此推得电子的波长？姿=（h２/２em）■/V■。进一步，若波长公式中加速电压V的数值以伏特为单位计，将h、e和m这些常数的数值（国际单位制）代入公式，整理后波长公式简化为？姿=150■/V■×10■cm，由此得到电子的物质波波长？姿与电子的加速电压V之间的一个简明的关系式

即在理论上，电子的波长？姿与加速电压V的平方根的倒数是一个线性关系。（？魡是波长的单位符号，中文以汉字“埃”表示，1埃等于10-10 m。）

第二种方式是由晶体衍射公式dsin？兹=n？姿，即？姿=d sin？兹/n得出。d是晶体的晶格参数，是与电子运动无关的独立常数；？兹是衍射角，表示衍射条纹或衍射强度极值在空间的角度位置；n是衍射条纹或衍射强度极值的级次，在戴维孙-革末实验中n一般等于1，少数情况下n等于2。这种方式就是由实验中所观测到的？兹的数值确定相应的？姿的数值。

对比以上2种获得电子物质波波长的方式，不妨将第一种方式得出的电子波长的数值称为理论数值，将第二种方式得出的波长的数值称为实验数值。这2种方式实际上也是2种独立的获知电子波长的途径。这2种途径获得的波长数值是否相符，就成为戴维孙-革末实验成败的关键。

2 戴维孙-革末实验的数据分析

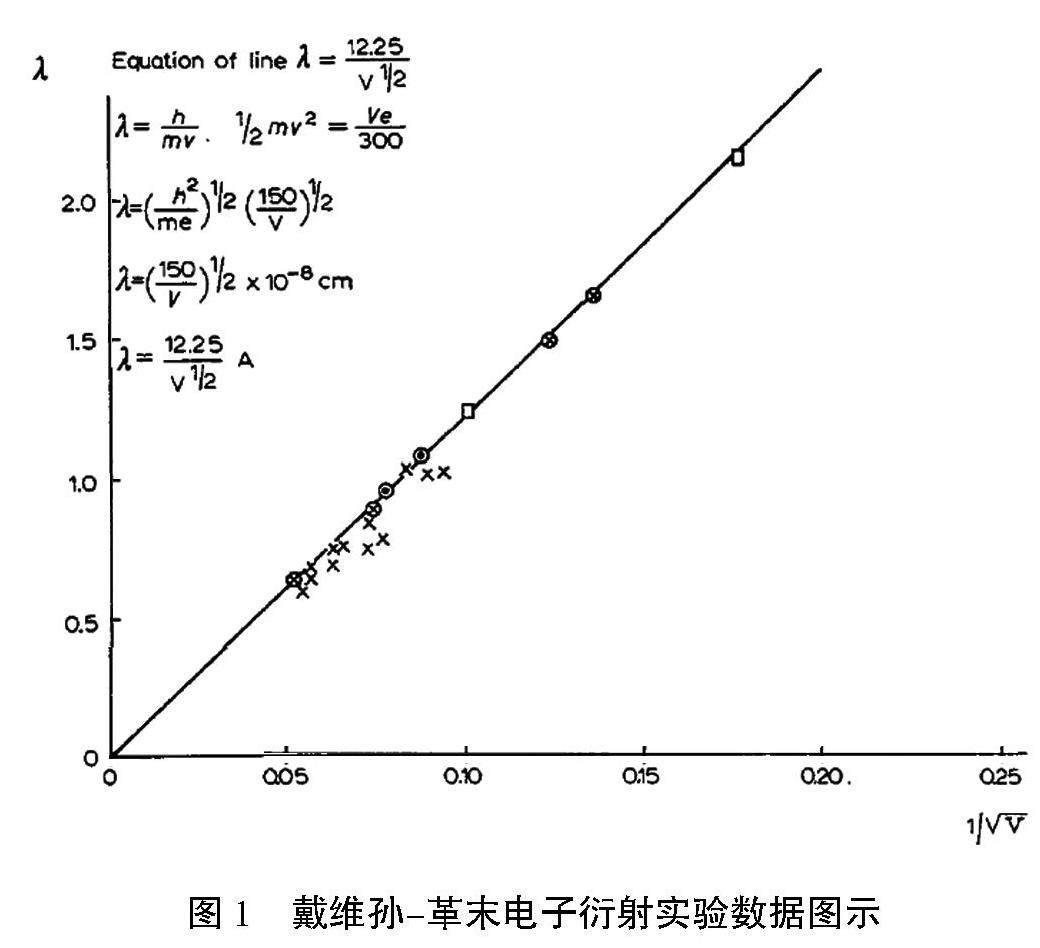
德布羅意假设提出以后，就有人开始尝试用晶体做电子的衍射实验，但都没有成功。戴维孙-革末实验的成功带有一定的偶然性。早在1921年，戴维孙就开始了晶体对电子束的散射实验研究。1925年春，戴维孙和革末用金属镍做电子束的散射实验时，出现了一次真空破坏事故，导致镍表面被氧化，为了还原，他们对镍作了加热处理，结果镍形成了单晶结构。重新开始实验后，发现实验现象和事故之前相比发生很大的变化，在某些方向上电子的散射强度变得异常偏大。这个新发现一时让他们感到很困惑，并没有认识到这就是电子的衍射现象。第二年，戴维孙到英国伦敦参加学术会议时听说了德布罗意假设，才得知其新发现可能就是电子物质波的衍射现象。回去后，戴维孙和革末有目的地对镍单晶的电子束散射做了更精确的实验测量，经过近半年的努力最终证实了电子的波动性。戴维孙-革末电子衍射实验的数据结果可以用图1予以全面显示。

图1引用自文献[8]，文献[8]是1937年戴维孙获诺贝尔物理学奖时的讲演文稿。戴维孙用图1总结性地展示了1927年他们先后公开发表的实验数据，非常直观地表现出了实验数据及其内部关系。为了增加信息的可信性，这里原文复制，没作任何改动。

图1 戴维孙-革末电子衍射实验数据图示

图1中纵坐标为波长？姿，横坐标为加速电压的平方根的倒数1/■。图1中的斜线对应波长公式？姿=12.25/V1/2，相当于是一条理论直线。图1中每个十字叉就是一个实验数据点，点的坐标值对应一组实验测量数据，横坐标是由衍射公式得出的波长？姿的实验数值，而纵坐标平方的倒数就是发生该衍射时实际上的加速电压。加了圆圈的十字叉表示它是一个非常可信和可靠的实验数据点（比如从右边数起的第二个和第三个数据点）。图1中2个小方框（从右边数起的第一个和第四个数据点）和2个带圆圈的圆点表示其他性质的实验数据，不在本文的讨论范围，本文从略。在图1的左上方戴维孙还特意说明了波长公式？姿=12.25/V1/2的由来。

首先，从图1可以看出，所有实验数据点都非常贴近理论直线，这意味着戴维孙-革末实验中电子物质波波长的理论数值与实验数值高度相符，为电子的波动性提供了强有力的依据。

其次，从图1可以看出，戴维孙-革末实验的数据结果存在着一种明显的系统性偏离，即实验数据点都在理论直线之下，这意味着电子波长的实验数值普遍小于其理论数值。再来看2组具体的实验数据。

在戴维孙-革末实验中，当加速电压V达到54 V时，在衍射角50°方向上观测了一级（n=1）衍射强度极值。这组数据在戴维孙-革末实验中占有特殊地位，不仅被认为是一组极为可靠的实验数据，而且作为代表性的实验数据专门予以重点说明，并反复出现在戴维孙自己撰写的3份实验报告文献中[4-5，8]，也是后来被各种物理教材广泛引用的一组实验数据[1-2]。加速电压V=54 V时，得出电子波长的理论数值是1.67埃[1-2]；再根据晶体衍射数据，晶格参数d为2.15埃，由衍射角？兹=50°得出电子波长的实验数值是1.65埃[1-2]。这组实验数据表明电子波长的实验数值略微小于理论数值。

在戴维孙-革末实验中另外一组较为典型的实验数据是当加速电压V达到65 V时，在衍射角44°方向上观测到了一级（n=1）衍射强度极值。从这组实验数据得出相应的电子波长的理论数值是1.52埃，实验数值是1.49埃，同样实验数值略微小于理论数值。

这2组实验数据在图1上对应着从右边开始的第二个和第三个数据点。这2个实验数据点尚且如此，其他的实验数据点更是表明电子波长的实验数值明显小于理论数值。

戴维孙和革末将这个系统性的偏离归因于实验系统误差，即由实验仪器的调节或设计引起。但是，正如汤姆孙所言，这种偏离也可能出于“一种未知的理论原因”，尝试给这个偏离提供一个理论上的原因。

3 对电子电磁质量研究的启示

戴维孙-革末的实验数据与德布罗意的理论假设高度契合，促使了人们对电子波动性的广泛认同，极大地推动了量子力学的发展，时至今日量子力学已成为认识微观世界的理论基础。或许正因为如此，长期以来人们无意中忽视了戴维孙-革末的实验数据所呈现出系统性的偏离。现在认识到，这个偏离可能在理论上关联着电子的电磁质量。

电子带有一个基本元电荷，这个元电荷所激发的电磁场就是电子自身的固有电磁场。根据爱因斯坦的质量能量关系（即著名的E=mc2），电子这个固有电磁场的能量对应着一定的质量，其称为电子的电磁质量。通常认为，电子的质量至少由非电磁起源质量和源自于电磁场能量的电磁质量这2部分组成。

自从120多年前J. J. 汤姆孙（前文汤姆孙的父亲）发现电子以来，人们曾经做出过各种各样的理论探索电子的电磁质量及电子的质量构成等问题，如彭加勒张力张量理论（Poincare Stress），再如波恩-英菲尔德的非线性电动力学理论和狄拉克等人提出的超前势理论，等等。由于缺乏实验依据等原因，这些努力最终都没能成功。电子的电磁质量至今仍是物理学中一个悬而未决的基础问题[9-13]。

打破以往的思维定势[9]，提出了电子电磁质量的一个新的研究思路，即电子的电磁质量不是电子已知的静质量m0=9.11×10-31 kg的组成部分，m0只对应着电子的非电磁起源质量。因此，电子的质量me是m0再加上另外的电磁质量mEM0构成，即me=m0+mEM0。

上述研究新思路不是完全孤立的一点认识，是引力的研究理论[14]中一个重要的逻辑推论，属于一系列关联逻辑中的一个环节，而且现在已找到了一系列的实验和理论依据。这些实验和理论依据除文献[15-16]外均已在文献[9-12]中一一列出，此不赘述。文献[10]、[11]和[13]正是基于这些依据对电子的电磁质量给出了一个定量参考结果，即电子的电磁质量mEM0与其已知的静质量m0比值在5%左右。

按照该研究思路，戴维孙-革末实验中电子波长的理论数值就必须作一点改动，即电子德布罗意波长理论公式？姿=（h2/2em）1/2V1/2中的电子质量m不再仅仅是m0=9.11×10-31 kg，而是把电磁质量mEM0的贡献也包含进去，即将波长公式中的m改为（m0+5mEM0/3），详细的推导过程从略[12，17]。以mEM0=m0×5%计，电子波长的理论数值在整体略微变小一点，图1中间的理论直线将往下稍微倾斜一点，部分数据点就落了在直线的上部，实验数据点相对于理论直线的分布形态更加趋于合理。这种改动对戴维孙-革末实验的结论没有任何影响。

反之，按照电子电磁质量研究的新思路，利用图1通过简单的作图法粗略推断，mEM0与m0的比值约为9%。对研究者而言，这个比值完全处于一个可接受的合理范围内，已经有了很高的参考价值。

综上所述，电子的电磁质量与其已知的静质量比值有可能在5%左右。这实际上意味着戴维孙-革末实验为电子的电磁质量研究提供了一个意义鲜明的实验依据。

4 对戴维孙-革末实验的一点想法

虽然戴维孙-革末的实验数据出现系统性的偏离，但是必须承认近一百年前的戴维孙-革末实验无可争辩地证实了电子的波动性。同时，或许局限于当时的技术条件，戴维孙-革末实验仍然存在着一些缺憾。戴维孙-革末实验的加速电压在30～370 V之间，最终也只在少数加速电压上观测到了衍射现象。如果能在其中任何一个加速电压上都观测到衍射现象，那就显得更完美。进一步，既然加速电压在54 V有显著衍射现象，如果在50～60 V的区间内，加速电压每增加0.5 V能持续而稳定地观测衍射现象，这样的实验结果最具说服力。反之，如果做不到这一点，就值得探究其中的原因。希望以后有研究者在条件许可的情况下，能充分利用现代先进的实验科学技术，弥补这些缺憾。同时，也可以为电子的电磁质量研究提供更可靠的实验数据。

这里不是单纯地追求单一实验的完美，只是研究者相信，无论电子自身还是原子核外的电磁场及其电子运动都存在着很多今天未知的奥秘，或许可以通过深入而广泛的晶体对电子束的散射、反射和衍射实验揭示这些奥秘。试想，如果没有先前多年的实验经验与认识的积累，戴维孙和革末不可能第一个证实电子的波动性。从这个角度看，戴维孙和革末实验的成功具有一定的必然性。

5 结论

电子电磁质量研究的新思路促使研究者关注和分析了近一百年前戴维孙-革末电子衍射实验数据。对戴维孙-革末实验数据的系统性偏离给出了一个理论原因，认为它关联着电子的电磁质量，并根据这些实验数据，推断出电子的电磁质量与其已知静质量的比值有可能在5%左右。这是继Bertozzi实验、康普顿效应和电子对湮灭实验之后，为电子的电磁质量研究提供的又一个意义鲜明的实验依据。

参考文献：

[1] 张三慧.大学物理学（C7版下册）[M].北京：清华大学出版社，2015：341-342.

[2] 杨福家.原子物理学[M].5版.北京：高等教育出版社，2019：71-72.

[3] 周世勋.量子力学教程[M].2版.北京：高等教育出版社，2009：7-8.

[4] DAVISSON C， GERMER L H. The Scattering of Electrons by a single crystal of nickel [J]. Nature，1927（119）：558.

[5] DAVISSON C， GERMER L H. Diffraction of Electrons by a crystal of nickel[J].Physics Review，1927（30）：705.

[6] THOMSON G P. Diffraction of cathode rays by a thin film[J]. Nature，1927（119）：890.

[7] THOMSON G P. The Diffraction of Cathode Rays by Thin Films of Platinum [J].Nature，1927（120）：802.

[8] DAVISSON C J. The discovery of electron waves[J]. The Bell System Technical Journal，1938，17（3）：475.

[9] 苑新喜．关于电子电磁质量问题的一点探讨[J]．甘肃科技纵横，2016，45（11）：70-74.

[10] 苑新喜．应用康普顿散射研究电子的电磁质量[J]．甘肃科技纵横，2015，44（5）：39-41，66.

[11] 苑新喜．应用Bertozzi实验研究电子的电磁质量[J]．实验科學与技术，2016，14（2）：4-7.