45 m超高堆垛机立柱结构设计与仿真验证*

2024-05-29章真雄龙海强

起重运输机械 2024年8期

章真雄龙海强

苏州迈卡格自动化设备有限公司苏州 215163

0 引言

近年来，我国经济高速发展，商品流通和仓储需求急剧增加，更促进了物流仓储行业的快速发展，对仓储效率、智能化程度的要求也日益提升。自动化立体仓库在现代物流仓储行业中发挥了巨大的作用，它能加速商品流通，减少商品损坏，降低流通成本，节约土地面积、人力和财力[1-3]。其中，智能巷道堆垛装备是现代自动化立体仓储建设和运行的关键设备之一，其性能是影响自动化立体仓库效率的重要因素[4]。工业发达国家的物流堆垛装备技术非常先进和成熟，基本实现了规格化和标准化。与工业发达国家相比，虽然我国物流设备技术发展很快，但仍有较大差距，特别是在标准化、系列化、规格化、理论计算和设计制造等方面尤其突出[5-7]。当前国内智能巷道堆垛装备的运行速度一般为160 m/min，高度在30 m以下；而国外智能巷道堆垛装备运行速度可达240 m/min，高度最大可达45 m[8，9]。超高智能堆垛装备研发将极大地提高立体仓库的库容量，大幅提高土地的利用效率，已成为我国智能化物流仓储业发展的必然要求。

目前，超高智能巷道堆垛装备主要采用单立柱结构形式，单立柱堆垛装备的优点是结构简单、横向尺寸紧凑、巷道占宽小、围绕立柱可选用多种载货台等，其缺点是立柱受力情况复杂、结构设计校核困难，故其产品开发的关键是必须保证立柱结构和下横梁结构具有足够的强度、刚度和稳定性[10-12]。单立住巷道堆垛机为复杂空间薄壁壳体与实体结构的混合体，由于结构及受力状态的复杂性，通常采用有限元方法对堆垛机主要金属结构进行受力分析和关键特性评价[13]。然而，有限元法在堆垛机主体结构布局设计阶段却因没有几何数据而难以实施，为此探索堆垛机设计简化计算方法，并结合工程化数据，用有限元仿真验证简化计算方法的有效性对提高超高堆垛结构设计的效率具有重要的指导意义。

1 45 m超高堆垛机立柱设计

如图1所示，典型的堆垛机简化结构主要包括下横梁、立柱和载货台3部分，其中立柱是堆垛机结构的重要组成，也是堆垛机性能指标保证的基础。

图1 堆垛机受力图

1.1 堆垛机立柱截面设计

堆垛机立柱刚度是组成堆垛机结构静态刚性的主要参数。JB/T 7016—2017《巷道堆垛起重机》要求静刚性设计变形量不大于Hh/1 500。欧洲机械搬运协会则有更苛刻的设计要求，本文参照FEM9.831的相关要求，立柱顶部变形ymax不大于5 mm。

在静载作用下，立柱受到自身质量Pm、载货台载质量Pf和荷载质量Ph等载荷作用。由分析可知，载荷台质量及质心偏距是引起立柱弯曲变形的主要因素。常见堆垛机立柱结构设计可以简化为典型悬臂梁结构，由此计算立柱弯矩变形的公式为

式中：E为材料弹性模量，E＝210 GPa；I为立柱截面在Z轴上的惯性矩；M为载荷台质量及质心偏距作用于立柱的弯矩；L为立柱高度。

根据该型堆垛机开发要求，货叉质量Pf＝300 kg，最大荷载质量Ph＝1 500 kg，立柱最大立柱高度H＝45 m，货台及载荷质心距离立柱前端表面距离Ls＝1.2 m，立柱最大Y向挠度ymax＝0.005 m。由此，计算作用于立柱力矩M为

由式（1）可计算得到立柱截面Z轴的惯性矩，即

将上述参数代入式（3）可得IZ-M＝0.020 412 m4，由此立柱截面惯性矩设计值应大于0.020 412 m4的要求。如图2所示，该立柱截面采用40C槽钢与钢板拼焊成箱形梁结构。经设计选型计算，该立柱截面在Z轴上的惯性矩为IZ-M＝0.024 515 m4；在X轴上的惯性矩为IX-M＝0.001 76 m4，大于设立柱刚性设计惯性矩的基本要求。基于该堆垛机立柱断面设计，可得立柱截面面积As＝0.047 4 m2；结合钢材密度和截面尺寸可得每米立柱质量为372 kg，立柱总质量Pm＝16 740 kg。由图2可得，立柱截面形心在Z向到截面最远边缘的距离eZ-M＝0.245 m；在X向到截面最远边缘的距离eX-M＝1.180 m。

图2 立柱截面轮廓设计

1.2 堆垛机立柱静应力估算

在堆垛机立柱组件质量Pm、货叉质量Pf、荷载质量Ph和偏载弯矩ML、载荷台质量Ps和载荷台弯矩Ms共同作用下，堆垛机立柱底部结构应力状态主要表现为前侧面表面具有最大压缩应力状态，后侧面表面具有最大拉伸应力状态。偏载弯矩和载荷台弯矩计算分别为

其中，Lh＝1.2 m，Ls＝0.3 m，eX-M＝1.18 m，Ps＝530 kg。分别代入式（4）、式（5）即可得到ML＝36 515 N·m，MS＝6 077 N·m。

应用经典材料力学计算方法，计算立柱结构底部前侧表面（槽钢侧）最大压缩应力σ3及后侧表面（盖板侧）最大压缩应力σ1，表达式分别为

式中：Am为立柱截面积。

将上述参数分别代入式（6）和式（7）可得最大拉压应力为σ3＝-5.99 MPa，最大拉应力为σ1＝-2.43 MPa。立柱设计材料选型为Q235，其屈服强度为235 MPa，立柱静载荷应力估算结果满足设计材料强度要求。

1.3 立柱结构固有频率计算

依据经典振动理论[14]中关于杆梁固有频率的计算公式，以载货台及荷载处于立柱顶端位置为立柱结构固有振动频率的计算工况。此时，可将载货台及荷载全部等效于悬臂梁上端点质量m，立柱结构可等效为无重弹性悬臂梁的均布质量ms，不考虑重力荷载的影响，参照杆端有集中质量的振动（见图3）进行固有频率的计算。

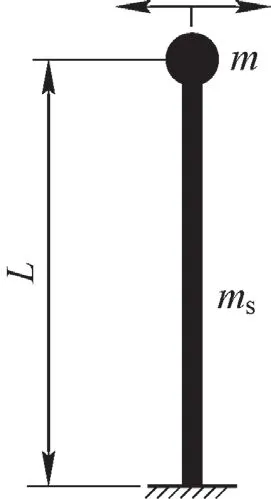
图3 杆端有集中质量的振动

立柱结构沿X向即运行方向的振动为横向振动，其第1阶固有弯曲振动频率为

将L＝45 m、IZ＝0.024515 m4、E＝210 GPa、集中质量m＝Pf+Ph+Ps=2 330 kg、均布质量ms＝16 740 kg等立柱简化结构的相关参数，带入式中，计算得到堆垛机立柱简化结构沿X方向第1阶弯曲振动固有频率为0.83 Hz。

2 堆垛机立柱设计仿真验证

基于材料力学经典公式和基本受力分析，可以用于堆垛机立柱截面正向设计估算，但难以解决立柱结构详细应力分布问题。有限元方法和各种专业仿真软件的出现和发展为复杂结构应力分布和强度评价等提供了便利，也是当前各类产业设计开发常用的仿真验证方法。

2.1 堆垛机立柱有限建模

Hyperworks是一套杰出的CAE仿真平台解决方案，它整合了一系列仿真工具，包括建模、分析求解器、优化、可视化、流程自动化和数据管理等解决方案，广泛应用于机械设计制造、汽车工业等行业的仿真优化，提供了出色的基础静力学分析、动力学分析、结构振动分析、优化设计等多学科领域[15-17]。

在堆垛机结构的有限元建模中，对堆垛机下横梁结构、立柱结构和载货台结构进行3D精确尺寸建模，对驱动电动机、电控柜、操作平台和维修平台等辅助子部件进行去除简化（因这类部件结构对整体的强度和刚度没有加强作用），并能减少模型的数据量，加快主要结构的数据分析。在Hypermesh建模环境设置立柱等钣金主体结构有限元网格，最小单元尺寸为20 mm，采用Shell单元快速生成立柱、下横梁等钣金结构网格模型。货台结构采用Solid单元建立有限元模型，焊缝位置采用共节点方式建模，堆垛机系统主体结构模型共有750 591个节点，744 071个单元。其中，立柱及货台、立柱及下横梁等结构有限元模型分别如图4所示。

图4 立柱、货台及下横梁有限元模型

2.2 堆垛机立柱静载仿真验证

当堆垛机载荷台位于立柱顶部时，货叉伸出状态明显影响结构偏距载荷，故立柱结构有限元静应力分析分别选取货叉的2种极限位置工况进行性仿真分析。

当货叉为不伸出状态时，堆垛机立柱顶部最大位移为10.01 mm，如图5a所示。最大位移位于立柱顶部载荷台，其局部位移云图及位移极值点放大图如图5b所示。仿真分析不仅预测了立柱顶部位移情况，同时也发展立柱下横梁弯曲变形的位移值为0.97 mm，如图5c所示。由于立柱长度达到了45 m，故下横梁弯曲变形将明显影响顶部位移值。进一步分析载货台位于立柱底部，获得立柱顶部最大位移偏转为5.13 mm，则立柱顶端相对位移满足5 mm要求。

图5 货叉不伸出位移云图

如图6所示，货叉不伸出状态时立柱底部前侧表面（槽钢侧）的最大应力为96.94 MPa，盖板侧最大应力为62.86 MPa；立柱下横梁上表面的最大应力为68.02 MPa，下横梁腹面最大应力为59.98 MPa，位于滚轮安装孔区域。

图6 货叉不伸出应力云图

当载货台位于立柱顶部且货叉伸出时，载货台框架的水平横梁同时受到在XOY平面和YOZ平面的双向载荷弯矩作用。此时，载货台处于最不利的工作状态，其结构强度性能是重点考查指标。货叉伸出与不伸出时载货台水平横梁结构应力分布云图对比如图7所示，货叉伸出时载货台水平横梁结构的应力为53.91 MPa，货叉不伸出时载货台水平横梁结构的应力为26.50 MPa。由货叉的2个状态对比分析可知，货叉伸出状态对载货台结构受力和应力分布影响明显。在堆垛机产品开发应用中，应重视考查货叉伸出状态的结构受力分析和强度校核，特别是双伸货叉结构设计，因其外伸行程是单伸货叉行程的2倍左右，在YOZ平面内的载荷弯矩增加明显。

图7 货叉伸出状态应力云图

2.3 堆垛机模态仿真验证

机械结构的固有频率和模态振型特性决定了其在不同动态载荷和外界激烈下的响应。了解结构的固有频率和模态振型有助于防止机械结构会因共振引起的问题，模态振型也可评估共振激励引发的结构过度变形问题。

结合45 m超高堆垛机立柱经典杆梁模型计算边界和质量配置，建立该堆垛机立柱和载荷台模型进行模态分析。模型质量为18 940 kg，仿真分析结果显示，当载货台及荷载处于立柱顶部时，堆垛机第1阶整体模态为1.05 Hz，模态振型表现为绕立柱底部沿X向的整体弯曲模态，如图8a所示。堆垛机立柱第2阶模态频率为1.77 Hz，模态振型表现为立柱绕运动方向转到，如图8b所示。本文在堆垛机立柱早期设计阶段，采用杆端有集中质量的振动的频率计算公式，得到堆垛机立柱简化结构沿X方向第1阶弯曲振动固有频率为0.83 Hz，这表明简化计算结果在前期设计中有一定参考性。

图8 立柱模态与振型

堆垛机主体结构约束模态性能是考虑载货台、立柱、下横梁等整体结构性能。由于载货台在立柱上的位置对立柱模态频率和振型都有影响，本文选取货台位于立柱顶部、中间和底部3个位置进行分析，下横梁的分析模型总质量为20 675 kg。对应货台不同位置分别提取立柱前5阶模态进行统计对比如表1所示。

表1 载货台位置对应堆垛机固有频率对比 Hz

经过分析可知，在加装下横梁结构后，堆垛机整体结构一阶模态频率为0.832 Hz，模态振型为立柱弯曲变形，与简化理论计算结果很接近。当载货台位于立柱顶部时，立柱固有频率最低，且较载荷台位于中间位置时频率降低了23.8%。立柱第1阶模态振型表现为顶部沿X方向偏转，该指标是评价立柱刚性的重要参数，故立柱设计开发时应重点控制载荷顶部位置变形量。

2.4 堆垛机动态载荷仿真验证

当堆垛机沿X向轨道运行时，典型工况有加减速、匀速运行、紧急制动和碰撞缓冲器等，其中匀速运行状态和静止状态受载荷情况一致。堆垛机动态载荷工况仿真选取受载最苛刻的载货台处于立柱顶部状态进行。

堆垛机在不同工况下，惯性加速度系数取值不一样。在等效平衡力系中，对堆垛机各部件施加惯性力，其中载货台及荷载，下横梁等施加集中惯性力，立柱结构由于高度比较长，施加均布惯性力，堆垛机的惯性力系加载如图9所示。结合堆垛机运行常用的加速、制动、碰撞等3个典型动态载荷工况惯性载荷系数，分别计算得到各部分惯性载荷如表2所示。

表2 典型工况下的惯性力 N

图9 堆垛机立柱惯性力

在仿真环境完成模型约束和加载工况设置并计算得到各工况应力分布。以制动分析结果为例，当堆垛机在正常运行过程中以加速度a＝0.5 m/s2向前运行制动时，立柱底部最大应力为77.7 MPa，其应力云图如图10所示。

图10 制动工况底部应力分布

分别将加速、制动和碰撞这3个惯性载荷工况分析的Mises应力和位移量统计对比，如表3所示。对比结果显示，在碰撞缓冲器时，结构受到的减加速度影响很大，是一种比较危险的状态。碰撞缓冲器工况立柱底部的Mises应力值增加较大，最大达到194.3 MPa。进一步分析各组件最大拉伸应力状态可知，碰撞工况下的最大拉伸应力为131.8 MPa，位于40C槽钢与下横梁的上表面焊接位置；下横梁上表面的最大拉应力为105.3 MPa。拉伸应力是导致结构强度失效的关键因素，碰撞工况堆垛机结构的最大拉伸应力为131.8 MPa，明显小于材料Q235的屈服极限下限值235 MPa。这表明堆垛机结构强度具有足够的安全余量，而堆垛机刚性参数则是立柱系统开发的重点。