例谈选函数图像常用的方法

公衍录

选择符合题意的函数图像一直是高考考查的热点问题之一，下面结合实例介绍选函数图像常用的几种方法，供同学们参考。

一、根据函数表达式选择函数图像

先根据题意和物理规律，推导出图像纵、横坐标轴代表的物理量满足的关系式———函数表达式，再依据“函数表达式与函数图像相对应”选出符合题意的图像。例如，若函数表达式形如y=kx+b，则对应的函数图像为直线;若函数表达式形如y=ax2+bx+c（a≠0），则对应的函数图像为抛物线。

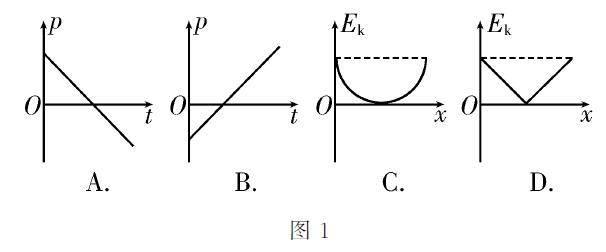
例1 在t=0时刻，将一物体（可视为质点）竖直向上抛出，忽略空气阻力。以抛出点为坐标原点、竖直向上为正方向，如图1所示的四个选项中能正确反映该物体的动量p随时间t 变化、动能Ek 随位移x 变化的图像是（ ）。

解析：设物体的初速度为v0，则t 时刻物体的速度v=v0-gt，动量p=mv，解得p=mv0-mgt，因此物体的动量p 与时间t 是一次函数关系，对应的函数图像是一条直线，且直线的斜率k=-mg，选项A 正确，B错误。根据速度与位移的关系式v2-v20=-2gx，动能Ek=1/2mv2，解得Ek=1/2mv20-mgx，因此物体的动能Ek 与位移x 是一次函数关系，对应的函数图像是一条直线，且直线的斜率k=-mg，选项C、D错误。

答案：A

例2 滑沙是人们喜爱的一项游乐活动。如图2所示为滑沙场地的一段，人和滑车从斜面顶端A 点由静止下滑，斜面的倾角为θ，取沿斜面向下为正方向，如图3所示的四个选项分别是人和滑车沿斜面向下运动过程中的加速度a 与时间t、速度v 与位移x、重力的瞬时功率P重与时间t、动能Ek 与位移x 的关系图像，其中正确的是（ ）。

解析：选由人和滑车组成的整体为研究对象，在整体沿斜面下滑的过程中，根据牛顿第二定律得mgsin θ-f =ma，解得a =gsin θ-f/m ，因此a-t 图像是一条平行于t 轴的直线，选项A 错误。根据速度与位移的关系式v2=2ax，解得v=根号下2ax ，因此v-x 图像是一条过原点且开口向右的抛物线的一部分，选项B 错误。整体在t 时刻的瞬时速度v=at，重力的瞬时功率P重=mgvsin θ，解得P重=mgasin θ·t，因此P重-t 图像是一条过原点的倾斜直线，选项C 错误。在整体沿斜面下滑位移x 的过程中，根据动能定理得Ek=（mgsin θ-μmgcos θ）x，因此Ek-x 图像是一条过原点的倾斜直线，选项D正确。

答案：D

例3 如图4所示，足够长光滑斜面倾角为θ，在沿斜面向上的恒力F 作用下，物体从斜面底端由静止开始向上运动，当物体滑动到某一高度處时撤去恒力F。以地面为零势能面，设物体的重力势能为Ep，机械能为E，则在物体沿斜面向上运动的整个过程中，如图5所示的Ep 和E 随时间t变化的图像正确的是（ ）。

汽车的加速度逐渐减小至0，汽车做加速度逐渐减小的加速运动，因此v-t图像的斜率先保持不变，再逐渐减小。当汽车的加速度减小为0时，汽车做匀速运动，速度达到最大值，且最大值等于v1，以后汽车以速度v1 做匀速运动，因此v-t 图像是一条平行于t 轴的直线。

答案：C

例5 如图7所示，均匀带正电的金属圆环竖直放置，A、B 两点是其轴线上关于圆心对称的两点。某时刻一个电子仅在静电力作用下从A 点沿轴线向右运动至B 点，在此运动过程中，电子的v-t 图像可能是（ ）。

解析：均匀带正电的金属圆环圆心处场强为0，轴线上无穷远处场强也为0，故在圆心与无穷远之间轴线上某点的场强存在最大值。若A 点在场强最大点左侧，根据eE =ma 可知，电子仅在静电力作用下由A 点沿轴线运动至B 点的过程中，电子的加速度先增大，后减小到0，再反向增大，然后反向减小。根据v-t 图像的斜率表示加速度可知，图像斜率先正的增大，后正的减小到0，再负的绝对值增大，然后负的绝对值减小，选项A正确。若A 点在场强最大点右侧，则电子仅在静电力作用下由A 点沿轴线运动至B 点的过程中，电子的加速度先减小到0再反向增大，因此v-t 图像的斜率先正的减小到0，后负的绝对值增大，选项B、C正确，D错误。

答案：ABC

三、通过分析函数图像特殊点的情况选择函数图像

先分析函数图像上的某些特殊点，再根据这些特殊点的情况可选出符合题意的图像。例如，选质点做简谐运动时的图像，如果能够判断出做简谐运动的质点在t=0时刻的振动情况，那么就能选出该质点的振动图像。

例6 如图9甲所示，一列简谐横波以速度v=1 m/s沿绳子由A 点向B 点传播，质点A、B 间的水平距离x=3 m。若t=0时刻，质点A 正从平衡位置向上振动，其振动图像如图9乙所示，规定向上为正方向，则t=0时刻质点B 的振动图像是如图10所示四个选项中的（ ）。

解析：根据图9乙可知，质点A 做简谐运动的周期T=4 s，则波长λ=vT=4 m，A、B 两质点间的水平距离x=3 m=34λ。t=0时刻，质点A 正从平衡位置向上振动，波由A 点向B 点（向右）传播，因此可画出如图11所示t=0 时刻的波形图。t=0 时刻，x =3 m 处的质点B正好位于波峰，与图10中选项D的图像相对应。

答案：D

四、通过定性或半定量分析选择函数图像

定性或半定量分析法是一种粗略地确定研究对象是否具有某种性质，或确定某一物理量变化范围的研究方法。遇到不好找出函数表达式的选函数图像问题，合理应用这种方法能避免陷入对细枝末节的过度分析。

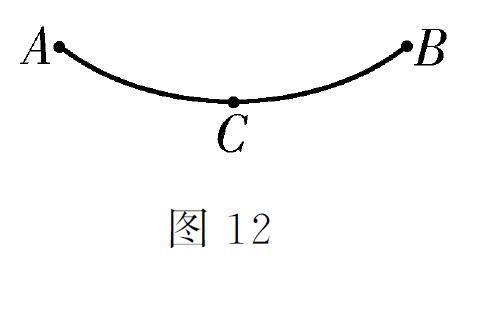
例7 如图12所示，ACB 是一段竖直放置的光滑圆弧轨道，A、B两点等高，相距为0.62 m，距轨道最低点C 的竖直高度为0.01 m。一小滑块（可视为质点）从A 点由静止释放并开始计时，其速率v 随时间t 变化的图像可能是如图13所示四个选项中的（ ）。

解析：设圆弧轨道AC 对应的圆心角为θ，圆弧轨道半径为R，根据几何关系得R2-（R -h）2 =（x/2）2，其中h =0.01 m，x =0.62 m，解得R =4.81 m，则sin θ=0.31/4.81=0.064。因此圆弧轨道AC（或CB）对应的圆心角很小，小滑块在圆弧轨道上的往复运动可视为简谐运动（属于单摆模型），其周期T=2π根号下（R/g）=4.4 s，小滑块从A 点由静止释放后，在0～2.2 s（前半个周期）内，小滑块的速率先增大后减小，在2.2 s～4.4 s（后半个周期）内，小滑块的速率仍然是先增大后减小，与图13中选项A 的图像相对应。

答案：A

总之，求解选函数图像问题，可以根据函数表达式与函数图像相对应选择，也可以根据函数图像斜率表示的物理量，结合图像斜率的变化选择，还可以根据函数图像特殊点的情况或利用定性与半定量分析法选择。

（责任编辑 张 巧）