等效转化思想在“液面照亮区域面积问题”中的应用

杨高轩

高中物理科学思维是从物理学视角对客观事物本质属性、内在规律及相互关系的认识方式;是基于经验事实建构理想模型的抽象概括过程;是分析综合、推理论证等科学思维方法的内化。等效转化是一种建构模型的重要思维方法，要求从两个事物之间的等同效果出发，把复杂的物理问题等效转化为简单的物理问题，从而找到解决问题的途径。

将光源置于液体中，光在液面处会发生折射或全反射，从液面上方观察，有部分液面区域有光线射出而被照亮，如何计算这部分区域的面积呢？ 下面我们就一起来探讨吧！

一、点光源

点光源发出的光是辐射状的，若空间足够大，则是以点光源为球心的球体，对于液面而言，被光照亮的部分是以点光源的正上方对应的点为圆心的圆形。

1.单色点光源。

例1 如图1 所示，半径为R 的圆柱形玻璃容器中装有折射率为根号下2的透明液体，底面圆心O 处有一点光源，容器的高度h 是截面半径R 的一半。从圆柱形玻璃容器上表面观察，液面被光照亮的面积是多少？ （用R 表示）

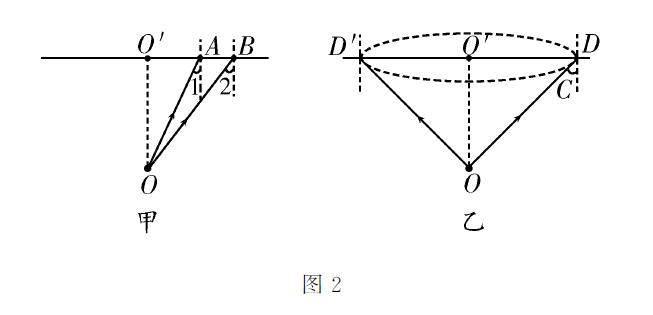
分析：设点光源的正上方对应的点为O'，从点光源射到液面A 点和B 点的两条光线如图2甲所示，根据几何关系得∠2>∠1，即从O'点向外光线的入射角逐渐增大，当入射角等于發生全反射的临界角C 时，点光源发出的光在液面处恰好发生全反射。如图2乙所示，设液面上恰好发生全反射的位置为D 、D'点，则液面被光照亮的部分是以O'为圆心、以O'D（O'D'）为半径的圆形。

解：根据折射定律得sin C =1/n，解得C=45°。根据几何关系得tan C=O'D/h ，解得O'D =h =R/2。因此液面被光照亮的面积S=πR2/4 。

2.复色点光源。

例2 如图3甲所示，S 是水下深度为d 处的一个点光源，它发出两种单色光a 和b，在水面上形成了一个被照亮的圆形区域，其中间区域为复色光形成的，周边的环状区域为单色光形成的，如图3乙所示（俯视图）。已知水对单色光a 和b 的折射率分别为n1和n2（n1

分析：设点光源S 的正上方对应的点为O，根据折射定律sin C=1/n可知，单色光a 发生全反射的临界角Ca 大于单色光b 发生全反射的临界角Cb。如图4 所示，设单色光a在A、A'点恰好发生全发射，单色光b 在B、B'点恰好发生全反射，则单色光a 在水面照亮的区域是以O 为圆心、以OA （OA'）为半径的圆形，单色光b 在水面照亮的区域是以O 为圆心、以OB（OB'）为半径的圆形，环状区域内只有单色光a。