问题解决模式下高中数学复习课教学

王智星

摘要：在高中数学复习课教学中，引入问题解决理念，尝试搭建开放式问题学习和探究情境，从问题启思、合作讨论、追问溯源、回问总结中，可更好地帮助学生全面掌握数学知识点.

关键词：高中数学；问题解决模式；复习课教学

中图分类号：G632文献标识码：A文章编号：1008-0333（2024）12-0035-03

复习课，顾名思义是对所学章节知识点的再现与回顾，也是高中数学重要课型之一.对于复习课的设计，总体上聚焦章节内知识点的逻辑关系，帮助学生认识、理解数学思想和解题方法，升华学生数学学习能力[1].问题解决模式，最显著特点是将“问题”作为课堂教学的主线，引领学生去发现问题、思考问题、探索问题、解决问题.依托问题解决模式教学，可以强化学生对数学问题的学习力、思维力和解题力.

1 问题的提出

问题解决模式是数学学科素养落地的有效途径，能够让学生从问题解决中获得必备品格和关键能力.高中数学学科，数学抽象、逻辑推理、数学建模、数学运算、数据分析、直观想象等都是必备素养，而这些素养的获得，可以通过问题解决教学模式来实现.

本节课程的教学设计以“直线与方程”复习课为例，引入问题解决模式.问题的选择由学生提，解决思路的确定由学生想，解题方法由学生说.课堂由“四问”构成，即启问、探问、追问、回问，依托问题情境，激活数学课堂.考虑到一节课课程容量的有限性，本节复习重点渗透“大单元”理念，从“直线”学习入手，探究与“直线”相关的解题方法，再延伸到对一般“曲线”的解题路径.让学生体认“坐标法”在解决几何问题中的重要价值，感悟数形结合思想的运用.

2 案例呈现与教学过程分析

在对“直线与方程”章节复习课设计上，按照循序渐进的认知规律，将整个课程分为浅度开放、中度开放、深度开放三个环节，每一环节均由问题展开.通过问题来解释本章节知识点，在问题解决中探究数学解题思路和方法，让学生认识、掌握“坐标法”，并抓住高中数学解析几何问题的解题精髓.

2.1 浅度开放设计环节

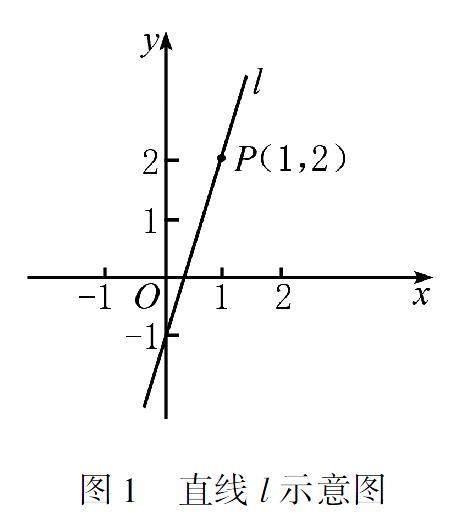
在课堂伊始，引出问题：对本节所学的直线，请回忆并思考，采用的是什么方法？在直角坐标系中，对于直线，需要通过两个坐标点来确定.如图1所示，点P的坐标为（1，2），有直线l经过点P，请思考，再增加一个条件，来确定并求出该直线l所对应的方程.显然，复习课设计，教师所设定的问题，要指向本节主要知识点.对于“直线”的学习，认识直线的构成要素，了解直线方程及表示方法，分析直线与直线之间的关系，等等.

在本例中，有学生想到，可以增加“斜率”条件来确定直线l所对应的方程；有学生想到，可以增加“某一个点”的坐标，来确定直线l所对应的方程；还有学生想到，可以增加“截距”来确定直线l所对应的方程.斜率、点、截距，都是本节所涉及直线方程所要考慮的知识点.在课堂上，为了便于学生对相关问题完成解答，结合学生的回答分别给出相应条件，让学生对照条件，来推导出直线l所对应的方法.

问题1：当增加的斜率为“2”时，则该直线方程如何表达？

问题2：当直线l同时经过点P（1，2）、点Q（3，0）时，直线方程如何表达？

问题3：当直线l在x轴、y轴上的截距相等时，直线方程如何表达？

问题1的解题思路：已知条件有点P坐标，还有斜率k，则根据直线方程表达式y=kx+b，代入方程求出b的值，则推导出该直线l所对应的方程；对于问题2：根据点P、点Q两个点所对应的坐标，可以分别代入直线方程y=kx+b，求出k、b的值，即得到直线方程；对于问题3：给出的条件是经过点P的坐标，还有与x轴、y轴截距相等.在两轴上，截距相等，可以有多种情形，而不同情形所对应的直线方程也不同.比如，当直线l过点P，并在第二象限与x轴、y轴截距相等时，可以计算出直线的斜率为“1”，还可以在第一象限、第四象限共计三种情形.可见，截距相等关系具有开放性，需要学生能够打开思维，考虑多种情况下的直线方程.

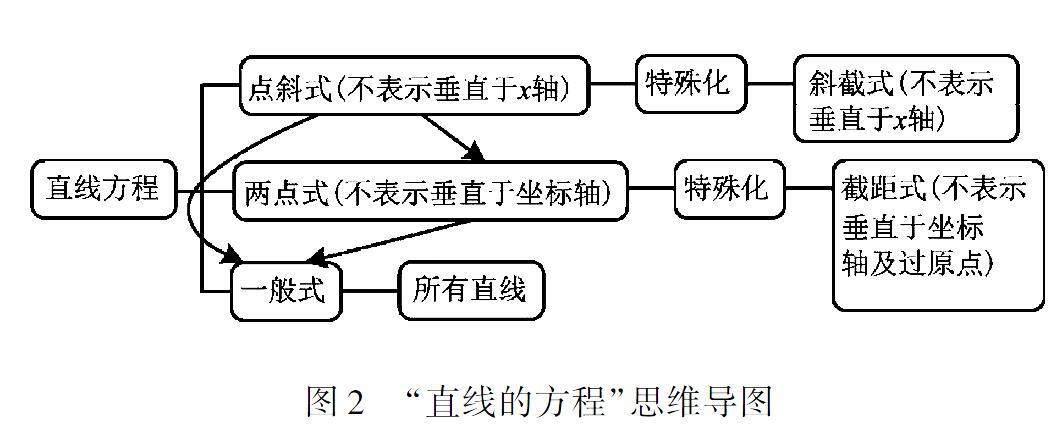
最后，引出“回问”，从上述直线方程的求解中，请学生思考：表示直线方程有哪几种形式？这些形式能否表示平面内的所有直线？直线方程之间能互化吗？在组织学生对直线方程表达形式的讨论后，对所复习的知识点进行综合，借助思维导图来厘清知识点之间的逻辑关系如图2所示.

对直线方程的表达方式主要有三种，即点斜式、两点式、一般式.考虑到特殊情况，对垂直于坐标轴的情形除外.点斜式中，还存在斜截式情形；两点式中，还存在截距式.对于一般式，则可以表示平面内的所有直线.

2.2 中度开放设计环节

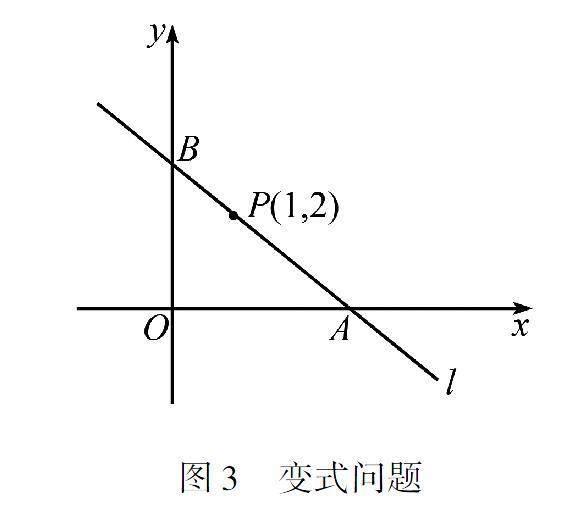
复习课上，对问题解决模式的应用，所设置的问题还要强调对学生问题意识、质疑精神的激发，让学生能够从问题解决中积累数学知识经验.关于“直线与方程”章节的复习，引入变式问题，如图3所示.

某直线l过点P（1，2），与x轴、y轴相交于A、B两点.请思考，增加某一条件，来确定直线并求出直线l所对应的方程.问题的引出，要给予学生思考的时间.教师要适当启发学生，联系本章所学的知识点，翻阅教材，拓宽思路.对该问题的设计，意图在于让学生选择恰当的方式来求解直线方程.题意中，直线的位置具有开放性，为学生讨论、探究搭建了空间.对相关题型的回忆，有学生想到了“待定系数法”.将学习主动权交给学生，鼓励学生展开交流、碰撞思维，突出“学中做”“做中学”.对方程思想的学习，有助于学生主动去发现、分析和解决问题.有学生根据题设已知条件，想到了三角形的周长、面积、线段PA=2PB、向量PA·PB等条件，让一道题目变成了多道题目.

比如，结合图3，当S△AOB=3时，求直线l所对应的方程.在解析中发现，当△AOB的面积为3，所得结果无解.有学生对“无解”感到疑惑，怀疑自己是不是解错了.通过检验，之所以出现“无解”情形，主要是因为三角形的面积，与边长有一定范围有关.如果改变面积值，再对比有解的条件下，求出直线l所对应的方程.在这个过程中，对于三角形的面积，又适度延伸新的数学问题“最值问题”.

再如，某例题中，过点P（1，2）的直线l与x轴、y轴交于A、B两点，当△AOB面积最小时，直线l所对应的方程是什么？针对条件△AOB面积最小，学生需要运用不等式来求解，最终得出直线方程为2x+y-4=0.对该题进行变式训练，同样过点P（1，2）的直线l，再给出l′所对应的方程为x+y-5=0.请思考，对这两条直线，可以提出哪些问题？这一设计旨在转变教学重点.前面所讲内容，侧重于对直线方程的求解方法，接下来，通过两条直线方程，让学生思考直线与直线之间的位置关系.在平面坐标系中有两条直线，以提问的方式，带领学生复习两条直线的位置关系问题，进而渗透数形结合思想、方程思想，夯实学生的“四能”.

学生通过回顾，同一平面内，两条直线的位置关系有三种，即平行、垂直、相交.对已知直线l与直线l′，前者的条件有过点P的坐标，后者有具体的直线方程.由此，学生对这两条直线编写问题如下：当直线l与l′平行时，直线l所对应的方程是什么？在解法上，两条直线平行，则具有相同的“斜率”，可以根据l′的斜率，点P（1，2）的坐标，得到直线l方程.还可以编写问题如下：当直线l与l′垂直时，直线l所对应的方程是什么？在解法上，两条直线垂直，根据两个斜率乘积之值为“-1”，可以据直线l′的斜率，得出直线l的斜率，进而求解出直线l的方程.还可以编写问题如下：当直线l与l′相交时，求解直线l的斜率k的取值范围.这一问题的设计具有开放性，两直线相交，交点的位置有几种情况？如果两条直线的交点在第一象限，则直线l的斜率k取值范围是多少？

2.3 深度开放设计环节

前面两个环节所设计的问题，利用变式训练为学生创设多种可能的解题空间.接下来，走向深度的开放题设计：某题中，已知点P（1，2），直线l′对应的方程为x+ty-5=0.据此，可以提出哪些问题？该题题设条件y项系数由“1”变成了“t”，将固定的直线变成了可动的直线.再对照点P的左边，一个点与一条可变的直线之间，有学生想到了利用点到直线的距离来设置问题，也有学生想到了定点问题.这些问题，其设计较为简单.比如，某直线l′，恒过某定点；或者，某直线l′，求点P到该直线的距离最大值.

教师通过启发，让学生从“代数”视角，再延伸新的问题.比如，在坐标系中，有直线l′，对应方程为x+ty-5=0，直线l，对应方程为tx-y-t+2=0.当这两条直线相交于点Q，可以提出哪些问题？直线l′和直线l都变成了动线，由前面的“一动”过渡到“两动”，让学生运用直线的性质，来分析两条可动直线之间的关系.显然，对该题提出问题，难度较大，对两条动态直线的讨论，进一步提升学生的“四能”能力.如图4中，直线l′与直线l相较于点Q，求△QAP的面积最大值.

据直线l′方程可知，该直线交x轴于点A（5，0）该点为恒定点.据直线l方程可知，该直线恒过定点P（1，2）.再对照图形可知，两直线始终处于垂直状态.由此可得，两直线垂直，则可以根据线段QA與QP的长度，得到△QAP的面积.再对该题进行变式训练，当直线l′与直线l相交于点Q，求点Q的轨迹图形是什么？

3 结束语

问题解决模式下的复习课教学，教师要对接“四基”和“四能”.借助章节主要知识点，通过问题变式设计，指导学生分析、思考、解决数学问题.

参考文献：

［1］ 孙丙虎，葛勇.高中数学中“智慧课堂，问题解决”复习课教学模式探究[J].读写算，2020，1181（34）：111-112.

［责任编辑：李璟］