双周期参数系统的受迫振动响应*
2024-05-24顾京君童彤黄迪山
顾京君 童彤 黄迪山
(1.南通振康机械有限公司,南通 226153)
(2.上海大学 机电工程与自动化学院,上海 200444)
引言
谐波减速器广泛应用于各种机器人关节,它由柔轮、刚轮、波发生器三大基本构件组成.波发生器镶套在柔轮内圈,柔轮齿与刚轮齿进行内啮合,柔轮齿数比刚轮齿数少,因此,它是一个少齿差传动机构.其中,波发生器由椭圆凸轮外套柔性滚动轴承组成,基本结构如图1所示.

图1 单刚轮谐波减速器基本结构Fig.1 Basic structure of single rigid wheel harmonic reducer
在制造过程中,如果柔轮齿与刚轮齿引入了周节累积误差,则谐波减速器在动力传递中将出现双周期时变扭刚度波动,形成双周期参数振动问题.
关于单自由度参数系统振动,学者王建军等[1,2]利用Sylvester理论和Fourier 级数给出了自由和受迫振动响应的级数解;Sinha[3]基于雪比多夫多项式,推出逼近级数解;Ivana Kovacic[4]回顾了几种典型参数激励下的稳定性区域求解.近几年,利用组合频率三角级数法[5,6]应用于多自由度参数振动分析,确定了自由与受迫振动响应的解析逼近.而大多数文献研究内容在基于Floquet理论上讨论参数振动稳定性问题[7-11].但是,对于双周期参数振动的响应预测问题,仍然需深入探讨.
本文针对电机、谐波减速器和惯量负载传动问题,建立双周期参数振动方程,引入基于组合频率的二重三角级数,对其响应进行级数逼近解研究.
1 动力学建模与二重三角级数逼近
在电机、谐波减速器和惯量负载传动中,考虑双周期时变扭刚度波动,建立双周期参数振动方程;对于受迫振动求解,由等效动力学模型,提出基于组合频率的二重三角级数逼近.
1.1 双周期参数振动方程
如图2所示的是一个谐波减速器的刚度曲线K0(t),它可以认为在基础刚度Km上叠加了两个频率不同的刚度波动,其数学表达为

图2 双周期时变扭刚度曲线K0(t)Fig.2 Dual period time-varying torsional stiffness curve K0(t)
K0(t)=Km(1+β1cosω1t+β2cosω2t)
(1)
式中,ω1和ω2均为刚度波动频率,又称参数频率;β1和β2为调制指数.
由于两个扭刚度波动的周期不同,但它们相互接近,导致扭刚度波动曲线呈拍频状(图2).
在谐波减速器传动中,电机、谐波减速器和惯量负载构成双惯量弹性负载系统,如图3所示.

图3 双惯量弹性负载系统Fig.3 Elastic loading system with dual inertia
双惯量弹性负载系统的扭振动方程为
(2a)
(2b)
在方程(2)中,形成的刚度矩阵将为半正定,因此,双惯量弹性负载系统存在一个零固有频率.
对等式(2a)乘以J2/J1减去(2b)的代数运算,得到不含刚体位移的振动方程.
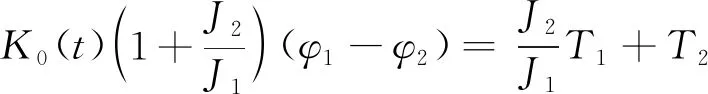
(3)

=T(t)
(4)
式中,θ为两个惯量之间的扭转角,力矩T(t) =T0+Tcosωpt来自于电机驱动.其中,T0是电机恒力矩;Tcosωpt是电机力矩波动,ωp为力矩波动频率,一般它与电机轴转频相同.
1.2 双周期参数振动响应解形式
改写参数振动方程(4)为以下形式
=T(t)-K(β1cosω1t+β2cosω2t)θ
(5)
根据等式(5)表达,双周期参数系统的等效动力学模型是一个双调制反馈控制系统,如图4所示.

图4 双周期参数系统的等效动力学模型Fig.4 Equivalent dynamic model of double periodic parameter system
在双调制反馈控制系统中,振动响应θ(t) 同时被频率ω1和ω2所调制,其频率被裂解,在叠加以后,反馈至系统的输入端.通过连续交错地频率裂解和组合过程,在振动响应θ(t)中,存在一系列组合频率ω+mω1+nω2谐波分量(m=-∞,…,-1,0,1,…,∞,n=-∞,…,-1,0,1,……,∞).因此,双周期参数系统振动响应θ(t) 可以用基于组合频率ω+mω1+nω2的二重三角级数加以逼近,即响应的数学表达式(6).
Fm,ne-j(ω+mω1+nω2)t]
(6)
当外激励力T(t)=0时,对应着双周期参数系统的自由响应,式(6)中的ω为主振荡频率,即ω=ωs;当力矩T(t)≠0,θ(t)对应着双周期参数系统的受迫振动.如果外激励力T(t) =Tcosωpt时,则ω=ωp.
在图4的系统输出中,由于振动响应能量的有限性,能量主要分布在频率ω附近,随着三角级数项m→∞或n→∞,则谐波系数Em,n→0和Fm,n→0.因此,对于振动响应逼近,可以采用有限项二重三角级数计算替代无限项级数的逼近.
2 受迫振动响应求解与计算
在双周期参数系统受迫振动的二重三角级数逼近中,采用矩阵降维法,实现对受迫振动的谐波系数Em,n的求解,得到受迫振动响应解.
2.1 谐波力矩作用下受迫振动
若双周期参数系统受迫振动方程(4)为
=Tcosωpt
(7)
对于系统的受迫振动,其响应解形式为
Fm,ne-j(ωp+mω1+nω2)t]
(8)
将响应解形式(8)和欧拉公式代入方程(7),对方程两边作谐波平衡,从正复指数ej(mω1+nω2)t部分,得到关于不含时间变量的谐波系数Em,n的递推式.
当m=0 和n=0时
(9)
一般情况下,谐波系数Em,n的递推式为
J(ωp+mω1+nω2)2+jC(ωp+mω1+
(10)
其中m=-k,…,-1,0,1,…,k和n=-k,…,-1,0,1,…,k.
这样,(2k+1)×(2k+1) 个Em,n的递推式构成了代数方程(11).
ZE=P
(11)
式中,Z为2k+1阶三维系数矩阵,E为待求的2k+1阶二维谐波系数矩阵,P为 2k+1阶二维力矩阵.在公式(11)中,考虑了三维系数矩阵Z的阶数m足够大时,即m→∞,谐波系数Em+1,n→0,Em,n+1→0,E(m+1),-n→0和E-m,-(n+1)→0.
为了矩阵Z、E和P降维,对于式(10)中的常数项,记
ϖm,n=K-J(ωp+mω1+nω2)2+
jC(ωp+mω1+nω2)
(12)
引入子矩阵
(13)
(14)
谐波系数子向量Eh
Ek=[E-kh…E-1hE0hE1h…Ekh]T
(15)
力矩子向量P0
P0=[0 … 0T0 … 0]T
(16)
将式(12)代入谐波系数Em,n递推式(9)和(10);取h=-k,…,-1,0,1,…,k,将子矩阵和子向量式(13)至(14)按下标从-k至k依次在平面上排列,由此,把三维代数方程(11)展成为二维代数方程(17).
(17)
记为
(18)

同理,从负复指数e-j(mω1+nω2)t部分,可以得到另一组谐波系数Fm,n.其中,谐波系数Em,n与Fm,n互为共轭.
2.2 振动响应计算
在双惯量弹性系统中,外界激励力矩分两部分,一是恒定力矩T0,这时ωp=0;另一个是力矩波动,力矩波动频率ωp=ω1(一般电机力矩波动为恒定力矩的5%).在不考虑负载力矩情况下,对于双惯量弹性负载系统的受迫振动响应,将按谐波力矩和恒力矩两种情况进行讨论.
在双惯量弹性负载系统(7)中,设惯量J=1,阻尼系数C=2.64,平均刚度K=17410,总扭刚度K(t) 曲线如图2所示; 参数频率一ω1=2πf1,f1=10.125Hz,调制指数一β1=0.06;参数频率二ω2=2πf2,f2=10Hz,调制指数二β2=0.07 .
算例1: 若驱动谐波力矩(电机驱动力矩波动)波幅T=0.5,激励频率ωp=ω1,计算双惯量弹性负载系统的受迫扭振动响应.
取级数项m=-11,…,-1,0,1,…,11,n=-11,…,-1,0,1,…,11.根据所给的动力学参数,由公式(18)计算谐波系数矩阵中元素Em,n,在频率ωp附近的部分谐波系数数据列于表1.

表1 算例1中部分谐波系数Em,n计算值
于是,该双惯量弹性负载系统受迫扭振动响应θ1(t) 表达为:
设置时间起点为0,步长0.001秒,时间历程为100秒,根据上述双惯量弹性负载系统受迫扭振动的响应表达,计算该系统受迫振动响应时间历程θ1(t)和频谱Θ1(ω),结果如图5所示,其中,振动响应有效值0.0318m·rad.

(a) 扭振动响应时间历程θ1(t)
系统在外界激励力矩作用下,从振动响应频谱Θ1(ω)可以看到,在各主谐峰(基频ωp的高阶谐频)的左右侧和直流分量的右侧,存在着密集型的边频族分布.
算例2: 在恒力矩驱动下,计算双惯量弹性负载系统的受迫扭振动响应.
设恒力矩力幅T0=10,这时驱动频率ωp=0,根据所给动力学参数,从式(18)计算谐波系数矩阵中元素Em,n,部分计算值见表2.

表2 算例2中部分谐波系数Em,n计算值
于是,受迫扭振动响应θ2(t)表达为
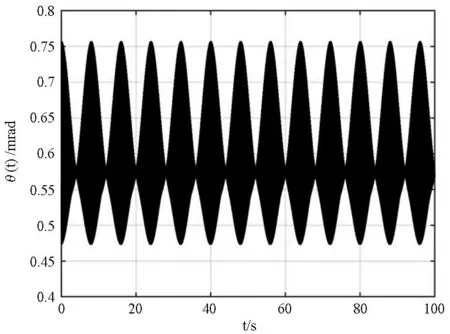
设置时间起点为0,步长0.001秒,时间历程为100秒,根据上述响应表达,计算该双惯量弹性负载系统受迫扭振动响应,其中振动响应时间历程θ2(t)、响应频谱Θ2(ω)结果如图6所示,振动谱特征与例1中的类同.其中,振动响应有效值0.0613m·rad.
(a) 扭振动响应时间历程θ2(t)
与线性系统不同,双周期参数系统在恒力矩驱动下,仍然产生稳态的扭振动响应,而且,恒力矩越大,扭振动响应越大.
3 双周期参数振动特征
无论在算例1还是在算例2,在受迫振动响应谱中,都存在着密集型的边频分布,形成双周期参数振动响应特有的边频族特征.以算例2为例,对受迫振动响应谱图作局部放大处理,如图7所示.
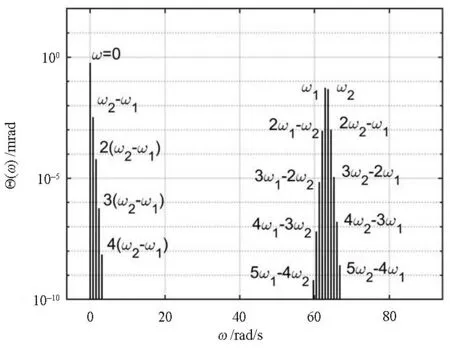
图7 恒力矩驱动下的扭振动频谱局部放大图Fig.7 Local enlarged figure of torsional vibration spectrum under a constant torque
在直流分量附近,存在5个数量级较大的边频分量,它们分别是0、ω1-ω2、2(ω1-ω2)、3(ω1-ω2) 和4(ω1-ω2);在第一个谱族附近,存在10个数量级较大的边频分量,它们分别是5ω1-4ω2、4ω1-3ω2、3ω1-2ω2、2ω1-ω2、ω1、ω2、2ω2-ω1、3ω2-2ω1、4ω2-3ω1、5ω2-4ω1;在第二、三、四个谱族附近,同样存在这种密集型边频族现象.双周期参数系统的受迫振动响应频谱具有丰富的边频,形成组合频率特征的边频族,谐波分量具体数值详见表2,其中边频间隔 Δ=ω1-ω2为两个参数频率之差.
为了验证组合频率特征边频族的客观存在性,搭建谐波减速器试验台,对一批双刚轮谐波减速器试验样件,在试验台架上进行扭振实测.其中的一个试验样件,柔轮齿与刚轮齿都有较大的周节累积加工误差,扭振测试结果如图8所示.在扭振动频谱局部放大图中,组合特征边频谱现象明显.其中,f1=34Hz,f2=33.58Hz,边频间隔约为Δ≈0.42Hz.
实验表明:对于周节累积加工误差谐波减速器扭振,采用双参数振动建模,振动理论谱与实测结果一致性好,反映了动力学建模的有效性.
4 逼近计算误差
为了评估三角级数逼近计算精度,根据公式(7),定义逼近误差为:
(19)

力幅T大小影响逼近误差,所以采用逼近计算误差ε(t)考核计算精度
(20)
算例1的逼近计算误差时间历程ε(t),如图9所示,逼近计算误差ε小于5e-13 (参考Runge-Kutta法计算误差小于1e-3).因此,用二重三角级数逼近双参数系统振动响应,其逼近计算精度足高.
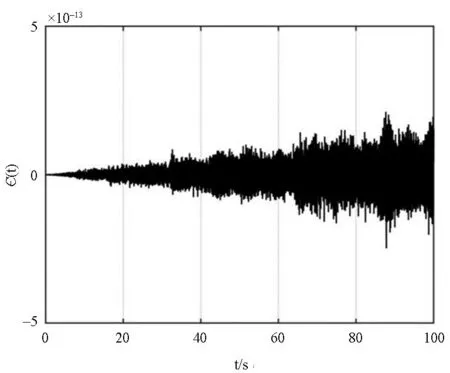
图9 算例1中逼近计算误差时间历程ε(t)(k=11)Fig.9 Time history of approximation error in example1 ε(t)(k=11)
当然,双周期参数振动响应的逼近计算误差与二重三角级数逼近的项数有关,当级数逼近项数越多,逼近计算误差越小, 同时,计算机耗时也越多.
5 小结
在谐波传动中,如果柔轮齿与刚轮齿同时引入了周节累积误差,则谐波减速器在动力传递中将出现双周期参数振动问题.
基于组合频率的二重三角级数,可以对双周期参数系统受迫振动响应进行逼近,得到不含时间变量的谐波系数递推式,形成三维矩阵代数方程.通过引入中间变量,矩阵重新排列,对三维矩阵方程进行降维计算,实现对双周期参数系统的受迫振动响应谐波系数的求解,算法行之有效,并且准确性好.
通过计算分析可知,双周期参数系统受迫振动响应具有密集型组合频率边频族的特征,其中边频间隔Δ=ω1-ω2,为两个参数频率之差.
