带裂纹石墨烯增强金属泡沫梁的振动特性研究*

2024-05-24石兴东程鹏张宇飞

动力学与控制学报 2024年3期

石兴东程鹏张宇飞,2†

(1.沈阳航空航天大学航空宇航学院,沈阳 110136)

(2.广西大学土木建筑工程学院,南宁 530004)

引言

金属泡沫材料由于内部孔隙的存在,具有轻质、隔热、减震的特性,通过定制内部孔隙的密度和尺度,可以获得所需的材料力学性能,因此,金属泡沫材料在能量吸收、轻质结构和热控制[1]等方面得到了广泛的应用.然而,多孔材料的内部孔隙降低了结构的强度和刚度,这限制了其在某些工程领域的应用.相关研究[2]表明,多孔材料可以填充低体积分数的碳材料,如石墨烯薄片(GPL)和碳纳米管,以弥补其强度和刚度的降低,特别是GPL增强复合材料[3,4]具有轻质、良好的导电和导热性能,因此,关于GPL增强复合材料结构的研究受到了广泛的关注.

Kitipornchai等[5]研究了GPL增强多孔梁的自由振动特性.Ye和Wang[6]研究了FG-GPLRMF薄壁圆柱壳的非线性强迫振动特性.Yang等[7]基于切比雪夫-里兹方法分析了GPL增强多孔纳米复合板的屈曲和自由振动.Dong等[8,9]研究了GPL增强多孔纳米复合圆柱壳的屈曲和线性振动行为.Wang等[10]分析了GPLRMF圆柱壳的非线性自由振动特性.Yang和Chen[11]分析了裂纹对不同边界条件下功能梯度材料Euler-Bernoulli梁振动和屈曲的影响.刘涛等[12]分析了轴向运动功能梯度梁的横向振动频率特性.周磊[13]以含裂纹石墨烯增强功能梯度层合梁为研究对象,进行了动力稳定性行为分析.刘金建等[14]基于欧拉梁理论,研究了轴向运动功能梯度粘弹性梁横向振动的稳定性问题.

虽然一些学者已经对石墨烯增强多孔结构开展了研究,但关于带裂纹石墨烯增强金属泡沫梁振动问题的研究尚未开展.本论文基于Timoshenko梁理论,研究带裂纹功能梯度石墨烯增强金属泡沫梁(FG-GPLRMF)的自由振动问题,包括控制方程推导和微分变换法的应用,研究了裂纹深度、裂纹位置、GPL几何尺寸、孔隙类型、GPL分布和长细比对带裂纹FG-GPLRMF梁自由振动特性的影响.

1 材料特性与旋转弹簧模型

1.1 材料特性

图1(a)是长度为L、厚度为h的两端固定的Timoshenko梁模型,在距左端L1处包含一个深度为a的边缘裂纹.

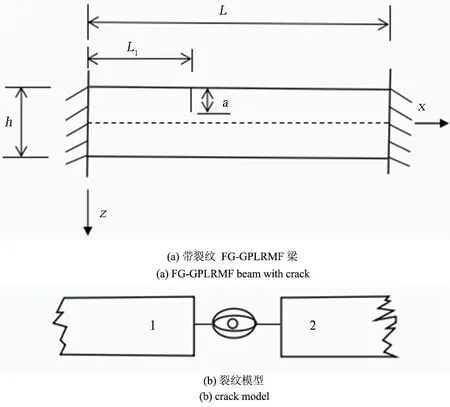
图1 裂纹梁结构Fig.1 Configuration of cracked beam

沿梁高度方向考虑了三种孔隙分布类型[10],即孔隙-a、孔隙-b和孔隙-c.孔隙-a和孔隙-b在梁高方向上呈对称分布.孔隙-a和孔隙-b的差异在于前者的中平面孔隙最大,后者的中平面孔隙最小.孔隙-c的孔隙大小均匀分布.

考虑了三种不同GPL分布方式[10],对于GPL-Ⅰ和GPL-Ⅱ,GPL相对梁中平面对称分布.对于GPL-I,最大的体积分数发生在梁的上表面和下表面;对于GPL-Ⅱ,最大体积分数发生在中面.对于GPL-Ⅲ,GPL均匀分布.

FG-GPLRMF梁的杨氏模量EGM(z)和质量密度ρGM(z)分别为[7,15]

(1)

(2)

其中Eg和ρg表示无孔GPL增强金属的杨氏模量和质量密度;P1、P2和P3表示孔隙系数;Pm1、Pm2和Pm3表示质量密度系数.

1.2 旋转弹簧模型

假定裂纹垂直于梁表面,且始终保持开放状态.Timoshenko梁的边缘裂纹造成了弯曲斜率的不连续以及开裂截面的横向位移.已有研究[16,17]表明,与弯曲斜率中的不连续性(I型断裂)相比,横向位移中的不连续性(Ⅱ型断裂)对系统总应变能的贡献要小得多,因此本分析中忽略Ⅱ型断裂的影响.将裂纹截面建模为如图1b所示的无质量弹性弹簧,可将开裂梁视为在开裂截面上由转动弹簧连接的两个子梁,其弯曲刚度为:

KT=1/G

(3)

其中G是裂纹引起的柔度,并且[18]

(4)

其中M为裂纹截面弯矩,K1为I型弯曲荷载作用下的应力强度因子,E(a)为裂纹尖端的杨氏模量,ν为泊松比.

通过拉格朗日插值技术,可以从Erdogan和Wu[19]给出的数据中得到应力强度因子的大小,即

(5)

其中ζ≤0.7意味着仅考虑0至0.7的裂纹深度比.根据式(3)～式(5),可以确定裂纹部分的弯曲刚度.

2 运动方程与微分变换法

2.1 运动方程

(6)

其中U(x,t)和V(x,t)是中平面(z=0)上的位移分量,Θ是梁截面的转动角位移,t是时间.von Kármán型非线性应变-位移关系由下式给出[20]:

(7)

正应力和剪切应力分别为

(8)

这里

(9)

裂纹FG-GPLRMF梁的动能T和势能W为[20]

(10)

(11)

其中ΔΘ为Θ2(L1)-Θ1(L1);Ui、Θi、Vi中的下标i等于1,2,表示被裂纹分割的左子梁和右子梁.最后一项表示旋转弹簧产生的势能.

将式(10)、式(11)中含Q11、Q55和ρGM(z)项定义为:

(12)

其中κ=5/6是剪切修正系数.

哈密顿原理由下式给出

(13)

其中t1和t2分别表示初始时间和最终时间.

引入如下无量纲变量

(14)

其中A110和I10是无孔梁的A11和I1的值.

梁连续性条件

(15)

梁的位移函数设为[21]:

(16)

这里λ是径向固有频率,γ是弦向固有频率.

将式(10)～式(12),式(14)～式(16)代入式(13),即可得到简化后的运动方程:

(17)

2.2 微分变换法

本文将变换函数用大写字母表示,将原函数用小写字母表示.在定义域D中定义一个解析函数g(x),设x=x0表示D中的任意点.函数g(x)的微分变换定义为[15]

(18)

其中,m是截断数.

将Xu[15]中的表1和表2公式代入方程(17)以及两端固定边界条件,可以得到变换函数和对应边界条件.

表1 FG-GPLRMF梁参数[20]

表2 FG-GPLRMF梁弯曲振动固有频率(rad/s)的收敛性

相容方程:

(19)

(20)

(21)

设U1(0) =C1,V1(0) =C2,Θ1(0) =C3,代入变换函数方程和对应边界条件,可以计算Ui(k),Vi(k)和Θi(k)的值.

将Ui(k),Vi(k)和Θi(k)代入对应边界条件方程,可以解出λ.

3 结果和讨论

下面对图1中所示的FG-GPLRMF梁进行研究,参数如表1所示.

FG-GPLRMF梁弯曲振动的固有频率收敛结果见表2,其中以P1=0.5、WGPL=1.0%、GPL-I和孔隙-a为例.结果表明,在m=16时,固有频率趋于收敛,但考虑到精确性,在下面的计算中采用了m= 60.

在图2中,研究了孔隙系数P1对固有频率的作用,其中考虑了不同的GPL分布方式和孔隙分布.随着P1的增加,孔隙-b和孔隙-c梁的固有频率减小.然而,对于孔隙-a梁,其固有频率先减小后增加.造成这种现象的原因是,当梁的几何尺寸保持不变时,固有频率与弯曲刚度(EIy)呈正相关,与单位长度的质量(ρT)呈负相关.进一步计算表明,当P1大于0.4时,弯曲刚度的相对变化小于质量的相对变化.此外,这三种孔隙分布的固有频率中,GPL-Ⅰ分布的固有频率最高,而GPL-Ⅱ分布的固有频率最低.因此,GPL-Ⅰ分布是提高结构刚度最有效的分布方式.以上结果表明,孔隙系数和GPL分布对FG-GPLRMF的自由振动有显著影响.

(a) 孔隙-a

图3给出了GPL重量分数WGPL对不同GPL分布方式和孔隙分布的FG-GPLRMF固有频率的影响.对于不同的GPL分布方式,固有频率随WGPL的增加而增加,其原因就在于增加石墨烯含量可增强梁刚度.通过将极少量的GPL分散到基质中,即可提高多孔梁的有效刚度.与其他分布模式相比,孔隙-a和GPL-Ⅰ分布方式的梁具有最大的固有频率.

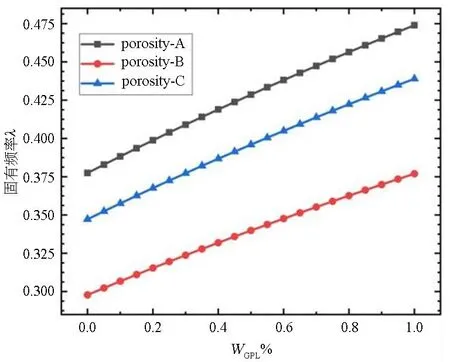
(a) 石墨烯-Ⅰ

图4给出了不同GPL尺寸对FG-GPLRMF梁固有频率的影响.图4(a)为FG-GPLRMF梁的固有频率随GPL长厚比lGPL/tGPL的变化情况.随着lGPL/tGPL的增加,固有频率增加.结果表明,当lGPL和wGPL保持固定时,单个GPL越薄,其刚度强化效果越好.图4(b)为固有频率随GPL长宽比lGPL/wGPL的变化规律.随着lGPL/wGPL的增加,固有频率减小.这表明,石墨烯的表面积越大,刚度增强效果越好.同时,由图4可以看出,当lGPL/tGPL≥102或lGPL/wGPL≥10时,强化效应随这些比值的变化不大.

(a) 长厚比(lGPL=2.5×10-6m,wGPL=1.5×10-6m)

图5研究了裂纹位置对FG-GPLRMF梁的固有频率的影响.结果表明,固有频率对位于梁中心的裂纹最为敏感.当裂纹靠近梁端时,裂纹的影响较小,裂纹位置由梁中心向梁端变化时,固有频率逐渐增加.

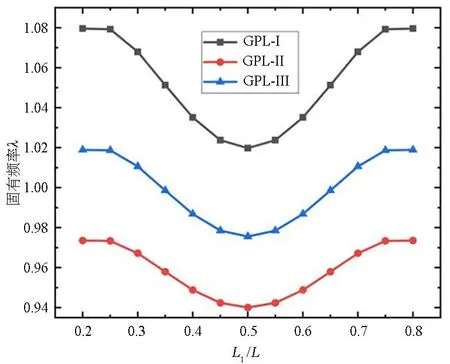
图5 裂纹位置对FG-GPLRMF梁固有频率的影响(孔隙-a;WGPL=0.01;L/h=6;h=0.1;P1=0.5;L1/L=0.5)Fig.5 Effect of crack location on natural frequency of FG-GPLRMF beam (Porosity-a;WGPL=0.01;L/h=6;h=0.1;P1=0.5;L1/L=0.5)

图6研究了裂纹深度对FG-GPLRMF梁固有频率的影响.结果表明,随着裂纹深度增加,梁的固有频率降低,对于不同GPL分布方式,固有频率降低的速度大致相同,不同孔隙下裂纹梁固有频率都逐渐变小,这说明裂纹位置对频率的影响远超其他因素.