基于Vicsek分形结构的智能航天器集群在轨组装动力学与控制*
2024-05-24潘星熠陈提
潘星熠 陈提
(南京航空航天大学 航空航天结构力学及控制全国重点实验室,南京 210016)
引言
太阳帆、大型空间望远镜和大口径天线等大型空间结构将在深空探测、高精度观测和高容量通信等未来空间项目中发挥重要作用.由于火箭运载能力和整流罩的包络原因,此类超大型空间结构一般不能采用折叠收拢发射入轨、在轨展开的方式搭建,在轨组装可以有效解决这个问题.在轨组装是把一个大型空间结构拆分为一组或几组容易构建的模块,互相独立从地面发射后再在太空中进行组装从而搭建成完整结构的技术[1].
微小卫星编队飞行和模块化航天器的研究让标准卫星的功能被一组更小的模块所替代,模块化航天器在太空中的复杂编队激发了学者们利用分形几何结构的兴趣[2],并且研究发现Vicsek分形几何结构也可以用于部署天线阵列[3-5].分形结构具有无限迭代、自相似的、具有分形维数点等特点,这种本身的特性使分形天线具有易于小型化和具有多频特性的特点[6],Vicsek分形天线阵列的自相似性有利于实现多波段特性,同时可增加方向性和控制天线主波束的可能,这给空间通信提供许多好处.此外,分布式望远镜也被认为是解决超大口径望远镜技术限制的有效方法,分布式空间光学干涉技术可以实现等效数十至数百米光学合成孔径[7].美国宇航局和欧洲航天器分别提出了类地行星发现者干涉仪(TPF-I)和达尔文计划,中国也提出了“觅音计划”,均是通过小型望远镜阵列来实现高分辨率成像[8-10].
近些年,学者们提出了多种自主组装概念和方法.美国国家航空航天局兰利研究中心的Rhodes等使用102根四面体桁架和12个六边形面板演示了一种大孔径天线的自动装配过程[11].加州理工学院的Lee等设计了一种基于在轨展开、空间机器人和编队飞行技术的100m模块化空间望远镜架构[12].在美国国防高级研究计划局资助下,劳拉空间系统公司试图使用空间机械臂系统在轨组装一个大型天线反射器[13].虽然我国在轨组装技术研究起步较晚,但是近十几年也提出了一系列任务概念和在轨组装规划.例如,哈尔滨工业大学崔乃刚、郭继峰团队[14]采用了两级递阶智能规划算法设计大型空间桁架结构的在轨装配任务序列.钱学森空间技术实验室和哈尔滨工业大学联合提出了利用空间机器人实现一种模块化巨型空间太阳能电站(SSPS)搭建概念[15].
具有自主机动能力的组装模块在近距离操作过程中,必须要考虑避免碰撞.目前看来,针对无人机和机器人系统的避撞成果较为丰富,但是在针对航天器在轨组装的避撞规划研究相对较少.使用超二次曲面描述组装模块与障碍物,然后利用人工势函数方法设计相应控制器是航天器避撞的常用方法[16,17].Morgan等使用分布式模型预测控制解决了带有时变避撞约束的航天器集群最优导航和构建问题[18].刘建彪等根据MROT理论,规划组员航天器的安全转移路径以规避碰撞危险[19].
本文以在轨组装超大型空间结构为目标,受Vicsek分形图形启发设计了适用于搭建星载天线以及分布式空间望远镜的超大型空间结构,以125个刚性航天器为例研究了智能航天器集群在轨组装动力学与控制问题.考虑中心引力场,分别建立了追踪航天器和目标航天器的位置和姿态动力学方程组.以Vicsek分形为基础结构,设计了125个航天器在轨组装的构型,并且将组装过程分为三阶段完成,其中每个阶段均由预组装环节和完全组装环节构成,在预组装环节引入了避撞力,设计了避撞复合控制器,在完全组装环节采用了纯PD控制,最后通过数值仿真验证了控制策略的有效性.
1 刚性航天器动力学模型与控制
1.1 相关坐标系以及向量描述
如图1所示,Fi≜{Oxiyizi}为地心惯性坐标系,Fc≜{Cxyz}和Ft≜{Txtytzt}分别是与追踪航天器和目标航天器固连的本体坐标系.{r,re}和{rt}分别是表示在Fc和Ft坐标系中的相对位置向量.本文中,控制器是作用在追踪航天器上,因此追踪航天器逐渐靠近追踪目标航天器,并与其对接.

图1 坐标系以及相关向量描述Fig.1 Description of the coordinate frames and defined vectors
1.2 航天器相对惯性系的位置和姿态运动方程
追踪航天器质心C的位置和本体坐标系Fc相对于惯性坐标系Fi的姿态可以通过以下运动学方程来描述[20]:
(1)
(2)
其中r为从地球中心指向追踪航天器的位置矢量,σ为描述追踪航天器姿态的修正罗德里格斯参数(Modified Rodrigues Parameters, MRP);v和ω分别为追踪航天器线速度和角速度.这些量均在追踪航天器本体坐标系Fc中表示.
追踪航天器动力学方程可以描述为:
(3)
(4)
其中fc和τc分别为作用在追踪航天器上控制力和控制力矩,m和J分别为追踪航天器的质量和转动惯量矩阵,μ定义为μ=μg/‖r‖3,其中μg为地球的引力常数.对于任意向量x=[x1,x2,x3]T,S(x)定义为

(5)
同样,无外力和外力矩作用下自由翻滚的目标航天器的位置和姿态运动方程为:
(6)
(7)
(8)
(9)
其中rt,σt,vt和ωt分别为目标航天器的位置矢量、基于MRP的姿态描述、线速度和角速度;mt和Jt分别为目标航天器的质量和转动惯量矩阵.这些量均在目标航天器本体坐标系Ft中表示.其中μt定义为μt=μg/‖rt‖3.
1.3 航天器相对惯性系的位置和姿态运动方程
由于两航天器的位置和姿态等向量分别定义在两个不同的坐标系下,在计算相对参数时需要把向量转换到同一坐标系下.从目标航天器本体坐标系Ft到追踪航天器本体坐标系Fc的旋转矩阵为:
(10)
其中用MRP表示的追踪航天器与目标航天器的相对姿态σe定义为:
(11)
根据图1所示,在追踪航天器本体坐标系中,两航天器之间的相对角速度,相对距离和相对速度可以分别表示为:
ωe=ω-Rωt,re=r-Rrt,ve=v-Rvt
(12)
2 控制器设计与任务规划
2.1 Vicsek分形结构
分形几何图形是通过在简单的起始拓扑上执行的迭代过程生成的.分形图形具有无限迭代、自相似等特点,在航天器在轨组装领域充分发挥其优点,有利于提高空间的利用率同时可以提高组装的效率.匈牙利生物物理学家Tamás Vicsek描述了在原始拓扑正方形上进行的迭代过程,这种分形称为Vicsek分形或盒分形.参考图2,这种分形以一个简单的正方形开始,此时其迭代顺序为零.接下来,将正方形分成九个相等的小正方形,保留拐角的四个正方形和中间正方形或者在拐角处移除四个正方形.重复上述过程进行迭代,如果迭代过程进行无限次,则Vicsek分形图形的周长无限长,但其面积有限.

图2 Vicsek分形的两种形式Fig.2 Tow forms of Vicsek fractal
2.2 任务规划
根据分形理论,以Vicsek分形为基础结构,考虑每个微型航天器都容纳有效载荷(如天线,望远镜镜面),这样问题就转化为航天器集群组装完成分形结构.本研究以125个同构微型航天器为例,将组装过程分为三个阶段,如图3所示.

图3 基于Vicsek分形的航天器在轨组装各阶段构型Fig.3 Configuration of spacecraft in-orbit assembly based on Vicsek fractal: (a)Initial state(125 quantity);(b)First stage(25 groups);(c)Second stage(5 groups);(d)Third stage(final configuration)
对于Vicsek分形天线,理论上天线的周长可以是无限长的(忽略每一小节的天线所占面积),但是在本文提出的航天器组装构型中,航天器的尺寸是无法忽略的,因此有限面积内无限周长的特性并不适用,然而尽管增加航天器的数量后构型占用的面积变大,但是比起天线周长的大幅增加,面积的增加可以说是比较小的.对于Vicsek分形分布式望远镜,每个航天器均为一个小型望远镜,可以利用分布式空间光学干涉技术用多个小型望远镜对同个目标实现高分辨率成像观测,同时由于具有足够多数量的小型望远镜可以对多个目标进行观测,以提高观测效率.如图3(d)所示在构型包络的正方形内,没有被航天器填充的空白区域占比较小,并且航天器设计的尺寸越小同样面积内的填充率就越高,天线周长也越长,所以这种分形构型可以提高空间的利用率.
如图3(a)所示,初始时刻航天器之间相互分离,第一个阶段,每5个航天器为一组,一共分为25组,组内航天器组装为一个形如图3(b)的十字航天器,组装完成的航天器面积为初始微型航天器的5倍,组内以及组和组之间所有航天器的形状保持一致.第二阶段,每5个十字航天器同样按照十字形组装,一共有5组,组装完成形如图3(c)的航天器是由25个初始微型航天器组成的复杂航天器,其面积为上一阶段十字形的5倍,为初始微型航天器的25倍.最后一个阶段,将第二阶段组装完成的5个十字航天器完全组装,此时组装完成形如图3(d)的航天器由起始的125个同构航天器组成,面积仍旧为上一阶段的5倍.因此在航天器组装过程中,每一阶段组装完成的航天器均是十字形,航天器不仅与同一阶段的不同组之间的航天器几何形状相同,同时与不同阶段航天器的几何形状相似,从而可以认为具有分形的自相似性.如果需要增加航天器的数量或增加组装结构面积,可按照这种组装方式无限迭代下去直至完成所有航天器的组装.
2.3 控制力与控制力矩设计
将每一阶段的组装过程分为两个环节,第一个环节为控制追踪航天器使其和目标航天器达到一个较为接近的相对距离并且保持相对静止,称为预组装环节;第二个环节为控制追踪航天器缓慢逼近目标航天器,最后使得两航天器完全对接.以组装的第一阶段为例,组装过程如图4所示.每个组内都有一个航天器认为是目标航天器(红色标出),其余四个航天器为追踪航天器(蓝色标出),追踪航天器均追踪组内的目标航天器.
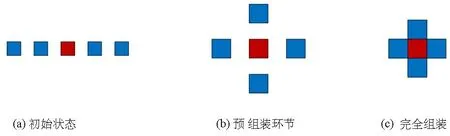
图4 在轨组装过程示意图Fig.4 Schematic diagram of in-orbit assembly:(a)Initial state;(b)Pre-assembly;(c)Assembly
在实际情形下,追踪航天器在逼近期望位置过程中可能会发生与其他航天器等物体的碰撞,因此需要在预组装环节加入避撞力,避免碰撞的发生.fp为基于以下排斥势场负梯度产生的避撞力.
(13)
其中N是针对当前航天器需要将其他航天器考虑为障碍的数量,ri是当前航天器与第i个障碍物的相对距离,d0,i和δ0,i分别代表危险和避撞区域的半径.ki定义为
(14)
因此,基于以上避撞势力场,fp可以设计为

(15)
选用传统的PD控制律加上避撞力的方法对追踪航天器和目标航天器之间的相对位置以及相对姿态进行调节,在本文中将作用在追踪航天器上的主动控制力表示为
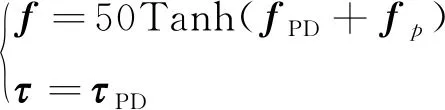
(16)
其中对于任意向量x=[x1,x2,x3]T,Tanh(x)=[tanh(x1),tanh(x2),tanh(x3)]T.由式(15)可知,当不添加任何饱和函数时,避撞力在接近到危险区域半径时,趋向于无穷,但是考虑到作用在航天器上的控制力不能过大,所以为了避免进一步避免碰撞的发生,将预组装环节的固定期望位置用关于时间的一次函数来替代,即
(17)
因此,修正后的PD控制器表示为
(18)

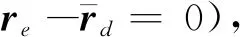
(19)
从上式可以发现一旦‖rei‖小于2m且两个航天器几乎相对静止时,避撞将停止工作,即当‖re1‖<2.5(m)且‖ve1‖<0.005(m/s)时,可以认为两航天器之间已经完成预组装环节,满足进行下一步对接的条件.
3 仿真算例
初始航天器的尺寸均为边长为0.5m的立方体,每一阶段航天器的质量与转动惯量见表1所示.设置系统的初始条件,所有的航天器初始姿态均为[0;0;0],其他初始条件以第一组航天器为例,初始位置、初始速度和角速度见表2所示,其中目标航天器初始位置采用文献[20]中的数据.每往后一组,组内的航天器除了初始位置的x轴+50m以外,其余都保持与上一组相对应的航天器一致,即初始状态下所有航天器等距在x轴上一列排开,每五个航天器为一组并且每个航天器质心与相邻航天器质心的距离均为10m.设计各阶段航天器预组装和完全组装的相对期望位置见表3所示.此外,每一阶段的航天器避撞半径以及控制器增益分别如表4、表5所示.由表1可得三个阶段的航天器的质量以及转动惯量逐阶段增大,且不同阶段避撞力中的危险和避撞半径不一致导致避撞力的变化情况也不一致,因此为了得到比较好的控制效果,比如减少振荡,更平滑地从预组装环节向完全组装环节过渡等,需要调节各阶段追踪航天器的控制器增益.

表1 航天器质量和转动惯量

表2 组内航天器的初始运动状态(第一组)

表3 航天器预组装相对位置和完全组装相对位置

表4 追踪航天器的控制增益

表5 避撞半径
基于选定的初始状态和组装策略,可以得到同一阶段组与组之间的航天器初始相对运动状态以及期望相对运动状态均一致,可以认为各组的组装过程是一个重复任务.
在此初始条件以及控制器参数下的仿真结果如图5~图14所示.其中如图5~图7所示,蓝色实线表示当前阶段下所有追踪航天器与位于中间的航天器的相对位置,红色实线表示当前阶段所有目标航天器与位于中间的航天器的相对位置,由于第一阶段将所有航天器分为25组,因此如图5所示,时间为0s~2000s时一共有25条红线.图7为z轴上航天器之间的相对距离,结合表2可知各组的4号航天器与组内目标航天器在z轴的方向上有初始相对速度,因此在0s附近有一个数值变化.航天器分别在0s,1000s,4500s开启第一阶段,第二阶段和第三阶段,并且分别在200s,1400s,5535s左右在各自的阶段开始从预组装环节向完全组装过渡,即追踪航天器均缓慢地向各自的目标航天器逼近,并且在此过程中无振荡发生.航天器在400s左右完成第一阶段的组装,即125个微型航天器组装成为25个形如图3(b)的十字航天器,约在3200s左右完成第二阶段组装,此时组装结果为5个形如图3(c)的较为复杂的十字航天器,最后在7500s左右组装成为形如图3(d)的航天器,此时认为125个航天器完成所有组装任务.各阶段之间的时间以及第三阶段稳定后的时间也表明了设计的控制器是可以保证航天器到达相对期望位置和姿态后仍能保持收敛.在200s左右,所有航天器的相对姿态以及作用在追踪航天器上的控制力矩均达到了一个很接近0的数并且保持在0附近,因此认为在200s以后所有航天器均保持姿态同步.由于避撞力的加入以及期望相对位置的修正,所有航天器在预组装环节均不会发生碰撞,并且可以较为平滑地向完全组装过渡.
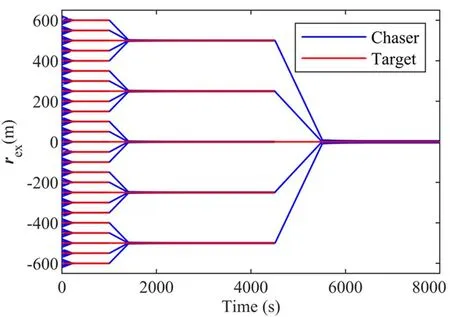
图5 全过程所有目标航天器与追踪航天器的相对位置(x轴)Fig.5 Relative position of all target and chaser spacecraft in the whole mission (x-axis)

图6 全过程所有目标航天器与追踪航天器的相对位置(y轴)Fig.6 Relative position of all target and chaser spacecraft in the whole mission (y-axis)

图8 全过程所有目标航天器与追踪航天器的相对姿态Fig.8 Relative attitude of all target and chaser spacecraft in the whole mission

图9 所有追踪航天器上的控制力Fig.9 Control force acting on all chaser spacecraft

图10 所有追踪航天器上的控制力矩Fig.10 Control torque acting on all chaser spacecraft

图11 航天器相对位置局部放大图(x轴)Fig.11 Local enlarged drawing of relative position of spacecraft(x-axis)
图12~图14为各过程任意一组组内航天器的相对运动轨迹图,图中的圆圈代表目标航天器,因此其坐标为[0;0;0],值得注意的是,圆圈的尺寸和形状不代表航天器的真实尺寸和形状,只是起到展示航天器相对位置的作用.针对图14即第三阶段航天器相对运动轨迹图,在初始相对位置上追踪航天器与目标航天器在y轴的方向上有大约2m的位移,原因是组与组之间的航天器初始在x轴的方向上有一定的相对距离,即不在同一轨道上,因此在不加外力的目标航天器之间会产生一定的相对漂移量,同样漂移量也在图6中4500s(第三阶段开始)左右存在.
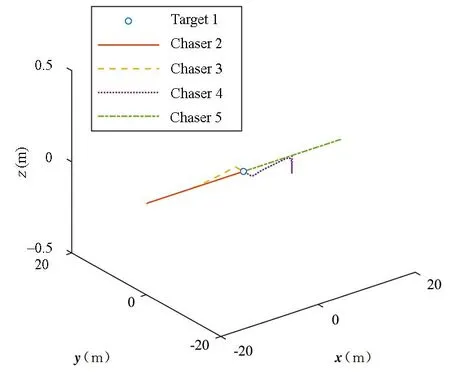
图12 第一阶段任意一组组内航天器相对运动轨迹图Fig.12 The relative motion path of any group of spacecraft in the first stage
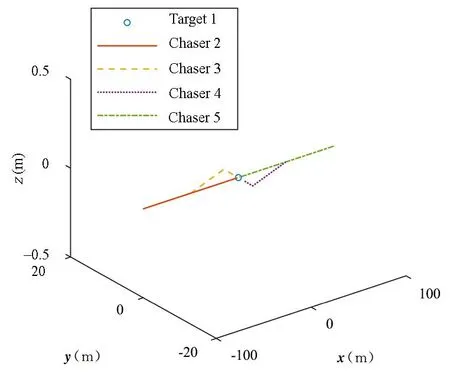
图13 第二阶段任意一组组内航天器相对运动轨迹图Fig.13 The relative motion path of any group of spacecraft in the second stage
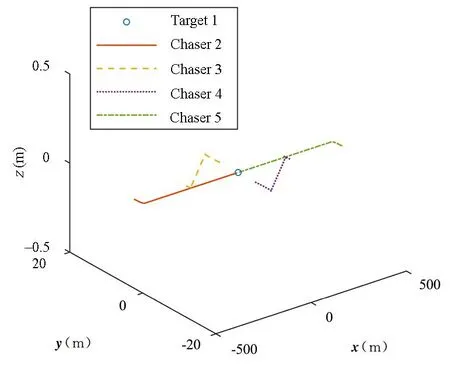
图14 第三阶段航天器相对运动轨迹图Fig.14 The relative motion path of spacecraft in the third stage
4 结论
针对刚性航天器在轨组装的构型以及动力学与控制问题,本文基于Vicsek分形结构设计了一种航天器的组装构型以提高组装效率,同时发挥分形结构可无限迭代的特点来提高空间的利用率,将125个同构航天器组装过程分为三个阶段,每个阶段的构型均满足分形的自相似性.建立了刚性航天器的位置和姿态动力学方程并导出追踪航天器与目标航天器的相对参数,为了完成航天器的组装并且在组装过程中避免碰撞,每个阶段均分为预组装环节和完全组装环节,其中预组装环节选用避撞复合PD控制器,在完全组装环节仅采用PD控制.仿真结果表明:本文对航天器在轨组装的任务规划是合理的,以及针对组装任务设计的控制器可以有效避免碰撞的发生,并且能保证所有航天器姿态同步,最后完成125个航天器的组装.
