云环境下实现容器部署的加速粒子群优化算法

陆海锋 赵嘉凌 欧阳学名 周娜琴 左利云

摘 要：基于容器的微服务部署是一个具有挑战性的问题，为获得更好的用户体验并给云供应商带来更多的利润，需要在降低微服务的故障率和减少响应时间的同时提高资源利用率。提出了一种改进的加速粒子群优化算法，用于解决集群中微服务容器部署的多目标优化问题。该算法通过考虑微服务之间的调用关系，使得容器聚集在一起，从而降低服务的数据传输成本、减少故障率，并提高集群资源利用率。与现有部署算法相比，实验结果表明，所提出的优化算法在服务间的数据传输开销、故障率和资源利用率等性能指标上有明显改善。具体表现在：容器聚集度的提升达到40%以上，数据传输消耗平均有提升4%以上，故障率减少10%～20%，利用率提升3%左右。

关键词：云计算； 微服务； 容器； 加速粒子群算法； 多目标优化

中图分类号：TP393.09   文献标志码：A

文章编号：1001-3695（2024）03-016-0756-08

doi：10.19734/j.issn.1001-3695.2023.07.0312

Accelerated particle swarm optimization algorithm forcontainer deployment in cloud environments

Lu Haifeng1， Zhao Jialing1， Ouyang Xueming2， Zhou Naqin3， Zuo Liyun4

（1.Information Center Dept.， Zhaoqing University， Zhaoqing Guangdong 526061， China; 2.School of Software， South China University of Technology， Guangzhou 510006， China; 3.Cyberspace Institute of Advanced technology， Guangzhou University， Guangzhou 510006， China; 4.School of Computer Science， Guangdong University of Petrochemical Technology， Maoming Guangdong 525000， China）

Abstract：Container-based microservice deployment is a challenging problem that aims to improve user experience and increase cloud providers profitability by reducing microservice failure rates and response times while maximizing resource utilization. This paper presented an enhanced accelerated particle swarm optimization algorithm to tackle the multi-objective optimization problem of microservice container deployment in a cluster. By considering the invocation relationships between microservices， the algorithm facilitated the aggregation of containers， thereby reducing data transmission costs， lowering failure rates， and enhancing cluster resource utilization. Experimental results demonstrate that the proposed optimization algorithm yields significant improvements in performance measures including data transmission overhead， failure rate， and resource utilization when compared to existing deployment algorithms. Specifically， the algorithm achieves a container aggregation improvement exceeding 40%， an average increase in data transmission consumption of over 4%， a decrease in failure rate by 10% to 20%， and an increase in utilization rate by roughly 3%. The aforementioned findings attest to the efficacy of the proposed algorithm.

Key words：cloud computing; microservices; container; accelerated particle swarm optimization; multi-objective optimization

0 引言

在云環境中，计算资源通常以虚拟机（VM）或容器的方式提供各种计算服务，而应用程序则采用微服务架构模式来向用户提供服务［1～3］。

微服务架构已被广泛应用于云应用系统的构建和部署。与传统的单体式应用不同，微服务架构采用强解耦的方式将单体应用程序拆分成一组小粒度的服务，这些服务通常以VM和容器的形式分布在云数据中心（CDC）中。这些服务通过轻量级的通信方式进行交互，并通过组合构建应用系统［4］。用户可以通过云平台提供的操作来部署应用系统，而这些应用系统通过基于容器的调度引擎协调使用CDC的计算资源并进行交互。

基于容器的微服务部署和资源管理是一个重要问题。微服务架构已成为云计算领域的主导趋势，将单块应用程序拆分为多个面向场景的服务块（微服务）。拆分过程导致高度动态的执行场景，在这个场景中，各种串行的微服务以不同的方式竞争计算资源［5］。目前，基于操作系统级别容器的部署方法，如Linux容器（LXC）和Docker等，已成为微服务部署的主流技术。与虚拟机不同，这种容器是一种更轻量级的虚拟化方法，具有较少的计算和存储资源需求，更短的启动时间。容器使用命名空间来打包系统的计算資源，使得微服务的部署和扩展变得更加容易［6］。通过调整服务器和网络资源来适应集群中工作负载的快速变化，以缓解资源耗尽或满足服务性能的要求，Valsamas等人［7］研究了一种新的云编排策略，称为虚拟化技术混合（VTB）。VTB考虑支持替代虚拟化选项的边缘云，包括多类型、相同或类似服务的容器构建，方便它们有效地混合使用，以处理具有挑战性资源需求的情况——具有不同的资源需求和性能能力，研究团队还提供了一个相关的优化框架，所提出的策略可增加服务的用户数量，并能有效提高服务器和网络资源的利用率。然而，构建高效的微服务部署和资源管理算法需要综合考虑用户的体验质量和云提供商的利润，例如降低微服务的响应时间和故障率，提高集群的资源利用率。为解决这一问题，本文通过优化服务间的平均数据传输开销、执行故障率和集群的资源利用率，以实现用户和云提供商间的利益平衡。在微服务部署过程中，根据微服务之间的调用关系进行容器实例的部署，微服务通过调用关系进行组合构建服务功能链（SFC）［8］。然后，将SFC中的微服务容器实例尽可能聚集在同一计算服务器节点或CDC中，以降低服务间的数据传输成本和提高集群资源利用率，同时考虑服务执行的可靠性问题。

本文的主要贡献如下：

a）确定了微服务部署的优化目标，包括执行容器聚集、服务间数据传输开销、服务执行故障率和集群资源利用率。针对这些优化目标，构建了一个多目标优化问题。

b）提出了一种改进的加速粒子群优化算法来解决微服务容器部署的多目标优化问题。该算法利用适应度函数值选择全局最优解，并通过调整粒子的速度和位置来搜索最优解空间。

c）通过实验结果表明，与其他算法相比，该算法在数据传输成本、故障率和资源利用率等性能指标上取得了显著的改进，证明了该算法的可行性和有效性。

1 相关研究

微服务实例部署和CDC资源利用是IoT云环境中至关重要的问题，它直接影响到最终用户和云服务提供商之间的利益平衡。CDC资源管理优化是研究者们关注的热点问题。目前已有多种相关的服务部署策略和调度方法：

首先，在云环境下，研究者倾向于采用元启发策略来解决多目标优化问题，以获得最优解（即Pareto解）。使用元启发策略的主要原因在于它是一种随机算法，具有不确定性的特点，并且不受优化问题的数学性质的限制。此外，群体中的个体通过协作可以更好地适应环境和相互交互，有更多机会获得全局最优解。例如，Liu等人［9］提出了一种进化博弈算法优化IoT环境中的服务组合和部署。Gao等人［10］为解决QoS和鲁棒性的双目标服务组合和优化选择（BoSCOS）问题，构建了两个准则及其数学模型，并提出了一种增强多目标灰狼优化器（SMOGWO）来高效解决上述模型。为优化容器的分配和弹性管理，Ahmad等人［6］提出了一种非支配排序遗传算法-Ⅱ（GA-NSGA-Ⅱ），该算法能解决云集群、容器、微服务等云架构中的资源管理优化问题，并在系统供应、系统性能、系统故障和网络开销方面获得明显的改善和提高。Zhao等人［11］提出了一种基于历史经验引导的信息素更新策略的蚁群优化算法，以提高云中的微服务部署与资源管理效率和增强优化，并通过学习自动机根据搜索历史自适应地选择适合的信息素更新方法。为完成无人机的任务卸载，Mousa等人［12］针对该混合整数非线性约束优化问题，提出了一种采用新的变异和交叉操作符的离散差分进化算法，并应用蚁群优化（ACO）算法来寻找无人机在集群头部之间遍历的最短路径。针对在不同资源中心部署和启动微服务实例的问题，Ma等人［13］提出了一个基于进化多目标理论的优化问题模型，并用一种知识驱动的进化算法（NSGA-Ⅲ）来解决该问题模型，寻找不同资源中心微服务实例的最优部署和启动策略。

随着任务或请求规模的增加和云资源的动态性，负载平衡、资源利用率、任务分配和系统性能等问题变得越来越突出。由于粒子群优化算法在多目标优化问题中的有效性，研究者们已将其应用于云环境中的优化策略。与传统优化方法相比，元启发式算法在解决微服务部署这类多目标优化问题时具有独特的优势，能够降低问题的复杂性，广泛应用于云环境中的多目标组合优化问题中。在各种元启发式算法中，粒子群优化（PSO）是一种著名的元启发式技术，用于解决优化问题。PSO适用于动态任务调度、工作流调度和负载平衡。PSO在运行开始时具有很强的全局搜索能力，并在运行接近结束时进行局部搜索［14］。元启发式算法包括加速粒子群优化（APSO）、进化博弈策略、灰狼算法（WA）、遗传算法（GA）、蜜蜂算法（HBA）、蚁群优化（ACO）和人工鱼群算法（AF）等。其中，APSO是粒子群优化算法的改进版，通过使用群体的全局最优解来促进算法的收敛性和随机性［15］。本文针对优化服务间的数据传输开销、执行部分和集群资源利用率，提出了一种改进的加速粒子群优化算法，用于解决微服务容器部署的多目标优化问题。

随机初始化搜索解是其中的一个关键特征。然而，提供有效的初始化解可以显著提高启发式算法的性能。Alsaidy等人［16］提出了一种改进的粒子群优化初始化方法，利用启发式算法进行初始化，采用最长作业优先到最快处理器（LJFP）和最小完成时间（MCT）算法来初始化PSO，该团队提出的LJFP-PSO和MCT-PSO算法的性能通过最小化完成时间、总执行时间、不平衡度和总能耗指标进行评估。在解决云计算中的任务调度问题时，Dubey等人［17］提出了一种新颖的混合任务调度算法——化学反应部分粒子群优化（CR-PSO），可以在可用虚拟机上分配多个独立任务。该算法增强了传统的化学反应优化和部分粒子群优化，并通过结合特征进行混合化，以找到最佳的任务调度顺序，使得任务可以基于需求和截止时间同时进行处理，以改善成本、能量和完成时间等因素的质量。

与前述工作不同，本文的优化目标包括服务间的数据传输开销、执行故障率和微服务容器聚集值，并采用加速粒子群优化算法（APSO）解决服務容器部署问题。本文提出的部署策略通过服务间的调用关系，将服务功能链中服务的执行容器进行聚集，以降低服务的数据传输成本、执行故障率，并提高CDC的资源利用率。改进的加速粒子群优化算法（APSO-CDSM）用于解决基于微服务容器部署的多目标优化问题，其优越性主要体现在：

a）APSO-CDSM算法能有效地解决多目标优化问题，通过使用APSO算法进行优化，可以快速有效地找到微服务容器部署中的三个性能指标（服务间数据传输开销、执行部分和集群资源利用率）的近似最优解，从而提高系统的性能和效率。

b）改进PSO算法。APSO-CDSM是PSO算法的改进版，通过利用群体的全局最优解来促进算法的收敛性和随机性。这种改进使得APSO-CDSM算法在运行初期具有很强的全局搜索能力，有助于找到全局最优解；同时在运行接近结束时，算法会进行局部搜索，进一步优化解的质量，能有效地提高全局搜索和局部搜索能力。这种全局搜索和局部搜索能力使APSO-CDSM算法在解决复杂问题时具备较好的收敛性和随机性，更适用于解决复杂的多目标优化问题，并且在算法性能方面可能具有更好的表现。

2 容器部署建模及目标模型

2.1 容器部署模型形式化描述

云平台中，用户可通过平台提供的操作来部署应用程序。基于容器的调度引擎根据微服务接收的用户请求数和所需资源数，寻找合适的计算服务器来部署服务容器。为了实现用户和云提供商之间的利益平衡，即减少服务执行的响应时间和降低故障率，并提高集群的资源利用率，本文提出将同一服务功能链（SFC）中的微服务容器尽量聚集到同一个服务器节点或同一容器数据中心（CDC）。

设Users={userv|1≤v≤V}为用户集，userv=〈ureqsv，uposv〉且v∈{V}，其中，ureqsv为用户请求应用程序的次数，用户所在的位置uposv=〈posx，posy〉。Apps={appc|1≤c≤C}表示应用程序集， appc=〈ureqsc，SFCc〉且c∈{C}。SFCc=〈MSsc，Edsc〉表示应用程序的服务功能链SFC，MSsc={MSi|1≤i≤I}。MSi=〈Msreqi，ReqsCPUi，ReqsStorei，ReqThri〉，其中，Msreqi表示请求服务MSi的次数；ReqsCPUi和ReqsStorei分别表示请求/调用服务MSi一次所需的CPU和存储资源量；ReqThri表示请求/调用服务的最大次数（阈值）。

在CDC中，设PMs={pmj|1≤j≤M}为计算服务器集群。pmj=〈pmCPUj，pmStorej，pmposj〉。其中，pmCPUj、pmStorej分别为服务器的CPU资源和存储资源；pmposj=〈pmxj，pmyj〉为服务器所在的位置。

令alloc（MSi）≡conk（k≥1）表示服务MSi被封装在容器conk中执行，当TReqsi=ureqsc×Msreqi≥ReqThri时，则需扩展容器实例以平衡负载；那么，容器实例扩展数量为Cinsi=［TReqsiReqThri］=［ureqsc×MsreqiReqThri］。在此，alloc（conk）≡pmj表示容器conk部署在服务器节点pmj，可允许多个容器实例部署在每个服务器中。由上述可知，I个微服务的容器实例部署在M个服务器节点可表示为［xij］I×M，xij=1表示微服务MSi的容器实例部署在节点pmj，否则表示未部署。

2.2 模型目标函数

在此，根据容器部署模型目标可以建立以下三个目标函数，分别为：服务间的数据传输开销、执行故障率、集群的资源率以及微服务容器聚集。

2.2.1 服务间的数据传输时耗函数

CDC的集群通过高速网络进行连接，噪声干扰可被忽略。那么，影响服务间的数据传输开销的因素有：容器镜像大小IMSi、部署容器的服务器间的网络距离Djj′、服务间的请求次数Msreqii′和传输数据量TDii′。由于一个微服务的容器实例可部署到多个计算服务器中，为此，在计算服务间的数据传输开销时采用服务间的多个容器对的数据传输时耗的平均值，如式（1）所示。

其中：X是多目标优化问题的决策向量。式（9）～（11）是优化目标函数。式（12）～（16）是多目标优化问题的约束条件，分别是：a）ReqsCPUixij≤pmCPUj表示CPU资源能满足微服务对CPU的需求约束；b）ReqsStoreixij≤pmSorej表示服务器节点的存储或RAM能满足微服务对存储或RAM的需求；c）TReqsixij≤ReqThri表示确保用户的微服务请求数量小于系统最大阈值，以确保请求能获得响应；d）∑Mi=1xij=1确保至少有一个容器实例能满足微服务的部署要求；e）∑Mj=1xij≥1是资源竞争互斥条件，确保同一微服务对应的容器只有一个且仅有一个能部署到同一个物理服务器内，避免因容器间的资源竞争而造成死锁。

由上述的问题描述模型可知，该多目标优化问题是一个NP-hard问题，主要以计算和存储资源量和请求阈值作为约束，同时优化服务间的数据传输开销、容器聚集值和故障率等目标函数。由于元启发式算法在求解多目标优化问题的优越性，所以本文采用加速粒子群优化算法（APSO）来解决该多目标优化问题。APSO主要通过对粒子的位置和速度进行改进来降低随机性，从而实现Pareto解集的最优解的快速收敛。

3 目标函数求解——加速粒子群优化算法

3.1 APSO算法

粒子群优化算法（PSO）是一种通过模拟鸟群觅食的智能群体优化算法。该算法的核心思想是：在鸟群觅食过程中，个体为了寻找到食物目标需在搜索空间中不断调整自身的飞行轨迹。改变飞行轨迹包括自身经验和全体经验两个因素。自身经验是一种局部最优（personal best，Pb），即个体最优位置；而全体经验是一种全局最优（global best，Gb），即群体中的最优位置。然后，群体中的个体通过不断改变自身位置和速度来逼近最优目标，从而实现寻优目标。为了提升粒子群优化算法的全局最优解的收敛速度，提出一种改进版的PSO，即加速粒子群优化（APSO）算法。APSO算法是采用全局最优来更新速度。假设在N维搜索空间中，粒子群为Pops={pi|1≤i≤P}，pi=〈Xi，Vi〉，其中，Xi={Xni|1≤n≤N}是粒子的位置向量，Vi={Vni|1≤n≤N}是粒子的速度向量。对于t（t为某一时刻或迭代次数），粒子pi的速度和位置更新公式分别如式（17）和（18）所示。

Xi（t+1）=Vi（t+1）+（1-σ）Xi（t）（18）

其中：σ∈［0.1，0.7］；ρ∈［0.1，0.5］L，L是变量刻度；ε∈rand（0，1）为随机向量，其值为0～1；Gb*为全局最优。

3.2 粒子编码

APSO算法关键问题之一在于解决粒子编码，每个粒子个体都倾向于实现优化目标以获得更好的值；并且在个体寻优过程中，需不断地调整位置和速度，以便生成新的解。根据第2章建立的优化问题，使用字符串对个体进行编码，即采用数组的方式来表达粒子，数组的每个元素对应一个微服务，序列号为微服务ID，粒子pi（1≤i≤P）的结构如表1所示，包含了I个微服务。在表1中，服务器节点列表是部署微服务容器的节点ID，每个节点ID只出现一次，这是基于式（11）的约束，主要是为了避免因争夺资源而发生冲突，所以约定同一微服务在同一服务器只部署一个容器实例。

在服务器节点列表中，每个节点ID采用0-1编码表示。令集群中总共有M=240个服务器节点，节点ID的编码长度nID=［log2M］，对应的0-1编码为［11110000］。服务器节点进行如下的设置编码，如MS1的服务器节点列表为XMS1={［00000111］，［00001001］，［00100001］}。基于此，Xk=（XMS1，XMS2，…，XMSI）为粒子pi的位置，即为优化问题的一个解。

由上述粒子的位置可知，其值在0～1变动，本文使用sigmoid函数来刻画0～1的變换速度vt。

sigmoid（vt）=11+evt（19）

x=1 若rand＜sigmoid（vt）0 else（20）

那么，对于任意t，分别对粒子pi的速度和位置更新公式进行改进，如式（21）和（22）所示。

Vi（t+1）=Vi（t）+σ（x*n（t）-xn（t））+ρ*rand（1，nID）（21）

xi（t+1）=1 若rand＜sigmoid（vt）0 else（22）

其中：n∈{nID}；x*n是全局最优粒子的位置状态。

3.3 适应度函数

针对第2章提出的多目标优化问题，为了获得问题模型的次优解或最优解，本文采用APSO算法来实现微服务的容器部署，即将微服务对应的多个容器实例部署到合适的计算服务器。在部署过程中，每个粒子pi的位置Xi都是问题的解。在此，本文采用适应度值来评估每个位置Xi，通过归一化方法将三个优化目标函数聚合到一个评估函数中，其公式如式（23）所示。

Fitness（X）=γ1Trans（X）-TransminTransmax-Transmin+

γ2CAV（X）-CAVminCAVmax-CAVmin+γ3MSF（X）-MSFminSEFmax-MSFmin（23）

其中：0≤γi≤1且∑3i=1γi=1，γi可根据实际业务需求进行调整；Transmin、CAVmin、MSFmin是目标值的最小值，Transmax、CAVmax、MSFmax是最大值。

在任意t，首先基于支配关系可选择出非支配解集，即Pareto集（归档集）；然后采用拥挤距离计算非支配解到全局最优之间的距离；最后从Pareto集中选出拥挤距离最小且适应度值最小的粒子更新全局最优，使得群体不断向最优解逼近。

3.4 算法过程描述

APSO-CDSM算法的服务容器部署流程如图1所示。

APSO-CDSM算法的寻优步骤如下：

a）初始化。该算法生成粒子群Pops={pi|1≤i≤P}，包括初始位置X、速度V以及初始化参数σ、ρ。

b）迭代过程。

（a）评估每个个体pi的适应度函数值，基于拥挤距离选择归档集Arc。

（b）从Arc中选择最优个体Gb*。

（c）个体速度Vi和位置Xi的更新。

（d）为微服务MSk寻找合适的服务器节点，若资源剩余量满足资源请求量，则分配对应的容器coni到服务器节点pmj；否则，寻找下一节点。循环执行Cinsk次，直到所有容器被部署。继续迭代步骤（a）。

c）迭代结束。当所有微服务容器部署到合适的服务器节点，则完成一次迭代。

d）若达到最大迭代次数，则结束算法。

算法1 APSO-CDSM算法伪代码

输入：P，nID，σ，ρ，Iters;MSs={MSk|1≤k≤I};MS_Rs={（MSk，MSk′，Rs）|MSk，MSk′∈MSs，Rs∈MR};PMs={pmj|1≤j≤M}。

输出：Ms_PMs={（Msk，PMj）|PMjPMs}。 /*为每个微服务找到合适的服务器节点集*/

t←1；

Pops←iniPops（P）;

fitness←Galfit（Pops）;

Arc←Deter min e（Pops）;

while（t≤Iters）do

Gb←ChooseGb（Arc，fitness）;

for each pi do

for MSk do

While l≤Cinsk do

While（true）do

for n≤nID do

update vcn by 式（21）;

update xcn by 式（22）;

end for

if（ReqsCPUk≤ReCPUj∧ReqsStorek≤ReStorej）

update MS_PMs by （k，j）;

break;

end if

end while

end while

end for

end for

fit←Calfit（Pops）;

Arc←Deter min e（Pops）;

end while

return Ms_PMs

4 实验结果分析与对比

为了评估APSO-CDSM算法的性能及有效性，解决2.3节中所提出的在式（12）～（16）约束下的多目标优化问题模型，在优化对应的三个性能指标中体现出全局搜索和局部搜索的提升能力，本文实验采用阿里云提供的跟踪V2018［19］数据集。

4.1 实验数据及参数设置

在实验中，基于跟踪V2018数据集的分析，考虑了一个应用程序，存在三个SFC（SFC1，SFC2，SFC3），包含18个微服务，每个服务的基本信息以及服务间的调用关系信息如表2和图2所示。在表2中，SFC、ReqsCPUk、ReqsStorek分别表示微服务所在的SFC、所需的计算和存储资源；Msreqk、ReqThrk、Cinsk分别表示请求微服务的次数、阈值以及容器实例数；IMSk、IMOk分别表示容器镜像大小及传输开销。

图2为微服务间的调用DAG，图中的三元组表示的权值分别是：weight表示SFC中微服务间边的权值，weight表達了边的不同调用关系，边权值越大，说明两个微服务间的数据交互越紧密；Msreqkk′、TDkk′分别表示服务间的请求次数和数据传输量。此外，（0，MSk）表示客户端启动服务MSk。

异构CDC中的集群参数设置如表3所示。

表3中，Djj′=1.0、4.0和8.0分别表示同一节点、同一CDC以及不同的CDC。表4是APSO-CDSM算法的参数设置。

实验环境：处理器为AMD A6-6310 APU with AMD Radeon R4 Graphics 1.80 GHz， 内存为8 GB RAM。

为了验证APSO-CDSM算法的性能和有效性，本文将其与GA-NSGAⅡ［12，20，21］、ACO-MCMSA［22］和MSG-NSGAⅢ［13，23］算法进行对比。在实验中，采用MATLAB工具构建了测试代码，并分别对两种集群规模（M=［120，240］）施加六种请求数ureqs={×1.0，×2.0，×3.0，×4.0，×5.0，×6.0}。为获得准确有效的实验数据，每种设置下各完成20次实验，最后对实验结果进行统计分析与比较。

4.2 结果分析与对比

采用阿里云提供的V2018数据集，通过两个模拟实验来验证APSO-CDSM算法的性能，并与现有的GA-NSGAⅡ、ACO-MCMSA和MSGA-NSGAⅢ算法进行性能比较。在实验中，实验1和实验2的集群规模分别设定为M=128/256，考察的性能参数有微服务容器聚集值、服务间的数据传输开销、故障率以及集群的资源利用率等。

4.2.1 微服务容器聚集度CAV

四个算法的微服务容器聚集值对比情况如图3～5所示。通过其值范围来考察容器聚集对服务间的数据开销和集群资源利用率的影响。

图3是针对实验1（M=128）中获得的容器聚集值的平均结果统计数据对比折线图，以及在对应六种请求数情况下APSO-CDSM算法对比其他三个算法的提升百分比分布情况盒图。由图3可知，APSO-CDSM算法获得的容器聚集值对应的折线是最底下的折线，是对比算法中最好的，同时其提升都大于13.4%，而且在第一种请求数情况下表现得最稳定，其提升分布大于55%，最大提升相对于MSGA-NSGAⅢ达到76%以上。针对实验1，APSO-CDSM算法整体提升平均达到42.2%。

同样，针对实验2的配置（M=256），验证APSO-CDSM算法对比其他算法获得的容器聚集值的数据情况的统计如图4所示。由图4可以看到，APSO-CDSM算法对比其他三种算法，在容器聚集的平均值上提升的百分比最少为28.4%，最大达到了82.4%，总体平均提升56.9%。

綜合针对集群规模分别为M=128和M=256的两个实验，各个算法获得的容器聚集度的分布如表5所示。

对应的两个实验获得的结果箱图及对应的平均取值折线图如图5所示。由图5可知，两个不同集群规模实验结果中，APSO-CDSM算法获得的数据要比其他三个算法更好，特别是集群规模变大时（M=256时），其获得容器聚集值较对比算法更好更稳定。这点由各次实验统计的容器聚集值的平均值取值区域在0.021 8～0.030 8，均小于其余算法的平均值可知。APSO-CDSM算法的整体效果也是最好的。

4.2.2 服务间的数据传输消耗Trans

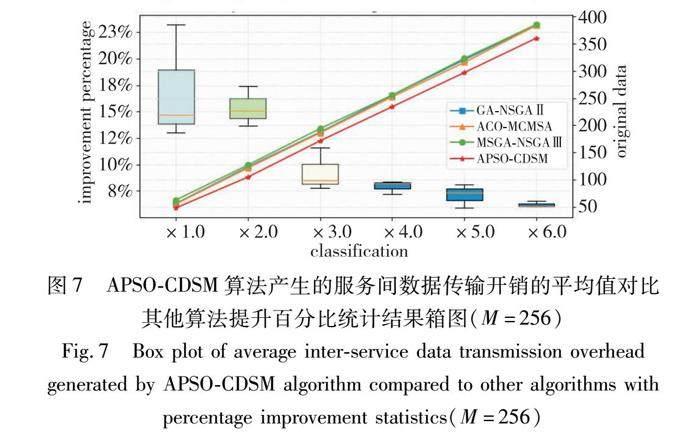
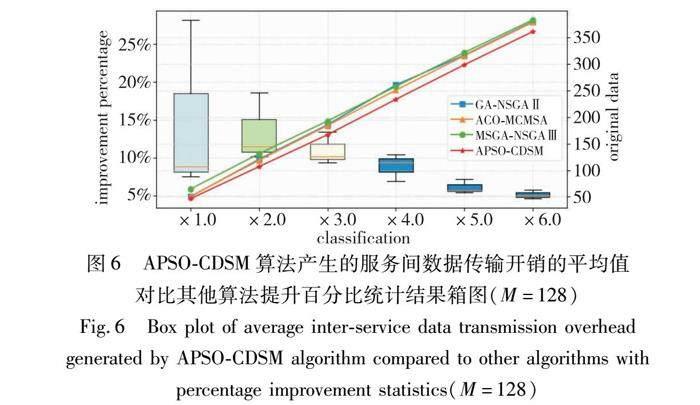
服务间的数据传输开销是指多个容器对的数据传输开销的平均值。在上述两个实验中，统计两个实验采用不同算法得到的各个服务间数据传输消耗的平均值结果如图6～8所示。

图6、7分别是集群规模M=128和M=256环境下，APSO-CDSM算法产生的服务间数据传输时耗的平均值对比其他算法，在不同请求数下提升百分比统计结果箱图。图中的折线是不同请求数下各算法获得的服务间数据传输开销的平均值。

综合两个集群规模各个算法在所有实验中得到的服务间数据传输开销的平均值，其统计结果如图8所示。

图8 服务间数据传输开销平均值统计箱图及平均值折线图

Fig.8 Box plot and mean line graph for average inter-service datatransmission overhead statistics

由图8两个子图对应的箱图结果可知，APSO-CDSM算法产生的服务间数据传输开销的平均值分布明显处于其他三个算法得到的数据分布的左边，说明其效果是对比算法中最优的。

4.2.3 故障率MSF

在不同环境下还需统计出用不同算法对资源进行调度触及服务执行发生的故障平均率，以反映不同算法在资源调度中的有效性。服务执行发生故障会影响调度的整体性能，包括资源利用率、服务响应时间等。统计两种集群状态下不同算法获得的服务执行发生故障率的平均值，按故障率平均值的大小生成相应的热力图，同时将APSO-CDSM算法得到的故障率对比其他三种算法，计算其效果提升情况的百分数分布的箱图，最后得到四个子图的数据可视化图，如图9所示。热力图颜色越浅表示对应算法下的故障率均值越小，APSO-CDSM算法对应行所有格子的填充色是所在列中最浅的，同时由其提升百分数分布箱子可看到：在M=128情况下至少提升3%左右，最大达到 28%；M=256时，效果提升稳定在10%～20%。其故障率也在四种算法中获得了最好的效果。

4.2.4 集群资源利用率AR

好的调度策略和算法能充分利用集群中各类核心资源，让资源的利用率得到更大提升。实验统计了不同集群参数和不同的请求数需求下服务器中CPU和RAM两类核心资源的利用率。图10、11分别展示了在M=128和M=256集群规模下不同算法的CPU和RAM利用率的热力图。

核心资源利用是衡量调度算法的优劣指标之一，集群内资源利用率越高，表示算法能充分利用资源，更好地提升集群的性能。图10、11中颜色越深表示对应资源的利用率越高，观察四个子图，其中APSO-CDSM算法对应行的所有格子的填充色相对于同列其他算法都呈现出更深的颜色，表示APSO-CDSM算法对资源的利用率更高，也说明了该算法的优越性。统计所有实验中各算法在CPU和RAM上的利用率，如表6所示。

汇总所有实验中各个算法获得集群资源（CPU和RAM）的平均利用率得到表6的数据可知，相比其他三个算法，应用APSO-CDSM算法的微服务调度能更充分地利用集群资源，其CPU和RAM的利用率是四种算法中最高的。

通过对比四种算法的微服务调度，APSO-CDSM算法在容器聚集度CAV、数据传输消耗Trans、故障率MSF和集群资源利用率AR四个维度上都获得了最优的效果，能作为基于容器的微服务部署和资源管理管理系统的决策引擎，为CDC提供相应部署调度服务。

5 结束语

为解决云数据中心（CDC）中基于容器的微服务部署和资源管理，实现资源有效调度的优化问题，提出一种改进的加速粒子群优化算法，用于解决CDC集群中微服务容器部署的多目标优化问题。该算法通过考虑微服务之间的调用关系，使得容器聚集在一起，从而降低服务的数据传输成本和故障率，并提高集群资源利用率。通过实验，与当前提出的基于容器微服务的部署算法相比，实验结果证明了本文提出的APSO-CDSM算法的有效性和优越性。在四个重要性能指标：容器聚集度CAV，数据传输消耗Trans、故障率MSF和集群资源利用率AR都具有明显的改善和提高，其中，容器聚集度CAV的提升达到40%以上，数据传输消耗Trans的提升平均有4%以上，故障率MSF也减少了10%～20%，利用率提升了3%左右。实验结果表明，APSO-CDSM优化算法能提升和改善集群容器部署的能力，为CDC在容器部署过程中提供决策支持。在今后的研究中，将进一步研究扩展粒子群加速优化算法在CDC和云边端资源调度的应用，为降低能耗和服务部署成本提供更有效的解决方案。

参考文献：

［1］Hwang J， Nkenyereye L， Sung N， et al. IoT service slicing and task offloading for edge computing［J］. IEEE Internet of Things Journal， 2021，8（14）： 11526-11547.

［2］Pham V N， Hossain M D， Lee G W， et al. Efficient data delivery scheme for large-scale microservices in distributed cloud environment［J］. Applied Sciences， 2023，13（2）： 886.

［3］Liu Zheng， Yu Huiqun， Fan Guisheng， et al. Reliability modelling and optimization for microservice-based cloud application using multi-agent system［J］. IET Communications， 2022，16（10）： 1182-1199.

［4］Assun?ao W K G， Krüger J， Mosser S， et al. How do microservices evolve？An empirical analysis of changes in open-source microservice repositories［J］. Journal of Systems and Software， 2023，204：111788.

［5］Wang Xinkai， Li Chao， Zhang Lu， et al. Exploring efficient microservice level parallelism［C］//Proc of IEEE International Parallel and Distributed Processing Symposium. Piscataway，NJ：IEEE Press， 2022： 223-233.

［6］Ahmad I， AlFailakawi M G， AlMutawa A， et al. Container scheduling techniques： a survey and assessment［J］. Journal of King Saud University-Computer and Information Sciences， 2022，34（7）： 3934-3947.

［7］Valsamas P， Skaperas S， Mamatas L， et al. Virtualization technology blending for resource-efficient edge clouds［J］. Computer Networks， 2023，225：109646.

［8］Mostafavi S， Hakami V， Sanaei M. Quality of service provisioning in network function virtualization： a survey［J］. Computing， 2021，103： 917-991.

［9］Liu Dongqing， Hafid A， Khoukhi L. Workload balancing in mobile edge computing for Internet of Things： a population game approach［J］. IEEE Trans on Network Science and Engineering， 2022，9（3）： 1726-1739.

［10］Gao Yifan， Yang Bo， Wang Shilong， et al. Bi-objective service composition and optimal selection for cloud manufacturing with QoS and robustness criteria［J］. Applied Soft Computing， 2022，128： 109530.

［11］Zhao Haitong， Zhang Changsheng. An ant colony optimization algorithm with evolutionary experience-guided pheromone updating strategies for multi-objective optimization［J］. Expert Systems with Applications， 2022，201： 117151.

［12］Mousa M H， Hussein M K. Efficient UAV-based mobile edge computing using differential evolution and ant colony optimization［J］. PeerJ Computer Science， 2022， 8： e870.

［13］Ma Wubin， Wang Rui， Gu Yuanlin， et al. Multi-objective microservice deployment optimization via a knowledge-driven evolutionary algorithm［J］. Complex & Intelligent Systems， 2021，7： 1153-1171.

［14］Pradhan A， Bisoy S K， Das A. A survey on PSO based meta-heuristic scheduling mechanism in cloud computing environment［J］. Journal of King Saud University-Computer and Information Sciences， 2022，34（8）： 4888-4901.

［15］Nouri N A， Aliouat Z， Naouri A， et al. Accelerated PSO algorithm applied to clients coverage and routers connectivity in wireless mesh networks［J］. Journal of Ambient Intelligence and Humanized Computing， 2023，14（1）： 207-221.

［16］Alsaidy S A， Abbood A D， Sahib M A. Heuristic initialization of PSO task scheduling algorithm in cloud computing［J］. Journal of King Saud University-Computer and Information Sciences， 2022，34（6）： 2370-2382.

［17］Dubey K， Sharma S C. A novel multi-objective CR-PSO task scheduling algorithm with deadline constraint in cloud computing［J］. Sustainable Computing： Informatics and Systems， 2021，32： 100605.

［18］Filip I D， Pop F， Serbanescu C， et al. Microservices scheduling model over heterogeneous cloud-edge environments as support for IoT applications［J］. IEEE Internet of Things Journal， 2018，5（4）： 2672-2681.

［19］Zhu Jianyong， Lu Bin， Yu Xiaoqiang， et al. An approach to workload generation for cloud benchmarking： a view from Alibaba trace［C］//Proc of the 15th IEEE International Symposium on Autonomous Decentralized System. Piscataway，NJ：IEEE Press， 2023： 1-8.

［20］Guerrero C， Lera I， Juiz C. Genetic algorithm for multi-objective optimization of container allocation in cloud architecture［J］. Journal of Grid Computing， 2018，16： 113-135.

［21］吳祥， 董辉， 俞立，等. 多色服装裁剪分床计划复合优化算法［J］. 控制与决策， 2022，37（6）： 1531-1540. （Wu Xiang， Dong Hui， Yu Li， et al. Hybrid optimization algorithm for cut order planning of multicolor garment［J］. Control and Decision， 2022，37（6）： 1531-1540.）

［22］Lin Miao， Xi Jianqing， Bai Weihua， et al. Ant colony algorithm for multi-objective optimization of container-based microservice scheduling in cloud［J］. IEEE Access， 2019，7： 83088-83100.

［23］张珊莉， 谢加良， 陈水利. 基于模糊系统的改进型NSGA-Ⅲ算法［J］. 模糊系统与数学， 2023，37（2）： 13-24. （Zhang Shanli， Xie Jialiang， Chen Shuili. Improved NSGA-Ⅲ algorithm based on fuzzy system［J］. Fuzzy Systems and Mathematics， 2023，37（2）：13-24.）