趋优变异反向学习的樽海鞘群与蝴蝶混合优化算法

黄鑫宇 马宁 付伟 季伟东 亓文凤

摘 要：针对蝴蝶优化算法（butterfly optimization algorithm，BOA）易陷入局部最优，且收敛速度慢和寻优精度低等问题，提出了一种趋优变异反向学习的樽海鞘群与蝴蝶混合优化算法（hybrid optimization algorithm for salp swarm and butterfly with reverse mutation towards optimization learning，OMSSBOA）。引入柯西变异对最优蝴蝶个体进行扰动，避免算法陷入局部最优；将改进的樽海鞘群优化算法（salp swarm algorithm，SSA）嵌入到BOA，平衡算法全局勘探和局部开采的比重，进而提高算法收敛速度；利用趋优变异反向学习策略扩大算法搜索范围并提升解的质量，进而提高算法的寻优精度。将改进算法在10种基准测试函数上进行仿真实验，结果表明，改进算法具有较好的寻优性能和鲁棒性。

关键词：蝴蝶优化算法；樽海鞘群优化算法；柯西变异；趋优变异反向学习；领导者策略

中图分类号：TP301   文献标志码：A

文章编号：1001-3695（2024）03-012-0721-08

doi：10.19734/j.issn.1001-3695.2023.07.0328

Hybrid optimization algorithm for salp swarm and butterfly with

reverse mutation towards optimization learning

Huang Xinyu，Ma Ning，Fu Wei，Ji Weidong，Qi Wenfeng

（School of Computer Science & Information Engineering，Harbin Normal University，Harbin 150025，China）

Abstract：To address the problems of the butterfly optimization algorithm，such as include vulnerability to local optima，low optimization accuracy and slow convergence speed，this paper proposed a hybrid optimization algorithm for salp swarm and butterfly with reverse mutation towards optimization learning.The algorithm introduced Cauchy mutation to disturb the optimal butterfly individual to avoid the algorithm falling into local optimization.Embedding the improved salp swarm algorithm（SSA） into BOA，it adjusted the proportion of global exploration and local mining，thereby enhancing the algorithms convergence speed.Using the reverse mutation towards optimization learning strategy，it enhanced the algorithms search space and improved the quality of solutions，consequently bolstering its overall optimization accuracy.The experimental results obtained from conducting simulations on 10 benchmark functions，show the exceptional optimization performance and robustness of the improved algorithm.

Key words：butterfly optimization algorithm；salp swarm algorithm；Cauchy mutation；reverse mutation towards optimization learning；leadership strategy

0 引言

通常情況下，优化算法可以分为基于梯度和基于非梯度两类。基于梯度的算法利用连续或部分连续的目标函数以及它的梯度信息来调整搜索方向和步长，以实现优化过程的调整。由于找到一个可解决各种复杂问题的目标函数极其困难，所以无须任何连续目标函数的非梯度方法开始作为可替代的搜索技术被广泛使用，其中最重要的方法之一是元启发式算法。在过去的十年里，受自然现象、社会行为或物理规则所启发的元启发式技术已广泛流行。

蝴蝶优化算法（BOA）是Arora等人［1］于2019年提出的一种模拟蝴蝶觅食和交配行为的新群智能优化算法，在理想状态下，BOA中每只蝴蝶均具备可相互吸引彼此香味以及朝着香味最浓的蝴蝶移动从而散发更多香味的两个特点。研究表明，BOA在求解非约束常规数学函数方面具有显著的性能，但也存在群智能优化算法的共性问题，如全局勘探能力差且易陷入局部最优。针对这些问题，很多学者对此不断进行改进。Long等人［2］引入基于logistic模型的动态惯性权重作为第一策略，对位置更新方程进行了修正。Bendahmane等人［3］引入了一种基于交叉算子的新变体xBOA，在全局位置更新时进行突变，提高算法跳出局部最优的能力。Xia等人［4］引入正弦余弦算子在局部位置更新时进行突变，从而提高了算法的局部开采能力。Mortazavi等人［5］开发一种新的模糊决策策略，并引入一种新的辅助概念“虚拟蝴蝶”，以提高标准BOA的寻优性能。Fan等人［6］在BOA基础上引入新的香味系数，并在全局勘探和局部开采阶段引入新的迭代和更新策略，以此来提高算法的搜索精度和减少算法的迭代次数。Li等人引入反向学习策略以提高BOA种群多样性。Xu等人将BOA同黑寡妇算法进行混合，从而避免算法陷入局部最优。徐杰等人通过拉丁超立方抽样种群初始化策略提高BOA的全局勘探能力。刘慧等人通过将BOA和粒子滤波算法结合，解决粒子多样性减少等问题。上述算法均使得BOA的整体性能有所提升，但算法仍需花费大量时间去搜索全局最优解，对于BOA易早熟收敛、勘探和开采比例不平衡等问题还需要进行更多深入研究。

1 蝴蝶优化算法及其局限性

1.1 蝴蝶优化算法

蝴蝶优化算法受蝴蝶觅食和交配行为的启法，在蝴蝶飞行的过程中，蝴蝶会根据适应度函数产生一定强度的香味，且蝴蝶之间能够感知和区分不同的香味浓度。假设蝴蝶产生的香味浓度与它们的适应度值成正比，蝴蝶个体的适应度值会随着位置更新而发生相应变化。当一只蝴蝶探测到比自身香味更浓烈的蝴蝶个体时，它就会向其所在方向移动，该阶段被称为全局勘探。相反，如果蝴蝶探测不到该区域有比自身香味更浓烈的蝴蝶个体时，就会在该区域随机移动，该阶段被称为局部开采。香味浓度的计算公式为

fi=cIa（1）

其中：f为香味的感知强度；c为感官模态；I为刺激浓度，受蝴蝶个体适应度值影响；a为依赖于模态的幂指数。在BOA中，通常设置a=0.1，c=0.01。在极端的情况下，a=1表示第i只蝴蝶散发的香味信息可以全部被种群内的其他蝴蝶个体感知，a=0表示第i只蝴蝶散发的香味信息不能被其他蝴蝶感知。

蝴蝶的搜索模式分为两个阶段：

a）全局勘探阶段。蝴蝶个体在飞行过程中散发香味，且每只蝴蝶会根据嗅到的香味浓度朝浓度最强的蝴蝶个体趋近。该阶段位置更新公式定义为

2 趋优变异反向学习樽海鞘群与蝴蝶混合优化算法

2.1 柯西变异

传统的BOA是通过自身香味在搜索范围里彼此交互信息来寻找食物源，这些香味与其适应度具有相关性。由1.2节可知，在BOA全局勘探过程中，如若最好的蝴蝶被困在任何局部最小值中，将会有近80%的蝴蝶被其吸引，从而陷入局部最优，导致算法过早收敛。为解决蝴蝶个体的盲目跟随性问题，在BOA全局勘探阶段引入柯西变异。柯西变异主要利用柯西分布函数生成的随机数来实现其变异操作。Cauchy分布函数为

图2为柯西分布函数的概率密度图像，图中柯西分布为厚尾分布，其概率密度函数呈长尾状态，这种厚尾性表明柯西变异策略具有较高概率跳出局部最优解，并为其继续探索全局最优解提供了可能性。柯西分布函数在峰值处有较高的概率密度，但随着距离峰值越远，概率密度下降的速度相对较慢，趋向于零的速度也较慢。这种特性使得柯西分布能够生成与原点相距較远的随机数，具有较强的扰动能力，变异后的个体也具备快速跳出局部极值的能力。利用柯西分布函数特征对最优蝴蝶个体（g*）进行柯西变异，增加其跳出局部极值的能力，避免其成为局部最优解而吸引其他蝴蝶个体陷入局部区域。当其跳出当前位置成功转移到其他位置后，被其吸引的其他蝴蝶个体可以在新区域内搜索是否存在更优的解，一定程度上缓解了蝴蝶个体的盲目性，提高了BOA的收敛精度。本文根据式（6）对最优蝴蝶个体（g*）进行变异处理。受文献的启发，将惯性权重因子ω同柯西变异相结合，用来调节变异的扰动程度，Tmax为最大迭代次数。

2.2 改进的樽海鞘群算法

通过柯西变异策略对最优蝴蝶个体（g*）进行扰动，大大减少了由BOA中最优蝴蝶个体（g*）被困在局部最小值导致的其他蝴蝶个体被其吸引陷入局部最优的情况。柯西变异策略的引入虽提高了BOA跳出局部最优的能力，但整体性能提高幅度不大。因此要想从根本上提高算法性能，还要着重于平衡全局勘探和局部开采在搜索过程中所占的比重。在群智能优化算法中，算法在迭代初期通过进行全局勘探广泛搜索整个解空间，从而确定全局最优解的大致范围，局部开采需要在算法确定全局最优解大致位置后，对其所在的局部区域进行精准搜索和调整，从而快速找到全局最优解。在BOA中，由于切换概率P预定的常数值不变，算法在搜索过程中很容易出现搜索错误现象，即算法在通过全局勘探已经确定全局最优解的大致范围后的情况下，仍然选择进行全局勘探，而非局部开采。在算法搜索过程中，局部开采所占比重过少会导致算法找到全局最优解的时间过长甚至找不到全局最优解。为解决由于切换概率P恒定而引起BOA进行全局勘探和局部开采比重不平衡的问题，本文将改进后的樽海鞘群领导者策略嵌入BOA的局部开采阶段，利用领导者策略具备的动态调整性来平衡BOA进行全局勘探和局部开采的比重，减少算法的寻优时间，提高算法的收敛速度。

樽海鞘群算法（salp swarm algorithm，SSA）是Mirjalili等人［12］于2017年提出的一种用于解决多目标优化问题的新型算法。该算法的主要思想来源于樽海鞘的群聚行为，且算法的适应度值取决于食物资源的质量。在全局勘探阶段，SSA选取适应度最高的个体作为领导者，而领导者通常会选择一条最短路径，带领其他樽海鞘前往食物源，这一过程就是算法寻找全局最优解的过程。在局部开采阶段，领导者可以引导群体成员集中在具有潜力的区域进行更深入的搜索和利用，以加快优化过程的收敛速度。这种局部开采方式有助于集中资源和精力来发现更优的局部解，并在全局和局部之间实现平衡。SSA与BOA通过恒定概率P改变搜索状态不同，其领导者策略具备动态调整性，能根据当前环境条件和群体状态适时地调整全局勘探和局部开采的比例。在搜索初始阶段，领导者会更加侧重于全局勘探，以探索更广阔的解空间。在搜索后期，随着迭代次数的增加，领导者逐渐增加局部开采的比例，以便更加精准地寻找最优解。

近几年，SSA开始用于同其他群智能优化算法进行混合，混合后算法兼备二者优点，可以更好地提高算法寻优性能。如Fan等人将SSA的收敛因子引入鲸鱼优化算法的包围猎物阶段，从而提高算法的开采能力。试想将SSA和BOA两种算法进行混合，利用SSA中领导者策略的动态调整性改善BOA中切换概率P恒定导致的算法搜索比重不平衡的问题，从而达到提高算法的寻优性能和收敛速度的目的。因此，本文将领导者策略嵌入到BOA局部开采阶段后，有效增加了BOA进行局部开采的比重，弥补了由BOA自身局限性导致算法在搜索过程中全局勘探所占比重大而局部开采所占比重小的问题，提高了算法整体的收敛速度。领导者策略具体位置更新公式为：在BOA局部开采（r3>p）的前提下，当c3≤0.5时领导者执行式（7）；当c3>0.5时领导者执行式（8）。

选取表1中典型多峰测试函数进行消融测试，以证明改进的樽海鞘群领导者策略具备有效性。测试中种群数量为30，迭代次数为500。图3（a）为在BOA中仅加入领导者策略（SSBOA）和BOA的收敛曲线对比。如图3（a）所示，与BOA相比，SSBOA具备更好的收敛精度和更少的迭代次数，这表明领导者策略所具备动态调整性在嵌入BOA中后可以有效平衡全局勘探和局部开采的比重，减少算法搜索到全局最优解的时间。图3（b）为在BOA中仅加入改进的樽海鞘群领导者策略（BSSBOA）同BOA的收敛曲线对比。如图3（b）所示，同SSBOA相比，BSSBOA搜索到全局最优解所用的迭代次数更少，这表明引入寻优者策略后，领导者在最优解附近优先搜索可以加快算法的收敛速度。

综上所述，将改进的樽海鞘群领导者策略同BOA进行混合，改善了算法全局勘探与局部开采效率不平衡的问题，进而提升了算法的整体性能。

2.3 趋优变异反向学习

标准BOA中，蝴蝶的位置更新方式是通过在每次迭代时计算蝴蝶个体适应度值并与上一次迭代时的适应度值进行比较，选择适应度值最好的蝴蝶个体进入下一次迭代，但蝴蝶个体位置更新较随机且位置变化幅度不大，这便会导致算法后期收敛速度较慢。众所周知，群智能优化算法的迭代过程是通过搜索区域的变换来寻找最优解的过程，其中反向学习（opposition-based learning，OBL）［14］是实现区域变换搜索的一种模式。反向学习的中心思想是求出问题中可行解的反向解，并对可行解和反向解同时进行评估，筛选出其中适应度值最优的解进行下一次迭代，以保证种群质量。如若对蝴蝶个体位置进行变异干扰的同时扩大BOA的搜索范围，便可达到提高解的质量和算法收敛速度的目的。因此本文根据遗传算法［15］中的变异概率思想和文献的启发，在BOA全局勘探阶段引入趋优变异反向学习策略对BOA中的蝴蝶个体进行干扰，从而确保适应度值最优的蝴蝶个体顺利进入下一次迭代。为了更清晰地解释反向学习的概念，对反向解和反向学习进行如下定义：

定义1 反向解。假设在［a，b］上存在一个实数x，则实数x的反向解可以表示为=a+b-x。

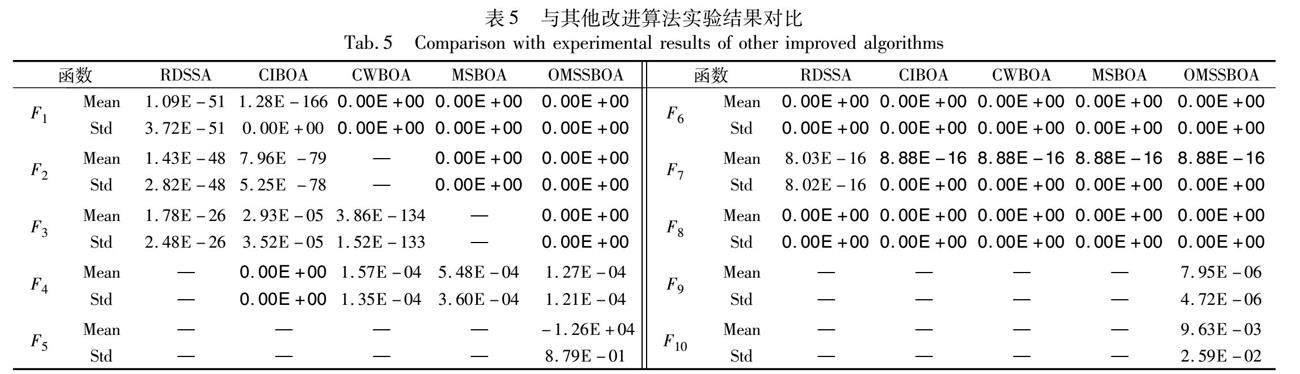
定义2 反向学习。在反向解定义的基础上，可以得出反向学习定义如下：假设P=（x1，x2，…，xi，…，xn）为一个N维向量空间的点，且xi∈［ai，bi］，i∈［1，2，…，n］，根据反向解的定义可知，P的反向解为=（1，2，…，i，…，n），其中i=k（ai+bi）-xi，k为［0，1］随机分布的一般化系数。设适应度函数为f，如果f（）

反向学习策略的引入扩大了BOA搜索范围，但反向学习策略并不能做到对蝴蝶个体位置进行精准干预。首先群智能优化算法中的收敛速度是指算法在运行过程中逐渐接近最优解的速度，可近似通过蝴蝶个体向最优解趋近过程中的这段距离来估算，在BOA位置更新方式中，蝴蝶个体是随机生成的，这意味着在最优解附近出生的蝴蝶个体的收敛速度一定有了大幅度的提升，但相比较其他随机生成的蝴蝶个体来说，其距离不好估计，收敛速度也就无法预知；其次，在算法初期，反向学习通过生成反向解逐渐改进当前解，在一定程度上提升了解的质量，在算法后期，由于反向解的生成位置相对固定且与可行解之间位置距离较远，BOA因种群多样性较少，在迭代后期蝴蝶位置更新较随机且蝴蝶位置更新幅度并不大，只依靠反向学习不能对蝴蝶个体位置更新进行精准干预。基于上述原因，本文将遗传算法中变异概率融合在反向学习中，遗传算法中变异的本质是随机对个体基因产生变异，从而提升解的质量。将变异概率思想同反向学习结合后，变异反向学习可以产生随机性更强的反向解，对蝴蝶个体位置进行更精准的干预，从而提升解的质量，避免算法早熟收敛。为保证引入变异概率之后算法整体稳定性不被影响，变异概率不宜设置过大，经实验测试得Pr设置为0.08时效果最好。具体表达公式如下：

当b≤Pr时，通过变异反向学习进行蝴蝶位置更新：

xtnew_i=lbi+R（ubi-xti） b≤Pr（11）

当b>Pr时，通过一般反向学习进行蝴蝶位置更新：

xtnew_i=lbi+（ubi-xti） b>Pr（12）

其中：Pr為变异概率，其取值为（0.01，0.10）；R和b为分布于（0，1）的随机数；xtnew_i表示蝴蝶个体经变异反向学习之后得到的新的位置。

变异反向学习的引入一定程度上提升了算法的整体性能，对传统BOA中蝴蝶个体位置更新方式进行有效优化，但是变异反向学习不能保证每次新解的适应度值都一定优于变异前的可行解。因此，本文将通过变异反向学习扰动后的个体和当前种群中最优个体进行凸组合，得到趋优变异反向学习个体，并更新其最新位置，以此保证适应度值最优的个体可以顺利进行下一次迭代。具体公式如式（13）所示，其中a2为［0，1］的随机数。

xt+1i=a2×xtnew_i+（1-a2）×g*（13）

2.4 算法具体描述

OMSSBOA根据所提出的三种改进策略。首先在全局勘探阶段引入柯西变异策略，按照式（6）对最优蝴蝶个体进行扰动，按照式（2）对蝴蝶位置进行更新，增强了算法跳出局部最优的能力；然后继续在全局勘探阶段引入趋优变异反向学习策略，按照式（11）～（13）更新蝴蝶位置，提高解的质量，从而提高算法收敛精度；最后在局部开采阶段引入改进的樽海鞘群领导者策略，按照式（7）（10）平衡BOA全局勘探和局部开采的比重，提高算法的收敛速度和寻优性能。OMSSBOA具体步骤如图4和算法2所示。

算法2 OMSSBOA算法

输入：种群规模N，感官模态c，幂指数a，刺激浓度I，最大迭代次数Tmax，搜索空间维度dim，切换概率P，随机数r3、b、c3，变异概率Pr。

输出：全局最优解。

初始化种群。

while（t≤Tmax）

for i=1：N

根据式（1）计算蝴蝶香味浓度；

end for

找出最优蝴蝶个体位置；

for i=1：N

r3=rand（0，1）；b=rand（0，1）；c3=rand（0，1）；P=0.8；

Pr=0.08

if r3

根据式（6）对最优个体进行扰动；

根据式（2）对位置进行更新；

if b>Pr then根据式（12）进行位置更新；

else根据式（11）进行位置更新；

end if

根据式（13）进行位置更新；

else

if c3>0.5 then根据式（10）进行位置更新；

else根据式（7）进行位置更新；

end if

end if

end for

计算适应度值，并更新最优位置；

end while

输出全局最优解

2.5 时间复杂度

在原始BOA中，设种群规模为N，维度为d，最大迭代次数为Tmax，则原始BOA的时间复杂度为O（N×d×Tmax）。OMSSBOA是以BOA为基础的改进算法，故OMSSBOA的时间复杂度由算法步骤可知，引入柯西变异的时间复杂度为O（N×d×Tmax），引入改进的樽海鞘群领导者策略的时间复杂度为O（N×d×Tmax），引入趋优变异反向学习的时间复杂度为O（N×d×Tmax），因此OMSSBOA时间复杂度为O（N×d×Tmax），与原始BOA相同，可以判定OMSSBOA并未增加算法的计算负担。

2.6 收敛性分析

假设蝴蝶个体的种群总数为N，解空间为S，全局最优解为fgbest，迭代次数为t。群体智能优化算法依靠概率1收敛于全局最优解［18］的充分条件为：

条件1 设F为待求解函数，f为生成解函数，z为S中的一个点，其目的是保证F有一个下确界，τ为随机生成向量。

如果F（f（z，τ））≤F（z），并且

τ∈S，则有F（f（z，τ））≤F（τ）。

定理1 OMSSBOA算法满足条件1。

证明 在OMSSBOA算法中，函数f可以定义为

f（xgbest，gbest）=f（gbest）if f（xgbest）>f（gbest）

f（xgbest）if f（xgbest）

OMSSBOA在每一次迭代过程中都会选择适应度值最优的解，所以算法满足条件1。

条件2 S的任意可测集A，若D∈S且A的测度υ（A）>0，则∏∞j=0（1-μj（A））=0，其中υ（A）>0是A的n维闭包；μj（A）是由测度μj产生A的概率测度。

定理2 OMSSBOA算法满足条件2。

证明 OMSSBOA的寻优过程中都是在有限空间进行的，并且柯西变异扰动、樽海鞘群领导者策略以及趋优变异反向学习的引入均属于独立随机过程，在整个迭代进化过程中，改进算法均采取保留精英个体的策略，故改进算法具备收敛性且符合齐次马尔可夫链。根据OMSSBOA位置更新方式可得，OMSSBOA通过趋优变异反向学习对当前解进行变异，确保适应度值最优个体进入下次迭代，故随着迭代一定具备Si（t+1）=S，t→∞，即存在D∈S有：

∏∞j=0（1-μj（A））=0，μj（A）=∑Nj=1μj（A）=1，limj→∞（1-∑Nj=1μj（A））j=0

所以OMSSBOA符合齊次马尔可夫链且满足条件2。

综上所述，OMSSBOA满足定理1和2，故其可以依靠概率1收敛到全局最优解。

3 仿真实验及分析

3.1 参数设置

实验采用Windows 10操作系统，并使用具有64位Intel CoreTM i5-8300H CPU @ 2.30 GHz的计算机配置。仿真软件采用MATLAB 2018b版本。为了确保实验的客观性，本文设定了以下实验参数：初始种群规模为30，最大迭代次数为500，感官模态c设置为0.01，幂指数a设置为0.1，切换概率参数P设置为0.8，变异概率参数Pr设置为0.08。

3.2 基准测试函数

本文选择了10个基准测试函数来验证OMSSBOA的改进效果。F1～F4为单峰基准测试函数，单峰基准测试函数具有一个唯一的全局最优解，没有其他的局部最优解，一般用于检验算法的收敛精度和收敛速度。F5～F10为多峰基准测试函数，多峰基准测试函数的特点是具有多个峰值，所以其具备多个局部最优解，一般用于检验算法跳出局部最优的能力。实验中如若数据达到基准测试函数的理论极值，则证明算法效果最好。基准测试函数如表2所示。

3.3 实验结果与分析

3.3.1 与原始算法对比

通常情况下，对比实验选择用平均值来衡量算法的寻优性能，用标准差来衡量算法的稳定性和鲁棒性，故将OMSSBOA同原始算法BOA和SSA分别在d=30、d=100及d=500条件下独立运行30次，并将运行后所获得的平均值和标准差之间的数据进行对比分析，从而验证OMSSBOA算法的整体性能。本文所有表格中均已用黑体标注对比实验结果的最优解。

如表3数据所示，从寻优性能的角度分析，在单峰基准测试函数中，OMSSBOA的平均值和标准差在F1～F3中均达到了理论值0，除函数F4上OMSSBOA收敛精度略高于其他算法之外，OMSSBOA的收敛精度和稳定性明显高于BOA和SSA。在多峰基准测试函数中，OMSSBOA在测试函数F6和F8上取得了理论值0，对于函数F7来说，OMSSBOA的收敛精度平均值为8.882E-16，相比于BOA高出7个精度，比SSA高出16个精度，且标准差稳定在0。在函数F9和F10上，OMSSBOA也表现出了很好的寻优性能。虽然在函数F5上收敛精度略高于原始算法，但OMSSBOA的稳定性和鲁棒性更好，由此可以证明改进的混合算法克服了BOA因搜索模式导致在多峰基准函数中寻优精度不高的局限性。从维度的角度分析，已知求解函数的复杂度同基准测试函数的维度成正比，即复杂度越高，算法的寻优过程越复杂，这便可能导致算法的收敛速度变慢。从实验数据可以得出，随着维度增高，收敛精度和稳定性效果最好的是OMSSBOA，其次是BOA，最后是SSA。OMSSBOA在不同维度下实验数据变化不大，说明OMSSBOA在高维度条件下同样具备很好的寻优性能。

综上所述，OMSSBOA改善了蝴蝶最优个体易陷入局部最优值，平衡了算法的全局勘探和局部开采比重，提高了算法全局勘探的效率，一定程度上提高了BOA的寻优性能，且有效改善了BOA的三个局限性。

3.3.2 与不同群智能算法对比

在搜索空间维度为d=30与d=500条件下，将OMSSBOA同灰狼优化算法（GWO）、鲸鱼优化算法（WOA）和飞蛾扑火优化算法（MFO）在基准测试函数F1～F10上进行寻优对比。如表4实验数据所示，从寻优性能的角度分析，在单峰测试函数中，OMSSBOA平均收敛精度最高且稳定性最好，其次是WOA。虽然OMSSBOA在函数F4上未取到理论极值0，但同MFO相比，OMSSBOA在d=500时高出其8个精度。虽然WOA和OMSSBOA在多峰测试函数F6、F8上均取得理论值0，但是OMSSBOA在多峰测试函数上的整体稳定性要好且收敛精度略高于WOA。从维度的角度分析，OMSSBOA在d=30和d=500之间平均值和标准差变化最小，其次是WOA。因此OMSSBOA在低维和高维的条件下，其收敛效果均优于其他群智能算法。

3.3.3 与其他改进算法实验结果对比

将OMSSBOA同RDSSA、CIBOA、CWBOA与MSBOA四种优秀的改进算法进行对比，在对比实验中严格按照控制单一变量的原则，使每个算法均在搜索空间维度为d=30的条件下独立运行30次。

如表5实验数据所示（表中“—”代表无数据），从寻优性能的角度分析，在单峰基准测试函数中，CWBOA和MSBOA在F1、F2上取得理论值0，OMSSBOA在F1～F3上取得理论极值0。在F1～F3上OMSSBOA收敛精度和稳定性最好。CIBOA在函数F4上性能最好且取得了理论极值0。在多峰基准测试函数中，除RDSSA性能略低以外，其他改进算法均在F6～F8上获得了不错的收敛精度，且OMSSBOA在函数F5、F9、F10的整体性能略优于其他算法。故OMSSBOA同其他改进算法相比，初步具备竞争性、可行性及有效性。

3.3.4 算法收敛速度分析

在d=30的条件下，将OMSSBOA、BOA、SSA、GWO、WOA、CWBOA、RDSSA独立运行30次，得到的平均收敛速度曲线如图5所示。

本文选取了函数F1、F2、F3、F4、F6、F7、F8、F9、F10的函数图像。如图5所示，对于单峰基准测试函数，在函数F1～F3中，OMSSBOA搜索到全局最优解所需迭代次数最少。在函数F4中，OMSSBOA虽然下降速度很快，但RDSSA的收敛精度要优于OMSSBOA。对于多峰基准测试函数，BOA和SSA在多峰测试函数的条件下更易看出同其他算法相比，其下降速度更慢、更易陷入局部最优。在函数F8中，WOA、CWBOA、RDSSA均取到理论极值0，但是RDSSA和OMSSBOA在算法初期下降速度更快，且OMSSBOA具备更快的收敛速度，在50代以内搜索到最优值。在函数F9和F10中，OMSSBOA虽未取得理论值，但相比其他算法具备更高的收敛精度。综上所述，OMSSBOA改善了原始BOA和SSA在多峰测试函数中收敛精度不高、迭代时间长且易陷入局部最优等问题，除函数F4中，OMSSBOA的性能略低于RDSSA以外，OMSSBOA在其他所给函数中均优于其他算法，因此OMSSBOA初步具備可行性和竞争性。

3.3.5 消融实验

将仅加入柯西变异策略（CBOA）、改进的樽海鞘群领导者策略（BSSBOA）、仅加入趋优变异反向学习策略（OLBOA）同OMSSBOA在维度为d=30的条件下独立运行30次进行消融实验，进一步判断算法的寻优性能和稳定性。

由表6数据可知，从单峰测试函数方面分析，除OLBOA和OMSSBOA在函数F1～F3取得理论值外，CBOA和BSSBOA虽未达到理论值，但其平均值和标准差同BOA相比均有一定程度的增加，CBOA在F1上的平均值提高了47个精度，这表明引入柯西变异策略对最优蝴蝶个体进行扰动可以避免其陷入局部最优值，从而提高算法收敛精度。BSSBOA在F2上的平均值提高了118个精度，这表明引入改进的樽海鞘群领导者策略后，有效地平衡了BOA的全局勘探和局部开采的比例，提高了局部开采的效率。由OLBOA在表6中单峰函数的平均值均为效果最好数据可知，在全局勘探阶段引入趋优变异反向学习，提高了算法的收敛精度，保证每一次种群迭代时均是最优适应度值个体参与下次循环，很大程度上提高了算法的寻优性能。变异概率与反向学习的结合也没有破坏算法的稳定性和鲁棒性，这一点可通过OLBOA的标准差在大部分测试函数上均可取得理论值来推断。从多峰测试函数方面分析，寻优性能依次是OMSSBOA>CBOA>BSSBOA>OLBOA，这表明柯西变异策略改善了BOA因其局限性造成的在多峰测试函数中过早收敛的问题，同其他两种策略有效结合，最大化地提高了算法的收敛精度。

综上所述，融合三种策略的OMSSBOA的整体寻优性能很大程度上优于BOA。

4 结束语

针对BOA算法的三个局限性，提出了一种趋优变异反向学习的樽海鞘群与蝴蝶混合优化算法。首先，在全局勘探阶段引入柯西变异策略对最优蝴蝶个体进行扰动，增强算法跳出局部最优的能力；其次，在局部开采阶段引入改进的樽海鞘群领导者策略平衡BOA全局勘探和局部开采的比重，对算法收敛速度慢的问题进行改善；最后，在全局勘探阶段引入趋优变异反向学习策略，扩大算法搜索范围，解决蝴蝶个体位置更新较随机且变化幅度不大的问题，保证每次迭代时蝴蝶个体的质量。经10种基准测试函数仿真实验表明，OMSSBOA能解决BOA因自身局限性导致的在进行高维和多峰函数求解时寻优性能不高的问题，具有可行性和竞争性。下一步的研究内容是将OMSSBOA算法应用于具体的工程实际问题中，提高OMSSBOA解决实际问题的能力。

參考文献：

［1］Arora S，Singh S.Butterfly optimization algorithm：a novel approach for global optimization［J］.Soft Computing，2019，23：715-734.

［2］Long Wen，Jiao Jianjun，Wu Tiebin，et al.A balanced butterfly optimization algorithm for numerical optimization and feature selection［J］.Soft Computing，2022，26（21）：11505-11523.

［3］Bendahmane A，Tlemsani R.Unknown area exploration for robots with energy constraints using a modified butterfly optimization algorithm［J］.Soft Computing，2023，27（7）：3785-3804.

［4］Xia Qingyu，Ding Yuanming，Zhang Ran，et al.Blind source separation based on double-mutant butterfly optimization algorithm［J］.Sensors，2022，22（11）：3979.

［5］Mortazavi A，Moloodpoor M.Enhanced butterfly optimization algorithm with a new fuzzy regulator strategy and virtual butterfly concept［J］.Knowledge-Based Systems，2021，228：107291.

［6］Fan Yuqi，Shao Junpeng，Sun Guitao，et al.A self-adaption butterfly optimization algorithm for numerical optimization problems［J］.IEEE Access，2020，8：88026-88041.

［7］Li Yu，Yu Xiaomei，Liu Jingsen.An opposition-based butterfly optimization algorithm with adaptive elite mutation in solving complex high-dimensional optimization problems［J］.Mathematics and Compu-ters in Simulation，2023，204：498-528.

［8］Xu Hui，Lu Yanping，Guo Qingqing.Application of improved butterfly optimization algorithm combined with black widow optimization in feature selection of network intrusion detection［J］.Electronics，2022，11（21）：3531.

［9］徐杰，鲁海燕，赵金金，等.拉丁超立方抽样的自适应高斯小孔成像蝴蝶优化算法［J］.计算机应用研究，2022，39（9）：2701-2708，2751.（Xu Jie，Lu Haiyan，Zhao Jinjin，et al.Self-adaptive Gaussian keyhole imaging butterfly optimization algorithm based on Latin hypercube sampling［J］.Application Research of Computers，2022，39（9）：2701-2708，2751.）

［10］刘慧，姜雨汐.融合分数阶和蝴蝶优化的改进粒子滤波算法［J］.小型微型计算机系统，2022，43（4）：828-833.（Liu Hui，Jiang Yuxi.Improved particle filter algorithm incorporating fractional-order and butterfly optimization［J］.Journal of Chinese Computer Systems，2022，43（4）：828-833.）

［11］高文欣，刘升，肖子雅，等.柯西变异和自适应权重优化的蝴蝶算法［J］.计算机工程与应用，2020，56（15）：43-50.（Gao Wenixin，Liu Sheng，Xiao Ziya，et al.Butterfly optimization algorithm based on Cauchy variation and adaptive weight［J］.Computer Engineering and Applications，2020，56（15）：43-50.）

［12］Mirjalili S，Gandomi A H，Mirjalili S Z，et al.Salp swarm algorithm：a bio-inspired optimizer for engineering design problems［J］.Advances in Engineering Software，2017，114：163-191.

［13］Fan Qian，Chen Zhenjian，Zhang Wei，et al.ESSAWOA： enhanced whale optimization algorithm integrated with salp swarm algorithm for global optimization［J］.Engineering with Computers，2022，38（S1）：797-814.

［14］Tizhoosh H R.Opposition-based learning：a new scheme for machine intelligence［C］//Proc of International Conference on Computational Intelligence for Modelling，Control and Automation，International Conference on Intelligent Agents，Web Technologies and Internet Commerce.Piscataway，NJ：IEEE Press，2005：695-701.

［15］Holland J H.Adaptation in natural and artificial systems：an introductory analysis with applications to biology，control，and artificial intel-ligence［M］.Cambridge，MA：MIT Press，1992.

［16］左汶鹭，高岳林.基于随机邻域变异和趋优反向学习的差分进化算法［J］.计算机应用研究，2023，40（7）：2003-2012.（Zuo Wenlu，Gao Yuelin.Differential evolutionary-based on random neighborhood mutation and optimal opposition-based learning［J］.Application Research of Computers，2023，40（7）：2003-2012.）

［17］李守玉，何慶，杜逆索.分段权重和变异反向学习的蝴蝶优化算法［J］.计算机工程与应用，2021，57（22）：92-101.（Li Shouyu，He Qing，Du Nisuo.Butterfly optimization algorithm piecewise weight and mutation opposition-based learning butterfly optimization algorithm［J］.Computer Engineering and Applications，2021，57（22）：92-101.）

［18］Solis F J，Wets R J B.Minimization by random search techniques［J］.Mathematics of Operations Research，1981，6（1）：19-30.

［19］Mirjalili S，Mirjalili S M，Lewis A.Grey wolf optimizer［J］.Advances in Engineering Software，2014，69（3）：46-61.

［20］Mirjalili S，Lewis A.The whale optimization algorithm［J］.Advances in Engineering Software，2016，95（5）：51-67.

［21］Mirjalili S.Moth-flame optimization algorithm： a novel nature-inspired heuristic paradigm［J］.Knowledge-Based Systems，2015，89（11）：228-249.

［22］陈雷，蔺悦，康志龙.基于衰减因子和动态学习的改进樽海鞘群算法［J］.控制理论与应用，2020，37（8）：1766-1780.（Chen Lei，Lin Yue，Kang Zhilong.Improved salp swarm algorithm based on reduction factor and dynamic learning［J］.Control Theory & Applications，2020，37（8）：1766-1780.）

［23］王依柔，张达敏，徐航，等.基于自适应扰动的疯狂蝴蝶算法［J］.计算机应用研究，2020，37（11）：3276-3280.（Wang Yirou，Zhang Damin，Xu Hang，et al.Crazy butterfly algorithm based on adaptive perturbation［J］.Application Research of Computers，2020，37（11）：3276-3280.）

［24］陈俊，何庆.基于余弦相似度的改进蝴蝶优化算法［J］.计算机应用，2021，41（9）：2668-2677.（Chen Jun，He Qing.Improved butterfly optimization algorithm based on cosine similarity［J］.Journal of Computer Applications，2021，41（9）：2668-2677.）