“三数一差”与图表同行

张卫

平均数、中位数和众数是反映一组数据集中趋势的统计量，简称“三数”，方差反映了一组数据的波动大小，四者加起来简称“三数一差”，它们是数据分析的核心内容和重要指标，考查“三数一差”时，很多问题是通过图表给出数据信息.

要求通过计算“三数一差”分析数据特征．

一 从统计表中提取数据

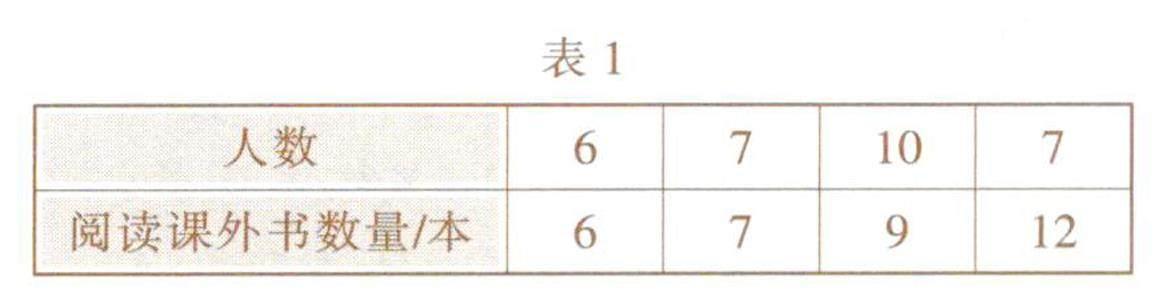
例1 （2023·枣庄）4月23日是世界读书日，学校举行“快乐阅读，健康成长”读书活动，小明随机调查了本校七年级30名同学近4个月内每人阅读课外书的数量，数据如表1所示．

閱读课外书数量的中位数和众数分别是（ ）．

A.8和9 B.10和9

C.7和12 D.9和9

解析：根据统计表所提供的信息，将统计表中的30个数据按照大小进行排列，可以发现处于最中间的第15个和第16个数据都是9，所以中位数为9+9／2＝9．这30个数据中，9出现10次，出现次数最多，所以众数为9．故选D．

二 从扇形图中分析数据

例2 八（1）班举行投篮球比赛，每人投6次球，投进1球得1分．图1是班上所有学生得分的扇形图，下列关于班上所有学生得分的统计量的说法中，正确的是（ ）．

A.众数为2 B.众数为6

C.平均数为1.8 D.中位数为4

解析：众数是出现次数最多的数据，对于扇形图而言则是面积最大的扇形所对应的数据，可以看出，得2分的所占面积比例最大，所以众数为2，A选项正确．由图可知，将得分按从小到大的顺序排列后，处于中间位置的数据应在3分区域内，因此中位数为3．根据各数据所占比例可求得平均数为0×100-10+2×35%+3×15%+4×20％+5×15%+6×5%=3．故选A．

三 从条形图中整理数据

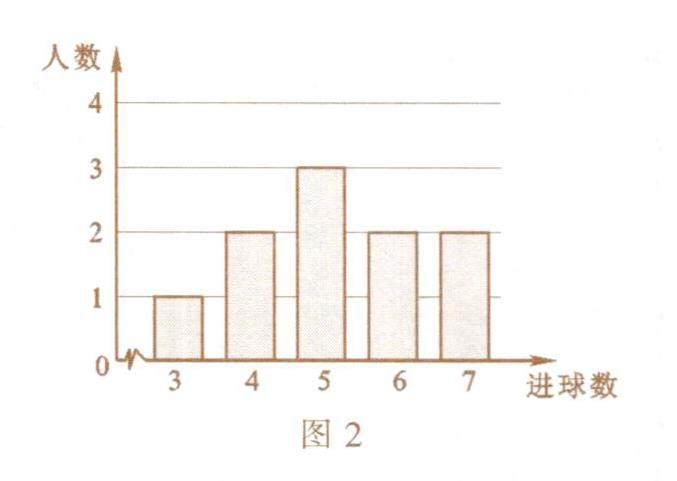
例3 为检测学校足球队的训练效果，从队中随机抽取10名队员进行射门检测，进球数统计如图2所示．对于这10名队员的射门进球数，下列说法中错误的是（ ）．

A.中位数是5 B.众数是5

C.平均数是5.2 D.方差是2

解析：从条形图中分析数据时，众数是最高的小长方形对应的数据，因此众数是5．把这10名队员射门进球数从小到大排列，排在第5和第6的数都是5，所以中位数是5．这10个数据的平均数是1／10×（3+4×2+5×3+6×2+7×2）=5.2，方差是1／10×[（3-5.2）2+2×（4-5.2）2+3×（5-5.2）2+2×（6-5.2）2+2×（7-5.2）2]=1.56.故选D．

四 从折线图中观察数据

例4 （2022·菏泽）射击比赛中，某队员的10次射击成绩（单位：环）如图3所示，则下列结论中错误的是（ ）．

A.平均数是9 B.中位数是9

C.众数是9 D.方差是0.8

解析：观察折线图可知，这组数据的平均数为1／10×（8.4+8.6+8.8+9+9+9+9.2+9.2+9.4+9.4）=9，中位数为9+9／2=9，众数为9，方差为1／10×[（8.4-9）2+（8.6-9）2+（8.8-9）2+3×（9-9）2+2x（9.2-9）2+2×（9.4-9）2]=0.096．故选D.

试金石

1.小楠所在社会实践小组的同学们到附近七个社区宣传“垃圾分类”知识，他们记录了各社区参与活动的人数，并制作了如图4所示的折线统计图，由统计图可知，这组数据的众数和中位数分别是（ ）．

A.42，40 B.42，38 C.40，40 D.38，42

2.八年级260名学生参加捐赠图书活动．活动结束后随机调查了部分学生每人捐赠图书的数量，并按照捐赠图书数量分为四种类型．A类：5本；B类：6本；C类：7本；D类：8本，最后，根据统计数据绘制了条形统计图（图5）和扇形统计图（图6）．

（1）本次调查获取的样本数据的中位数为________，在扇形统计图中，m的值为________．

（2）求样本数据的平均数．

（3）根据样本数据估计这260名学生共捐赠图书多少本．

（参考答案在本期找）