数据分析 创新中考

于秀埔

近年来，中考试卷中与数据分析有关的考题比较多，其中不乏具有创新性的题目．下面选取几例进行分析，供同学们学习时参考．

一 不受影响的统计

例1 （2023·衢州）某公司5名员工在一次义务募捐中的捐款额（单位：元）为30，50，50，60，60．若捐款最少的员工又多捐了20元，则分析这5名员工捐款额的数据时，不受影响的统计量是（ ）．

A.平均数 B.中位数 C.众数 D.方差

解析：由题意知，捐款最少的员工又多捐了20元，于是5个数据分别是50，50，50，60，60，则从小到大的顺序不变，即中位数不变，而平均数、众数、方差都要用到第一个数，故不受影响的统计量是中位数．选B．

二 没有出现的数字

例2 （2023·杭州）将一枚质地均匀的正方体骰子（六个面分别标有数字1，2，3，4，5，6）投擲5次，分别记录每次骰子向上的一面出现的数字，根据下面的统计结果，能判断记录的这5个数字中一定没有出现数字6的是（ ）．

A.中位数是3，众数是2

B.平均数是3，中位数是2

C.平均数是3，方差是2

D.平均数是3．众数是2

解析：当中位数是3，众数是2时，记录的5个数字可能为2，2，3，4，6或2，2．3，5，6，故A选项不符合题意.

当平均数是3，中位数是2时，5个数之和为15，记录的5个数字可能为1，1，2，5，6或1，2，2，4，6或2，2，2，3，6，故B选项不符合题意．

当平均数是3，方差是2时，5个数之和为15.假设6出现了1次，方差最小的情况下另外4个数为2，2，2，3，此时方差s2=1/5×[3×（2-3）2+（3-3）2+（6-3）2]=2.4>2．因此假设不成立，即一定没有出现数字6，故C选项符合题意．

当平均数是3，众数是2时，5个数之和为15.2至少出现2次，记录的5个数字可能为1，2，2，4，6或2，2，2，3，6，故D选项不符合题意．

综上，选C．

三 与遮盖无关的统计量

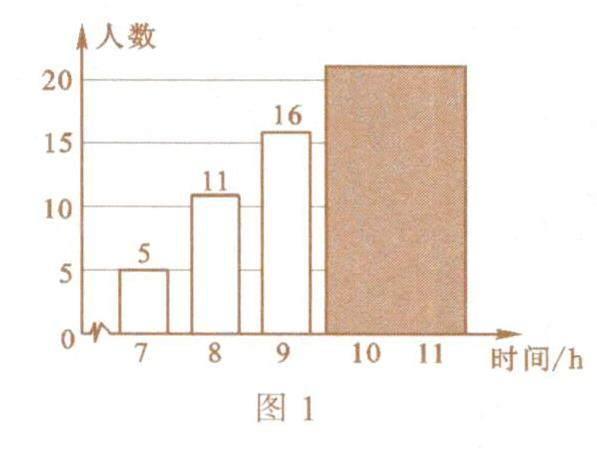
例3 （2022·南充）为了解“睡眠管理”落实情况，某中学随机调查了50名学生每天的平均睡眠时间（时间均保留整数）．将样本数据绘制成统计图（图1），其中有两个数据被遮盖，关于睡眠时间的统计量中，与被遮盖的数据无关的是（ ）．

A.平均数 B.中位数 C.众数 D.方差

解析：由统计图可知，平均数无法计算，众数无法确定，方差无法计算，而中位数是（9+9）÷2=9，与被遮盖的数据无关．选B．