如何通过专项练习促进对“最优方案”的理解

丁玉成

教学了人教版教材四年级下册的“租船问题”后，可以通过以下练习帮助学生巩固解决问题的策略和方法，感受优化思想。

一、设计“解读方案”的练习，提炼最优方案的必要条件

教师出示练习题一：四（1）班50名学生在2位老师的带领下租车前往科技园参观，现有两种车辆可供选择，怎样租车最省钱？

1.解读设计方案。

教师出示4名学生设计的方案。

兰兰设计的方案：60÷6=10（元）， 64÷8=8（元）。

可可设计的方案：（50+2）÷8=6（辆）……4（人），需要6辆大车、1辆小车。

涵涵设计的方案：8+4=12（人），12÷6=2（辆），需要5辆大车、2辆小车。

琪琪设计的方案：5×64+2×60=440（元）。

在教学反馈中，教师让学生说说每个算式的含义。

2.分析必要条件。

教师引导学生思考：兰兰方案中的算式求出了什么？涵涵为什么要对可可的方案进行调整？通过师生讨论、交流，明白怎样租车最省钱。

教师提问：“想要找到最省钱的租车方案，需要具备什么条件？”在此基础上，整体介绍最省钱的租车方案。

二、设计“方案比较”的练习，提升确定最优方案的能力

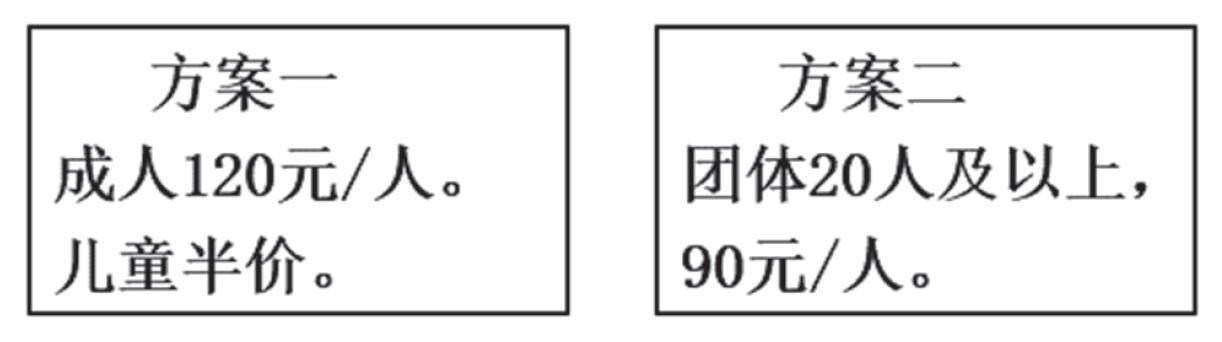
教师出示练习题二：某旅行社推出“迷人森林景区一日游”的两种价格方案。

有三个20人的团队同时一日游。A团队10大10小，B团队15大5小，C团队5大15小。请分别为他们选出最省钱的方案。

1.预测合理的方案。

预测三个团队最省钱的方案分别是哪一个？说明理由。

2.感悟最优方案的条件。

（1）算一算，确定每队的最优购票方案。想一想，为什么每队的最优方案会不同？

（2）成人和儿童的人数对最优方案有什么影响？成人和儿童人数相同时，两种方案的总价一定相同吗？教师要引导学生发现：两种方案的总价是否相同不仅与人数有关，还与团体票价的制订方式有关。

三、设计“方案确定”的练习，寻求不同方案的平衡界点

教师出示练习题三：春节到了，旅行社对“迷人森林景区一日游”的团体票方案进行了调整。

有一行12人去景区游玩，算一算、比一比，采用哪种方案更划算？

1.解讀信息。

与练习题二相比，这道题有什么特点？引导学生发现：成人和儿童人数未知时，不能通过计算来确定最优方案。

2.方案确定。

（1）讨论方法。

教师提问：“总共12人，是不是在6大6小的情况下，两种方案的总价相同？”引导学生发现：买95元/人的团体票价，超过了成人和儿童票价的平均数。

（2）分析平衡界点。

引导学生运用列表法，寻找两种方案总价相同时成人和儿童的人数情况。

（3）提炼最优方案。

让学生描述12人的团体怎样购票更划算。

通过以上三道练习题，学生在对最优方案必要条件的分析、方案的比较、方案确定的思考中，更好地感受了优化思想，提升了解决问题的能力。

（浙江省宁波市奉化区岳林中心小学）