突破学习困惑 发展核心素养

余功学

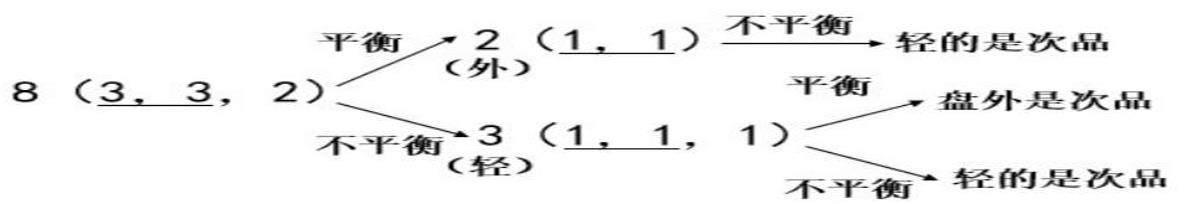
“找次品”是人教版数学五年级下册“数学广角”的内容，旨在让学生通过“找次品”活动，学会运用猜测、推理、归纳等方式分析问题并解决问题，经历由策略多样化到优化的思维进阶过程，体会优化思想。教学中，教师如何设计更具探索性的“找次品”操作活动？如何引导学生在解决问题的多样化方案中找出最优方案，并借助符号简洁地记录方案？如何让学生树立用数学思想解决实际问题的意识，提高解决问题的能力？本期，我们讨论如何更好地教学“找次品”。

“找次品”数学问题的解决策略很多，具有较强的探究性，蕴含着优化、推理、模型和转化等数学思想。教师如何采取不同的教学策略，帮助学生化解学习困惑呢？

一、理解题意，激发探究欲望

理解“至少称几次才能保证找出次品”是“找次品”教学的难点。教学中，教师可以设计生活中的实例，让学生在猜次数的过程中发现问题，准确理解题目中“至少”“保证”的含义。

教学伊始，教师出示例题：“现有81个球，其中只有1个球比其他球稍轻。如果只能利用没有砝码的天平来称，至少要称几次才能保证找到稍轻的次品？”教师先让学生猜猜可能的次数，学生给出不同的答案：最少称1次，但不能保证找到，稱80次能保证找到，但称的次数太多。怎样在“保证”找到稍轻的次品前提下，使称的次数最少呢？教师引导：81个球数量太多了，我们研究复杂问题时通常如何做？学生自然地想到“化繁为简”，即在数量小的情况下进行研究。

二、初步感知，明确解题原理

用没有砝码的天平从3个球中找次品，是“找次品”问题最基本的模型。这种模型有利于学生明确找次品的基本思路——用天平找次品，并不是一定要通过天平称，还可以利用天平的平衡原理进行推理，从而确定次品。

课堂上，教师首先通过演示操作从2个球中找轻的次品，让学生了解天平的使用方法，再让学生把称的过程简单地表示出来，学生做如下总结：用一组数如（1，1）表示物品的分组，画天平简图表示称重的结果。教师适时板书称的过程和结果“2（1，1）不平衡→轻的是次品”，简洁、清晰地表示天平上球的数量，让学生的思维过程具象化，为后面的探索活动做铺垫。接着，教师让学生研究从3个球中找次品，至少称几次能保证找出轻的次品。学生画图分析问题后汇报。一名学生回答：“在天平的左右两边各放一个球，如果不平衡，轻的那边就是次品，如果平衡，就拿下一个球，换上另一个球再称，哪边轻，哪边就是次品，一共要称两次。”另一名学生补充：“天平平衡的时候，说明天平两边放的都不是次品，这时次品一定是天平外的球，只称一次就够了。”随后，学生在教师引导下发现：用没有砝码的天平找次品，次品有可能在左边的盘子，有可能在右边的盘子，还有可能在天平外。教师进一步引导：这样看来，我们可以认为此时的天平有3个“盘子”，每称一次，我们可以判断出3个盘子中有没有次品，其中天平外“盘子”中的情况是通过推理来判断的。

通过研究从3个球中找次品，学生感受到天平可以“称一判三”，为后面理解“三分法”打下了基础，积累了活动经验。

三、比较优化，寻找最优策略

找次品时，为什么要把物品分成3份，分成怎样的3份才能最快找到次品？从8个球中找次品有多种思路与方法，教师可利用这个素材引导学生探究，从多样化的策略中寻找最优方法。

教材把例题从探索9个物体改为探索8个物体，是因为9个物体不可能分成2份来称，而学生一般会习惯性地想到将8个物体平均分成2份（4，4），称的思考过程可以这样表示：8（4，4）不平衡→（2，2）不平衡→（1，1），轻的是次品，需要称3次。学生还会出现多种不同的分法，如8（2，2，2，2）、8（3，3，1，1）等。教师要着重引导学生对8（2，2，2，2）的分法进行分析，让学生认识到把其中两份分别放到天平左盘、右盘中称时，剩下的两份都在天平外，相当于一个整体，可以只看作一份。通过师生交流，学生明白了利用天平找次品，无论分成3份、4份，还是5份，本质上都是分成3份（天平左盘、天平右盘和天平外），是天平本身的结构决定了用天平找次品分成3份更具优势。

学生借助棋子辅助思考，采用画一画的方式，分小组探究出不同的找次品方法，并简要地记录了思考过程。教师根据学生汇报的不同方法和称的次数，板书不同的思考过程。接着，教师引导：“为什么分成3份时称的次数最少呢？我们比较这四种分法［8（4，4）；8（2，2，4）；8（1，1，6）；8（3，3，2）］，第一次称完后，到底最多从几个球中找次品？你有什么发现？”学生讨论交流后汇报：“把8个球平均分成2份（4，4）称，称一次后将次品范围缩小到4个，把8个球分成3份（3，3，2）称，称一次后，无论是否平衡，最多将次品范围缩小到3个。”教师继续提问：“为什么分成2份（4，4）比分成3份（3，3，2）称的次数要多？你有什么发现？”学生回答：“分成2份，就是‘称一判二，从剩下4个中再找次品；而分成3份，利用天平左边、右边、外边三个位置找次品，就能达到‘称一判三的效果，只需要从剩下的3个中再找次品，这样就能尽快找到次品，所以要把物品分成3份。”教师追问：“分3份的方法不止一种，‘（2，2，4）、（1，1，6）、（3，3，2）都是分3份，为什么（3，3，2）是称的次数最少的分法呢？”学生回答：“按照最不利的情况考虑，次品在数量最多的那一份中，应该让数量最多的那一份尽量少，也就是要平均分，如果不能平均分，就尽可能平均分，使每一份相差最少。”最后，教师引导学生总结最优方法——分组时，应分成3份，而且要尽量平均分，并梳理出如下流程图。

以上教学，从“称一判二”到“称一判三”，从方案的多样化到优化，学生经历了分析和解决问题的过程，运用基本的逻辑推理和化归思想从多种方案中找到了解决这类问题的最优方案。

四、巩固强化，应用最优策略

明确了找次品的最优解题策略之后，利用发现的结论研究如何在9个、10个和11个球中找次品，有利于学生巩固、验证最优方案。

教师把例题分别改成从9个、10个和11个球中找轻的次品，至少称几次能保证找到次品。学生利用前面总结出的方法可以顺利地把9个球分成（3，3，3），称2次找到次品；10个球不能平均分成3份，学生就尽量使各份相差最少，分成（3，3，4），考虑最不利的情况，次品在4个球的那一份，还需要称2次，一共需要称3次；同理，11个球可以分成（4，4，3），也需要称3次。

接着，教师出示教学伊始的例题并提问：“你们现在能回答至少需要几次称找到次品吗？具体怎样称？”学生回答：“要称4次才能找出次品。将81分成（27，27，27），称第一次，问题转化为从27个球中找1个次品；将27分成（9，9，9），称第二次，问题转化为从9个球中找1个次品；前面已经知道从9个球中找1个次品要称2次，所以，从81个球中找1个稍轻的次品至少要称4次。

（作者单位：华中师范大学附属小学桂子山校区）

责任编辑  张敏