质量体积双约束下车辆装载与配送路径联合优化研究

任宗伟，钱志军，郑玮，蒲炜，张宁，祁彬彬

质量体积双约束下车辆装载与配送路径联合优化研究

任宗伟1*，钱志军2，郑玮2，蒲炜3，张宁3，祁彬彬2

（1.哈尔滨商业大学 管理学院，哈尔滨 150028；2.昆仑数智科技有限责任公司，北京 100000； 3.中国石油天然气股份有限公司河北销售分公司，石家庄 050000）

针对质量与体积共同限制的配送路径问题，综合考虑订单不可拆分、货物的体积等约束，构建包含路径最短和装载率最高双目标的车辆装载与配送路径联合优化模型。在车辆路径优化模型的求解方面，首先利用聚类算法对配送区域进行划分，然后通过车辆的载质量判断是否能进行站点货物的配送，最后利用遗传算法求得最优路径。在三维装载模型的求解上使用贪心算法和基于块的启发式算法，解决了货物的装箱问题。基于某公司具体实例对模型与算法的可行性进行了验证，优化后配送的车辆减少了1辆，配送距离减少了154.247 km，平均装载率达到了93.89%，节省了企业的配送成本。所构建的模型以及求解的算法可以提高装载率和配送效率，为解决车辆装载与配送路径联合优化问题提供理论依据。

路径优化；遗传算法；三维装载；基于块的启发式算法

根据2022年的最新通报，我国物流受疫情影响态势逐渐减小，现已逐渐恢复，社会物流逐渐增长。其中在运输方面为9.55万亿元，由此可见运输在人们的日常生活中占有很大的比重。随着经济的快速发展，配送占领着重要的地位，在配送形式、配送路径、配送时间等方面都要进行具体合理的安排与规划。但大多数的企业或物流公司尚未形成完整的配送体系，运输、仓储、销售等都存在极大的问题，深深地影响着企业的发展。想要降低企业的运输成本，促进企业的发展，其中一个重要的措施是合理规划配送路径和车辆装载。现大多数企业在配送货物时仅仅依靠人为经验和货物的紧急程度进行配送，效率较低，如出现紧急情况也无法有效调动机动人员和车辆，经常容易出现纰漏，需要花费较多的人力成本和时间成本。现阶段考虑路径优化时同时考虑装箱问题的情况较少，如何在满足尽可能多的装箱基础上优化配送路径，仍然是值得研究的现实问题。

车辆路径问题（Vehicle Routing Problem，VRP）由Dantzig等[1]于1959年首次提出，现已成为运筹学中一类经典的组合优化问题。随着实际需求的不断变化，各种各样的VRP一直在出现，并不断地发展。Agárdi等[2]提出了一种通用的VRP模型，并通过案例加以证明。在解决VRP问题时，Joanna等和Olaniyi等[3-4]讨论了遗传算法解决VRP问题。容量约束的车辆路径问题（Capacitated Vehicle Routing Problem，CVRP）是车辆路径问题的拓展问题[5]，针对CVRP问题，Simensen等[6]提出了一种混合元启发式算法解决CVRP问题。梁彪等[7]提出了“一种求解CVRP问题的遗传蚁群融合算法”，为解决带容量约束的车辆路径优化问题提供了一种解决办法。针对大规模的多仓库多车型车辆路径问题（Multi-Depot Heterogeneous Fleet Vehicle Routing Problem，MDHFVRP），多数研究采取先聚类再优化的求解思路，此种方法可以缩小问题规模和降低求解难度。例如，Thangiah等[8]利用遗传算法进行客户分群，将问题转变为旅行商问题，然后通过插入启发式算法求解旅行商问题。Luo等[9]则改进了蛙跳算法，对客户聚类后再进行优化，然后对总体进行调整以生成新的聚类，直到满足设定的收敛标准为止，该方法被证明可以用来求解大规模的多车场车辆路径问题。

针对三维装载问题，王超等[10]提出三维装载与CVRP联合多目标优化问题（3LCVRPMO）模型，该模型在三维装载约束下，CVRP问题（3LCVRP）的基础上，考虑了配送车辆数目及路径总距离2个目标函数，在权衡装箱和路径优化2个优化过程的基础上，构建了多阶段/两层混合算法架构（MSOTLH）及其算法，并对路径优化偏好的3LCVRPMO问题进行求解。那日萨等[11]针对7种现实约束的集装箱三维多箱异构货物装载优化问题，提出了一种基于“块”和“空间”的启发式搜索算法，并基于Net平台开发了一款3D装箱布局优化可视化软件，已在相关物流企业中得到推广应用，验证了算法的实用性。多数学者通过先聚类后装载来提升车辆的装载率[12-13]，为三维装载约束下的路径优化提供了决策参考和方法支持。王勇等[14]设计了集成k-means时空聚类的Clarke-Wright-非支配排序遗传算法，为求解三维装载路径优化问题提供了方法。崔会芬等[15]探讨了三维装箱约束下的车辆路径优化问题，引入多种约束，采用遗传算法进行求解，提高了物流配送效率，降低了配送成本。

本文在车辆路径优化模型的基础上增加三维装载约束限制，考虑带三维装载的路径优化模型，建立质量体积双约束的路径优化模型以及车辆的三维装载模型，并结合具体实例对模型和算法的可行性进行分析。利用聚类算法对站点进行分区，在遗传算法求解过程中调用求解三维装载的贪心算法和基于块的启发式算法，统筹进行三维装载和规划路径。

1 问题描述

首先已知配送中心和各个配送站点的位置信息、各个站点的需求量信息，其中配送中心有一定数量的车可用于配送，同时配送中心只有一种车型用于配送；已知车辆的载质量和容量，在配送过程中每个车次所走路线装载的货物总质量不能超过车的最大载质量，同时每个车次所走路线装载的货物总体积不超过车辆容积，每个站点只被服务一次，在某一时刻所有负责配送的车同时从配送中心出发，分别完成各自配送任务之后回到配送中心。在车辆的装箱问题上要求把一定数量的货物放入车厢中，使得每个车厢中的货物体积之和不超过车辆容量，并使车辆数量最少。基于以上条件，设计一个最优的方案，使得车辆配送总路线最短（如图1所示）。针对该问题，建立了路径优化模型和三维装载模型，路径优化模型的目标函数为车辆行驶的总距离最短，约束条件在经典VRP问题的基础上添加车载质量约束和容量约束。三维装载模型为个直方体货箱在不相互干涉的情况下尽可能多地装入货车车厢内，使货车车厢的空间装载率最高。将三维装载模型与路径优化模型相融合，即在满足装箱约束的前提下，尽可能使车辆装更多的站点的货物，使配送车辆的总行驶距离最短，具体描述见图2。

图1 车辆配送路径问题描述

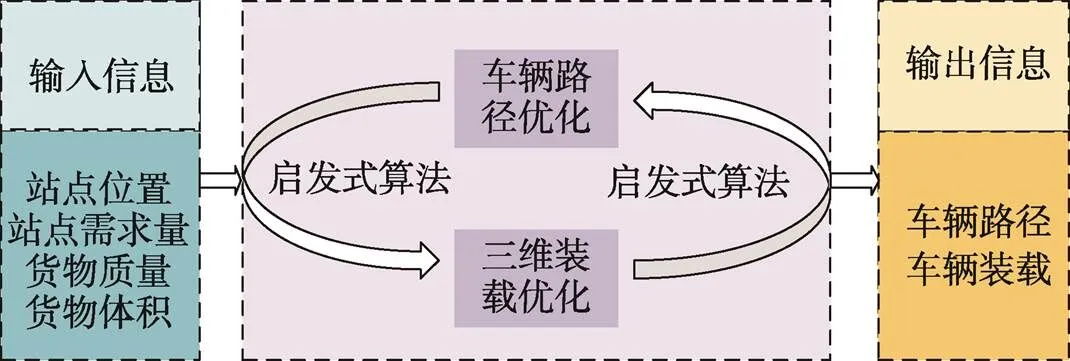
图2 车辆路径优化与三维装载相融合描述

2 数学模型的构建

2.1 模型假设

根据现有条件，本文构建的模型做出以下假设：

假设1：配送中心库存量可满足所有客户需求，且仅有一个配送中心。

假设2：配送中心只有一种车型的车，车辆数足够完成配送任务。

假设3：车辆从配送中心出发，完成配送任务后再返回配送中心。

假设4：客户的需求不可分割，每个客户只能被一辆车服务，且只能被服务一次。

假设5：所有的客户位置已知，车辆都可以配送到。

假设6：配送车辆只承担送货任务，不承担取货，配送完成后车辆返回配送中心。

假设7：配送车辆在路上不存在交通拥堵情况。

假设8：所有车辆的实际载重不能超过其额定载重。

假设9：所有车辆的实际载货体积不能超过其额定容积。

假设10：客户需求是静态的，确定后将不会发生改变。

假设11：不考虑单个客户的需求量多于一辆车的最大载质量的情况。

假设12：不考虑单个客户的需求货物体积大于一辆车的最大容积的情况。

假设13：货物都是规则物体。

假设14：货箱必须放置在车厢内部，不能够超出车辆的边界范围。

假设15：货箱的长宽高和质量信息都是已知的。

假设16：实际装载过程中货箱与货箱之间的装载间隙忽略或者可以看作车厢在计算空间的时候已经预留一部分作为装载间隙。

假设17：货箱不会由于堆积而产生变形，不是危险品等特殊货物。

2.2 参数说明

本文建立的模型中所有参数说明如下。

2.3 模型的构建

2.3.1 路径优化模型

数学模型建立如下：

目标函数：

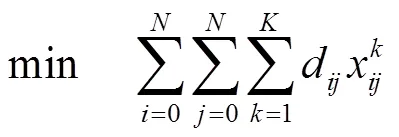
约束条件：

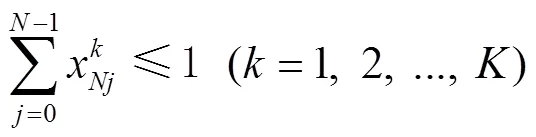
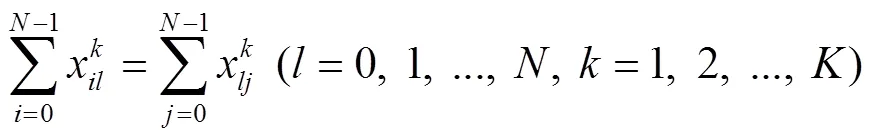
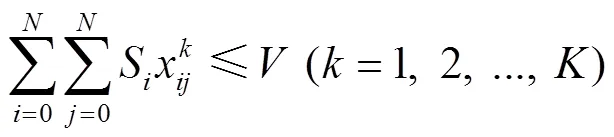
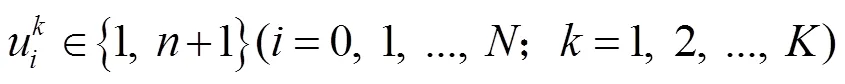
2.3.2 三维装载模型

数学模型建立如下。

目标函数：

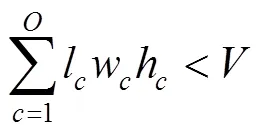
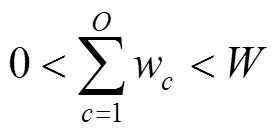
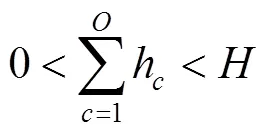
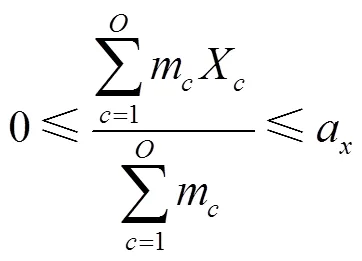
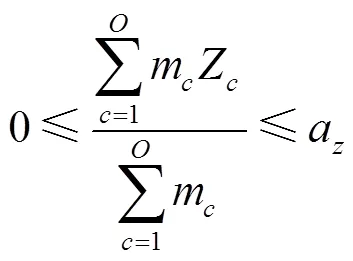
式（12）为车厢体积利用率最优，即在货车车厢中对要装入的货箱1,2,3, ...,P寻找一个合适的货物装载顺序，使得装入的货箱体积最大，车厢的剩余空间最小；式（13）表示货箱总体积约束；式（14）、式（15）、式（16）表示货箱三维尺寸长宽高约束；式（17）表示货物总质量约束；式（18）、式（19）、式（20）表示集装箱装满货物后的重心范围约束；式（21）表示货物 “先进后出”的约束。

3 算法实现

在总体方案设计按照车辆路径优化和三维装载优化2个任务开展研究。车辆路径优化方面，在考虑车型种类、商品质量和体积的基础之上构建优化模型；在三维装载优化中主要考虑的因素包括配送顺序、体积、三维旋转、质量等。2个任务的求解算法以元启发式算法为主。框架如图3所示。

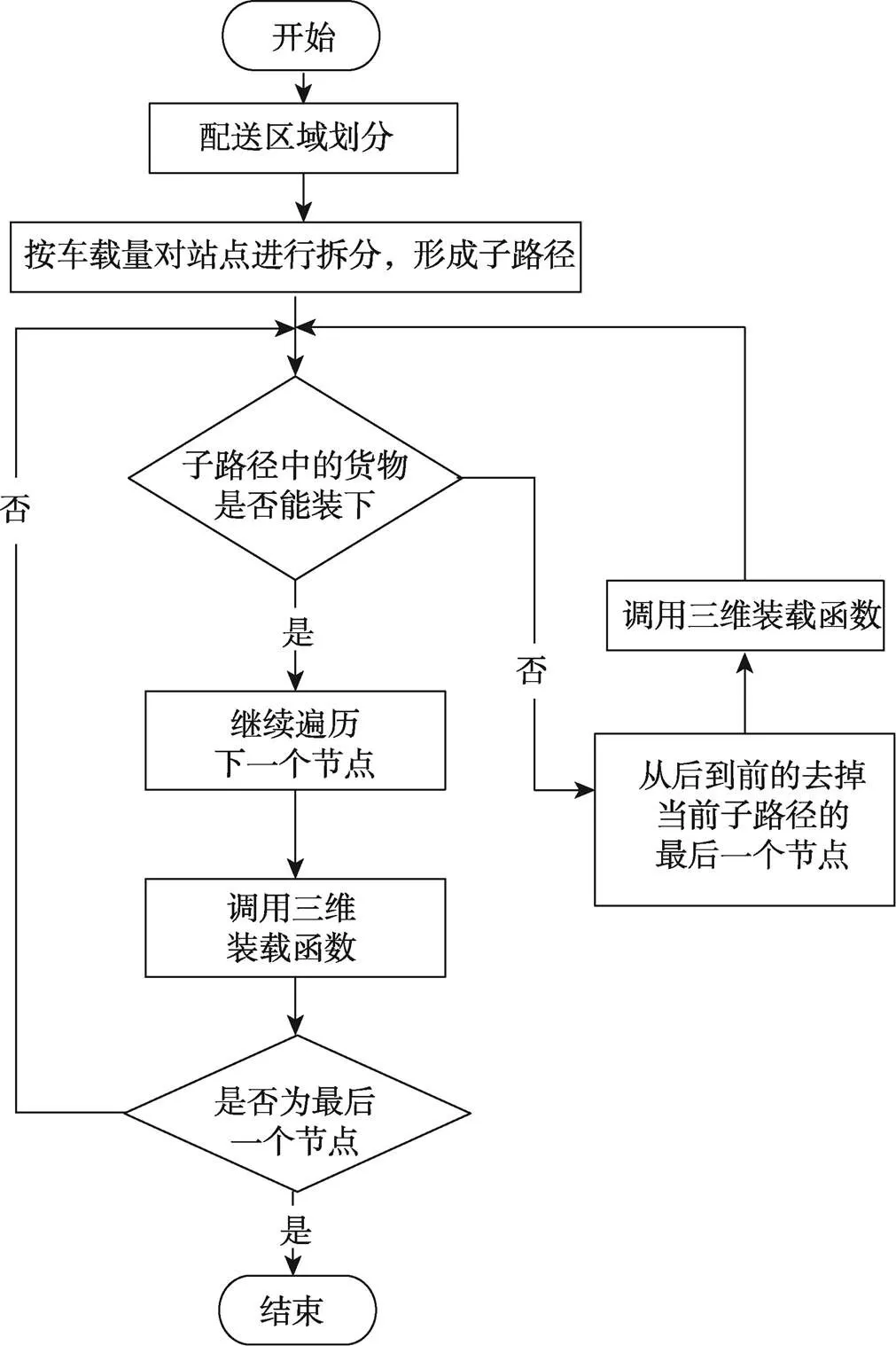
图3 技术方案的设计框架

3.1 路径优化算法

3.1.1 路径优化模型

为使路径规划达到最优，配送区域划分不仅可以节约资源，避免不必要的资源浪费，还可以更好地满足顾客的需求，及时高效地完成配送计划。配送区域划分是根据临近原则实施的，目的就是配送达到省时、省事、省力，给予顾客最优的体验，满足顾客最大的需求。为此在解决路径优化问题时先使用聚类算法。K-Means聚类算法是一种迭代求解的聚类分析算法，其主要步骤如下：

1）选取个对象作为初始的聚类中心。

2）计算每个对象与各个种子聚类中心之间的距离，把每个对象分配给距离它最近的聚类中心。利用K-means聚类算法的特点依据任意便利店的经纬度坐标进行聚类，对配送区域进行划分，以得到最优的配送区域划分。

本文主要运用平均轮廓系数法来求取最优的值。平均轮廓系数法衡量了聚类结果的质量，即衡量每个点被放到当前类簇有多合适，平均轮廓系数很高意味着聚类的结果很好。这种方法计算不同值下所有点的平均轮廓系数，能够使平均轮廓系数最大的就是最优的类簇数量。

3.1.2 遗传算法

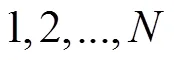
2）适应度的好坏直接影响着染色体的选择，因文中的目标函数为车辆行驶总距离最短，故设定的适应度函数是目标函数最大值与当前目标函数值的差值，当前目标函数值越小，差值越大，则适应度值越大，染色体越好。

3）染色体的选择、交叉、变异也会影响遗传算法的结果。在染色体选择方面，使用了二元锦标赛法进行选择，通过随机选择2个个体，将适应度值好的留下，重复多次，直至选择的种群规模达到预先设定的值。

4）交叉方面选择了OX交叉法进行交叉，在程序编写中，从种群中随机选择2个父代后，再随机选择2个交叉点，将父代的中间部分交叉生成子代。交叉后的子代会被添加到模型的解列表中，直到解的数量达到种群数量为止。

5）染色体的变异选择了二元突变，随机选择2个交换位置。通过对染色体交叉、变异概率的改变，可以实现遗传算法的优化。

将聚类算法与遗传算法融合后的流程如图4所示。

图4 路径规划程序流程

3.2 三维装载算法

3.2.1 贪心算法

贪心算法主要是在某种意义上的局部最优解。在三维装载的设计上，对于装载，首先将货物按站点分类，一个站点的所有货箱是一个箱子列表BoxList，每个箱子列表中所有的箱子都按照尺寸大小进行分类，并在每一类里进行质量降序，以便后续同种货物或同等大小的箱子进行集中装载。在装载前需要计算货车3个方向能放置的最大货箱个数，判断货箱个数是否小于方向可放置个数，若小于则优先方向放置货箱，否则判断货箱个数是否小于×方向可放置个数，若小于则优先×方向放置货箱，否则优先××方向放置货箱，以此优先选择体积最大且宽最大的块为最优块chosen。

3.2.2 基于块装载的启发式优化算法

简单块是由同一朝向的同种类型的箱子堆叠而成的，箱子和箱子之间没有空隙，堆叠的结果必须正好形成一个长方体，其生成必须满足3个条件：简单块的长宽高必须在集装箱的体积范围内；简单块的质量必须在集装箱的承受范围内；简单块使用的箱子数量必须符合该类箱子的剩余数量。

在每个装载阶段中根据剩余空间大小计算能使用的所有块，然后从中选择一个块装入剩余空间，这样在装载时不会考虑重心约束的条件。已知由贪心算法选出最优块后，再判断是否能放入Space空间。若可以放下，将块放入并标记货箱的位置，插入第1块箱子后，每插入一个块都有3个Space空间，并且每插入一个块都更新空间列表，对每个块都可以按照轴旋转，所有货箱的重叠部分是需要判断的，以免出现悬空现象；若不能放下就判断是否超过oversize的20%，若超过oversize的20%就判断是否能放下单个货箱，若不能放置就舍弃该空间，将货箱放入备用空间，若能放下，判断目标货箱放置的位置是否可能被后面的货物所遮挡，若被遮挡则舍弃该空间，将货箱放入备用空间，否则放置货箱并标记货箱的位置。最后判断是否为BoxList类里面的最后一个货箱，若不是就循环BoxList类里面的货箱，若是就判断是否为BoxList列表里面的最后一个类，若不是就循环BoxList列表，若是就判断是否为最后一个站点，若不是就循环站点，若是就判断是否能全部放入货车，如果可以放置就返回货车已装载的箱子具体位置和装载率，如果不能就舍弃当前站点，再返回路径规划重新寻找可以再装载的站点。重复上述步骤直至所有站点都可以装载完成，返回最终车次。

将贪心算法与基于块装载的启发式优化算法相结合后，具体装载流程如图5所示。

4 算法实例

本文以某连锁便利店为例进行研究。该连锁店共148个站点。配送中心负责向各个便利店运送所需货物，部分站点的信息如表1所示。通过对连锁便利店的现状进行分析，发现在运输过程中存在行驶道路迂回等情况，配送时人为因素干预较大，由人工随机配送。根据订单表中的日期筛选订单，根据位置信息数据找到收货人名对应的发货地编码，按某一天的车次和客户单号编号顺序计算当前车次的行驶距离，如表2所示。

对148个站点地理位置进行聚类，利用平均轮廓系数法求解的结果如图6所示。由此可得，当聚类数=5时最优，最终148个站点共分为五部分。

将站点聚类后，利用遗传算法进行求解，设车辆的最大载质量为5 t，用于配送的车辆足够多，考虑货物的体积时，基本参数设置如表3所示，迭代500次，得出的结果如图7所示，运行时间及运行结果如表4所示。同理，使用另外3种启发式算法进行求解。4种算法的基本参数设置如表3所示，设车辆的最大载质量为5 t，用于配送的车辆足够多，考虑货物的体积时，迭代500次的运行结果如图7所示，运行时间及运行结果如表4所示。

图5 装箱算法流程

表1 部分站点的坐标

Tab.1 Coordinates of some sites

表2 车辆配送初始数据

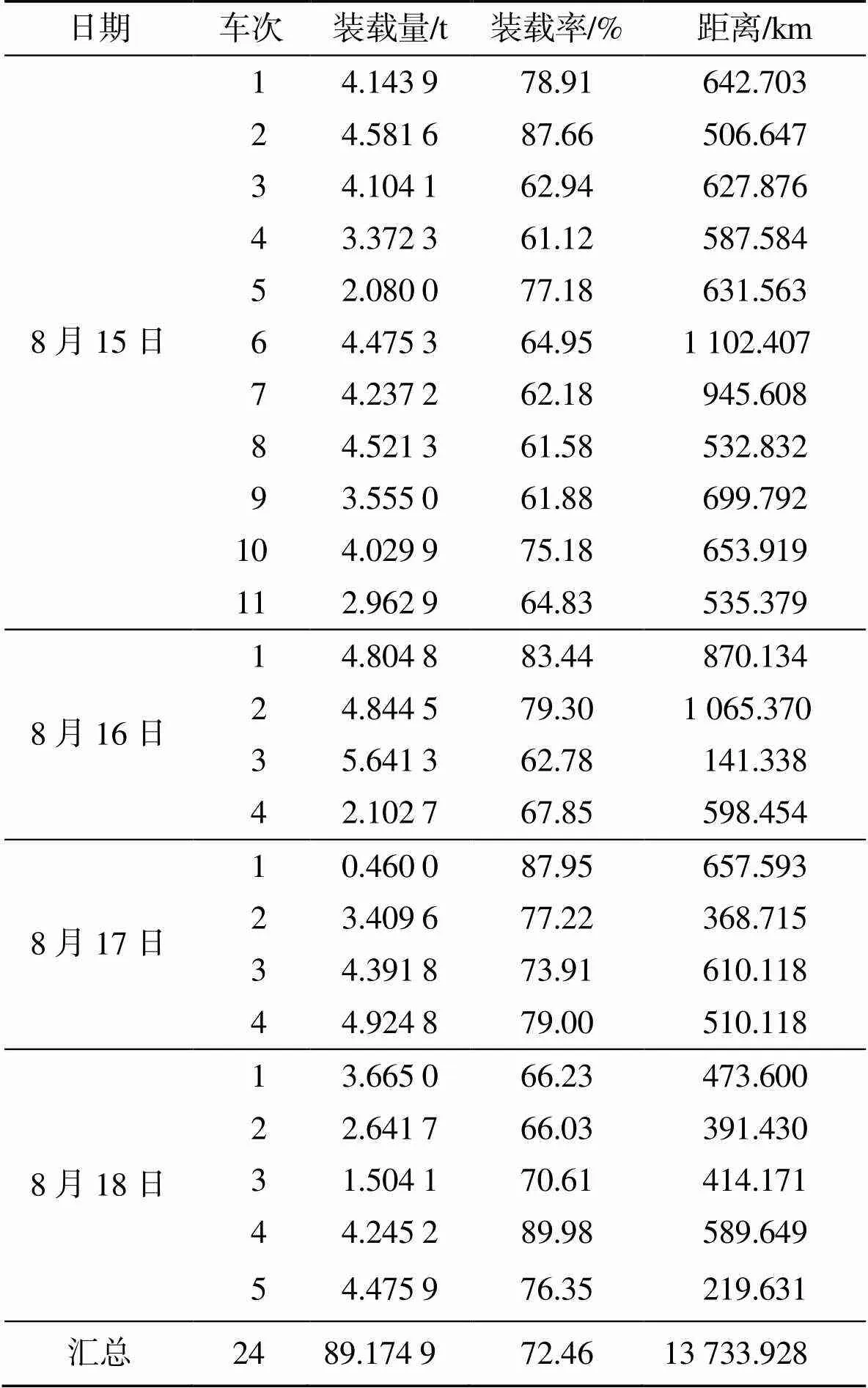
Tab.2 Initial data of vehicle delivery

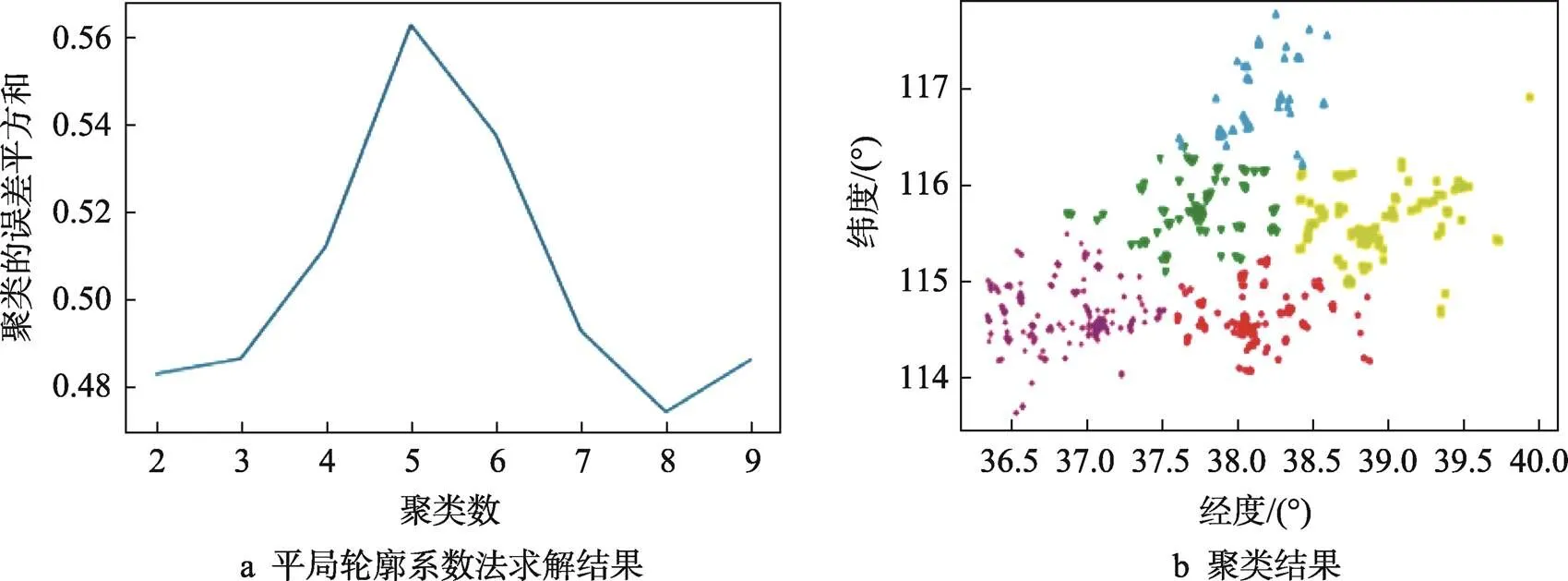
图6 站点聚类结果

表3 4种启发式算法参数说明

Tab.3 Parameters explanation of four heuristic algorithms

图7 各算法迭代图

通过对比4种算法的迭代图，可以发现禁忌搜索算法和蚁群算法过早收敛的现象较为明显，粒子群算法也有轻微的陷入局部最优的情况，而遗传算法一直在向全局最优的结果收敛，虽然最后没有稳定在某一个数值，但是比其他3种算法更优。

表4 4种启发式算法运行结果

Tab.4 Running results of four heuristic algorithms

由表4对比分析，发现遗传算法计算出的车次数和路线距离都更为理想，故后续程序设计时采用遗传算法对构建的模型进行求解。

表5 4种启发式算法性能分析

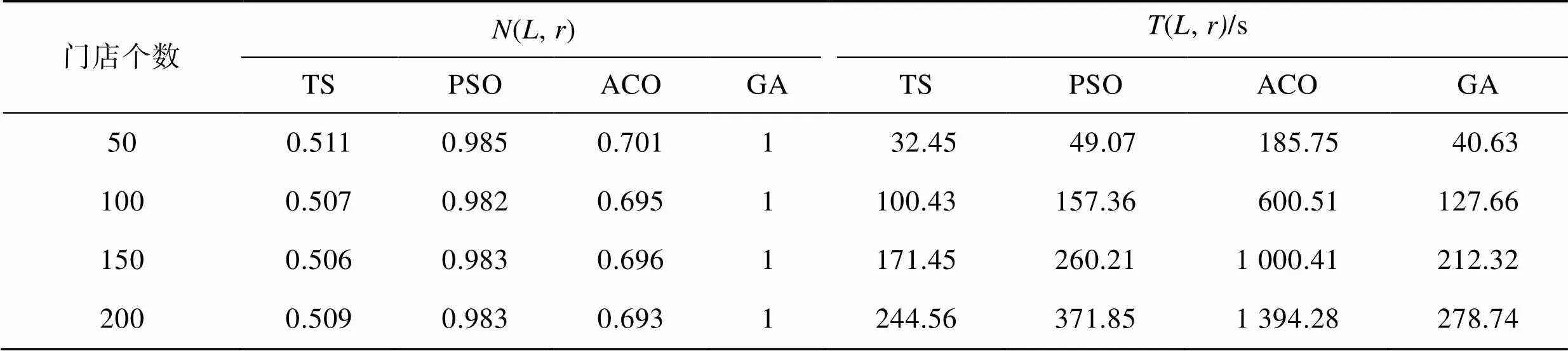
Tab.5 Performance analysis of four heuristic algorithms

由表5可知，随着求解规模的变大，遗传算法在性能参数和运行时间方面优势更加明显。采取不同的交叉、变异概率进行求解，所求解的行驶车次数均为23辆，具体的路线距离结果如表6所示。

表6 遗传算法优化结果

Tab.6 Genetic algorithm optimization results

由表6可知，当交叉概率为0.8，变异概率为0.2时，路线距离最短。

取车辆的最大载质量为5 t，将企业的初始数据利用路径优化算法与三维装载算法优化后形成的配送路线结果如表7所示，配送路径如图8所示。

4种优化算法与三维装载算法相结合形成的三维装载部分展示如图9所示。表8展示了优化前后相关优化结果的变化情况，其中优化前指人工随机配送的结果，优化后指利用遗传算法为主的路径优化算法和三维装载算法的优化结果。

表7 优化结果

Tab.7 Optimal results

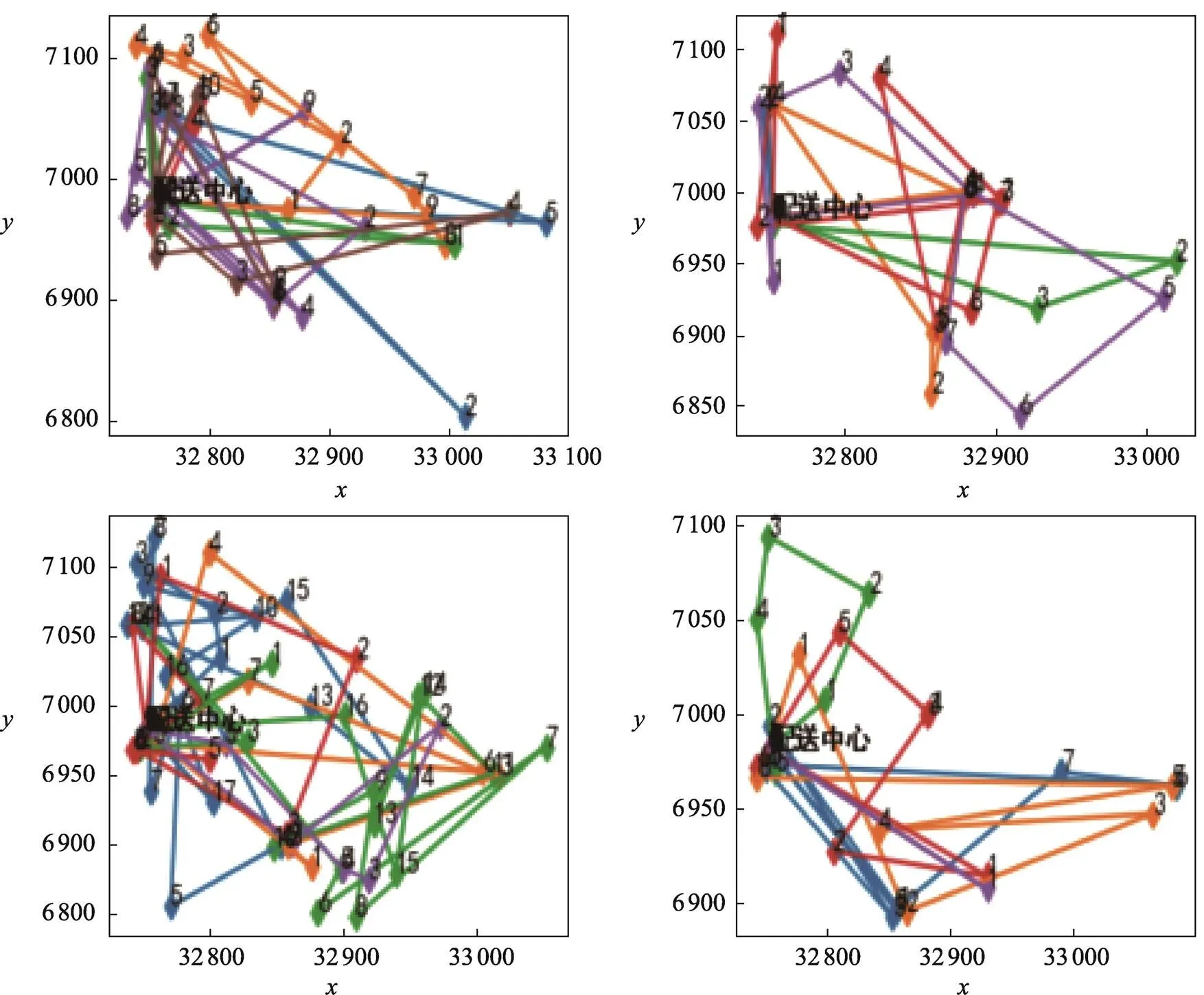
图8 优化后的路线结果

图9 三维装载展示

表8 优化前后相关结果对比

Tab.8 Comparison of relevant results before and after optimization

优化后的车辆配送区间更加聚集，由图10可以看出遗传算法求解的装载率最高。由表8可知，优化前后结果对比，配送的车辆减少了1辆，配送距离减少了154.247 km，使用聚类算法、遗传算法、贪心算法、基于块的启发式算法4种算法相结合的方式，使得车辆达到了较高的装载率，平均装载率达到了93.89%，节省了企业的配送成本。

5 结语

配送路径与连锁便利店的生产经营有着密不可分的关系。本文根据存在的单一车型考虑质量与体积的配送路径问题，建立了相应的路径优化模型与三维装载模型，并利用聚类算法和遗传算法进行解决，在遗传算法求解过程中调用解决三维装载的贪心算法与基于块的启发式算法，通过前后对比发现该算法降低了车辆的使用数量，车辆的装载率较高，为便利店节省了配送成本，优化的结果科学合理。

在算法的求解过程中还存在不足之处，未来三维装载关于货物的承重、货物的重心与平衡以及如何优化货物的装载效率和装载时间仍需继续研究，进一步完善三维装载的程序代码，实现高效装载。

[1] DANTZIG G B，RAMSER J H. The Truck Dispatching Problem[J]. Management Science, 1959, 6(1): 80-91.

[2] AGÁRDI A, KOVÁCS L, BÁNYAI T. Mathematical Model for the Generalized VRP Model[J]. Sustainability, 2022, 14(18): 1639.

[3] JOANNA O, ANETA P, WITOLD M. Selected Genetic Algorithms for Vehicle Routing Problem Solving[J]. Electronics, 2021, 10(24): 3147.

[4] OLANIYI O S, JAMES A K, IBRAHIM A A, et al. On the Application of a Modified Genetic Algorithm for Solving Vehicle Routing Problems with Time Windows and Split Delivery[J]. IAENG International Journal of Applied Mathematics, 2022, 52(1): 1-9.

[5] 靳康飞, 闫军, 梁云涛. 容量约束的车辆路径问题研究现状综述[J]. 甘肃科技纵横, 2022, 51(10): 52-56.

JIN K F, YAN J, LIANG Y T. A Review of the Current State of Research on the Capacited Vehicle Routing Problems[J]. Scientific & Technical Information of Gansu, 2022, 51(10): 52-56.

[6] SIMENSEN M, HASLE G, STÅLHANE M. Combining Hybrid Genetic Search with Ruin-and-Recreate for Solving the Capacitated Vehicle Routing Problem[J]. Journal of Heuristics, 2022, 28(5): 653-697.

[7] 梁彪, 严昌龙. 一种求解CVRP问题的遗传蚁群融合算法[J]. 中国物流与采购, 2021(24): 34-35.

LIANG B, YAN C L. A Genetic Ant Colony Fusion Algorithm for Solving CVRP Problems[J]. China Logistics & Purchasing, 2021(24): 34-35.

[8] THANGIAH S R, SALHI S. Genetic Clustering: An Adaptive Heuristic for the Multidepot Vehicle Routing Problem[J]. Applied Artificial Intelligence, 2001, 15(4): 361-383.

[9] LUO J, CHEN M R. Multi-Phase Modified Shuffled Frog Leaping Algorithm with Extremal Optimization for the MDVRP and the MDVRPTW[J]. Computers & Industrial Engineering, 2014, 72: 84-97.

[10] 王超, 金淳, 韩庆平. 三维装载与CVRP联合多目标优化问题的模型及算法[J]. 控制与决策, 2016, 31(5): 929-934.

WANG C, JIN C, HAN Q P. Model and Algorithm for Multi-Objective Joint Optimization of Three-Dimensional Loading and CVRP[J]. Control and Decision, 2016, 31(5): 929-934.

[11] 那日萨, 韩琪玮, 林正奎. 三维多箱异构货物装载优化及其可视化[J]. 运筹与管理, 2015, 24(4): 76-82.

NA R S, HAN Q W, LIN Z K. Optimization and Visualization of Multiple 3 D Container Loading Problem with Non-Identical Items[J]. Operations Research and Management Science, 2015, 24(4): 76-82.

[12] YAN X X, WANG G R, JIANG K S, et al. Multi-Objective Scheduling Strategy of Mine Transportation Robot Based on Three-Dimensional Loading Constraint[J]. Minerals, 2023, 13(3): 431.

[13] LIU Y, YUE Z C, WANG Y, et al. Logistics Distribution Vehicle Routing Problem with Time Window under Pallet 3D Loading Constraint[J]. Sustainability, 2023, 15(4): 3594.

[14] 王勇, 魏远晗, 蒋琼, 等. 三维装载约束下基于运输资源共享的车辆路径问题[J]. 计算机集成制造系统, 2023, 29(9): 3153-3170.

WANG Y, WEI Y H, JIANG Q, et al. Vehicle Routing Problem Based on Transportation Resource Sharing under Three-Dimensional Loading Constraints[J]. Computer Integrated Manufacturing Systems, 2023, 29(9): 3153-3170.

[15] 崔会芬, 许佳瑜, 杨京帅, 等. 基于遗传算法的3L-CVRP优化问题研究[J]. 交通信息与安全, 2018, 36(5): 124-131.

CUI H F, XU J Y, YANG J S, et al. An Optimization of 3L-CVRP Based on a Genetic Algorithm[J]. Journal of Transport Information and Safety, 2018, 36(5): 124-131.

Joint Optimization of Vehicle Loading and Distribution Routes under Dual Constraints of Quality and Volume

REN Zongwei1*, QIAN Zhijun2, ZHENG Wei2, PU Wei3, ZHANG Ning3,QI Binbin2

(1. School of Management, Harbin University of Commerce, Harbin 150028, China; 2. Kunlun Digital Intelligence Technology Co., Ltd., Beijing 100000, China; 3. China National Petroleum Corporation Hebei Sales Branch, Shijiazhuang 050000, China)

The work aims to constructa joint optimization model for vehicle loading and distribution routes with the shortest route and the highest loading rate, taking into account constraints such as the indivisibility of orders and the volume of goods, so as to address the delivery route problem with common limitations of quality and volume. In terms of solving the vehicle route optimization model, first the clustering algorithm was used to partition the distribution area, and then the load capacity of the vehicle was used to determine whether the station goods could be delivered. Finally, the genetic algorithm was used to obtain the optimal route. The greedy algorithm and the block based heuristic algorithm were used to solve the loading problem of goods in the 3D loading model. The feasibility of the model and the algorithm was verified based on a specific example of a company. After optimization, the number of vehicles for delivery was reduced by 1, the delivery distance was reduced by 154.247 km, and the average loading rate reached 93.89%, saving the company's delivery costs. The results indicate that the constructed model and the solved algorithm can improve loading rate and delivery efficiency, providing a theoretical basis for solving the joint optimization problem of vehicle loading and distribution routes.

route optimization; genetic algorithm; 3D loading; block based heuristic algorithm

TB485.3；F540

A

1001-3563(2024)09-0232-11

10.19554/j.cnki.1001-3563.2024.09.030

2023-10-20

国家自然科学基金（71371061）；国家重点研发计划（2018YFB1402500）；黑龙江省哲学社会科学资助项目（23RKB134）；黑龙江省自然科学基金项目（LH2023G009）