参与电网削峰调节的电动重卡换电站调度策略
2024-05-18郭春林高泽阳赵炳卓海晓涛
程 飞,郭春林,高泽阳,赵炳卓,海晓涛,曹 曦
(1.华北电力大学电气与电子工程学院,北京市 102206;2.国网商用电动汽车投资有限责任公司,北京市 100071)
0 引言
在“碳达峰·碳中和”目标政策的驱动下,电动汽车(electric vehicle,EV)产业迅猛发展[1-2]。换电作为电动汽车补能的重要方式之一,具有高效、迅速、安全的特点[3-6]。因重型卡车(简称重卡)在货车排放量中占比巨大,倾向于采用换电补能的电动重卡正在其中加速渗透,随之而来的是电动重卡换电站的规模化建设[7-8]。与此同时,电网调峰压力也随着电动汽车渗透率的增大而增大[9-10],而换电站通过集中有序的充电管理,可以参与电网的削峰调节[11],规模化的电动重卡换电站将成为电网削峰调节不可忽视的调度资源。
目前,国内外学者已经对以减小系统负荷峰谷差为目标的换电站电池调度策略开展了研究。文献[12]基于排队论构建了有序充电模型,通过控制充电电池的数量实现填谷;文献[13]提出了基于带基线的蒙特卡洛策略梯度法的换电站实时调度策略,用于优化换电站的充放电调度及响应电池数量,实现了削峰填谷;文献[14]建立了有序充电方式下的电池冗余模型,减小了电网峰谷差,增加了电池冗余度;文献[15]基于分区电池控制方法,提出了一种电池调度策略,用于在满足换电需求的同时利用剩余电池参与削峰填谷;文献[16]提出了通过价格激励引导换电站在服务能力约束前提下参与配电网负荷削峰的方法。但是,上述文献的调度策略均只考虑控制电池的充电数量,未考虑控制电池的充电功率。
另外,也有部分研究同时考虑了电池充电数量和充电功率:文献[17]提出以削峰填谷为目标的充放电策略,提高了全网风电消纳能力;文献[18]通过两阶段调度模型,实现了换电站参与风电消纳和电网削峰填谷;文献[19]建立了换电站日前调度与实时调度模型,最大化换电站收益并实现削峰填谷,但该文章认为乏电与满电电池只能在下一个时段参与充换电行为,与实际情况相差较大。
综上所述,文献[12-19]均基于换电站内配有大量电池、采用慢充充电或换电需求易于精准预测的场景。而电动重卡换电站因电动重卡高随机、高突发性的工作任务,难以实现换电需求的精确预测,又因站内电池数量少,预测偏差在调度中带来的负面影响较大。因此,面对电动重卡换电站的运行特点,已有的换电站参与电网削峰的调度研究尚显不足。
为此,本文首先针对电动重卡的需求特性,采用实际换电站各时段的历史数据统计结果作为换电需求的预测值,提出了基于预测值的日内调度策略和实时修正策略,在保证参与削峰的同时满足换电需求;然后,建立了以削峰为目标的时间-功率计算模型,考虑充电机约束、充电时间约束、电池电量约束和站内变压器容量约束;最后,给出模型算例并使用差分算法进行求解,验证了该策略和模型的有效性。
1 换电需求预测
电动重卡因工作任务性质的原因,其换电需求在时间上的分布规律较弱。针对该问题,本章提出了换电需求的预测方法。
1.1 电动重卡换电站基本运行情况
电动重卡换电站由监控及站控仓、重卡换电工位、机器人仓、换电机器人和电池仓组成。电池仓内配备1、2 个备用充电位以及若干常用充电位,并空出1 个常用充电位作为中转充电位。其中,除用于中转以外的每个常用充电位配备1 块常用电池,每个备用充电位配备1 块备用电池,本文假定备用电池和备用充电位不参与充换电。
换电过程为:电动重卡驶入换电工位后,在监控及站控仓的监督控制下,由换电机器人将乏电电池移动至中转充电位,再从常用充电位中随机选择一个满电电池,更换到电动重卡上,最后电动重卡驶出换电工位,换电过程结束。当乏电电池被放到常用充电位上后,由监控及站控仓控制是否投入充电。电动重卡换电站结构和换电流程如图1 所示。
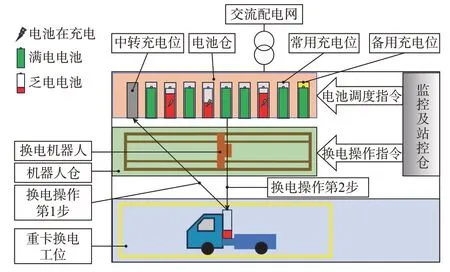
图1 电动重卡换电站结构和换电流程Fig.1 Structure and battery swapping process of battery swapping station for electric heavy-duty truck
1.2 时段划分及换电需求预测
首先,将一天24 h 划分为若干时段,时段划分步长tp(单位为分钟)如式(1)所示。
式中:WB为电池额定容量;Pce为电池额定充电功率。
划分起始点为当日零点,若当日最后一段时长小于tp,则用下一日的时间进行补全。
根据换电站面临的实际生产状况,选取合理日期范围内的历史运行数据,统计出每天各个时段的换电次数,得到各时段换电次数的众数和最大值,分别作为换电基本需求预测值和极端需求预测值,记为Np、Nm。
2 电池调度策略
目前,实际换电站采用的常规充电方式是对换下的电池立刻以额定功率进行充电,直至充满。若想使换电站实现削峰,则需对电池的充电行为进行干预,改变投入充电的电池数量以及电池的充电时间和充电功率,在满足换电需求的基础上,实现削峰效果。但是,由于电动重卡换电站的少量电池面对大量需求的配置特点,使得乏电电池的最晚充满时间受到较大限制。
针对以上问题,本章提出基于预测的日内调度策略和日内实时修正策略。
2.1 投入充电的电池分类
首先,假设换电站中常用电池总数为N,分为Nf个满电电池、Nn个不投入充电电池和Nc个充电电池。其中,Nc的表达式如式(2)所示。
式中:nc为正在充电的电池数量;nw为确定要投入充电但尚未开始充电的电池数量。
同时,本文做出如下假设:
1)电池在换电完成时即可选择是否投入充电。
2)当站内没有可供换电的电池时,司机愿意等待的最长时间为twait;当超出最长等待时间时,司机选择离开。
按照前文的时段划分,对于任意相邻的两个时段,即本时段[t,t+tp]和下一时段[t+tp,t+2tp],将本时段确定投入充电的电池分为两类:
1)第1 类电池:为满足下一时段的基本换电需求而投入充电的电池,该类电池数目记为Ncp,next。基本换电需求必须得到及时满足,则其允许充电时间范围tcp,next为:
式中:twh为本块电池换电完成时刻;Tsd,next为下一时段的开始时刻;th为电动重卡完成一次换电所需时间;Nsy,this为按照基本充电需求预测值计算所得本时段最后时刻的预计剩余满电电池数量。Nsy,this的表达式为:
式中:Nfs、Ncs分别为本时段开始时刻的满电电池数和充电电池数;Np,this为本时段的基本需求预测值。
2)第2 类电池:为满足下一时段的极端换电需求而投入充电的电池,该类电池数目记为Ncm,next。对于极端换电需求,考虑司机能够等待的时间,则其允许充电时间范围tcm,next为:
对于以上两种电池,记允许最早开始充电时间为tzz、允许最晚结束充电时间为tzw。
2.2 基于预测的日内调度策略
根据每个时段内的每次换电开始时刻和换电完成时刻的Nf、Nc,以及下一时段的基本需求预测值Np,next、极端需求预测值Nm,next制定基于预测的日内调度策略,确定换下的电池是否投入充电。若投入充电,则根据电池种类确定其允许充电时间范围。
2.2.1 紧急调度策略
1)策略1:若因设备故障、电力供应故障导致在出现换电需求时没有可供换电的电池,则使用电池荷电状态(state of charge,SOC)达到85%的电池进行换电。若全部电池的SOC 均小于85%,则选取SOC 最大的电池,将其目标SOC 值Smb确定为85%,其充电功率由本文后续提出的时间-功率计算模型确定,并待其充电至Smb后进行换电。在完成换电后,对于被换下的新乏电电池,将其划归为第1 类电池。
2)策略2:若本时段极端需求预测值Nm,this大于换电站配备的常用电池总数N,则将未投入充电的电池全部投入充电,且将本时段前Nm,this-N个换下的电池的tzw更改为t+Nth。
2.2.2 换电完成时刻调度策略
1)约束条件1:本时段剩余满电电池与第1 类电池数量之和需满足下一时段的基本换电需求预测值,即
当不满足该约束条件时,将从车上换下的新乏电电池投入充电,并划归为第1 类电池,同时将其Smb确定为100%。
2)约束条件2:本时段剩余满电电池、第1 类与第2 类电池数量之和需满足下一时段的极端换电需求预测值,即
若不满足该约束条件,则将从车上换下的电池投入充电,并将其划归为第2 类电池,且将其Smb确定为100%。
2.3 日内实时修正策略
在基于预测的日内调度策略的基础上,根据日内各时段实际换电次数对电池调度进行修正,确保至少有Nm,next块电池为下一时段的换电需求做准备。
2.3.1 电池数量调整策略
在换电完成时刻,判断本时段已经完成的换电次数Nh是否已经达到本时段的基本充电需求预测值Np,this,即
1)若此时满足式(8),则继续判断站内电池状态是否满足:
若此时不满足式(9),则将数量为min {Nn,Nm,next-Nf-Nc}的 电 池 投 入 充 电,然 后根据后文提出的电池类型调整策略对电池进行充电调度;若此时满足式(9),则按照基于预测的日内调度策略执行。
2)若此时不满足式(8),则按照基于预测的日内调度策略执行。
2.3.2 电池类型调整策略
判断此时Ncm,next是否为0:若Ncm,next=0,则将投入充电的电池划归为第1 类电池;若Ncm,next>0,则将投入充电的电池划归为第2 类电池,然后,将全部第2 类电池按照SOC 值由大到小进行排列,并从SOC最大的开始,选取等同于投入充电电池数量的电池,将其划归为第1 类电池。
总体调度策略流程如图2 所示。
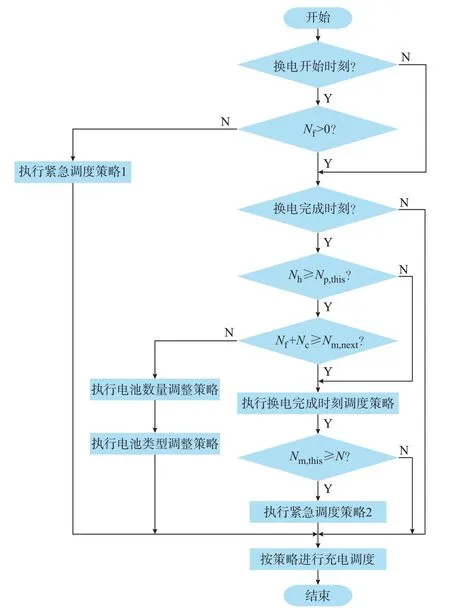
图2 总体调度策略流程图Fig.2 Flow chart of overall scheduling strategy
3 以削峰为目的的时间-功率计算模型
根据换电需求预测与电池调度策略确定允许充电时段后,以实现换电站参与电网削峰为目的,建立电池充电功率和实际开始、结束充电时间计算模型。
3.1 假设条件
1)换电站内电池型号、规格相同;
2)电池采用恒功率进行充电;
3)充电功率允许在一定限度内超出电池的额定充电功率;
4)不考虑站内除充电机以外的其他设备,如换电机器人、监控设备、操作台等产生的负荷;
5)若乏电电池无法在允许充电时间范围内充电至目标电量,则从tzz开始以最大允许充电功率充电至目标电量。
3.2 目标函数
为实现该充电调度策略的削峰效果,以负荷曲线离差平方和最小为目标建立目标函数f[20],即
利用张航等人研究的量子行为粒子群优化(Quantum PSO, QPSO)算法对微型飞行器进行三维路径规划[2],首先将三维坐标数据通过坐标变换和离散有限平面的方法化简为一维数据,然后建立新地图和粒子适应度函数,适应度函数决定了静态和动态壁障的适应值,最后通过QPSO算法获得一条全局最优路径,对UAV+RFID数据模型进行计算可以得到一条S到F点的最优路径,其中L2的长度为88.82。仿真结果如图6所示。
式中:t1、t2分别为换电站开始和结束运行的时刻;PL(t)为t时刻不包括换电站负荷的背景负荷值;Pcz(t)为t时刻换电站总的充电功率;Pc(k)为第k块电池在t时刻的充电功率;Pav为换电站运营时间段的背景负荷均值。
3.3 约束条件
1)充电功率约束。电池充电功率不能超过充电机充电功率的范围:
式中:Pc,min为充电机最小充电功率;Pc为充电机充电功率;Pc,max为充电机最大充电功率。
2)充电时间范围约束。电池实际充电时间应处于由调度策略决定的允许充电时间范围内:
式中:tcstart为电池实际开始充电时间;tcend为电池实际结束充电时间。
3)充电电量约束。保证电池能够充电至目标电量,以满足换电要求:
式中:Snow为电池当前时刻的SOC 值。
4)站内变压器容量约束。换电站充电总负荷不能超过换电站配备的变压器容量上限:
3.4 求解模型
针对本文提出的电池调度策略和目标函数,确定求解过程如下:
1)首先,确定各时段开始时刻矩阵Tsd和本时段已换电次数变量Nh,当时间等于Tsd矩阵的任一值时,Nh归0 并重新开始计数。
2)然后,建立如下大小为1×(N+1)的矩阵:第1 类电池充电状态矩阵BFTB、第2 类电池充电状态矩阵BSTB、当前电池电量矩阵BSnow、目标电池电量矩阵BSmb、允许最早开始充电时间矩阵Btzz、允许最晚完成充电时间矩阵Btzw、充电功率矩阵Bpc、实际开始充电时间矩阵Btcstart、实际结束充电时间矩阵Btcend,矩阵的每个位置固定对应一个充电位。其中,BFTB和BSTB为0-1 矩阵。各矩阵应满足如下约束。
(1)电池状态约束:
式中:BFTB(iB)表示矩阵BFTB中的第iB个元素,以下同理。
(2)充电时间约束。Btzz、Btzw、Btcend、Btcstart应满足以下约束:
(3)电池数量约束:
式中:sum(·)表示对矩阵的所有元素进行求和。
(4)电池电量约束:
(5)充电功率约束:
(6)BSmb、BSnow、Bpc、Btcend以 及Btcstart应 满 足 以 下约束:
3)最后,使用MATLAB 进行电池调度策略的编程,根据输入数据和调度策略,对上述矩阵的对应位置进行赋值。
3.5 求解算法
针对本文提出的调度策略和时间-功率计算模型,使用差分算法进行求解。差分算法的基本思想是利用随机产生的父代种群,由父代种群进行变异、交叉得到子代种群,通过比较二者的适应函数值进行优胜劣汰,得到新一代父代种群,经过迭代计算,得到最优解[21]。
结合前文确定的电池调度策略和目标函数,确定差分算法的求解过程如下。
步骤1:获取换电需求发生时间点数据和从车上换下电池的SOC 数据。
步骤2:将数据输入调度策略程序,得到投入充电电池的允许充电时间范围,并通过前文建立的矩阵对数据进行实时更新和记录。
步骤3:根据步骤2 得到的数据,生成投入充电电池的充电开始时间的父代种群Psc、充电结束时间的父代种群Pec和充电功率的父代种群Ppc。
步骤4:确定变异方式。随机选择3 个不同的父代种群内的个体P(r1)、P(r2)、P(r3),有第j个变异个体M(j)为:
式中:F为变异算子。
对Psc和Pec进行变异,得到二者的变异种群Msc、Mec,并对变异种群进行边界吸收,即超出上限时取上限、低于下限时取下限,再根据Msc、Mec计算出充电功率的变异种群Mpc,得到完整的变异种群。
步骤5:将Psc和Msc、Pec和Mec分别进行交叉操作,即进行两个种群内个体向量部分值的交换,得到交叉种群Csc、Cec,再根据Csc、Cec充电功率的交叉种群Cpc,得到完整的子代种群。
步骤6:将父代种群和子代种群代入目标函数,进行二者同编号个体间的一对一竞争,保留二者中令目标函数取得更小值的个体作为新一代父代种群个体。
步骤7:判断是否满足终止条件,若满足则输出最优结果并停止计算,否则开始下一轮循环。
4 算例分析
4.1 算例数据
本文采用中国某实际电动重卡换电站的有关参数作为算例进行策略验证。该换电站服务的电动重卡群体为50 辆,站内电池与服务的电动重卡均配备相同型号的电池,额定充电功率Pce为240 kW,最大充电功率不能超过额定充电功率的两倍。选择该换电站所在台区的变压器在某一个月内的实测负荷数据,并对数据进行一定平滑处理后作为算例使用的背景负荷数据。
换电站配置参数如下:换电站常用电池数量N为8 个,充电机功率下限Pc,min为0,充电机功率上限Pc,max为480 kW,电池额定容量WB为288 kW·h,司机最长等待时间twait为15 min,站内变压器容量上限PT,max为2 000 kV·A,站内变压器功率因数cosφ为0.9,单次换电时长th为6 min。
根据换电站配置数据及式(1),可得划分时段的步长tp为72 min,按照此步长对一天的数据自00:00开始进行划分,得到换电站历史运行数据部分统计结果如表1 所示。
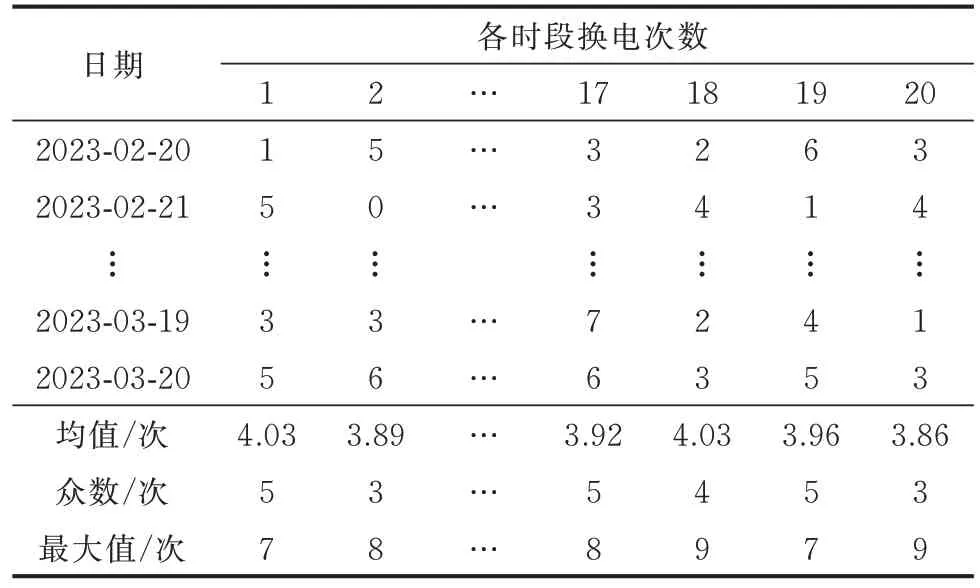
表1 换电站历史换电数据Table 1 Historical battery swapping data of battery swapping station
使用各时段众数作为各时段基本需求预测值Np,next,使用各时段最大值作为各时段极端需求预测值Nm,next。
4.2 策略验证
假定换电站以电池全部满电的状态从17:00 开始执行充电调度策略。确定背景负荷的高峰“峰顶”时段为19:00—20:20。选取某一日17:00—21:00换电站实际历史运行数据作为第1 组换电需求数据。
根据本文提出的时间-功率计算和求解模型,使用差分算法进行求解,得到施加充电调度策略前后的换电站总充电功率,如图3 所示。
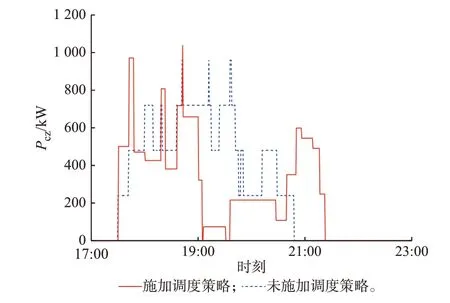
图3 第1 组数据下的换电站总充电功率Fig.3 Total charging power of battery swapping station under the first set of data
由图3 可知,在施加充电调度策略前,换电站在“峰顶”时段有着较高的总充电功率,呈现出“峰上加峰”的现象。而在施加了调度策略之后,换电站的充电负荷得到了明显的前移和后移。这是因为对于在负荷峰顶之前换下的电池,立刻以较大的功率开始充电,尽可能在到达负荷峰顶时段前充满,减少了换电站在负荷峰顶时段的总充电功率。同时,使得站内拥有更多的满电电池,可以在继续进行一定次数的换电服务后,依然满足实时修正策略的约束式(9),减少负荷峰顶时段充电电池数量,进一步削减换电站在负荷峰顶时段的总充电功率,避免了“峰上加峰”现象。
根据实际调研数据,twait的取值范围约为10~20 min。因此,本文对twait取值变化对调度结果带来的影响进行了探究。当twait分别取10、15、20 min 时的调度结果见附录A。由附录A 可知,twait取值的变化对调度结果的影响很小,本文最终选取中间值15 min。
为进一步验证策略和模型的有效性,使用泊松分布,根据表1 中各时段换电次数均值随机生成一组换电需求发生时间点,根据换电站历史数据统计,从车上换下电池的SOC 呈现出近似于正态分布的规律,如图4 所示。
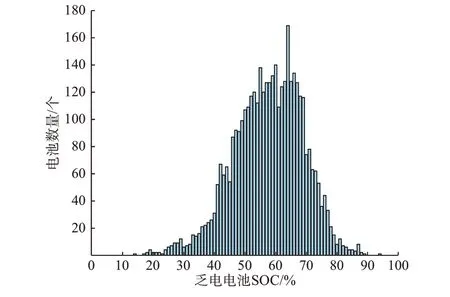
图4 乏电电池SOC 分布Fig.4 SOC distribution of discharged batteries
因此,对应换电需求发生时间点随机生成一组符合正态分布规律的SOC 值,二者结合作为第2 组换电需求模拟数据,其计算结果如图5 所示。可以发现,对于模拟数据,本文提出的调度策略和计算模型也取得了明显的对充电负荷进行前后移动的效果。
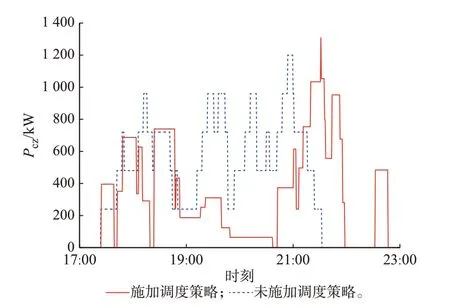
图5 第2 组数据下的换电站总充电功率Fig.5 Total charging power of battery swapping station under the second set of data
通过对比图3、图5 可以发现:
1)对于两组数据的计算结果,充电负荷前移的幅度均明显低于后移的幅度,这是因为本文对于第1 类和第2 类电池的允许充电时长划分是在满足换电需求的基础上,尽可能向后延长允许充电时间。因此,峰顶时段换下的电池的充电时间被明显后移。而少量的负荷前移是因为本文假设电池的充电功率最大不超过额定充电功率的两倍,在以平抑负荷波动为目标函数的计算模型作用下,最先投入充电的电池会以更大的充电功率进行充电,从而更早结束充电过程,减少换电站在负荷峰顶时段的充电负荷。同时,由附录A 的结果对比可知,twait取值的变化对调度结果带来的影响均处于负荷后移的部分,也从侧面印证了调度策略在充电负荷后移中发挥了作用。
2)由图5 可知,在22:00—23:00 出现了未施加调度策略时换电站总充电功率为0,而施加调度策略后有较大充电功率的现象,除上文所介绍的负荷后移的原因之外,还因为在Nf与Nc之和能够满足换电需求时,部分电池在调度策略的控制下不投入充电,直到因换电需求陆续产生,站内Nf与Nc之和不能满足换电需求时,则将未投入充电的电池投入充电,造成了部分充电负荷较大幅度后移的现象。
3)对于两组数据,均不能实现将负荷峰顶时段的换电站充电负荷完全前移或后移,这是因为在调度策略的约束条件式(6)—式(9)下,站内需保有一定数量的满电和充电电池,以满足后续的换电需求。
将换电站数量增加至10 座,假定其配置参数和历史运行数据均相同,采用前文生成模拟数据的方法生成这10 座换电站的换电需求模拟数据,计算结果如图6、图7 所示。由图可知,施加充电调度策略后,10 座换电站在峰顶时段的总充电功率最高点由9 156 kW 下降到3 393 kW,降低了62.94%,在整个峰顶时段的总充电功率降低了43.24%;台区总负荷最高点由82 417 kW 下降到78 241 kW,降低了5.07%,在整个峰顶时段的台区总负荷降低了2.95%。
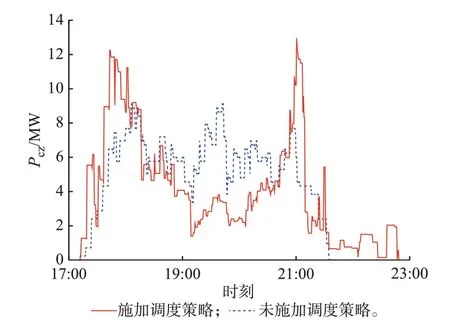
图6 10 座换电站的总充电功率Fig.6 Total charging power of ten battery swapping stations
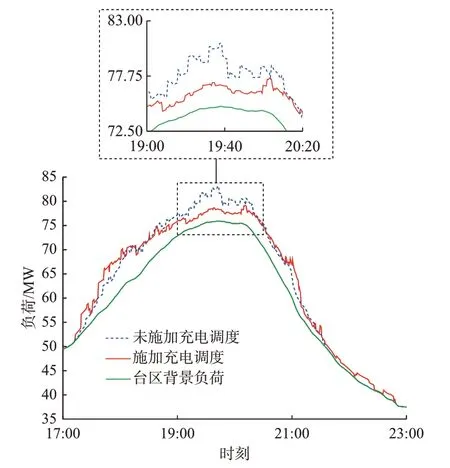
图7 10 座换电站时的台区总负荷Fig.7 Total load of transformer station area with ten battery swapping stations
本文提出的充电调度策略大幅减小了换电站在峰顶时段的总充电功率,且降低了台区总负荷的最大值,实现了参与电网削峰调节。
由于部分充电负荷被移出负荷高峰时段,调度策略能够发挥减少换电站充电成本的效果。换电站充电成本C为:
式中:ct为t时刻的单位电价;Δt为功率采样时间间隔,取36 s。
谷时段(00:00—07:00,23:00—24:00)、平时段(07:00—10:00、15:00—18:00、21:00—23:00)、峰时段(10:00—15:00、18:00—21:00)的分时电价分别为:0.443 0、0.639 7、0.844 4 元/(kW·h)。
由式(25)计算可得,在施加调度策略后,面对17:00—21:00 的换电需求,10 座换电站的充电成本减少了17.9%。
5 结语
本文针对电动重卡换电站的配置和运行情况,提出了换电站需求预测方法。基于预测的日内调度策略和日内实时修正策略,建立了以削峰为目的的时间-功率计算和求解模型,并通过算例分析证明了本文所提策略和模型的有效性。具体结论如下:
1)本文提出的时段划分方式能够配合基于预测的日内调度策略和实时修正策略,确保电池有足够的允许充电时长,实现了灵活的电池充电调度;
2)在满足换电需求的基础上,有效减少了在电网高峰时段的换电站总充电功率,实现了电网削峰;
3)由于充电负荷的移动,在实现削峰的同时还发挥了一定的减少换电站充电成本的作用。
同时,由于本文采用实际电动重卡换电站的配置和运行数据进行分析和计算,所提出的调度策略具有实际应用价值,可以在配置和运行情况与本文算例相似的换电站进行应用推广。然而,在换电站突然面临巨量或极其频繁的换电需求的特殊情况下,本文所提策略的实用性有所降低,且所提算法有待进一步优化,以提升解算速度。
感谢国网商用电动汽车投资有限责任公司在“电网友好型换电站多目标协调互动关键技术研究与示范”项目上为本文研究所提供的数据支持!
附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx),扫英文摘要后二维码可以阅读网络全文。
