限流器配置与网架结构优化协同的受端电网短路电流抑制策略

邓步青，文云峰，于琳琳，蒋小亮

（1.湖南大学电气与信息工程学院，湖南省长沙市 410082；2.国网河南省电力公司经济技术研究院，河南省郑州市 450052；3.国网福建省电力公司经济技术研究院，福建省福州市 350012）

0 引言

近年来，受端电网快速发展，其装机容量和规模不断扩大，加之特高压直流的密集馈入，导致受端电网的网架结构联系更加紧密，其短路电流水平也随之攀升，短路电流超标问题逐年恶化［1］。此外，为保证受端电网对特高压直流的安全接纳，配套交流网架的建设和同步调相机等设备的配置使系统短路电流水平进一步恶化［2］。目前，短路电流超标问题已成为制约受端电网直流承载能力的瓶颈和影响系统安全稳定运行的潜在风险。如何精准有效地抑制短路电流水平已成为受端电网规划和运行中亟待解决的科学问题［3-4］。

就如何有效抑制短路电流超标问题，已有的研究成果主要聚焦于从电网规划和系统运行2 个角度制定相应的规划方案与控制措施［5］。在系统运行层面，通过灵活切换输电线路运行状态以调整系统拓扑结构，在不增加新设备的同时可一定程度控制短路电流水平，但是单一的网架结构优化对短路电流的抑制作用有限，且运行中大规模调整网架结构，可能降低电网运行的可靠性。文献［6］提出了基于自阻抗灵敏度的限制500 kV 主网架短路电流水平的网架调整优化策略，并在广东电网得以应用。但是该方法忽略了网架结构调整对省内潮流的影响和故障后潮流重塑的适应性，且校核过程较为烦琐、时效性较差。文献［7］通过表征线路开断与短路电流约束之间的显式线性关系，提出了计及短路电流约束和N-1 安全约束的短路电流抑制优化模型。文献［8］构建了计及三相短路电流和单相短路电流约束的网架接线调整混合整数非线性优化模型，但是受限于Benders 分解算法对非线性问题处理的局限性，其结果的精确性和算法收敛速度有待提高。

在系统规划方面，可加装限流电抗器和故障限流器（fault current limiter，FCL）等限流设备，弱化系统中电源与负荷的电气联系，从而使短路电流水平满足断路器的开断能力要求，但是降低了系统运行的经济性［9］。以限流电抗器为例，通常装设于短路电流水平超标的线路中，在正常运行时增加了系统无功损耗，线路潮流不再优化，甚至降低了系统稳定性［10］。而故障限流器是一种在正常运行时不会对系统运行造成经济影响，只在故障时才接入的新型限流装置。其中，较为理想的是超导故障限流器（superconducting fault current limiter，SFCL），具有反应速度快、自动触发和自动复位的优势，可在毫秒级的时间内将短路电流限制在合理水平。目前，在中国华东电网的500 kV 网架中，已有SFCL 的示范工程应用实例［11］。文献［12-13］提出了计及暂态稳定性和经济性的SFCL 优化配置模型，并采用非支配排序遗传算法对多目标优化模型进行求解。文献［14］针对直流短路电流超标问题探讨了基于暂态能量流的模块化多电平换流器高压直流电网故障限流器和接地方式的多目标优化模型，实现了对故障限流器配置、接地方式和中线型电抗的多参数综合优化。文献［15］从直流电网双极短路故障后电容放电机理出发，提出了计及故障限流器和直流断路器投切过程的限流电抗器优化配置模型。总体来看，加装故障限流器可以保证网架结构的完整性，但是故障限流器的体积过大且成本较高。

综上所述，为平衡投资成本与短路电流抑制效果，并减少对网架拓扑结构的重塑，本文提出了一种考虑SFCL 配置与网架结构优化协同的短路电流抑制策略。首先，量化和构建了计及SFCL 配置与网架结构优化的短路电流约束。其次，针对多直流馈入和受端电网协调发展的短路电流超标问题，构建了SFCL 配置与网架结构优化协同的多直流馈入受端电网短路电流抑制模型，并基于嵌套Benders 分解算法将主问题分解为多个子问题。最后，采用基于McCormick 包络的交流潮流线性化框架以保证非线性模型的精确近似。通过算例仿真分析，验证所提策略在经济性和短路电流抑制效果方面的有效性和实用性。

1 计及SFCL 配置与网架结构优化的短路电流约束建模

系统正常运行时，SFCL 表现为低阻抗或接近于零阻抗的状态，此时产生的损耗小，在故障发生后，SFCL 快速转换为高阻抗状态，限流电抗串入线路（i，j），此时节点阻抗矩阵发生变化。支路（i，j）串联一个阻抗可等价为支路与等价阻抗并联，即在节点i和j之间追加一个阻抗为Zeq的连支，变换过程如 图1 所 示。图 中:Zi，j为 节 点i、j间 的 互 阻 抗；ZFCL为 故 障 限 流 器 的 阻 抗；Zeq=(-Zi，j)//(Zi，j+ZFCL)=-(Z/ZFCL+Zi，j)。

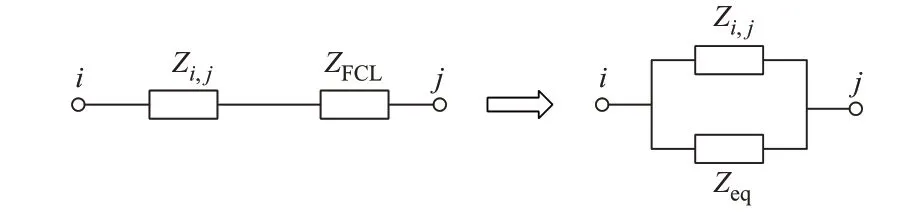
图1 支路等价过程示意图Fig.1 Schematic diagram of branch equivalence process

采用连支法分析SFCL 配置和网络结构拓扑变化对节点阻抗矩阵的影响，即对于p阶交流系统阻抗矩阵Z，在节点i和j之间追加一个阻抗为Zeq的连支后，节点阻抗矩阵Z转变为Z′，任意元素Zk，m的值变为，其计算公式可归纳为式（1）［16］。

式 中:Zk，i、Zk，j、Zi，m、Zj，m为 各 节 点 间 的 互 阻 抗，Zi，i、Zj，j为节点自阻抗，均为阻抗矩阵Z中的元素。

当计及线路和SFCL 待选状态时，需引入0-1 整数变量φl和ψm分别表征线路l和第m个SFCL 是否投建。同时，考虑采用输电网结构优化调节自阻抗值，进而抑制节点短路电流水平。因此，计及SFCL优化配置与网架结构优化协同的自阻抗变化量ΔZ为［17］:

式中:下标p、q表示任意节点；上标“（0）”表示相关阻抗矩阵元素的初始值；ΔZp，q，l和ΔZeq，m分别为输电网结构优化后和SFCL 配置后的自阻抗变化量；φl和ψm分别为表征线路和SFCL 投建状态的0-1 整数变量，取值为1 则表示投建，取值为0 则表示不投建；σl为表征线路结构是否优化的0-1 整数变量，取值为1 表示主动断开，取值为0 则表示不断开；K+l和M分别为待选线路和待选SFCL 的集合；Kl为已建成线路的集合。值得注意的是，对于式（2）中出现的非线性项φlσl，可通过“大M 法”实现线性化。

需要注意的是，本文仅考虑三相短路这一最严重的短路故障类型。规划方案中短路电流需要满足≈1/Zi，i≤的 要 求，即 相 应Zi，i≥1/，其中，IˉSCn表示节点n所允许的最大短路电流。基于上述分析，计及SFCL 优化配置与输电网结构优化的新节点自阻抗Z可表示为:

式中:φy，l为表征第y个规划阶段线路投建决策的0-1 整数变量，取值为1 表示新线路投建，取值为0 则表示不投建；σy，l为表征第y个规划阶段线路结构是否优化的0-1 整数变量，若线路主动断开则取值为1，否 则 取 值 为0；Ai，l和Ai，m均 为 常 数，其 计 算 方 法分别如式（4）和式（5）所示。

2 SFCL 配置与网架结构优化协同的短路电流抑制模型

本文提出的考虑输电网结构优化与SFCL 配置协调的多阶段短路电流抑制模型中，第1 阶段主问题（MP）为规划决策模型，主要确定输电网拓扑优化方案和SFCL 配置方案，第2 阶段子问题（SP）为计及短路电流约束的安全运行校验模型。

2.1 主问题模型

主问题模型以网架结构优化成本和SFCL 配置成本最小为目标函数，即

式中:fMP为主问题目标函数的值；Y为规划阶段集合；K和Ey，l分 别 为 第y个 规 划 阶 段 新 建 待 选 线 路集合和开断待选线路集合；CIN、C、C、C和C分别为总投资成本、新建线路投资成本、线路开断成本、SFCL 安装成本和投资成本；λ为投资折现率；ρy，l为表征第y个规划阶段线路开断状态的0-1 整数变量，取值为1 表示线路处于断开状态，可由线路主动断开或线路未投建2 种情况造成，取值为0 则表示线路处于闭合状态，未进行断开操作；ψy，m为表征第y个规划阶段SFCL 投建决策的0-1 整数变量，取值为1 表示SFCL 投建，取值为0 则表示不投建；为限流容量，即为SFCL 的限流阻抗值大小。

式（6）等号右边第1 项为新线路投建的成本，第2 项为线路的开断成本，第3 项为SFCL 安装的固定成本，第4 项为SFCL 的电阻成本。

模型约束条件如下。

1）投建逻辑约束

对于端点相同的输电线路，需满足序列建设回路约束，SFCL 的配置逻辑亦是如此。由于每条线路走廊所允许建设的线路是有限的，新建线路总量受限，且为保证系统安全稳定运行，在输电网结构优化中，开断的线路数不超过允许的最大值。具体约束如下:

式中:L和L分别为线路和SFCL 的最大投建数量。

2）网架结构优化约束

对于候选新建线路，若线路未投建，则一直处于断开状态；相反，若线路已投建，则可以处于闭合或断开状态。为此，网架结构优化需要满足以下约束:

式中:L为最大主动断开线路数量；R和R分别为SFCL 限流容量的下限值和上限值。

2.2 子问题模型

子问题以运行维护成本最小为目标函数，即

式中:T为时段集合；G为同步发电机集合；C为第i个 火 电 机 组 的 运 行 维 护 费 用；P为 第y个 规 划阶段t时段下第i个火电机组的有功出力。

模型约束条件如下。

1）功率平衡约束

式中:Ky，l为第y个规划阶段已建成线路的集合；S为 已 安 装 的 同 步 调 相 机 集 合；Q为 第y个 规 划 阶段t时 段 下 第i个 火 电 机 组 的 无 功 出 力；P和Q分 别 为 新 能 源 场 站 的 有 功 出 力 和 无 功 出 力；P和分 别 为 第y个 规 划 阶 段t时 段 下 第i条 特 高 压 直流 线 路 的 有 功 功 率 和 无 功 功 率；P和Q分 别 为第y个规划阶段t时段下第i个节点有功负荷需求和无功负荷需求；Gi和Bi分别为第i个节点并联电导和 电 纳；P和Q分 别 为 第y个 规 划 阶 段t时 段下流过交流线路（i，j）的有功功率和无功功率，计算方法分别如式（15）和式（16）所示，且交流线路传输视在功率满足约束式（17）。

式中:Gij和Bij分别为线路（i，j）的电导和电纳；Smaxl为线路l所允许的最大视在功率。

αy，t，i、βy，t，i，j和γy，t，i，j为 便 于 交 流 潮 流 模 型 线 性 化所引入的等效变量，其表达式［18］如下:

式 中:Vy，t，i和θy，t，i分 别 为 第y个 规 划 阶 段t时 段 下 第i个节点的电压幅值和相角。

易知，等效变量之间存在一定的数学关系及性质，并满足一定的限制约束，具体如式（21）—式（24）所示。

式中:Vmin和Vmax分别为最小和最大节点电压限值；θmin和θmax分别为最小和最大相角。

约束式（21）为等效变量αy，t，i的上下限约束；约束式（22）和式（23）可以从式（20）推导得到；约束式（24）反映 了等效变量βy，t，j，i和γy，t，j，i的自对称性 和反对称性。

2）机组出力约束

式中:P和P分别为第i个火电机组的最小和最大技术出力；Q和Q分别为第i个火电机组（或同步调相机）的最小和最大无功出力。

3）直流线路传输功率约束

式中:P和P分别为第i条直流线路所允许的最小和最大传输功率；ξ为直流线路有功功率与无功功率之间的耦合系数，取值为0.5；H为特高压直流线路集合。

4）系统备用容量约束

式 中:R和R分 别 为 系 统 在 第y个 规 划 阶 段t时段的上调和下调备用总需求。

5）系统无功裕度约束

系统仍需要保证一定的动态无功裕度，以保证具备应对无功功率波动的能力，以及避免系统因无功功率不足导致的一系列暂态电压问题和直流换相失败故障。具体约束如下:

式中:MTF为无功功率的转移因子；Q为第y个阶段t时段的系统动态无功需求。

6）短路电流约束

通过SFCL 配置和网架结构优化保证系统所有节点的短路电流水平均在合理范围内，具体约束如下:

式 中:Z为 第y个 规 划 阶 段 自 阻 抗 的 初 始 值；为系统所允许的最大短路电流；B为交流节点的集合。

3 基于Benders 分解的短路电流抑制模型求解算法

针对上述SFCL 配置与网架结构优化协同的受端电网短路电流抑制模型，采用Benders 分解算法进行求解［19］。由于子问题中采用交流潮流模型式（13）和 式（14），为 使 模 型 线 性 化，引 入 了 包 含McCormick 包络的交流潮流线性化处理方法。进一步，为保证潮流线性化精度和收敛精度，引入新的松弛变量将子问题再处理，并构建基于Benders 分解的迭代求解算法，如图2 所示。图中:ε为收敛阈值。

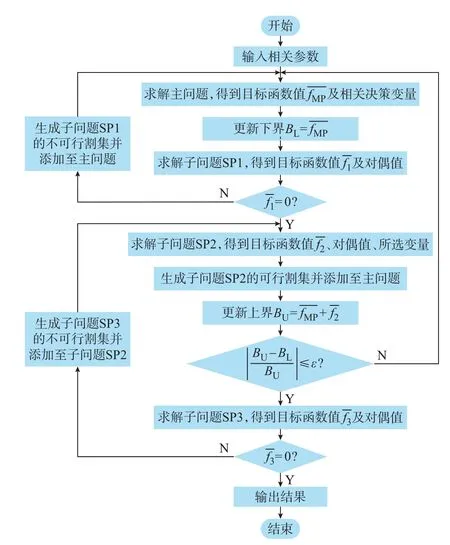
图2 基于Benders 分解的求解算法流程图Fig.2 Flow chart of solution algorithm based on Benders decomposition

求解过程中，主问题保持不变，为输电网结构优化和SFCL 配置的混合整数线性规划（mixedinteger linear programming，MILP）问题；子问题SP1则是保证主问题决策方案的可行性；根据可行的投资决策求解子问题SP2，以获得最小的运行维护成本；子问题SP3 最小化交流潮流松弛误差，保证潮流线性化精度。子问题SP1 至SP3 的具体模型如下。

1）子问题SP1:确保决策方案的可行性。子问题SP1 的目标函数如下:

约束条件如式（15）—式（33）以及式（35）—式（37）所示。

式中:顶标“- ”表示主问题所求解得到的对应变量的值，下同；为子问题SP1 中的相应对偶变量为有 功功率平衡约束（式（36））中 引 入 的 非 负 松 弛 变 量；为 无 功 功 率 平 衡约束（式（37））中引入的非负松弛变量。

由于约束式（17）和式（23）中存在二次项和双线性项，子问题SP1 模型为非线性规划（non-linear programming，NLP）问题。采用McCormick 方法对约束式（17）和式（23）进行松弛处理［16］:

式中:MCC(x1，x2)≈x1x2表示McCormick 松弛。

因此，子问题 SP1 的线性规划（linear programming，LP）形式为:

2）子问题SP2:最小化火电机组的运行维护成本。

子问题SP2 的目标函数如下:

约束条件如式（13）—式（16）、式（21）、式（22）、式（24）—式（33）、式（38）、式（39）以及式（42）所示。

3）子问题SP3:以子问题SP3 松弛误差最小为目标，其中，运行状态变量固定为从子问题SP2 所获取的值。

SP3 的目标函数如下:

约束条件如下:

4）可行性割集和不可行性割集的生成。

式（47）和式（48）所示可行性割集η保证主问题的解转向上界，使Benders 算法收敛。同时，式（49）和式（50）所示不可行性割集也会在迭代中影响最终的方案。收敛后，式（49）所示割集强制=0，从而使式（36）和式（37）中的不平衡功率为0。最后，式（50）所示割集确保=0，这意味着线性化（McCormick 松弛）误差为零。值得注意的是，由于式（50）所示的子问题SP3 的割集是根据子问题SP2的 等 效 变 量（αy，t，i，βy，t，i，j，γy，t，i，j）构 造 的，故 式（50）所示割集在下一次迭代中应该被添加至子问题SP2，而不是主问题。

4 算例分析

为了验证所提出的输电网结构优化与SFCL 配置协同的短路电流抑制模型的有效性，选取改进的IEEE 39 节点系统和河南电网2025—2035 年网架规划数据进行仿真计算。算例中的直流输电均为常规高压直流输电（LCC-HVDC）形式。假设SFCL 的安装成本为250 万元/台，单位电阻成本为150 万元/Ω，而交流线路的投建成本为100 万元/公里，开断成本为100 万元/条。所采用的仿真平台为Intel Core i7-4700MQ4 CPU（2.4 GHz）和8 GB RAM 的个人计算机，编程环境为GAMS 23.7，并采用商用求解器CPLEX 12.6 进行求解。Benders 分解算法的收敛阈值设定为0.000 1。最后，假定各节点具有相同的短路电流限值。为进一步验证本文所提出的SFCL 配置与输电网结构优化协同的短路电流抑制方案的优越性，采用2 个单一抑制措施下的方案进行对比，具体如下:

模型1:仅考虑SFCL 优化配置的短路电流抑制方案；

模型2:仅考虑输电网结构优化的短路电流抑制方案；

模型3:本文所提出的SFCL 配置与输电网结构优化协同的短路电流抑制方案。

根据叠加定理，可定义电力系统中任意2 个节点i、j之 间 的 等 值 阻 抗Zi，j，equ为2 个 点 之 间 的 电 气距离［20］:

同时，为更好地表征短路电流的抑制效果，定义平均绝对百分比误差（MAPE）指标:

4.1 改进的IEEE 39 节点测试系统算例

改进的IEEE 39 节点测试系统包含39 个节点和46 条线路，如图3 所示。假设各节点的短路电流限值为14 kA。对于第1 个规划阶段，在节点30 和8分别接入额定容量为200 MW 的新能源发电机组W1/PV1 和W2/PV2，其中，W 表示风电场，PV 表示光伏电站。此外，一条额定容量为600 MW 的直流线路h1 从节点18 接入。对于第2 个规划阶段，在节点38、34 和35 分别接入额定容量为400 MW 的新能源发电机组W3/PV3、W4/PV4、W5/PV5，额定容量为600 MW 的直流线路h2 和h3 从节点21 和19接入。另外，为体现规划需求，负荷在标准系统上扩大1.4 倍。第1 个规划阶段短路电流超标的问题节点为3，第2 个规划阶段短路电流超标的问题节点为3、26、17。

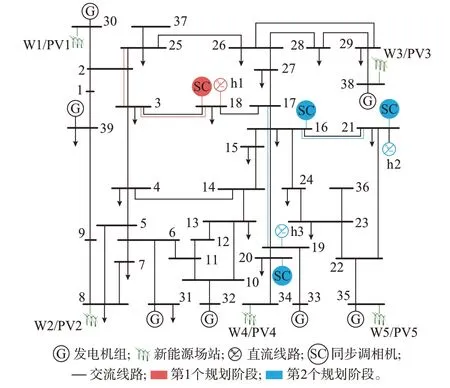
图3 改进的IEEE 39 节点测试系统Fig.3 Modified IEEE 39-bus test system

表1 详细给出了3 个模型下的短路电流抑制方案。表中:R表示故障限流器的阻抗。在短路电流抑制效果方面，3 种方案下均未发生短路电流超标，都具有较好的抑制效果。具体而言，模型3 所得到的短路电流协同抑制方案的短路电流改善效果最为明显，短路电流平均下降率为20.28%，较单一的SFCL 配置方案和输电网结构优化方案高2.74%和4.67%。从经济性角度来看，3 个对比模型中投资成本由高到低分别为模型2、模型1 和模型3，具体分别为0.306 5亿元、0.279 8亿元和0.233 2亿元；在运行成本方面，模型1的运行成本最高，为8.821 8亿元，较模型2和模型3分别高出0.217 1亿元和0.175 4亿元。这是因为加装SFCL 会在一定程度上增加系统的网损，导致系统运行成本增加，由于模型1 仅仅依靠SFCL 配置来降低短路电流，也导致了SFCL 的配置总量最大，从而导致模型1 的运行成本最高。对于模型2 所得到的短路电流抑制方案而言，输电网结构改变较大，开断线路过多，对于直流闭锁故障等会带来严重的故障后潮流重塑而言，重要断面的潮流承受能力存在潜在风险。总之，SFCL 配置与输电网结构优化协同可以兼具经济性和短路电流抑制效果。在计算效率方面，模型3 的总耗时为96.72 s，其中，主问题、子问题SP1、子问题SP2 和子问题SP3的执行时间分别为8.34、21.71、40.56、26.1 s，规划问题计算时效在可以接受的合理范围内。

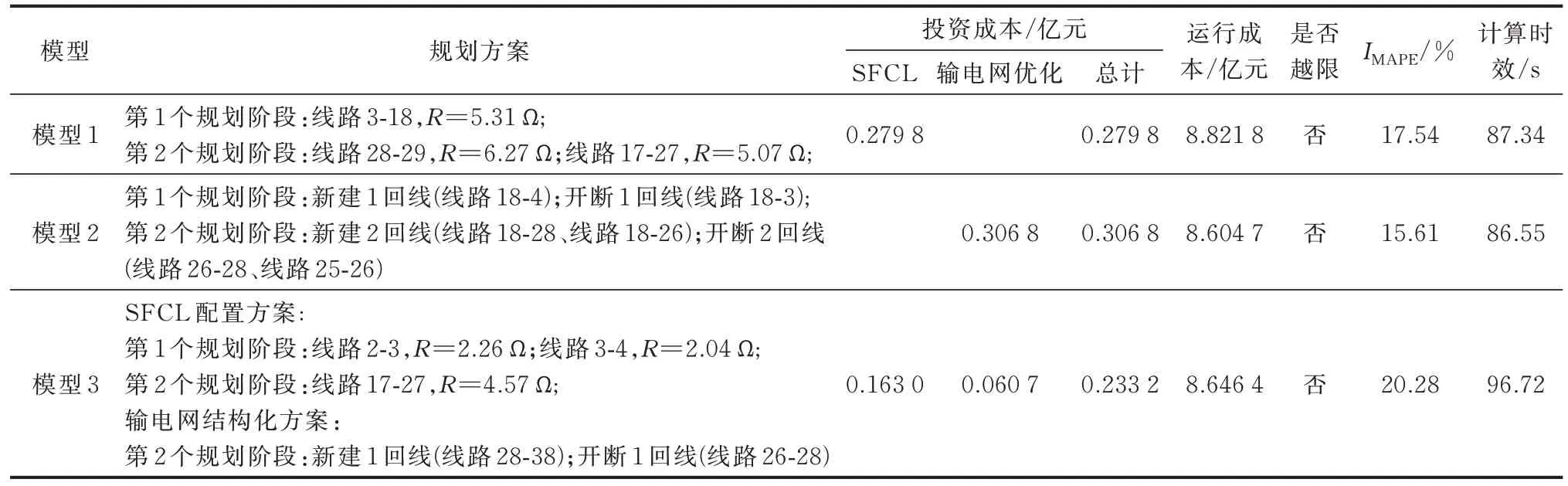
表1 改进的IEEE 39 节点测试系统短路电流抑制方案Table 1 Short-circuit current suppression scheme of modified IEEE 39-bus test system

短路电流抑制方案实施前后的系统短路水平如图4 所示。由图4 可知，采用本文所提出的输电网结构优化与SFCL 配置协同的短路电流抑制策略，能有效且针对性地降低短路电流越限节点的短路电流水平，且不会导致其他非越限节点的短路电流升高或升高过多，这说明了本文所提出的短路电流抑制策略的有效性。

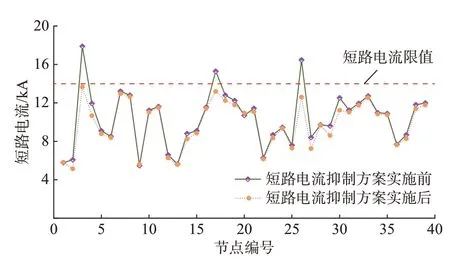
图4 改进的IEEE 39 节点系统的短路电流水平Fig.4 Short-circuit current level of modified IEEE 39-bus system

表2 详细展示了在协同抑制规划方案实施前后短路电流越限节点与各发电机节点之间的电气距离。需要注意的是，由于同步调相机、新能源和直流均会提供短路电流，将直流馈入点和接有同步调相机、新能源的节点作为发电机节点考虑。从表2 可以看出，节点3、17 和26 与各发电机节点之间的电气距离均相对较小，当这些节点发生短路时，各发电机节点均会产生较大的短路电流并汇集至这些节点，故这些节点的短路电流很大。而通过SFCL 配置与输电网结构优化的协同方案，则能增大节点与各发电机节点之间的电气距离，弱化其电气联系，进而将其短路电流水平限制在合理范围内。以节点3为例，其与系统中各节点联系紧密，属于系统中最重要的节点之一，通过在线路3-4 和2-3 上配置SFCL，则有利于在节点3 发生短路故障时，削弱节点3 与其他节点的电气联系，从而有效降低节点3 的短路电流水平。

由图2 可知，子问题SP3 通过子问题SP3 和SP2 之间的循环在迭代求解过程中最小化松弛误差，其松弛误差结果如图5 所示。可以看出，经过5 次迭代后系统的松弛误差为0，意味着线性化模型的解与原混合整数非线性规划（MINLP）问题的解一致。作为对比，在GAMS 中直接调用求解器对原问题进行求解，最终未得到可行的短路电流抑制方案。这也说明根据图2 所示的Benders 求解框架将原MINLP 问题分解为多个子问题，增强了问题的可处理性。

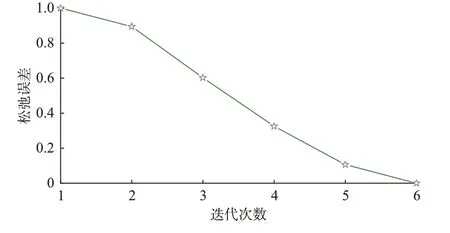
图5 松弛误差Fig.5 Relaxation error

4.2 河南电网规划系统算例

根据河南电网实际运行情况，以短路电流耐受水平值63 kA 为参照，利用BPA 软件对附录A 图A1所示的河南电网2025—2035 年网架规划方案进行短路电流水平测试，发现在2025 年规划方案下，邵陵和中州节点存在短路电流超标现象；2030 年规划方案中新增节点惠济、郑州；2035 年规划方案中新增节点洹安和武周。为进一步证明本文所提出的短路电流抑制策略的有效性和可扩展性，以图A1 所示的河南电网2025—2035 年规划方案下电源、网架和负荷数据为基础进行测试［21］。与改进的IEEE 39节点系统算例类似，对比了3 种模型下的短路电流抑制方案，具体如表3 所示。

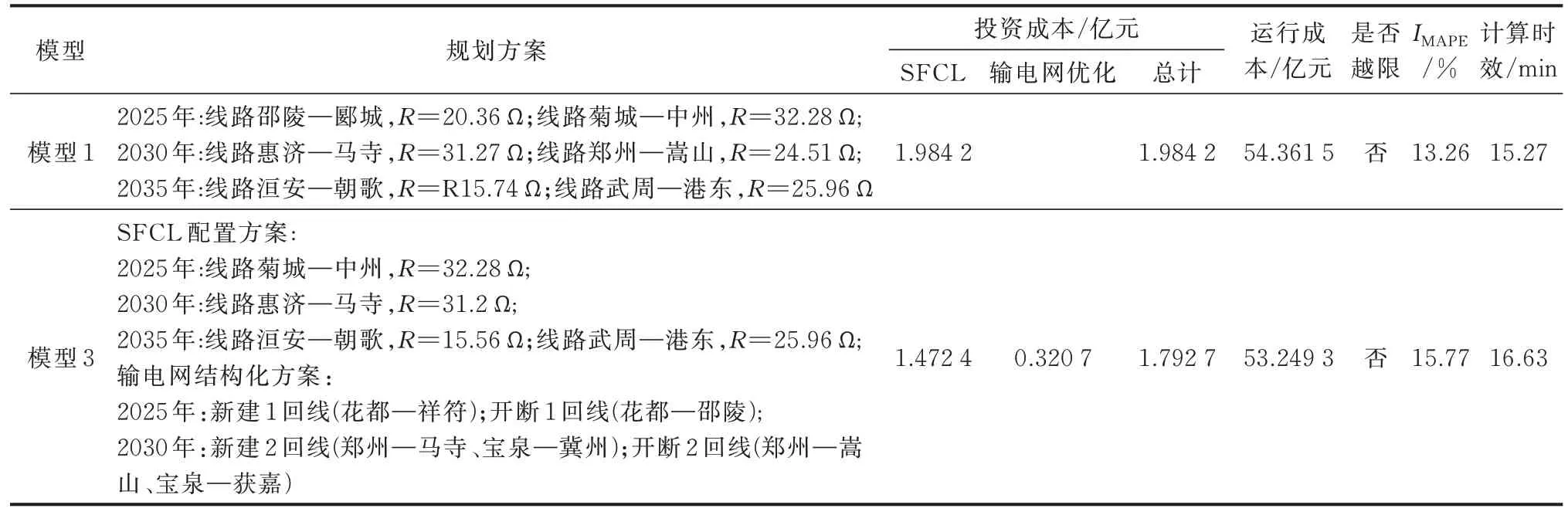
表3 河南电网2025—2035 年短路电流抑制方案对比Table 3 Comparison of short-circuit current suppression scheme of Henan power grid of China in years 2025 to 2035

总体来看，模型1 和模型3 都表现出较为不错的短路电流抑制效果。但相较于模型1，通过SFCL 配置与输电网结构优化的协同，模型3 以更优的经济性达到了更佳的短路短路电流抑制效果。模型3 与模型1 方案的主要差别在于，对于2025 年邵陵节点的短路电流超标问题，主要采取断开线路花都—邵陵，并在线路花都—祥符之间新建一回线路；针对2030 年郑州节点的短路电流越限问题，采取将郑州—嵩山1 回线改接至马寺，同时宝泉改接冀州节点。对于2035 年，2 种方案下均通过配置SFCL 的方式抑制短路电流，究其原因，主要是河南电网到2035 年后电源侧和负荷均基本达到饱和，网架结构稳定，不宜对网架拓扑进行调整，这也符合电网规划工作的准则。在算法的时效性方面，河南电网2035年规划网架下的计算耗时为16.63 min，其中，主问题、子问题SP1、子问题SP2 和子问题SP3 的执行时间分别为1.42、3.68、7.89、3.64 min。对比表2 和表3可以看出，随着系统规模的增大，本文所提模型的计算耗时大幅提高，显著影响其计算效率。同时，对比附录A 图A2 和图5 可以看出，虽然河南电网2035年规划网架规模远大于IEEE 39 节点系统，但依旧保持良好的收敛性，在7 次内收敛。

值得注意的是，模型2 仅考虑通过输电网结构优化，该模型不存在可行方案。这是由于电气联系更为紧密的多直流馈入受端电网对直流落点近区的配套交流网架要求较高，需要保证具有充足的交流通道以保证直流功率的馈出，大规模的网架拓扑调整无法满足系统的潮流传输需求。

附录A 图A3 对比了短路电流抑制策略实施前后2035 年河南规划电网短路电流水平的对比结果，进一步证明了本文所提出的短路电流协同抑制策略对于实际电网的适用性。

5 结语

本文针对受端电网局部短路电流水平超标的问题，提出了一种考虑SFCL 配置与网架结构优化协同的短路电流抑制策略。首先，量化和构建了计及SFCL 配置与网架结构优化的短路电流约束。其次，构建了SFCL 配置与网架结构优化协同的多直流馈入受端电网短路电流抑制模型，引入了包含McCormick 包络的交流潮流线性化处理方法，并构建基于Benders 分解的迭代求解框架以保证问题的收敛精度。最后，在改进的IEEE 39 节点测试系统上和河南电网2025—2035 年规划方案上进行验证，得到以下结论:

1）对于电气联系更为紧密的实际电网，单一的网架结构优化已无法解决短路电流超标问题，而SFCL 配置的经济成本太高。相较于单一措施下的短路电流抑制方法，所提出的短路电流协同抑制策略更具适用性，能在兼顾经济性的同时达到更好的短路电流抑制效果。

2）所提出的基于Benders 分解的迭代求解框架提高了问题的可解性，保证了问题的收敛精度。

本文深入研究了计及SFCL 与网架结构优化协同的短路电流抑制措施，下一步的研究工作将在模型中进一步考虑暂态稳定和源荷不确定性，并研究模型在送端电网的适应性。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。