面向光伏集群的配电网模型-数据联合驱动无功/电压控制

路小俊，吴在军，李培帅，沈嘉伟，胡敏强

（1.东南大学电气工程学院，江苏省南京市 210000；

2.南瑞集团有限公司（国网电力科学研究院有限公司），江苏省南京市 211106；3.南京理工大学自动化学院，江苏省南京市 210094）

0 引言

在中国“碳达峰·碳中和”目标的背景下，光伏（photovoltaic，PV）装机容量迅速增加，配电网是分布式光伏（distributed photovoltaic，DPV）消纳的重要载体，DPV 的高比例接入引发了网损增加、电能质量恶化等一系列问题［1］。无功/电压控制（volt/var control，VVC）可以有效降低系统的网损、改善电压分布，对于促进DPV 的安全经济并网具有重要作用［2］。

DPV 规模化、多点分散接入的发展趋势极大地增加了配电网的复杂性和管控难度，基于集群划分的分布式VVC 能够实现群间的协同与群内灵活自治，是应对该问题的有效解决方案［3］。文献［4］设计了适应于DPV 集群化并网的体系架构；文献［5］基于社团理论提出了一种虚拟集群动态划分方法；文献［6］考虑功率平衡度和节点耦合度，在集群划分的基础上建立了先有功后无功的电压调控策略；文献［7］提出了基于PV 集群贡献度的配电网VVC 策略。上述研究侧重于DPV 集群控制的架构以及集群划分方法，分析了集群控制的优势以及有效性，但是对于如何实现群间的协同并未进行深入的探索。

在基于集群划分的分布式控制框架中，群间协同下的决策应具备良好的全局趋优性，分布式算法是保证决策全局趋优能力的关键［8］，其中，交替方向乘子法（alternating direction method of multipliers，ADMM）是当前分布式算法的典型代表。文献［9］提出了集合分布式优化与本地控制的双层电压控制策略，利用ADMM 进行了多个集群协同优化模型求解，有效实现了群间协同。文献［10-11］建立了配电网的分布式VVC 模型，并通过ADMM 实现模型的可靠求解。文献［12］分析了ADMM 收敛速度偏慢的问题，并提出了加速ADMM 的算法。虽然ADMM 具有较好的收敛特性，可以实线非光滑函数的优化，但是其存在收敛速度偏慢的问题，制约了其在分布式优化中的应用。随着DPV 接入比例的提高，模型求解的难度进一步提高，对算法收敛性提出了更高的要求。

DPV 出力不确定性特征显著，其短时波动会导致配电网实时运行工况扰动，本地控制成为当前集群自治的重要手段［13］。文献［14-15］提出了基于DPV 的本地控制策略，以实时应对配电网电压越限和快速波动的问题。本地控制虽然可以根据实时运行工况扰动快速响应，但是其不具备全局趋优的能力。近年来，迅速发展的数据驱动技术为配电网的实时优化控制提供了新的思路和可能性［16-17］。文献［18］基于深度强化学习（deep reinforcement learning，DRL）提出了配电网在线无功优化策略，根据配电网运行状态实时调整无功设备动作决策。文献［19］基于多智能体深度强化学习（multi-agent deep reinforcement learning，MADRL）框架，提出了数据驱动的分布式VVC 策略，保证了决策的全局趋优性。文献［20］提出了包含小时级调度以及分钟级调度的配电网多时间尺度无功优化策略，第1 阶段和第2 阶段分别采用了集中式优化和DRL 策略，具有重要的借鉴意义，但是其集中式优化对于多个PV 集群复杂模型的求解具有一定的局限性。

基于上述背景，本文结合分布式优化与DRL 的优势，提出了面向PV 集群的模型-数据联合驱动VVC 策略，构建了以有载调压变压器（on-load tap changer，OLTC）、并联电容器（capacitor bank，CB）和DPV 逆变器为调控设备的日前VVC 模型，并提出 Nesterov 加 速 梯 度 的 ADMM（Nesterov accelerated gradient ADMM，N-ADMM）；利用部分可观马尔可夫博弈（partially observable Markov game，POMG）对DPV 集群实时VVC 模型进行表征，提出基于迭代终止惩罚函数的改进多智能体深度确定性策略梯度（multi-agent deep deterministic policy gradient，MADDPG）算法，对训练流程进行了改进，提高了训练效率。

1 分布式两阶段VVC 框架

基于DPV 集群的划分，考虑群间协调与群内自治，将全局优化控制与本地实时控制相结合，提出一种面向PV 集群的配电网模型-数据联合驱动VVC策略。该策略下的日前-日内两阶段VVC 框架如图1 所示。该框架下，各PV 集群具有相对独立的控制中心。将控制中心拟合成进行决策制定的智能体，基于配电网的运行目标，考虑网络参数、调控资源、PV 功率、负荷数据等信息。各智能体群内自治，同时相邻的智能体进行信息交互，实现群间协同。各智能体内嵌模型-数据联合驱动的VVC 策略，并对日前与日内实时VVC 决策进行协调优化。

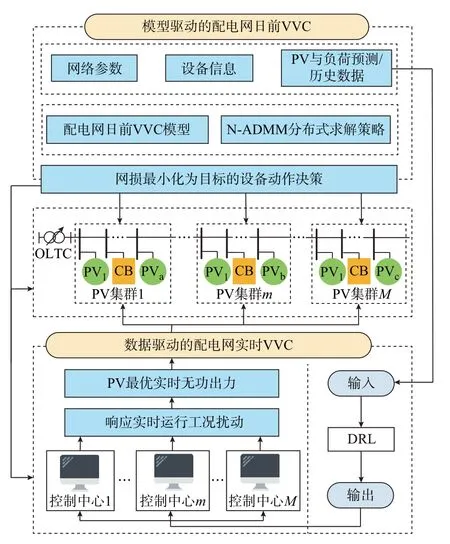
图1 分布式两阶段VVC 框架Fig.1 Framework of distributed two-stage VVC

在日前VVC 阶段，利用模型驱动对OLTC、CB等离散设备的挡位和PV 无功出力决策进行动态优化，提高系统运行的安全性。该阶段不需要对实时运行工况进行快速响应，充分发挥了模型驱动的可靠性和全局最优性。考虑到离散设备的使用寿命，该阶段设置了OLTC 和CB 动作次数限制。此外，该阶段的动作决策将为日内实时VVC 环节提供必要的输入参数。

在配电网实时VVC 阶段，各智能体根据配电网的日内实时运行工况，自适应给出PV 的无功出力优化决策。该环节的实现依赖于DRL 的策略框架，各智能体根据配电网的运行目标，利用MADDPG算法进行离线训练。训练完成的智能体根据实时观测量结果（如PV 实时有功功率、实时负荷、实时电压波动等），在毫秒级的时间尺度上给出在线控制策略［21］，从而保证了VVC 策略对于配电网运行工况的扰动快速响应能力。

2 分布式两阶段VVC 模型

2.1 配电网日前VVC 模型

配电网日前VVC 环节考虑多个PV 集群间的协同调度，基于分布式框架实现系统运行的全局优化，其运行目标函数为:

式中:c为集群编号；G为所有集群的集合；t为调度时刻；T为调度周期内所有调度时间的集合；Ec为集群c内部所有支路的集合；Φc，t，loss为集群c在t时刻的网 损；ij为 从 节 点i到 节 点j的 支 路；lij，t为t时 刻 支 路ij上电流的平方；rij为支路ij上的电阻。

本文利用Dist-flow 模型并结合二阶锥松弛来构建配电网潮流模型，该模型的凸特性可以保证其求解的高效。式（2）、式（3）分别为有功、无功功率平衡约束；式（4）为节点电压平衡约束；式（5）为二阶锥松弛约束，其将原始的非凸二次约束松弛为凸的二阶锥约束，保证了模型的可解性；式（6）为节点电压约束。

式 中:Pij，t、Qij，t分 别 为t时 刻 支 路ij上 的 有 功、无 功 功率；pj，t，PV和pj，t，PD分 别 为t时 刻 节 点j上PV 机 组 的 注入 有 功 功 率、负 荷 的 有 功 需 求；qj，t，CB为t时 刻 节 点j上CB 的 注 入 无 功 功 率；qj，t，PV、qj，t，QD分 别 为t时 刻 节点j上PV 机组的注入无功功率、负荷的无功需求；vi，t、vj，t分 别 为t时 刻 节 点i、节 点j上 电 压 的 平 方；εij为 支 路ij的 电 抗；Vi，t，min、Vi，t，max分 别 为 节 点i在 调 度t时刻的电压下限、上限；Nc为集群c内部所有节点的集合。

在配电网VVC 模型中，PV 逆变器向系统提供有功和无功支撑，其运行约束如下所示:

式 中:Nc，PV为 集 群c内 部 具 有PV 的 节 点 集 合；si，t，PV为t时刻节点i上PV 机组的容量。

离散设备OLTC 和CB 的运行约束如下:

式 中:Nc，CB为 集 群c内 装 设 有CB 的 节 点 集 合，vbase，t为 一 次 侧OLTC 电 压 幅 值 的 平 方；v1，t为OLTC 二次侧电压幅值的平方；rmin为OLTC 最小变比的平方；ξs为OLTC 的两个挡位之间变比平方的差值，即调节步长；σs，t，OLTC、σi，s，t，CB分别为OLTC、CB 的挡位s的调节变量；qtap为CB 机组的一个挡位的无功出力；Tmax，OLTC、Ti，CB，max分 别 为OLTC、CB 的 最 大 挡 位；σm-1，t，OLTC为t时 刻OLTC 在m-1 挡 位 的 调 节 变量；σi，m，t，CB为t时 刻 节 点i上CB 在m挡 位 的 调 节 变量。σs，t，OLTC和σi，s，t，CB均 为 二 进 制 变 量，当 所 有 挡 位的调节变量全为0 时，表示处于最小挡位；全为1 时，表示处于最大挡位。式（8）—式（10）为OTLC 运行约束，式（11）—式（13）为CB 运行约束。

OLTC 和CB 的使用寿命受动作次数影响较大。在调度周期内对其动作次数进行限制。式（14）、式（15）和式（18）、式（19）分别为前后两个时刻OLTC 和CB 动作挡位限制，式（16）、式（17）和式（20）、式（21）分别为OLTC、CB 调度周期内最大动作次数限制。

式中:δt，OLTC，IN、δt，OLTC，DE分别为当前时段、前一时段OLTC 的挡位变化状态，均为二进制变量；δi，t，CB，IN、δi，t，CB，DE分别为当前时段、前一时段CB 的挡位 变 化 状 态，均 为 二 进 制 变 量；NOLTC，max、Ni，CB，max分别为OLTC、CB 在一个调度周期内挡位的最大调节次数。

上述模型针对单一PV 集群，多个PV 集群则通过群间信息交互实现协同。多个集群间的交互信息以边界条件为载体，本文采用了文献［10］中的边界条件构建方法，边界条件约束如式（22）所示。

式中:Gc为与集群c直接相邻的集群集合；bc，t(n)为集群c的边界条件；bn，t(c)表示集群n的边界条件。当两个相邻集群相对应的边界条件一致时，信息交互完成。

2.2 基于POMG 的配电网实时VVC 模型

基于OLTC 和CB 的小时级设备动作决策，在配电网的实时VVC 环节，利用MADRL 对PV 集群进行控制。本文同时考虑降低系统网损以及避免电压越限的问题，构建了配电网实时多目标VVC 模型。同时，考虑到系统网损与电压的量纲不一致的问题，采用了文献［22］的规范化处理方法，将网损与电压均转化为无量纲属性。PV 集群c的实时多目标VVC 数学模型如下所示:

式 中:Φc，t，viol为t时 刻 系 统 节 点 电 压 越 限 偏 差 的 和；分 别 为 规 范 化 后 的 系 统 网 损、电 压 越限偏差；ω为系统节点电压越限偏差的权重系数；φij，t为t时刻节点i与节点j的电压相角偏差；Vi，t、Vj，t分 别 为 节 点i、节 点j在 调 度t时 刻 的 电 压；Vi，t，min、Vi，t，max分 别 为 节 点i在t时 刻 电 压 的 最 小 值、最 大 值；Gij、Bij分别为支路ij的电导、电纳。

在MADRL 框架下，利用POMG 对PV 集群的实时VVC 模型进行表征。在包含M个智能体的POMG 模 型 中，观 测 空 间O={o1，o2，…，oM}和 动作空间A={a1，a2，…，aM}分别对应于集群VVC 中的状态变量和决策变量。基于当前环境状态S下的观测空间om，每一个智能体通过其策略πm制定其动作am。下一个状态利用传递函数，通过规则P:S×a1×a2×…×aM→S′获取，进而各智能体获取其奖励Rm。奖励函数采用折扣系数γ来平衡当前和未来的奖励，则在时间段T内的预期奖励模型如式（27）所示。

式 中:rm，t为t时 刻 集 群m的 奖 励；γt为t时 刻 折 扣系数。

配电网实时VVC 转化为POMG 形式的过程中，各集群的控制中心为独立的智能体，配电网则为相应的环境，各智能体与环境进行交互以达到训练的效果，从而将原始的实时VVC 模型转化为POMG 形式。

观测空间om包含了集群m的实时动态信息，包含 有 {Vi，t，pi，t，PV，pi，t，PD，qi，t，QD，qi，t-1，PV，qi，t，CB，Tt，OLTC}，其 中，Tt，OLTC为t时 刻OLTC 的 挡 位。OLTC 和CB 的动作决策将直接影响该阶段PV 的无功出力决策，是观测空间中的重要因素，t时刻智能体m的动作决策am，t如式（28）所示。

式中:πm(·)为智能体m的策略；sm，t为智能体m的状态；θm，π为深度神经网络参数；N(0，σm，t)为训练过程中增加的噪声，该噪声服从均值为0、标准差为σm，t的正态分布。

基于式（23）构建相应的奖励函数，如式（29）所示。

通过智能体与环境的交互完成训练过程，本文中的环境为配电网潮流模型的运行约束条件。相应地，状态-动作值函数可以表示为式（30）的形式。

式中:a为当前动作；S′为下一步的状态；a′为下一步的动作；mQπ*(S′，a′)为下一步能够得到的最大状态-动作值；r(S，a，S′)为在当前状态S下进行动作a后获得的奖励。

3 求解算法

3.1 N-ADMM 求解策略

为提高配电网日前VVC 模型的分布式求解速度，本文采用 Nesterov 加速梯度（Nesterov accelerated gradient，NAG）［23］对ADMM 的 对 偶 变量更新规则进行了改进，提出了N-ADMM 求解策略，通过历史迭代信息的挖掘和利用，提高收敛速度。

针对多个智能体间的信息交互，引入辅助变量ui(c)={ui，t(c)}，∀i∈G。

通过引入辅助变量ui(c)与对偶向量λi(c)={λi，t(c)}（即拉格朗日乘子），且∀i∈Gc，可将式（1）改可写为以下形式:

式中:x(c)、X(c)分别为集群c的决策变量、可行域；Lc为增广拉格朗日函数。

式中:ρ为罚参数；bi，t(c)为节点i的边界条件。通过上述拉格朗日函数可将配电网各集群解耦，集群c的VVC 模型可写成式（35）的形式。

设k为迭代次数，N-ADMM 算法求解过程如下。

步骤1:更新决策变量x(c，k)。由于配电网的各集群通过拉格朗日函数解耦，每个区域的决策变量可以通过求解式（36）得到:

式中:ui(c，k)为迭代k次的辅助变量；λi(c，k)为迭代k次的对偶向量。

步骤2:更新辅助变量ui(c，k)。根据步骤1 中所得结果更新辅助变量，如式（37）所示。

式 中:bi，t(c，k)为 迭 代k次 后 节 点i的 边 界 条 件；bc，t(i，k)为迭代k次后集群c的边界条件。

步骤3:更新对偶变量λi(c，k)。基于NAG 法改进对偶变量的更新规则，将传统ADMM 中k－1 迭代的信息权重从1 增加到1+k/（k+3），并引入了k-2 次迭代的对偶变量信息，从而加快了求解速度。

步骤4:判断收敛。若满足收敛条件，则输出结果，算法结束；若不满足收敛条件，则更新迭代次数k=k+1，并转到步骤1。算法的收敛条件如式（40）所示。

式中:τ为预定义的较小的正数，代表算法的容忍度；r(k)、s(k)分别为原始残差、对偶残差。

上述加速的ADMM 不需要集中式的中央协调中心，通过不同区域之间的简单边界信息交换，即可实现各区域在本地求解模型，交替迭代求得最优解。同时在迭代求解的过程中能够充分利用辅助变量和对偶变量的历史信息，加快模型的求解速度。

3.2 改进MADDPG 算法

本文所用MADDPG 算法基于Actor-Critic 的架构，每个智能体均包含一个Actor 网络和一个Critic网络。Actor 网络基于当前状态和训练策略生成动作，Critic 网络通过时间差分计算对Actor 网络进行评估，通过两个网络的相互配合，不断更新迭代，从而获取最大化奖励下的策略。

在深度神经网络的实际训练过程中，智能体m的确定性策略梯度∇θm J(μm)如式（43）所示。

式中:μm为智能体m的连续策略；J(μm)为智能体m的策略μm的性能度量；Qm(S，a)为输入动作a和观测空间O后的状态-动作值函数；D表示经验回放缓存区。D中包含元组{S，a，S′，r}，分别表示状态集、动作集、下一状态集、奖励集，被用于记录所有智能体的经验。在智能体与环境的交互过程中，Critic 网络的损失函数如式（44）所示。

式中:μ′m={μθ′1，…，μθ′M}为目标网络策略集，其中，θ′m为延迟策略参数。Critic 网络通过减小损失来更新网络参数，Actor 网络通过策略梯度来更新网络参数。

在训练MADDPG 的过程中，采样数据集会出现模拟功率超出线路载荷等现象，进而造成算法求解失败，导致模型训练终止，影响收敛速度。针对该问题，本文提出了一种迭代终止惩罚函数，在求解失败的训练集中增加与该集训练持续时间相关的奖励因子。

式中:rm，f为智能体m的惩罚奖励值；fm为固定系数，其为值较大的正数；tm，f、Tm，f分别为终止发生前的训练时间点、训练时间段；tm，max为某一数据集训练的最大时间；Θm为惩罚系数，其等于最大惩罚数值与某一数据集训练最大时间的比值。分析式（46）可知，当在某一数据集训练中不发生终止时，该惩罚量为0，不会对网损降低、电压越限减小的目标函数奖励造成影响。与之相反，当训练过程中发生迭代终止时，该奖励函数会形成一个较大的负反馈，且训练完成度越低，该负反馈越大，从而提升收敛速度。

基于这个终止惩罚函数，智能体m的总奖励R′m如式（48）所示。

3.3 基于MADDPG 算法的训练流程

基于改进MADDPG 算法，本文构建数据驱动的配电网实时VVC 模型，模型训练的基本流程如附录A 图A1 所 示。

首先，设置Actor 网络和Critic 网络参数，输入OLTC 和CB 的动作决策，基于PV 出力、负荷数据、系统网络参数等配电网实际运行状态，形成训练所用数据集。针对每一个训练数据集，某一智能体m根据观测到的观测空间om给出动作am，实现对其管辖范围内PV 出力的控制。进而，结合当前状态S与环境进行交互，即进行潮流计算获取下一状态S′和全局奖励r。各智能体均可获取各自区域的观察结果和系统的全局奖励，同时数据组{S，a，S′，r}被添加到经验回放缓存区，并利用梯度策略更新Actor网络和Critic 网络。重复上述过程，直至训练终止。

4 算例分析

为测试所提模型的有效性及算法的收敛性，本文基于MATLAB 2018b 和PyCharm 软件平台进行了算例仿真。第1 阶段，日前VVC 编程基于Yalmip工具箱；并调用Gurobi 求解器进行了求解；第2阶段，日内实时VVC 的离线训练中调用PandaPower［24］工具箱进行潮流计算与求解。

4.1 算例介绍

本文所用算例系统为标准的IEEE 123 节点系统，其电压的安全范围设置为［0.95，1.05］p.u.。该系统内加装了OLTC、CB 以及PV 来验证所提模型-数据联合驱动VVC 策略的有效性，设备的参数如表1 所示。用于仿真的有功负荷数据来源于葡萄牙某地区的实际数据，PV 的有功功率数据来源于比利时电网运营商Elia 集团［25］，PV 和负荷的有功功率如附录A 图A2 所示。本文采用了文献［9］中DPV 集群划分方法，基于集群划分的IEEE 123 节点系统拓扑参见该文献，PV 集群划分不是本文研究重点，故此处不再进行赘述。

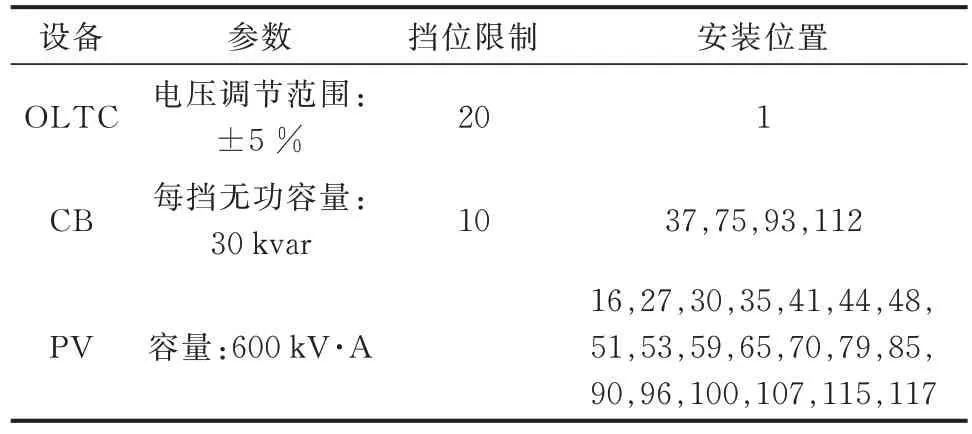
表1 OLTC、CB 和PV 机组参数Table 1 Parameters of OLTC, CB and PV

4.2 N-ADMM 收敛性分析

为验证所提N-ADMM 的收敛性和加速效果，本文引入传统ADMM（traditional ADMM，TADMM）进行了对比分析。两类算法的初始辅助变量、初始对偶变量以及罚参数均采用同样的设置方法，分别为［1；1；0；0；0；0］、0 以及0.5，收敛迭代标准均设置为10-4。

对配电网日前VVC 模型进行求解，N-ADMM与T-ADMM 的残差迭代曲线如图2 所示。

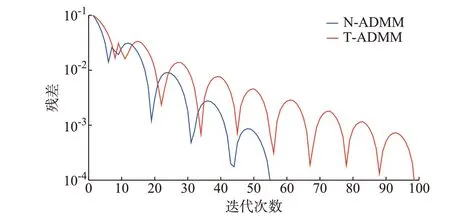
图2 N-ADMM 和T-ADMM 迭代过程对比Fig.2 Comparison of iteration processes between N-ADMM and T-ADMM

分析图2 可知，T-ADMM 需要99 次迭代达到收敛，即残差小于10-4。而N-ADMM 经56 次迭代即可达到收敛标准，与T-ADMM 相比，N-ADMM具有更快的收敛速度。对于高比例PV 接入的配电网而言，N-ADMM 在求解VVC 问题时的表现更为高效，其对配电网日益增长的规模具有更强的适应性。基于N-ADMM 的对偶变量与目标函数迭代过程如附录A 图A3 所示，在迭代初期对偶变量和目标函数的数值曲线均表现出振荡的特征，随着迭代的振荡逐渐减小，并且在56 次迭代后趋于稳定，与求解过程中算法的收敛表现相一致，进一步表明了本文所提N-ADMM 的快速收敛特性。

4.3 配电网日前VVC 效果

基于上述N-ADMM 求解，获取第1 阶段离散设备OLTC 和CB 的动作决策，如附录A 图A4 所示。同时，结合潮流计算求取了采取第1 阶段调控前后系统的电压分布，如图3 所示。由附录A 图A3 可知，在00:00—07:00 以及19:00—24:00 时间段内，OLTC 的挡位决策最高，这是由于该时间段内PV集群出力较低，对于电压的抬升作用有限，OLTC 处于高挡位以降低整个调度周期内的系统网损。随着PV 出力的增加，OLTC 的挡位逐渐降低，在12:00—15:00 时间段内其挡位最低，与该时段内PV 出力最高相一致。

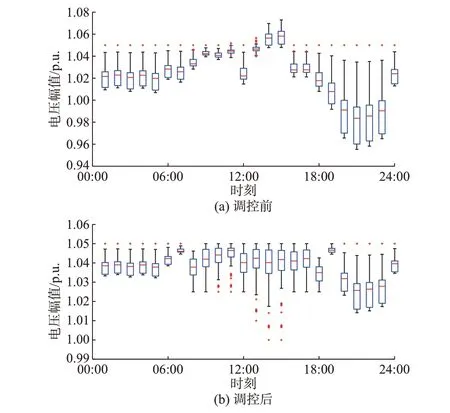
图3 IEEE 123 节点测试系统节点电压分布对比Fig.3 Comparison of node voltage distribution in IEEE 123-bus test system

分析图3 可知，在进行VVC 调控之前，系统出现了明显的电压越上限问题，主要集中在PV 出力较高的时段；节点最高电压幅值为1.073 p.u.，出现在15:00。经过VVC 调控，系统电压水平有明显改善，电压分布在安全范围之内，系统最高电压幅值同样出现在15:00，其最高值为1.05 p.u.。调控前的最小节点电压幅值为0.955 p.u.，出现在21:00，这是由于该时刻PV 出力为0 且负荷处于较高的水平。在VVC 调控后，节点最小电压幅值为1.00 p.u.，出现在14:00 和15:00，这是由于这两个时刻的OLTC 挡位最低。经过VVC 调控，系统网损由2 175.084 kW·h 降低为1 728.052 kW·h。由上述分析可知，第1 阶段VVC 可以有效降低系统网损，同时缩小电压的分布范围，降低了电压的波动水平。

4.4 配电网实时VVC 效果

以全局优化VVC 的离散设备决策和PV 与负荷的数据集、系统网络参数为输入量，基于改进的MADDPG 算法对各智能体进行离线训练。离线训练总共进行了3 000 回合，并且经过2 360 回合后收敛，随着训练的进行，奖励函数的数值逐渐趋于稳定。同时，采用本文所提迭代终止惩罚函数时，相比于传统的固定惩罚值具有更高的收敛速度，特别是在训练的初期体现更为明显，这是由于训练初期惩罚函数形成的负反馈绝对值更大。训练完成后的智能体，可以根据实时观测量制定控制决策，本文所提策略的在线响应速度为18.61 ms，满足PV 集群的实时控制要求。

为针对实时VVC 的效果进行分析，本文选取了2014 年7 月13 日一天的数据进行在线测试，测试中的部分PV 无功功率如图4 所示。

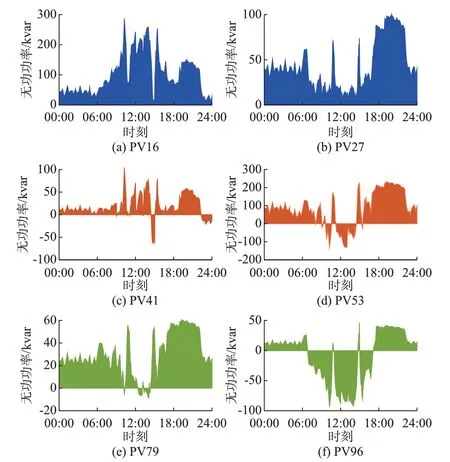
图4 PV 实时控制决策Fig.4 Real-time control decision-making of PVs

分析图4 可知，位于集群1 的PV16 在整个调度周期内发出无功功率，且其高于PV27，这是由系统运行网损最低目标和OLTC 挡位设置等因素共同决定的。由于PV 集群在中午时段会发出大量的有功功率，导致电压的抬升乃至越限，与OLTC 节点电气距离较远的PV53（位于集群3）和PV96（位于集群4）会吸收大量的无功功率，来降低电压水平。同时，综合分析图4 可知，随着PV 有功功率的实时波动，各PV 的无功出力决策自适应变化，证明了MADRL 用于实时VVC 策略的可行性。

为充分验证本文所提方法的有效性，利用传统VVC 策略与本文所提方法进行了对比分析。用于对比的传统VVC 策略采用了与所提策略一致的多级框架与全局优化方法，区别在于采用了传统的QV下垂控制进行PV 无功功率的实时调整。同时，为了充分保证对比的有效性，PV 无功出力基准值的制定时间设置为15 min。两类方法下的部分节点电压对比如图5 所示。

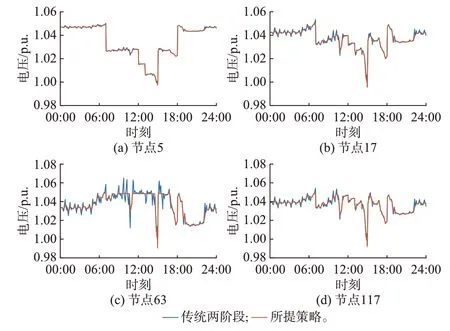
图5 测试系统部分节点电压对比Fig.5 Comparison of partial node voltages in test system

分析图5 可知，对于电压越限风险较低的节点（如节点5），两类方法的效果差异不明显，而对于电压越限风险较高的节点（如节点63），本文所提策略具有明显的优势。这是由于传统的两阶段调控下，下垂控制仅面向单一PV，且需要设置数值较小的下垂系数以保证控制的稳定性，导致其调节能力有限。而本文所提方法可以从全局的角度出发，实现多个PV 间的协同，从而表现出更好的调节能力。除此之外，传统两阶段策略下，第2 阶段的下垂控制以第1 阶段决策值为基准，依赖局部信息进行本地控制，并未考虑2 个阶段决策的相互影响，2 个阶段运行决策的协调性不足；而本文所提模型-数据联合驱动方法，在第2 阶段的实时VVC 训练过程中以第1 阶段的离散设备决策为输入量，通过大量的数据训练对实时动态运行工况进行模拟，从而充分保证了第2 阶段与第1 阶段决策具有更好的协调性。与此同时，传统的两阶段策略下，系统网损为1 702.537 kW·h，采用本文所提策略时，系统网损降为1 615.773 kW·h，证明了后者更为优异的降损效果。

5 结语

随着DPV 在配电网中接入比例的不断提高，基于集群划分进行的分布式VVC 能够有效引导PV的可靠、有序、安全、经济并网。本文提出一种适用于DPV 集群的配电网模型-数据联合驱动VVC 策略，利用模型优化进行日前调度以保证决策的可靠性、全局最优性，利用DRL 进行日内PV 的实时控制，以充分发挥其毫秒级响应速度的优势，实现对PV 无功出力的实时自适应调控。

电力系统的模型中蕴含了大量的运行规律与有益的信息，如下垂控制本质为电压-无功功率的关系规律，潮流模型雅可比矩阵包含梯度信息等，充分挖掘该类信息和规律可以有效降低强化学习对于数据的依赖性，这也是本文后续的研究重点。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。