数学知识与思想方法在初中物理解题中的应用
2024-05-16朱春云
朱春云


【摘要】把数学知识与思想方法用于初中物理解题中,对学生更好理解题意、降低解题难度、高效快速准确解题,以及提高学生物理解题创新能力具有重要意义.因此,教师要充分认识利用数学知识与思想方法解题的意义,指导学生根据不同的问题,选择适当的数学知识与思想方法,合理建立物理问题与数学知识与思想方法的联系,提高学生利用数学知识与思想方法解决物理问题的能力.
【关键词】数学知识;初中物理;解题应用
数学与物理两学科有着密切的联系,两者相互联系、相互渗透.把数学知识与思想方法应用到初中物理解题中,能更好地帮助学生理解物理问题的本质,降低物理解题难度,丰富学生物理解题方法策略,对提高学生物理解题能力和物理学习成绩有重要意义,因此在初中物理解题教学中,要注重渗透利用数学知识与思想方法解题策略.
1 数学知识与思想方法在物理解题中应用的意义
将数学知识与思想方法应用在初中物理解题中,无论对提高物理解题能力还是促进学生物理核心素养发展等都有重要意义.
一是能够进行精确定量分析.物理解题过程中,常常需要对问题进行精确定量分析.利用代数、几何等数学知识,能帮助学生对物理量进行精准量化分析和表示,为解题提供支撑.
二是有效降低物理解题难度.物理解题中很多问题和计算过程可以通过数学知识方法进行简化处理,有效降低问题难度,使学生在物理解题中游刃有余,能够提高物理解题效率.
三是提高学生综合解题能力.数学知识与思想方法在物理解题中的应用,可以锻炼学生运用跨学科知识与思想方法解决物理问题的能力,從而有利于提高学生物理综合解题能力.
四是培养学生解题创新思维.数学知识与思想方法在物理解题中的应用,能启发学生解题思路,让学生尝试从数学知识与思想方法的角度解决物理问题,有助于培养学生解题创新思维.
2 数学知识与思想方法在物理解题中应用的策略
2.1 应用数学知识解决初中物理问题
在初中物理解题中,通过应用函数、方程、不等式、比例等代数知识,直角三角形、相似三角形等平面几何知识,以及数学公式、定理等数学知识,既能降低解题难度,快速有效形成解题思路,又能简化解题过程、提高解题准确性.
例1 已知R1是20Ω 的定值电阻,R2是1A、60Ω 的可变滑动电阻,把两者串联后接到恒定电压为6V的电源上,求R2能产生的最大功率是多少?
解析 由于电源电压U与R1数值不变,R2的阻值和获得的电压会根据滑片滑动情况发生变化,会导致电路中的电流I随之变化.当R2的阻值变大时,电路的电流I会减小;当R2的阻值变小时,电路的电流I会增大.要计算R2产生的功率,可利用P=IU计算,但I和U两个量都是变化的,且一个增大时另一个减小,应用正常的方法无法计算其最大功率.如果利用数学知识就容易计算.用Rx表示R2滑动时的实时电阻值,则I=UR1+Rx,滑动变阻器R2上的功率为P2=I2R=U2Rx(R1+Rx)2=U2(R1+Rx)2Rx.观察此式可看出,在电压U不变的情况下,只要(R1+Rx)2Rx取得最小值,那么P2就可获得最大值.将此式利用数学完全平方公式进行变形可得,(R1+Rx)2Rx=(Rx-R1)2Rx+4R1,由于(Rx-R1)2≥0,只有当Rx=R1=20Ω时,R2才能得到最大功率,即P2=62(20+20)220=0.45W.由此可见,本题通过应用数学完全平方公式、不等式等知识,使复杂繁琐的解题过程变得简单容易,从而能提高解题效率.
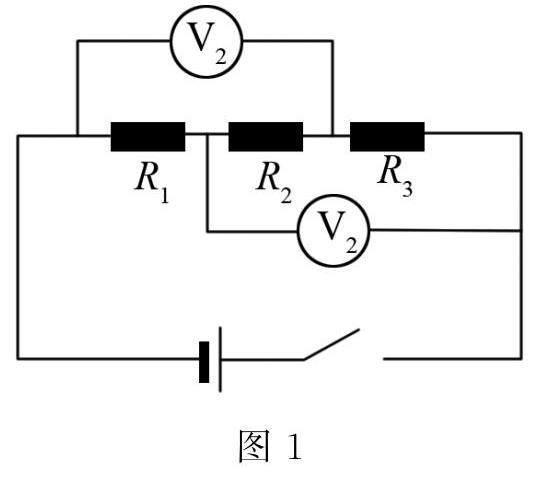
例2 已知三个电阻R1=20Ω,R1=40Ω,R3=50Ω,如图1所示,求两个电压表示数之比是多少?
解析 由于电压U与电阻R成正比,在本题中三个电阻串联,它们的电流相同,电源电压不变,因此本题可利用数学比例知识进行求解.U1U2=R1+R2R2+R3=20+4040+50=23.可见通过应用数学比例知识,使本题既省去繁琐的计算,又变得非常简单.在本题中运用了正比例进行物理解题,在其它物理解题中还可以利用反比例法解题.如:两汽车在相同公路上行驶的速度之比是3∶4,当两汽车行驶相同的路程时,求它们所用时间之比是多少?根据速度公式v=st可知,在路程固定时速度v与时间t成反比,因此可知它们行驶相同路程的时间之比为4∶3.
2.2 应用数学思想方法解决物理问题
把数学思想方法用于初中物理解题,有利于直观形象地反映物理问题的本质,能有效降低抽象复杂物理问题的理解难度,使解题过程更全面,还能够使物理解题方法多样化,因此在物理解题中,教师应指导学生根据问题类型,选择合适的数学思想方法,并注重将物理问题与数学思想方法建立联系,才能有效发挥数学思想方法在物理解题中的应用价值.
例3 有一个容器装满水,将一个物体放入容器中,溢出水的质量是200克,求该物体的质量是多少.
解析 在求解本题时,不能简单地应用力等于物体排水的重力进行简单计算,因为在本题中,不能确定物体放入容器后的状态是“沉入容器底部”“悬水中间”,还是“漂在水上”,因此需要利用数学分类讨论思想分三种情况进行解答:(1)当“物体沉入容器底部”时,该物体的受力情况是G物>F=G排,因此该物体质量大于200克;(2)当“悬水中间”时,该物体的受力情况是G物=F=G排,因此该物体质量等于200克;(3)当“漂在水上”时,该物体的受力情况是G物=F=G排,因此该物体质量等于200克.通过对三种情况的分类讨论,可以确定该物体≥200克.通过应用数学分类讨论思想方法,使本题的求解更全面,提高了解题准确性.
例4 有一个金属块A和木块B,木块的体积是金属块体积的5倍,分两种方式将两者放入盛水的容器中.方式1:把金属块A放在木块B上,恰好使木块浸入水中,如图2-1所示.方式2:把金属块沉入容器底部,并且容器底部对其支持力为3N,木块处于静止状态且有25在水面之上,如图2-2所示.求金属块A和木块B各自的重量为多少?(g取10N/kg)
解析 本题的求解如果运用分步计算的方式比较繁琐,而利用数学方程思想方法进行求解就比较简单.可根据物体受力平衡原理,建立一个方程组就可使该问题得到快速有效解决.可根据两种情况建立如下三个方程并联立成方程组:
F1=GA+GBFB=GBFA+F支=GA
ρ水gVB=ρAgVA+ρBgVB①ρ水g1-25VB=ρBgVB②ρ水gVA+F支=ρAgVA③,
根据方程②可求出ρB=0.6×103kg/m3.
将VB=5VA代入方程①中,能求出ρA=2×103kg/m3.把ρA代入方程③,能求出VA=2×10-4m3,可求出GA=ρAgVA=2×103×10×2×10-4=4N,GB=ρBgVB=6N.由此可见通过应用数学方程思想方法,使该问题得到快速解决.
此外,数形结合思想方法、转化思想方法、整体思想方法等也都是物理解题经常使用的数学思想方法,在物理解题中都发挥着特殊重要的作用.
3 结语
总之,把数学知识与思想方法应用于物理解题中,对提高学生解题能力和物理成绩具有重要意义.在初中物理教学中,教师要注重指导学生积极尝试利用数学知识与思想方法解决物理问题,特别是解决复杂抽象、繁琐的物理问题,能提高物理解题效率和正确率.同时教师还要指导学生对利用数学知识和思想方法解决物理问题的经验进行总结,形成自己的解题方法策略,就能使数学知识与思想方法在物理解题中发挥更大作用.
参考文献:
[1]柏兆明.数学知识在初中物理解题中的运用[J].科普童话,2020(01):20-21.
[2]李建录.浅谈数学方法在初中物理解题中的应用[J].数理化学习,2019(07):62-63.
