数学方法在初中物理解题中的应用
2024-05-16张凤翔
张凤翔


【摘要】 随着社会的发展,各界人士愈发关注教育事业,并强化了在学生综合素质方面的培养.初中物理学科具有较强的逻辑性,注重学生逻辑思维能力的考查.在具体的解题过程,当遇到相对复杂的问题时,应整合数学思维方法,以此增加解题便利性,提升问题解析的精准性.下面,笔者将围绕初中物理学科展开探讨,主要探讨数学方法在实际解题过程中的应用问题.希望能为初中物理教学提供参考.
【关键词】数学方法;初中物理;解题教学
长期以来,因应试教育的作用,致使广大学生在物理学习中的兴趣不是很高.而物理学科主要探究物质的结构和运动规律,为保证整体的学习效果是理想的,一定要让学生全面掌握数学知识,巧妙运用数学技巧.为此,教育工作人员务必要加大相关重视,把数学知识合理应用到物理解题中,让学生具备利用数学知识来解决实际物理问题的能力.
1 数学方法在初中物理解题方面的应用情况
在当前的教学活动中,物理教师开始倾向把数学知识与物理知识融合到一起,将数学方法引入到物理解题活动中.现下,物理教学以解题为重点,主要想通过不同的知识来完成问题的解答.然而,因物理与数学之间存在显著的关联性,整合数学与物理知识比单一应用物理知识进行解题要更有效,尤其是对于某些复杂问题,单纯应用物理知识会更加繁琐,且不便于学生的消化理解,由此不难发现,应用数学知识可在某种程度上简化物理解题.
2 数学方法的应用意义
数学方法是一种研究工具,能够完整表示速度、密度等不同的概念.同时,数学方法还能把物理学问题经由抽象与推理加以整合,以此转化为规律性定理,即便在实验和实践等不同环节还可融入数学方法,以此促进物理学习.在物理教学实践中,时常会因在概念与规律方面掌握不完全而引发不理解解题思路的问题,但数学学科可培养学生的逻辑思维,锻炼其解题技巧,全面应用数学知识能够进一步明确物理解题原理.
3 数学方法的应用优势
3.1 具有相同区间
数学和物理都具有较强的逻辑性,物理与数学问题的各个解题步骤之间紧密相连,经由前一步可推算出下一步,从本质层面来说,这两者的解题存在相似,无论通过何种方法来解题,最终获得的答案都是相同的,且是惟一的.由此可知,可利用某些数学方法来解决物理问题.
3.2 有利于理解物理概念
物理概念包含质和量这两种,其中质涉及运动、静止,量则包含速度、密度.同时,物理的分式模式和数学运算密切相关,它将其中一个物理量看做分母,再取相同单位数量,将另一个物理量看做分子加以比较.利用数学思维来学习物理概念,有利于更好的把握知识的内涵.
3.3 有利于掌握物理定律
物理除了公式和定义,某些计算方式需要利用图像来解决.众所周知,解析式与文字表达呈现的内容是一样的,然而,解析式更便于理解.将物理问题转化为数学问题能够使问题快速解答.如“晶体与非晶体”熔化内容的比较,本节内容不便理解,此时可将熔化温度与时间用图象呈现出来,利用图像加以比较,便易于掌握.为此,物理学习应具备一定的数理结合意识,要培养学生此种意识的自主性.
4 用数学方法解决物理问题剖析
4.1 借助图像解决问题
某些物理問题与现象较为抽象,不便掌握,更不能有效理解涉及的问题.若用图像进行表述,则可将抽象的知识直观化,还会降低难度.例如,学习“光的折射”内容时,可通过水杯、水与铅笔加以演示,待学生看到水中所呈现的铅笔形状以后,让学生将其画出来,此种实践与图像紧密结合的方式可让学生对物理知识形成清晰的认知,加深记忆,主动学习物理知识.然而,应用图像来解决问题时,务必要保证作图精准,否则会适得其反.
4.2 利用实践证明结论
学生升入初中以后,便会开设实验课,把文字理论知识变成实践活动,以此来加深学生的记忆.在实验课堂上,学生应带着笔和本子,记录实验数据,随后对上述数据进行整理,做成表格,以便观察和对比.当学生看到记录的数据,在大脑中会形成反应,找到共同点.以“电阻”内容为例,本节主要应明确电流、电压和电阻这三者之间的关系,在实验课堂上,教师应组织学生开展多次实验,并认真记录对应的实验数据,最终验证欧姆定律的正确性,此种实践方式既能提升学生的主动性,也能让学生高效记忆知识点.
4.3 利用方程解决问题
首先剖析物理问题现有的已知条件与未知条件,确立这两者之间的关系,然后列出等式.如果物理问题相对复杂、不易解答,则可结合数学知识进行解答,其中最为常用的便是方程组.待列好两边关系以后,便可知有一个数值未求解出来,此种直观的方式大大提升了解题效果,并增大了解题的正确率.
5 数学方法的具体应用
5.1 极值知识在物理解题过程中的应用
分析解题思路时,应明确物理量的对应关系,它们之间往往相互制约,当其中一个变量发生变化,则别的变量也会表现出一定的变化,此时,可能会应用到极值内容.依托数学思维来剖析物理题目,可能会增加剖析过程的有效性,推动解题.但在初中物理解题过程,应用极值法时大多会引入一元二次方程极值.
例如 如图1所示,电源电压为9V,灯泡L的规格为“6V、6W”,滑动变阻器,R的最大电阻值为20Ω,灯丝内部的电阻始终不变.闭合开关以后,推测滑动变阻器电阻处于3~20Ω的最大功率.为完成本题的求解,教师应启迪学生运用极值法完成解答.调节滑动变阻器时,电流和电压都会表现出对应变化的小灯泡电阻值是626=6Ω,滑动变阻器两端电压是U-IRL,随后得出滑动变阻器的功率P=I×(U-IRL)=-6(I-34)2+278,可知当I为34A时对应的功率最大是827W.
5.2 几何知识在物理解题过程中的应用
在初中阶段,旨在通过物理学科的教学来强化学科素质、提升综合能力,不单纯要应用物理实验等常用的教学方法,也应强化和其他学科的有机整合,适当调整学生的思路,借助多种工具完成题目的解答,实现知识的迁移,促进学科素质的提升.物理与数学离我们的生活较近,在日常生活中随处可见物理与数学知识的实际应用,由此不难发现,这两个学科紧密相连.在实际教学中,不要刻意凸显各个学科的界限,有时候应巧妙应用其他学科的思维,以此推动本学科的教学,提升解题成效.某些物理题目可能存在特定条件,要求基于实际取值妥善处理.运用几何知识,能够让物理题目直观地呈现出来,简化解题过程.
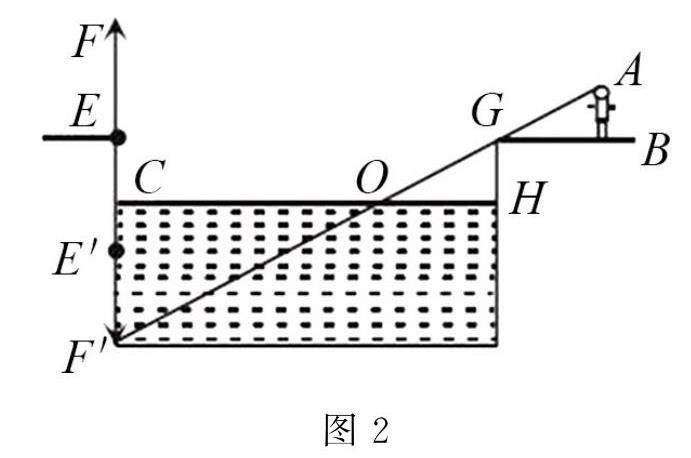
例如 有一条小河,某人站在河边看对岸有一颗树EF,其在水中的像较为清晰和完整,当人一点点后退,超过6m便无法看到完整的树像.假设此人的身高是1.8m,河两岸都高出水面1m,河的宽度是40m,试计算树高是多少.依照题意可知本题主要考查平面镜成像原理,然而,若想高效、简化解答,则应引入相似三角形和对称知识.设定树EF在河中所形成的倒影是E'F',三角形COF'和BGA、HOG是相似三角形,经此可知,COCF′=OHGH=GBAB,将已知数值带入其中,可得出CF'是11m,由于河两岸均高出河水1m,最终得出EF是10m.
5.3 函数图像在物理解题过程中的應用
在物理解题中,应用函数图像,主要是通过函数图像来呈现物理信息,它可直观地表达物理规律.如小红骑自行车、小丽跑步,二人的运动路程随着时间的推移也在发生着变化,当运行至100m时,小红的速度是4m/s,小丽的速度是2m/s,请问两人是否同时出发,小红前进100m所耗用的时间是多少,小红和小丽的速度均是多少(m/s).以上是物理题目中较为常见的题型,此类题目主要通过函数图像来表达物理量的内部关系.学生如果想解决这一问题,则应引入函数图像内容,即通过函数图像剖析物理量的对应关系,以此明确动态变化过程,有效利用已知数值完成求解.
6 数学方法的应用注意要点
在初中物理解题过程中应用数学方法,能够增强学生思维,有效解题,但为将数学方法的作用完全发挥出来,应注意以下几点:
其一,明确数学思维和物理概念、定理认知之间的关系.从解题层面而言,数学方法较为有效,为此,学生应明确数学思维和物理概念的之间,特别是数学思维在实际应用过程中所表现出的局限性.为有效解答物理问题,应指导学生借助数学知识来完成解题,首先应确立题意,找到包含的物理概念和定律,可查阅教材,也可回忆,弄清物理知识,挖掘问题背后隐藏的知识点,科学选用数学方法,杜绝死记硬背.
其二,加强物理单位的备注,深化在物理单位方面的理解.在借助数学方法对物理问题进行解答时,备注物理单位十分必要.只有先备注,才能理解,从而全面认识与理解,选取恰当的数学方法来解题,规避在解题步骤或者单位换算过程中出现不良问题.因此,为保证解题精准度,带领学生通过数学方法来解答问题,在此过程务必要备注物理单位.
7 结语
综上可知,要想学好物理,则首先应学会数学,这是因为物理知识包含较多的数学知识,广大教师在开展物理教学时,既要全面准备物理知识,也应了解学生的数学学习情况,基于此,把数学知识和物理教学紧密整合到一起,让学生利用数学知识合理解决物理问题.长此以往,学生的物理学习兴趣会一点点升高,最终的物理学习成效也会大大提升.
参考文献:
[1]石如勇.论数学方法在初中物理解题中的应用[J].百科论坛电子杂志,2023(13):571.
[2]胡华南.探究数学方法在初中物理解题中的应用[J].新教育时代电子杂志(教师版),2023(8):102.
[3]张知礼.运用数学知识解决高中物理问题的教学研究[J].读与写,2023,18(4):178.
[4]徐玉亮.浅析初中数学教学中数形结合思想的应用[J].科普童话·新课堂(下),2021(3):31.
[5]刘鹏.摭谈数学知识在初中物理解题中的应用[J].数理天地(初中版),2022(4):45-47.
[6]潘玮.建模探究润物无声——初中数学建模教学课堂片段评析与反思[J].中学数学,2022(6):90-91.
[7]崔德.刍议“建模思想”在初中数学教学中的应用[J].中学数学,2023(12):65-66.
[8]龙经良.初中物理解题中渗透数学概念的应用研究[J].人文之友,2022(2):190.
