极限思维法在初中物理解题中的应用
2024-05-16徐华
徐华

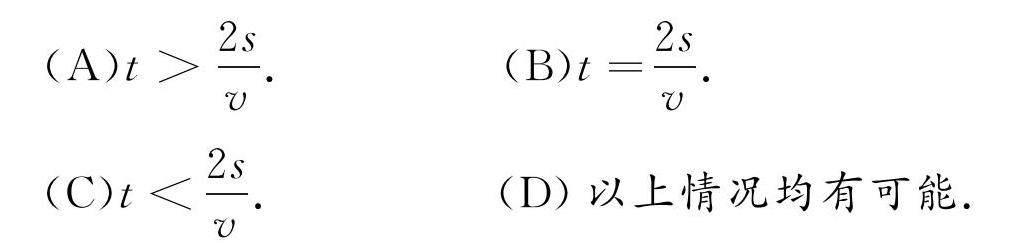
【摘要】在对物理试题求解的过程中,极限思维法是一种比较常用的解题方法.初中物理教师在物理解题教学中,借助极限思维法指导学生进行解题时,能够使学生更好地发散思维,并转变传统固有的思维观念,从而使学生学会运用极限思维的方法对物理习题进行完美的解答.相比于其他解题方法,极限思维解题法能够使初中物理习题化难为易、化繁为简,以此灵活应用从而达到快速解题的目的.
【关键词】极限思维;初中物理;解题应用
在新课改背景下,教育教学过程中对教师的教学要求变得越来越高,而教师想要提高教学质量,则应该在日常的教学工作中不断研究和更新自身以往的教学模式.在初中物理课的教学过程中应用极限思维法时,能够将复杂的物理过程进行分解,可选择整个过程的两个端点和中间的极限对问题进行分析,能够更加直观、简单地解析出物理习题,从而使物理解题变得事半功倍.
1 利用极限思维法寻找问题入口
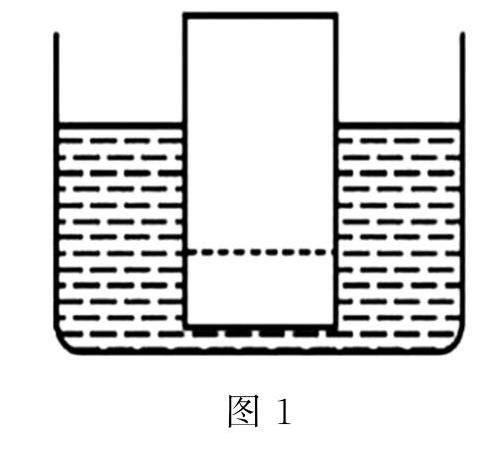
例1 如图1所示,当杯子中盛有一半水时,将木块放入到杯子中,木块的上半部分漂在水面上,而沿着图中的虚线位置将木块下部分截掉,那么剩余的木块位置会发生什么变化?
解析传统解题方式:
在使用传统解题方式时,大部分学生会考虑到木块的密度属于均匀分布,因此认为无论将木塊下半部分如何截掉,木块依旧会有一部分漂在水面,一部分在水下[1].但是木块被截掉后,对应的体积会变小,受到的力也会变小,所以只能判断出相比之前的位置有所下降.
极限思维法解题方式:
采用反向思考的方式,根据题目中的要求,将木块下半部分截掉,木块依旧在水中处于漂状态.但木块自身的密度并没有发生变化,因此,木块的下半部分也一定会浸泡在水中.在解题时,引导学生利用极限思维法,可以快速寻找到解题的切入点,防止出现计算数值繁琐的情况,有利于学生在解题时节省时间.
2 利用极限思维法判断液体压强大小
例2 如图2所示,在甲乙两个量筒中的水和煤油质量相同,随后对甲乙两个量筒中分别选取A、B两点,而这两点与量筒的底部距离相等,设A、B两点的液体压强分别为PA、PB,那么以下四中说法中,哪一种是正确的( ).
(A)PA<PB. (B)PA>PB.
(C)PA=PB.(D)无法判断.
解答该题目,可利用差值法,可以根据公式P=F/S=G/S得出水和煤油对量筒底部的压强相同,所以无论是A量筒还是B量筒中的液体,对量筒底部所造成的压强为不同液柱所产生的总压强之和,所以P水=PA+PA下,P油=PB+PB下,其中PA下和PB下可以比较,并根据P=ρgh.
由于ρ水>ρ油,因此可以得出PA下>PB下,从总压强中减去下段的压强,可以得出P水-PA下<P油-PB下.所以PA<PB,故(A)选项正确.
3 利用极限思维法分析运动学
例3 在一条河上有A和B两点,其中A点处于河流的上游,同时河流上有甲乙两个休息点,甲休息点位于A点位置,乙休息点位于B点位置.当一条船的速速为v时,如果船从甲为起点开往乙位置点后再次返回到甲位置点,整个往返时间用t表示,当甲乙两个休息点之间的距离用s来表示时,以下选项中正确的是哪一项( ).
(A)t>2sv.(B)t=2sv.
(C)t<2sv.(D)以上情况均有可能.
解题思路 在对本道题目使用极限思维解题方法时,由于题目中涉及到了三个不同的物理量,这三个物理量分别是船速v,路程s以及水流速度[2].因此在对题目进行解析时,需要充分考虑对这些物理量进行极限化的分析,当对路程s进行极限化放大时,那么船在来回往返时所需要的时间则会被无限放大,这样的参考并没有任何实际意义.因此在极限思维法中,可以将船速极限放大,那么对应的往返时间则会趋于无限接近,而将水流速度无限放大时,则存在水流速度不能超过船速,否则题目不成立,所以这道题目的极限最大化值只能是船速.
分析 在对该题目进行解题时,传统的解题方式通常需要考虑到船在行驶过程中受到水流速度的影响,因此在计算时,往往会将船的行驶速度和水流速度进行合成,并以此根据甲乙两地的实际距离,船的行驶速度列出对应的表达式进行对比分析,但这种传统的解题方式比较麻烦,只有在教学过程中由物理教师逐渐引导学生使用极限思维的方式,才能实现对本道题目的正确求解.
解题 应用极限思维法:船在逆流返航时与水流的速度合成后为0,那么船必然无法返回到甲休息点,在这种情况下,船来回行驶的时间将会趋于无穷大,所以可以得出(A)选项的答案是正确的.
小结 在运动学中应用极限思维法时,通常需要将整个题目中所对应的物理量理清楚,而本道物理习题中所涉及到的物理量分别有路程s、速度v以及时间t这些变化的物理量,因此学生想要解答这道题目,则需要充分了解这些物理量,同时结合题目中已知的条件选择相应的物理量进行极限化的应用,才能在极限思维分析时将日常生活常识考虑进来,如同本道题目中,水流的速度绝对不可能大于船返回时的速度,否则这样的题目不仅不成立,也没有任何意义.
4 利用极限思维法分析电问题
例4 如果定值电阻和滑动变阻器之间进行串联后形成相应的电路图时,滑动变阻器的电阻变化范围在0~100Ω,当已知定值电阻R0=10Ω时,随着滑片的移动,那么定值电阻两端所对应的电压表读数范围变化是多少?
解题思路 在本道题目的解题过程中,对应的变化物理量为滑动变阻器接入到电路中的电阻值,因此当滑动变阻器在对应的区间范围进行变化时,那么需要考虑到最大值和最小值的情况,即滑动变阻器的电阻为0Ω和100Ω时的结果.
解题 已知题目中的滑动变阻和定值电阻之间属于串联关系,所以当滑动变阻器的滑片处于变阻器两端时,可以得出电压表的示数,而电压表的最大小数为220V.随着滑动变阻器接入到电阻为100Ω的电路中时,由于电路中的电流最小,所以电压表的示数也是最小的,其电压为20V.
小结 由于初中物理中的电学知识具有一定的难度和复杂性特点,因此大部分学生在对这一单元进行学习时,需要结合相对应的电路图才能实现对整体电路知识的深入分析,并得出正确的答案[3].本题中的滑动变阻器与定值电阻之间的关系通常属于并联关系,所以想要求解出滑片所处的位置,则需要电流表的示数达到最大值,对于这种情况的分析,恰好和问题呈现相反的情况,同时所对应的电学问题中出现的相关物理量也并非一成不变.学生在对这种物理问题的求解中,通常需要寻找到准确的区间范围,才能根据相应的物理量对不同区间进行深入分析.
5 结语
通过对以上相关的初中物理例题使用极限思维法进行解题时,能够有效节省解题的时间,相比于传统的物理解题方式,极限思维的解题方式可以使学生对题目了解得更加深入,以此在初中物理知识的学习中,可以更好地实现对不同物理问题解题技巧和方法的掌握.
参考文献:
[1]时华夏.初中物理解题中极限思维法的有效应用[J].数理天地(初中版),2022(08):46-48.
[2]施燕莹.极限思维法在初中物理解题中的运用[J].数理化解题研究,2022(02):88-90.
[3]许奇龙.极限思维法在高中物理解题中的有效应用[J].数理化解题研究,2020(34):75-76.
