在数量、位置的变化中领悟平面直角坐标系

领 "衔 "人：王金坤

组稿团队：江苏省盐城市毓龙路实验学校

函数是初中“数与代数”的核心内容之一，“平面直角坐标系”是我们学习函数的基础和工具。在本章，我们将学习如何用变化的数据描述变化的位置，体会有序数对可以确定物体的位置，认识到表示平面内点的位置需要两条数轴形成一个坐标系。在一个个“数对”和一个个“点”的位置的对应关系中，我们将不断感受“数形结合”思想，发展空间观念。

一、用数量变化确定位置变化

我们知道，每一个实数都可以用数轴上的一个点来表示，数轴上的每一个点都表示一个实数，这样就建立了实数与数轴上的点一一对应的关系。那么，我们能不能用一个实数表示平面内一个点呢？比如，看电影，按照电影票上显示的第4排5号，我们就能准确地找到自己的座位。如果只告诉你座位是第4排或者5号，这样的位置就不确定了，也就是说，一个实数不能描述电影院里某个座位的位置。如果把第4排5号记为（4，5），其中前一个数表示排数，后一个数表示座位号，这样我们就可以用（4，5）来表示电影院第4排5号的座位。同样，我们可以用经度、纬度两个数据确定地球上某个点的位置，比如东经130.7°、北纬19.6°，确定的是东经130.7°线、北纬19.6°线的交点。

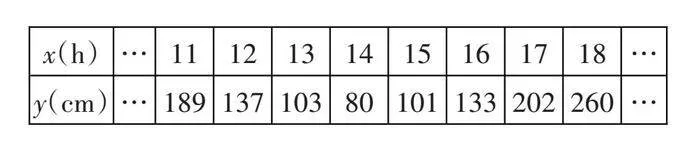
类似的实际问题有很多，如某一天港口的潮水高度y（cm）和时间x（h）的部分数据如下：

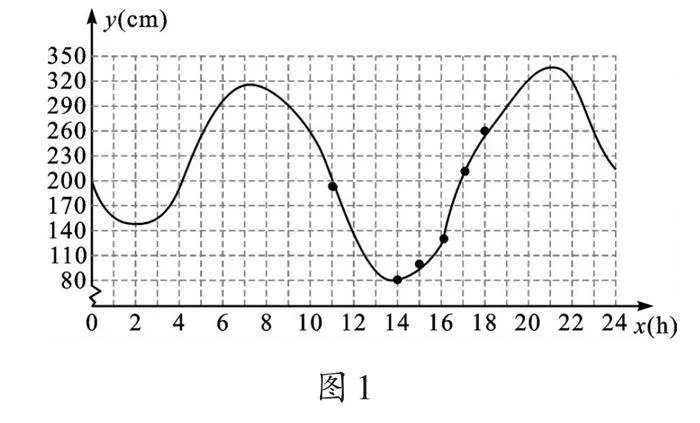
观察表格中的数据，这一天11h港口的潮水高度189cm，12h港口的潮水高度137cm……潮水高度y（cm）和时间x（h）的变化是“数量的变化”，我们发现可以用“数量变化”来描述“位置的变化”。根据表中的数据，通过描点、连线（光滑曲线），得到图1。

这样，又可以用“位置的变化”来描述“数量的变化”，使“数量的变化”更加直观。

二、建立平面直角坐标系，描述点的位置

平面内一个点的位置需用两个实数才能确定，而这两个实数显然不能是同一条数轴上的两个数，那么是不是需要两条数轴呢？

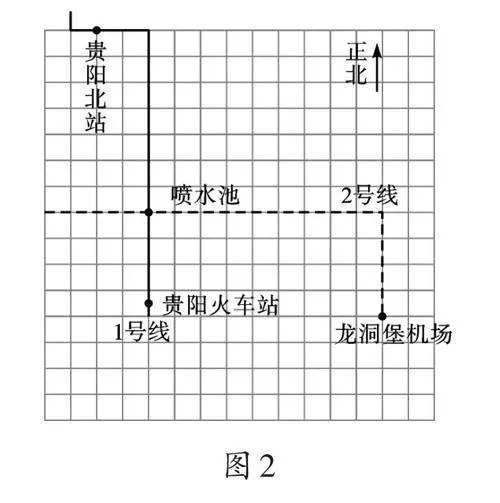
例如，图2是贵阳市城市轨道交通运营部分示意图。我们怎样描述贵阳北站等地的位置呢？

为了表示平面内点的位置，我们通常画两条互相垂直且有公共原点的数轴，构成平面直角坐标系。平面直角坐标系的建立，关键是选取一个适当的原点。建立了平面直角坐标系后，平面内的点就可以用一对有序实数来表示，这样的有序数对称为点的坐标。

在平面直角坐标系中，一对有序实数可以确定一个点的位置；反过来，任意一点的位置都可以用一对有序实数来表示。就像“实数与数轴上的点一一对应”一样，平面上任意一点P和唯一的一对有序实数对（a，b）是一一对应的，其中a是横坐标，b是纵坐标。

三、在图形运动中探索点的坐标

将一些简单的图形置于平面直角坐标系中，进行平移、翻折、旋转，用点的坐标来描述运动后图形的位置，我们就可以探索原来的点与位置变化后所得的点的坐标之间的关系。

如图3，已知点A（1，0）、B（4，3），将线段AB先向左平移3个单位，再向上平移1个单位，得到线段CD，那么我们怎样描述线段CD的位置呢？此时，点C的坐标是（-2，1），点D的坐标是（1，4）。我们发现，点C的横坐标比点A的横坐标小3，点C的纵坐标比点A的纵坐标大1；点D与点B的坐标也有同样的关系。如果点P（m，n）在线段AB上，那么，当线段AB平移到CD后，点P的对应点坐标是（m-3，n+1）。

在上述探索过程中，我们不难发现，运动后的图形与原来的图形的对应点坐标之间存在一定的关系。一个图形沿x轴平移，图形上点的纵坐标不变，横坐标改变；一个图形沿y轴平移，图形上点的横坐标不变，纵坐标改变。同样，一个图形沿x轴翻折时，图形上点的横坐标不变，纵坐标变为原来的相反数；一个图形沿y轴翻折时，图形上点的纵坐标不变，横坐标变为原来的相反数。一个图形绕坐标原点旋转时，横坐标、纵坐标都会改变。

学习了平面直角坐标系后，我们进一步体会到借助平面直角坐标系可以刻画物体的位置，它让数与形之间建立了更加紧密的联系。

（作者单位：江苏省盐城市毓龙路实验学校）