公路护栏中金属空心球泡沫铝防撞性能的研究

符明铎,刘嘉铭,王岩森,姚梦媛,吴鹤翔

(1.东北林业大学土木工程学院,黑龙江 哈尔滨 150040;2.东北林业大学经济管理学院,黑龙江 哈尔滨 150040)

金属材料经过发泡工艺可以制备成兼具金属和气泡特征的金属泡沫材料[1]。金属泡沫材料凭借轻质高能量吸收的特性,作为安全防护和吸声材料应用于土木工程的护栏、屏障、桥墩等结构中[2-4]。由于气泡孔隙位置任意存在于金属泡沫材料中,使其力学性能难以调控。针对这一问题,内部结构均匀、可控的金属空心球泡沫受到了广泛关注[5]。

到目前为止,关于金属空心球泡沫材料静态和动态力学性能的研究已经广泛展开。Yu等以乒乓球作为原材料,开展了均匀空心球阵列的力学性能研究[6,7]。基于功能梯度的概念,国内外许多学者针对多孔材料提出了梯度多孔材料的概念。同均匀多孔材料相比,梯度多孔材料存在降低被保护端冲击力,控制能量吸收过程等优异的力学性能。Zeng等[8]针对金属空心球泡沫材料同样进行了梯度设计,并开展了霍普金森杆的冲击性能实验研究。研究中将金属空心球泡沫分层,同层泡沫的密度相同,不同层泡沫的密度不相同,没有考虑不同密度金属空心球混合排列的情况。

通过建立金属空心球泡沫模型,分析了冲击压缩条件下,不同密度金属空心球混合排列,即不同质量在空间的分布对金属空心球泡沫动力学响应的影响。

1 有限元模型

属空心球泡沫的计算模型如图1所示。试件沿x、y、z方向的尺寸为6l×9l×6l,其中l表示空心球的外直径。此时,金属空心球泡沫的相对密度为

(1)

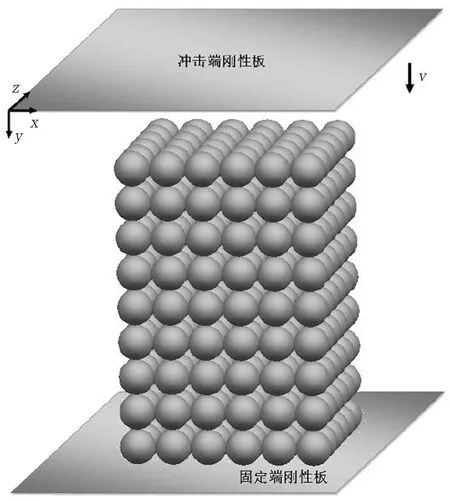
图1 金属空心球泡沫的计算模型

式中:N为空心球的数量,个;hi为第i个空心球的壁厚,m。这里通过改变空心球的壁厚来控制质量在空间的分布。

基于图2给出的4种空心球质量分布方式(图中浅灰色的球壁薄,黑色的球壁厚),分别命名为MBF1,MBF2,MBF3,MBF4。讨论了具有相同相对密度金属空心球泡沫的力学性能。根据公式(1),均匀金属空心球的壁厚hM=0.8 mm,薄壁金属空心球的壁厚hL=0.6 mm,厚壁金属空心球的壁厚hH=1.0 mm。所有金属空心球的外直径l=40 mm。

图2 空心球质量空间排布示意图

采用有限元软件Abaqus对金属空心球铝泡沫材料开展冲击动力学性能的数值模拟计算研究。如图1所示,金属空心球焊接构成金属空心球泡沫,并置于底部固定的刚性板之上,四周自由不设置约束。顶部刚性板以某一初始速度沿竖直方向向下冲击。基体材料选择铝,采用理想弹塑性模型。材料参数设置为:密度ρ=2 700 kg/m3,弹性模量E=69 GPa,屈服强度σy=76 MPa,泊松比μ=0.3。

选择参考文献[9]中两个球相互挤压变形的实验结果进行对比,证明采用的数值模拟计算方法是正确的。如图3所示,基于参考文献中的模型,数值模拟的计算结果和已有实验数据基本吻合。

P—外加压力荷载,N;δ—钢板的位移,m;M0—单位长度的塑性极限变矩,N。

2 分析和讨论

图4给出了金属空心球胞元的受力分析图。如图所示,当空心球发生塑性坍塌时,外力所做的塑性功为

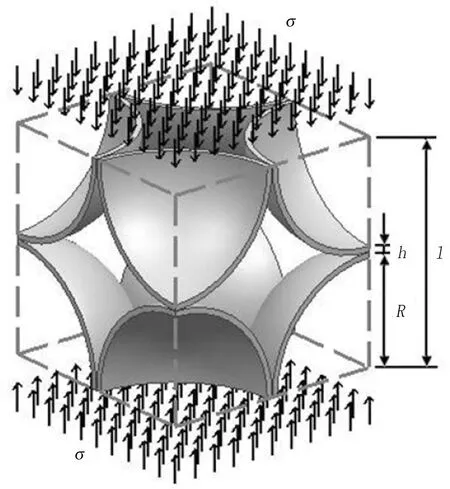
σ—名义应力,Pa;R—金属空心球的半径,m;h—金属空心球的壁厚,m;l—金属空心球的外直径,m。

2PRΦ=M0Φ

(2)

式中:R为金属空心球的半径,m;Φ为塑性铰发生塑性旋转的角度,rad。则金属空心球泡沫的平台应力如公式(3)所示。

(3)

图5给出了不同壁厚金属空心球泡沫的平台应力值。这里,平台应力为

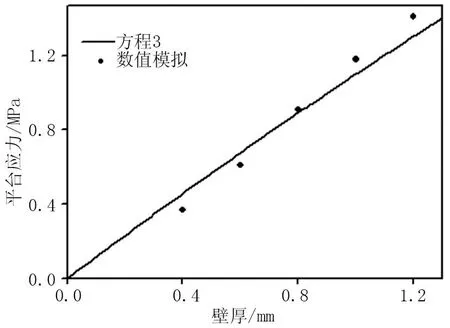
图5 不同壁厚金属空心球泡沫的平台应力值

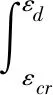
(4)

式中:ε为名义应变;σ为名义应力,Pa;εcr为与准静态塑性坍塌应力σcr所对应的名义应变值;εd为致密化应变。根据公式(3),图5同时给出了相应平台应力的理论预测值(图中实线)。如图所示,理论预测结果和数值模拟计算结果相互一致,这也进一步说明了数值模拟计算结果的正确性。

基于一维冲击波理论,Reid等[10-12]建立了均匀多孔材料的平台应力和冲击压缩速度间的关系表达式,即

σd=σcr+ρ*V2/εd

(5)

式中:ρ*为多孔材料的密度,kg/m3;V为冲击速度,m/s。这里将此公式推广到金属空心球泡沫。冲击条件下,金属空心球泡沫的动态平台应力为

(6)

根据公式(6),图6给出了不同冲击载荷作用下,金属空心球泡沫材料平台应力值的理论预测结果(图中实线)。此外,采用数值模拟的相应结果也在图6中给出。比较理论结果和数值计算结果,二者保持了良好的一致性。

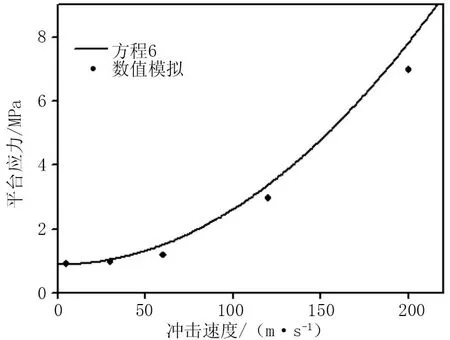
图6 不同冲击速度条件下简单立方排布均匀金属空心球泡沫的平台应力值(h=0.8 mm)

作为理想的能量吸收材料,载荷一致性是材料动力响应特性的重要评价指标之一。载荷一致性差不仅会影响材料的能量吸收能力,甚至可能会破坏材料失去基本的作用效果。载荷一致性可以通过两个参数表现,即最大应力值σmax和应力振动幅度σv[13],参数值越小说明材料的载荷一致性越好。这里取无量纲值进行分析,则

(7)

(8)

式中:ε0为初始应变;σp为平均名义应力,Pa。

图7给出了高速(v=200 m/s)冲击条件下,不同质量分布方式的金属空心球泡沫的平均名义应力、无量纲最大应力和无量纲应力振动幅度。为了对比分析,图中还同时给出了均匀金属空心球泡沫MBF的数值模拟计算结果。

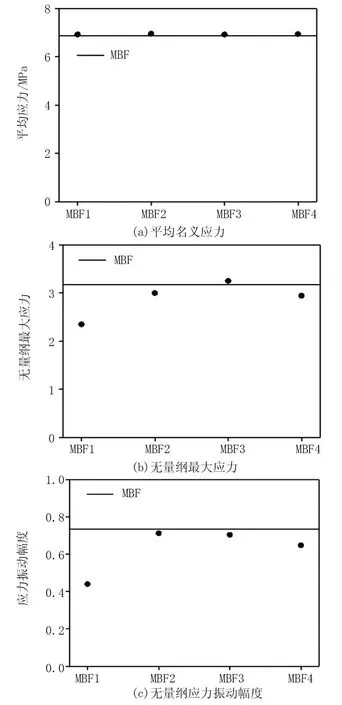
图7 高速冲击条件下金属空心球泡沫的动力学响应

如图7所示,在高速冲击条件下,均匀金属空心球泡沫和不同质量分布方式的金属空心球泡沫的平均名义应力值相近。这是由于在高速冲击条件下,泡沫材料的平均名义应力主要受冲击速度的影响。冲击速度相同,泡沫材料的平均名义应力相近。质量在空间分布对金属空心球泡沫的平均名义应力没有影响,但对金属空心球泡沫的载荷一致性有影响。从图中可以看到,金属空心球泡沫的无量纲最大应力和无量纲应力振动幅度结果基本保持一致。MBF1和MBF4排布方式的金属空心球泡沫表现出更优异的载荷一致性,超越了均匀金属空心球泡沫。MBF2和MBF3排布方式的金属空心球泡沫的载荷一致性和均匀金属空心球泡沫相近,没有明显的提高。这说明将质量在空间合理分布,即高密度质量和低密度质量交替排列分布的方式(MBF1和MBF4)不会影响金属空心球泡沫的基本力学性能,同时能够有效提高金属空心球泡沫的载荷一致性。

3 结 论

建立了金属空心球泡沫模型,研究了质量在空间的不同分布方式对金属空心球泡沫动力学响应的影响,重点讨论了冲击载荷作用下,不同密度金属空心球在空间的不同分布形式对金属空心球泡沫铝载荷一致性的影响。研究结果表明,将不同密度金属空心球在空间合理分布,即高密度质量和低密度质量交替排列分布的方式不会影响金属空心球泡沫的基本力学性能,同时能够有效提高金属空心球泡沫的载荷一致性。研究为开展泡沫材料的多目标设计提供了理论依据。