一“网”打尽——生态结构化教学新实践——以“圆的周长”的教学为例

江苏省南京市江宁实验小学 韩九洲

生态结构化教学的核心概念是“生态”与“结构”，这要求教师要着眼于知识的传授，课堂的价值要指向人的发展，二者在教学过程中相辅相成。教师应高瞻远瞩、提纲挈领，摒弃传统式接踵而至的设问、环环相扣的线性设计，立足教学过程结构化之上，不断优化符合学生认知特点、以生为本的网状教学设计。本文以“圆的周长”的教学为例，通过“织网”“撒网”“收网”“捋网”等措施，进行生态结构化教学新实践。

一、“织网”：察析生态特点，编织网状设计

“一位数学教师的职责是使学生了解数学并不是孤立的一门学问,而是一个有机的整体。”正如生态结构化教学的考量，以学习者为中心，以学生已有的知识为起点，先观察分析其思维发展，遵循生态性原则和过程性原则，把握好学生的认知结构，让发现式学习和开放式教学有确定的“度”，从而编织出一张新知识与各种形式有机结合的网。

师：老师寒假去游乐园玩，有两个摩天轮，票价一样，但老师喜欢追求刺激，你觉得老师会选哪一个？

（学生踊跃举手，争相发言）

生1：选周长更大的那个，待的时间更久、更刺激！

生2：选周长小的那个，转得快更刺激！

师：大家都提到了周长，这个摩天轮的周长在哪，谁上来指一指？

师：什么是圆的周长？

生：围成圆的曲线的长度是圆的周长。

师：圆的大小不同，周长也不一样，圆的周长可能与什么有关？同学们可以猜一猜。

师：同学们的想法很有价值，今天，我们就来探索圆的周长的奥秘。

（教师出示课题）

对于这一课程，教师在初次试上时利用轮胎引入课题，第二次试上时通过画圆引入课题，情境吸引力较弱，学生的反应比较沉闷，踊跃发言场面少见。因此，教师根据学生的特点及时调整为“追求刺激，二选一坐摩天轮”。学生的积极性被调动，无论是小摩天轮转得快还是大摩天轮在高处待得久，学生无一不提到了圆的周长。这既让学生在自然的生态中自由生长，又将本课的重心落在了圆的周长上。在学生进行小组交流、合作探究实验时，教师插入了一首钢琴曲作为背景音乐。钢琴曲是用圆周率π 谱写创作的，这也是数学与音乐结合的美。教师在进行整节课的网状设计时应做到纵观全课、高瞻远瞩，这正符合生态结构化教学所强调的，钻研教材时不仅要以教材的逻辑知识为起点，还要着眼于现实起点，对学生的认知起点、思维起点和情感起点进行洞察分析，从而更好地寻求书本知识与现实场景的切入点，将教材中呈现形式单一的静态资源转化为课堂所需的贴合生态的动态资源，织出一张富有弹性却不乏张力，学生能发现问题、探索问题、钻研问题的开放之网。

二、“撒网”：撒出生本之网，促进自由生长

就像卢梭认为儿童是自然的，应从人的自然本性出发进行自然的教育一样，生态结构化教学也要求赋予学生真正平等的权利。学生能够纯粹地发现问题、提出猜想、验证问题，最后得出结论。反之，有些教师授课时时常没有学生那么纯粹，他们总会从自己的视角预设，或者引导学生说出自己想要的答案，自认为能达成良好的课堂效果时，恰恰违背了以生为本的教学理念，掩盖了学生最朴素却又最有价值的想法，忽略了学生最原生态、最有想象力的思考，也大大降低了生生之间的群体认同。看似全课流畅、要点尽显，实则思维沉闷，学生陪教师演了一出自欺欺人的戏罢了。

师：圆的周长与直径间到底存在怎样的关系呢？同学们可以大胆地猜一猜。

生1：我觉得圆的周长可能是直径的2 倍。

师：你认为它们之间有倍数关系，且猜测是2 倍，很好，其他同学呢？

（教师板书：2？）

生2：我认为周长可能是直径的3 倍。

（教师板书：3？）

师：大家都猜测是倍数关系，那周长到底是直径的几倍呢？这个研究可有点难度，大家敢不敢挑战？

生（齐）：敢！

师：看在你们对数学钻研的这股劲儿上，老师给你们一些提示。

教师要敢于撒出“开放之网”“思维之网”“评价之网”。其实，学生的想法虽然朴素，但是充满张力，学生的潜力是无限的，他们的思维甚至如“大海”一般。教师还要敢于让学生畅所欲言，只要撒出那一张将全班学生紧紧凝聚在一起的“以生为本”的网，去唤醒、去激活、去放大、去捕捉，就能促进学生对深层资源的群体认同和理解。

师：怎样测量圆的周长呢？老师这就有一个圆，谁来说说怎么测？

生1：用一根线绕圆一周，然后把线拉直用直尺量。

（学生上台演示）

师：这个方法可行吗？给他热烈的掌声。这在数学上叫作“绕线法”。

生2：我觉得可以在圆的一圈涂上颜料，在纸上滚一圈再用直尺量颜料的痕迹。

师：你很有想象力，这方法是可行的！能不能利用我们现有的工具？（先肯定，再捕捉并激活）

生3：我觉得可以直接让圆在直尺上滚，为了方便判断是否转了一圈可以先在圆上做一个记号。

（学生上台演示）

师：此处应该有掌声。在数学上叫作“滚轮法”。

师：无论是“绕线法”还是“滚轮法”，在操作过程中有没有共同之处？

（教师放大、激活：演示将线由曲拉直的动作）

生4：它们都将曲线转化为直线。

师：真有数学的眼光和思维！在数学上，这种思想就叫作“化曲为直”。

生态结构化教学理念不是“只走华山一条路”，而是“条条大路通罗马”，看似“巧妙”的线性设计只会束缚学生的“灵光一现”和“拨开云雾”。怎样测量圆的周长？很多学生能想到用线绕一圈拉直了量，第一个学生上台展示是对台下的同学的第一次启发。很快，有的学生想到用颜料将圆的周长在纸上表示出来（学生真实的生成展现了思维的逐步进阶），这是对台下的同学的第二次启发。最后，有的学生凝练出“滚轮法”。在生生互动中，那些有着“宽厚知识储备”的学生也在引领着其他学生进阶，群体的认同感油然而生，这就是学生的创造！当教师做好引领，真正放手将课堂交给学生时，也许学生还给教师的不再是当时的那颗种子，也许是参天大树，也许是整片森林。

三、“收网”：百家争鸣寻真理，网罗万象促深思

学生经历了原生态的思考后产生了本真的认识与理解。这些认识与理解虽然是学生自己独立思考后的雏形，却有着强大的生命力；虽然是最自然、最饱含局限性的朴素理解，却富有个性和创新性，这是寻求新知、思维进阶的起点。教师在“收网”时，要网罗万象，关注学生的思考，引领学生从朴素的思考走向精练，梳理学生的自然感悟，这样才能探索出规律，推广出价值，增添思想的普遍性，实现群体的认同。

在教师提出“圆的周长到底是直径的几倍”后，学生内心已有一定的想法。此时，教师给予学生两个提示，引导学生任选其一，并在小组内交流想法。在分享环节，学生大胆上台说自己的想法，首先自己要说清楚、讲明白；台下学生仔细倾听，能够复述、补充或质疑，做到能甄别、能比较；全体参与，将“个人经验”传递给每一个学生，从而促成群体认同。

师：（出示图1）两个提示任选其一，谈谈你有什么发现？有想法了就小组交流分享一下。

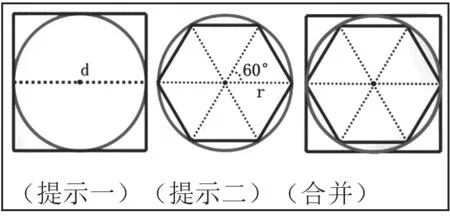
图1

（学生充分交流，并上台分享）

生1：我发现圆的直径与正方形边长相同，正方形的周长就是4d，圆的周长比正方形的周长小，所以c＜4d。

生2：我发现这是等边三角形，所以正六边形的边长就是r，周长就是6r，也是3d，圆的周长比正六边形要大，所以c＞3d。

师：我把两个同学说的合在一起，那么，圆的周长应该？

生（齐）：大于3d小于4d。

师：就在今天，我们班的同学提出了一个重大发现，他们认为圆的周长是直径的3 倍到4 倍。在数学上，提出一个问题往往比解决一个问题更重要，我建议全班同学给他们以热烈的掌声！

在学生上台分享的过程中，教师应注意台上同学与台下同学关系的联结。学生作为课堂的主体，应由他们自己去发现、创造，学生已有的知识、经验、技能足以支撑他们从具体形象的图形中抽象并提炼出关系。学生拥有雄厚的基础，只要有一个平台，就能自由交流、自然生长；教师“张网收鱼”，引领好方向，纲举目张之后就能收获一网活泼之“鱼”，一网形态各异之“鱼”。

师：（出示图2）观察三个同学手上的圆与算出的数据，结合我们的猜想，你有什么发现？

图2

（巨大的圆与硬币形成鲜明对比，视觉的冲击激活了每个学生的思维）

生1：我发现虽然大小不同，但是，它们周长除以直径的商都在3 和4 之间。

生2：跟我们猜想的一样，圆的周长总是直径的3倍多一些。

师：再观察后面两组数据，还有什么想说的？

生：两个圆直径相同，周长却不同，说明测量时存在误差。

师：咱们来看看数学家们精准的测量。同学们计算的结果跟数学家计算的结果非常接近，但数学家们还做了一件事，请仔细看好。（几何画板中演示圆不断变大）你们有什么发现？

生：我发现圆的周长在变，直径在变，周长除以直径的商却一直固定不变。

师：数学家把这个不变的量命名为圆周率，用字母表示就是π，你们觉得π 是一个怎样的数？

生3：π 虽然是一个字母却表示一个固定的数。

生4：我补充，这个数还是一个无限不循环小数。

每个学生都是一个独立的个体，在巨大的圆与硬币强烈的视觉冲击下，每个学生都用自己的方式思考着。教师抛出问题提纲挈领之时，亦是学生思维沸腾喷涌之时。学生在惊叹之余分享着自己的感受，相互补充、相互影响、相互沟通，探索得愈发深入，对“圆的周长总是直径的3 倍多一些”的理解也愈发深刻。课堂上的每一个生态要素都在引领下不断优化组合，每一个学生的思维都在不断地成长，“收网”之余呈现出一定的张力。

四、“捋网”：捋清探究过程，凸显结构理念

本课共有两次回顾，第一次回顾在探究出圆的周长公式后，教师提问：“回顾整个过程，我们是怎样一步一步发现并探索出圆的周长与直径之间的关系的？”学生通过独立回顾，感受到经历了观察、猜想、验证、推导公式等过程，一个公式的得出不是简单地了解及记忆，而是要通过不断地钻研，亲自动手开展数学实验，在想象、思考、质疑、领悟中推理出新知。第二次回顾，教师先与学生分享了数学史料。从 “周三径一有余”到 “割圆术”,再到祖冲之的精确到小数点后七位的圆周率，学生深刻体会到我国数学家们不畏艰苦、不断超越的精神，民族自豪感油然而生。接着，教师引领学生回顾正方形周长与边长的关系，等边三角形周长与边长的关系及今天刚学习的圆的周长与直径的关系，唤醒学生的旧知，激活其对平面图形周长与边长或直径之间关系的整体感知。数学是一门严谨的学科，数学知识也具有高度的抽象性和应用性。教师不仅要传授知识，还要向学生传递思想，做到导之有度，让学生悟而有助。

教学在练习部分设计了三个小游戏：“争分夺秒”抢答题、“神机妙算”计算题、“我写你猜”物体周长感知题。“人是环境中的人”，数学源自生活，自然用于生活。在“争分夺秒”中，学生玩得不亦乐乎，巩固了圆的周长公式，还学会了用含有π的式子表示周长；在“神机妙算”中，学生情不自禁地感叹圆周率的好处；在“我写你猜”中，学生利用估算得出直径，根据已有的生活经验猜出直径约为2.5 cm 的物体是一枚硬币。公布答案时猜对的学生神采飞扬，这不正是生态结构化教学所追寻的画面吗？

生态结构化教学传递的是开放、动态的课堂教学，教师将全课的核心问题编织进一个网中，创设一个自然、生态的情境，发掘出藏匿于学生思维深处的核心问题，在自由平等的平台上，生生互动，让数学课堂充满活力。学生如鱼儿般在思维的海洋里徜徉，自由探索，发现疑点、生成困惑。教师只需收紧绳线，将它们一“网”打尽，就必然呈现出一幅精彩绝伦的画面。