删繁就简三秋树,领异标新二月花
2024-05-14王浩宇
王浩宇

摘要:分析2023年数学新高考Ⅰ卷,发现题型和难度相对稳定.新高考试题简洁明了,考查学生基础知识的同时重视学生关键能力的探求.本文中通过整体试卷评析、部分试题评析及近三年全国卷对比评析三个板块对2023年新高考Ⅰ卷进行评价.
关键词:新高考Ⅰ卷;试题分析;试卷评析
1 综述
2023年教学新高考Ⅰ卷严格依据高中课程和高中课程评价体系,深化基础性和综合性,注重数学运算[1].试题简洁明了,体现数学的简洁美,考查基础知识的同时重视学生关键能力的探求,传承经典的同时又体现了对考生的人文关怀,开拓创新,服务于高校人才选拔.
2 整体试卷评析
2.1 难度适中,梯度设置合理
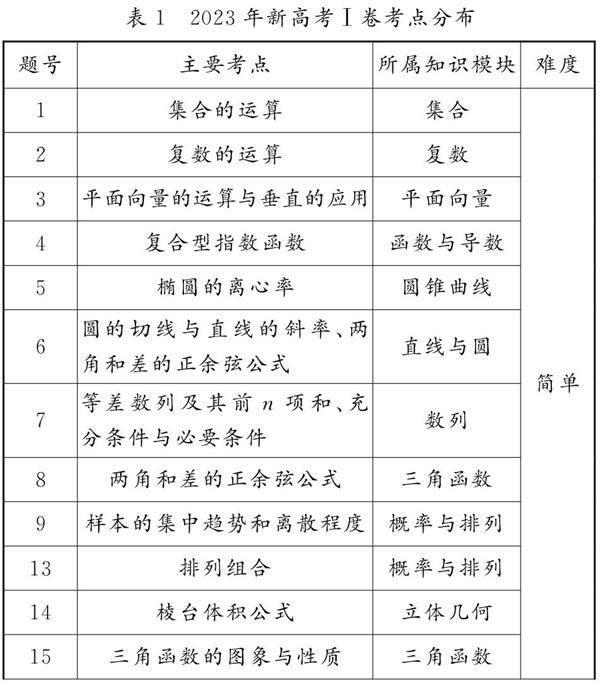
今年新高考Ⅰ卷整体难度与去年基本持平,试题着力于通性通法和综合能力的考查.具体考点分布情况如表1:
试卷简单题共60分,体现新高考Ⅰ卷植根教材、重视基础、启发课堂德育的理念.对比去年试题,选择题难度略降,填空题难度相当;中等难度题有一定计算量,需要综合运用所学知识求解;层次高的难题,大约占29分,试题重视思维的创新和学生的综合能力,考查逻辑推理、数据分析、数学运算等核心素养.
2.2 层次分明,突出重点内容
2023年新高考Ⅰ卷在多方面体现重点内容重点考,具体内容如图2所示:
相比浙江卷,新高考Ⅰ卷增加了多选题,丰富题目类型的同时注重知识点的覆盖,突出主干知识.其中函数与导数、概率、立体几何、圆锥曲线考题较多,集合、复数、直线与圆、平面向量更多体现工具性.同时,今年客观题难度整体降低,中低档试题数量增加,旨在减少学生“放题”的情况.
2.3 反对套路,注重全面发展
新高考Ⅰ卷未划定试卷结构,例如今年导数位于第三题.解答题从第二小题开始,每题均能多解,这是新高考在引导学生做“六边形战士”.以解三角形为例,今年考查求三角形的高,相比去年考查正弦定理、余弦定理与两角和差的正余弦公式,三角形高的求解更能展现学生对三角形本质的理解,体现了新高考的反套路.
新高考还在选择题中反套路,每年选择题答案中ABCD数量都不同,加大了考生猜题的难度.
2.4 追根溯源,回归书本题源
2023年新高考Ⅰ卷选择题起点较低,许多题目源自书本.虽然试题来源于课本,但又高于课本,简单的题目中也有“绕弯”的内容.具体内容如表2:
例如试卷第7题,以选择性必修二人教A版课后习题第7题第一小题为题源,借助充分条件与必要条件的工具性,考查学生对数列定性分析的掌握情况,以概念、定理、试题为命题的起点,注重“四基”的考查.2021年全国甲卷第7题也属于类似题目.上述题目让学生感悟定性分析的同时培育了逻辑推理的数学能力,体现了数学的育人价值.
[HJ1.35mm]
2.5 简洁明了,彰显数学之美
希尔伯特在《数学问题》中曾说过:“一个数学理论,只有当你能把它向你在街上遇到的第一人阐述得很清楚时,它才算完整.”新高考Ⅰ卷在各个方面均体现了简洁美.具体内容如图3:
此类题目共计32分,说明依赖题海在高考中并不是有效的.知识的综合让题目思维量更大,考查学生是否真正掌握了相关概念.
3 部分经典题型与创新题型评析
3.1 讲究算理,计算需谨慎
运算是高考重点考查内容之一,主要分为运算规则、运算律、运算方法的考查.
第10题属于应用题,主要考查学生对对数和不等式运算性质的熟练程度.
(2023年新高考Ⅰ卷·10)噪声污染问题越来越受到重视.用声压级来度量声音的强弱,定义声压级Lp=20×lgpp0,其中常数p0(p0>0)是听觉下限阈值,p是实际声压.下表4为不同声源的声压级:
评析:本题以时事热点新能源汽车为背景,设置科学研究情境,体现数学的生活性.此类问题求解时要牢牢抓住中间量,将其余变量用中间量来表示.相比前几年的比大小试题,结合实际情境更能培养学生阅读能力和数学算理.
评析:掌握运算规则可以拓宽解题思路.以第11题抽象函数为例,基本策略是根据抽象函数的结构构造函数求解.基于g(xy)=g(x)+g(y)中乘法变加法的运算规则,以对数函数为基础构造函数求解.常见的运算规则还有指数幂运算规则、三角函数运算规则等.
〔2023年新高考Ⅰ卷·20(2)〕设等差数列{an}的公差为d,且d>1.令bn=n2+nan,记Sn,Tn分别为数列{an},{bn}的前n项和.
若{bn}为等差数列,且S99-T99=99,求d.
评析:合适的运算方法可以让解题思路更清晰.例如数列第二小题以常规方法求解对思维含量要求较高,若以b1,b2,b3间的关系求解能最快得出结果,体现运算方法选择的重要性.
历年高考计算都是重中之重,以考促教,为教师教学提供方向.此题对深谙算理的考生不成问题,但对不够细心认真的学生则是一个“暗点”,考查了学生数学运算等核心素养.如果学生心理素质较好,能够合理选择算法此题甚至能成为简单题,这也说明平时培养学生算理的重要性[2].
3.2 结合模型,初判對与错
(2023年新高考Ⅰ卷·12)下列物体中,能够被整体放入棱长为1(单位:m)的正方体容器(容器壁厚度忽略不计)内的有( ).
A.直径为0.99 m的球体
B.所有棱长均为1.4 m的四面体
C.底面直径为0.01 m,高为1.8 m的圆柱
D.底面直径为1.2 m,高为0.01 m的圆柱体
评析:立体几何的接切问题一般考查外接球和内切球,但本题考查正方体的接切问题,四个选项难度逐渐增加,分别考查球、正四面体、圆柱三种空间几何体,考查范围更广,更能表现考生思维的灵活性与创造性.
此类题目解题步骤为:套用已知模型→比较已知模型与选项差异→极限法求解问题.解题时,需要学生充分发挥空间想象能力.基于此,在教学过程中,教师可以结合书本和课标中的立体几何模型授课,帮助学生熟悉常见模型的同时培养学生空间想象能力.
3.3 阅读分析,课外需拓展
(2023年新高考Ⅰ卷·21)甲、乙两人投篮,每次由其中一人投篮,规则如下:若命中则此人继续投篮,若末命中则换为对方投篮.无论之前投篮情况如何,甲每次投篮的命中率均為0.6,乙每次投篮的命中率均为0.8.由抽签确定第1次投篮的人选,第1次投篮的人是甲、乙的概率各为0.5.
(1)求第2次投篮的人是乙的概率;
(2)求第i次投篮的人是甲的概率;
(3)已知:若随机变量Xi服从两点分布,且P(Xi=1)=1-P(Xi=0)=qi,i=1,2,……,n,则E(∑ni=1Xi)=∑ni=1qi.记前n次(即从第1次到第n次投篮)中甲投篮的次数为Y,求E(Y).
评析:第21题第(1)问以选择性必修三(人教A版)7.1.2中的思考题为题源,考查全概率公式,求解时需要仔细读题,分清主从关系,借助对应模型求解.
第(2)(3)问则以选择性必修三课后复习参考题第10题(第91页)为题源,考查学生对概率与数列的掌握情况与获取信息的能力,把问题转化为数列模型.以前应用类考题以函数与方程为主,本题则以马尔科夫链为背景,取材于学生熟悉的情境,考查学生多知识综合运用的能力,为大学学习做铺垫,发挥高考的选拔功能.相比传统的概率考题卡方检验、线性回归等,基于统计模型的试题更为灵活.相关模型还有决策树、朴素贝叶斯、逻辑回归、线性回归等,可以作为出题的参考内容.此类题目在2019年全国乙卷中也曾出现过.
3.4 模式改变,不变应万变
(2023年新高考Ⅰ卷·22)在直角坐标系xOy中,点P到x轴的距离等于点P到点0,12的距离,记动点P的轨迹为W.
(1)求W的方程;
(2)已知矩形ABCD有三个顶点在W上,证明:矩形ABCD的周长大于33.
评析:与前几年导数压轴题不同,今年的压轴题是解析几何,题目由易到难,第(1)小题入口较宽,根据题意列式求解即可.但学生面对压轴题时,常常会产生畏惧心理,导致失分.这需要教师在平时多鼓励学生勤于思考、勇于探索,不能看到压轴题就畏难、放弃,体现了命题人的良苦用心和数学的育人价值观.
第(2)小题较为复杂,是拉开学生分数差距的点.本小题可以从矩形的邻边垂直切入,通过设点或设线求解问题.但不管用哪种方法,都需要回归直线的斜率,让问题变得更直观,这是本题设计的亮点.题目本身并不复杂,条件清晰,解题时学生能轻松想到两点之间的距离公式(x1-x2)2+(y1-y2)2以及弦长公式1+k2\5|x1-x2|,但计算仍是学生的痛点,需要选择合适的算理.本题主要考查数学运算、逻辑推理等核心素养,同时对学生的心理素质、应变能力提出了一定的要求.
解析几何大题对广大考生来说是一个挑战,要求学生对通性通法能熟练应用的同时,还需思维灵活、注重算理,属于层次较高的难题.因此在复习中要引导学生合理猜想,结合算理发掘关键点,突破关键,计算到底,从而提升数学综合能力与核心素养,尽力做到难题多拿分,简单题不失分.
4 总结:灵活考查,复习需要方向.
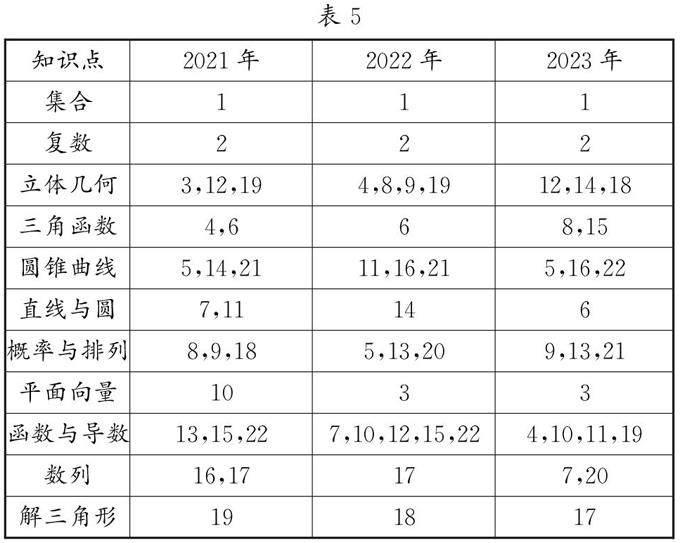
2023年新高考Ⅰ卷为后续高考提供了复习方向与教学思路,虽然每年考题难度、位置分布不同,但作为浙江参与新高考的第一年,题型改变仍有一定规律,以下(表5)是2021年-2023年新高考Ⅰ卷考查的知识点位置分布情况.
历年高考试卷中有变与不变两部分.其中,①函数与导数、立体几何、圆锥曲线、概率与排列每年均有大量题目,难度跨度较大;②平面向量、直线与圆、解三角形、数列部分题号虽有变动,但难度适中,题量仅有1到2题;③集合与复数等基础考点的题号、难度3年内均未改动;④函数、向量、几何、统计、概率、数列、不等式仍是高考的重点与难点.解题时,考生需要把握常用逻辑用语、集合、不等式、函数与导数的工具性,多角度思考问题.
新高考Ⅰ卷另一特点是中档题多,这为高考复习提供了方向:普通考生需注意在集合、复数、平面向量等简单题上不丢分,在直线与圆、三角函数、解三角形、立体几何、数列等中档题上多拿分.想拿高分的考生也需注意,虽然考查的知识难度年年发生变化,但不存在遗漏的考点,这是高考在传达“不放弃任意一个知识点”的观念.
对比2021年-2023年新高考试题发现:数列大题在2021年难度较大,但2022和2023年处于中档难度.2023年三角函数大题的难度有一定提高,函数与导数的难度有所降低.近几年新高考小题中都出现了与导数相关的题目,旨在打破传统印象中导数均是难题的观念,立足计算,考查导数的工具性,后续是否继续降低难度仍需观察.另外,每年新高考都在应用题中进行创新,其中2023年新高考Ⅰ卷应用题具体内容如表6所示.
在命题原则上,新高考Ⅰ卷注重以下三点:
(1)跳出框架.新高考并不存在固定题型,规避题型模式化和解题模式化,但也提供了复习的方向和策略.在此对2024年新高考压轴题进行预测:能作为压轴题出现的往往有数列、导数、解析几何,新高考以数列压轴的可能性较低,2023年是圆锥曲线压轴,故考虑2024年有可能回归导数压轴,考法可能会参照2023年,结合高等数学中的重要结论呈现问题会更简洁.
(2)注重计算.新高考题目计算量很大,故需要注重算理,掌握算法,计算到底.
(3)注重应用.新高考题目往往结合其他知识或加入实际情境,对基础知识进行深化,将题目改编成需要“绕弯”的难题.考试时,虽然题目给学生似曾相识的感觉,但拿满分往往较困难.
综合命题原则与新高考试题特点,总结出以下三点教学启发:
(1)基于课标,牢固掌握知识
课标是出题的依据,教学时基于课标设计教学内容,让学生完全掌握相关概念,回归课本,讲解通性通法,减少“二级结论”.
(2)侧重算理,掌握做题技巧
新高考Ⅰ卷的计算量较大,因为计算失分较为可惜,因此,平时要让学生自己动手运算,合理简化运算,减少运算量,培养学生的运算能力,同时培养学生运用排除法、特殊值法等运算技巧解题的能力,提高做题效率.
(3)综合应用,参考课标实践活动
新高考Ⅰ卷的难题会综合考查多种知识点,在平时教学过程中,可以通过实践活动帮助学生完成知识的整合,避免知识的碎片化.
参考文献:
[1]中华人民共和国教育部.普通高中数学课程标准(2017年版)[S].北京:人民教育出版社, 2018:1-2.
[2]陈宏.基础与能力并重 经典与创新共存——2022年浙江省高考数学试题评析[J].中学数学,2022(19):27-32.
