导学互动模式在高中数学教学中的应用

范仁忠

在新课改的背景之下，极具高效性和科学性的高中数学导学互动教学模式正在被广泛运用.该模式是一种以学生为主体，教师与学生之间进行互动合作的教学方式[1].在该模式下，教师的角色发生了极大的改变，他们不再是知识的构筑师，而是承担起了引导的职责，通过设疑提问、引导讨论、合作探究等方式，培养学生的学习能力，让学生自主完成知识的构筑过程.

1 导学互动模式的应用原则

1.1 提高学生主动参与性

导学互动模式的核心是激发学生的主动参与，教师应通过设计问题、引导讨论和组织合作等方式，激发学生的兴趣和积极性，使他们主动参与到学习中.教师可以采用开放性问题和启发性问题，让学生走出思维的舒适区，拓展他们的思维边界.在教师的引导下，学生可以主动联系所学，认知到问题的本质，完成自我意识下的思考以及探究过程，成为学习的主人，实现深度学习.

1.2 引导学生自主探究

导学互动模式强调的是学生自主寻找解决问题的方法和破解策略，注重的是将学生从被动接受知识的角色转变为主动参与者和探究者.教师在教学过程中应给予学生一定的自主空间，让他们自己主动思考、尝试和解决问题，通过自主探究的过程，加深对知识的理解和应用.

1.3 促进学生思维能力的培养

导学互动模式旨在培养学生的思维能力，教师

在教学过程中，可以通过问题链、思维导图、开放性试题、知识辩论等方式，让学生的分析、推理等思维全面开花.例如在思维导图制作环节，教师可以让学生分析和整理

一个主题或概念，并用框图的方式呈现出来，从而培养学生的归纳和概括能力.

2 导学互动模式的应用例析

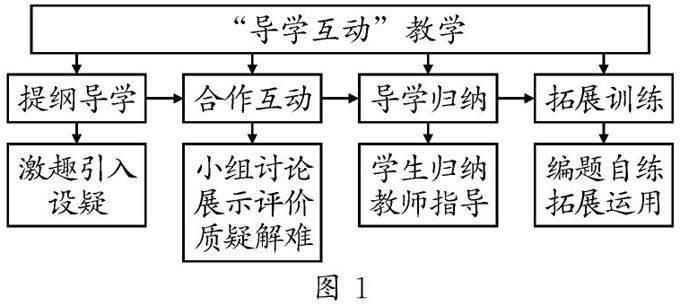
导学互动教学的基本模式结构图如图1所示.

下面以“指数函数”为例，探讨如何在教学过程中实施导学互动模式.

2.1 提供导学提纲，明确教学目标

导学互动教学模式的第一个环节，就是为学生提供课前导学提纲.通过这些提纲，学生可以对知识进行预了解，从而提高课堂效率.“指数函数”的导学提纲中教学目标如下所示.

教学目标：

（1）知识目标：了解指数函数的概念，并能够掌握指数函数的图象和性质；

（2）素养目标：能够通过情境引入中的指数函数，分析归纳出指数函数的表达式，并能够通过指数函数模型比较两个幂值的大小；

（3）能力目标：能够灵活运用数形结合思想分析、解决实际问题.

教学重点：了解指数函数的概念，并能够掌握指数函数的图象和性质.

教学难点：灵活运用指数函数的图象和性质解决实际问题.

设计意图：给学生提供导学提纲的目的是为了培养学生的自主学习能力和探究精神.教师通过设定明确的学习目标和指导方法，引导学生主动参与学习过程，自主探索数学知识.建構主义观念认为，“学生不是空着脑袋进入教室的”，这意味着学生具有自己的经验、知识和思考，教师可以借助这些已有的认知基础引导学生学习新知识[2].特别是对于高中生来说，数学知识晦涩难懂，如果没有提前预习，学习新课时会较为困难.

2.2 创设情境，激趣引入

在课堂开始时，教师可以利用生活情境或真实案例引入课堂内容.这样可以激发学生的学习兴趣和好奇心，并帮助他们将所学内容与实际生活联系起来.

师：数学是源于生活，又服务于生活.当我们思考或求解某一个问题时，数学就是我们的工具.《庄子＼5天下》有一个实际的生活问题，大家尝试下，看能否从数的视域对其进行解释？

（课件展示.）

师：这个式子是函数吗？理由是什么？

生：是函数，因为对每一个确定的x的值，都有唯一确定的y值与之对应.

师：这个函数的y值一定大于0吗？

生：是.因为（1/2）x代表的是x个1/2]相乘，其值一定大于0.

师：“万世不竭”，我们刚刚从数的角度，对木棒的该现象进行了解释.

师：假设现在将函数的定义域拓展为整个实数集，大家觉着会发生什么变化呢？y=（1/2）x还是函数吗？

设计意图：“生活即教育”，这句话强调了教育不仅仅发生在教室里，而是贯穿于我们的日常生活中，二者不可分割，相互联结[3].导学在于“以导促思”，而这个“导”，关键在于寻找与学生生活经验和教学知识的联系.学生的生活经验和认知是他们思维的基础，是他们对世界的观察和理解的来源.因此，教师在导学时，应该充分了解学生的生活经验和认知水平，并将这些作为教学的依据.建立起经验认知和所学知识的桥梁，学生可以更为快速、高效地掌握和理解新学知识，从而提高课堂效率.

2.3 合作互动，探索新知

（学生自学教程，回答问题.）

生：当我们把定义域扩展至实数集时，y=（1/2）x

仍然是函数.

师：这种函数有什么特征？

生：底数是常数，指数是自变量x .

师：形如y =ax（a>0，a≠1，x∈[WTHZ]R[WTBX]）的函数，就是我们今天要研究的指数函数.

师：接下来请大家以小组的形式，回顾我们已经学过的二次函数图象和性质的研究方法，采用类比的方法研究指数函数.

活动1：填表并画出函数y=12x的图象.

活动2：在同一坐标系中分别画出函数y=（1/2）x和y=2x的图象.

师：通过上面的活动，大家发现了指数函数的什么性质呢？

（学生交流讨论，回答问题.教师修改补充，展示最终答案.）

设计意图：在导学互动模式中，合作学习是重要的组成部分.教师在运用导学互动模式教学时，应该注重学生自主思考与小组集体合作的巧妙结合.教师的任务是辅助学生学习，通过提供合适的学习资源、指导正确的学习方法、设置梯度式的学习任务等方式，引导学生顺利完成自主学习.同时，在自主学习的过程中，教师可以组织学生进行小组讨论，以促进学生间的交流合作，发展学生团队分工协助的能力.

2.4 自主概括，内化新知

让学生从知识层面、思想层面以及核心素养培养层面对本节课进行归纳总结.

师：在本节课上，我们习得了哪些知识？用到了哪些数学思想方法？本节课对我们核心素养的发展有何作用？

（学生总结归纳，教师补充.）

2.5 结合个体，当堂自测

根据学生的能力水平，调整训练内容的难度，确保每个学生都能够在适当的水平上进行训练.

从求解函数解析式、构造指数函数、函数性质的应用等方面，设置不同层次的题型进行当堂训练.

学生自主答题，教师根据学生学习情况进行适当的指导和讲解.

设计意图：导学互动模式虽然是集体式课堂，但也应该兼顾学生的个性化发展.每个学生都是独特的个体，他们的学习需求和发展路径也有所不同，教学中需要根据学生的能力水平确定训练内容的难易度.有些学生可能已经掌握了基本知识，需要更高层次的挑战，而有些学生可能还需要巩固基础知识.因此，在进行当堂训练时，应设置基础、拔高以及延伸拓展等不同的难度等级，不能均为简单或者复杂，题目设置一定要有梯度.同时，教师要及时提供反馈和指导，让学生认知到自己的错误，在纠错的过程中，进一步加深对知识的掌握程度.及时的反馈，可以让学生对自己的学习情况有一个了解，进而调整与自身状况不匹配的学习策略.此外，教师的指导也可以帮助学生更好地理解知识，提高学习效果.

在导学互动模式下，教师可以根据不同的教学内容和学生的实际情况来灵活运用导学互动模式.随着科技的不断发展，教育技术的应用也越来越广泛，导学互动模式可以结合教育技术的优势，创造更多的互动形式，提供更丰富的学习资源，进一步提升教学效果.此外，导学互动模式也可以与其他教学模式相结合，形成更完整的教学体系，促进学生的全面发展.