重视概念教学 提升核心素养

杜文伟

摘要：本文中基于《普通高中数学课程标准（2017年版）》中阐述的在学生学习数学和应用数学的过程中，学生能发展数学抽象、逻辑推理、数学建模、直观想象、数学运算、数据分析等数学学科核心素养，以人教A版选择性必修第一册“2.1倾斜角和斜率”概念课为例进行教学设计.数学概念是数学的灵魂，概念教学一是要抓住概念的“质”（概念的内涵），二是要抓住概念的“量”（概念的外延），在此基础上培养学生的核心素养.

关键词：直线；倾斜角；斜率

本节主要是结合问题导向，让学生探索在平面直角坐标系中确定一条直线位置的几何要素，从而得到直线的倾斜角、斜率的概念及斜率公式等，让学生经历用几何和代数的不同思想在平面直角坐标系中定量刻画一条直线位置的过程，感悟平面解析几何中蕴含的数学思想.

1 教学分析［1］

1.1 教材分析

本节是平面解析几何的起始课，将采用坐标法研究平面几何图形问题.直线的倾斜角和斜率是刻画直线倾斜程度的几何要素与代数表示，是学习平面解析几何的基础.在直线与直线，直线与圆、椭圆、双曲线和抛物线的位置关系以及其他相关综合问题的解决上，直线的斜率都会起到非常重要的作用.通过本节的学习，学生能够体会平面解析几何中蕴含的数学思想，进而能够提升数学核心素养.

1.2 教学目标

1.2.1 知识与能力目标

（1）理解与掌握直线的倾斜角和斜率的概念，掌握直线斜率的计算公式，理解直线的方向向量与斜率的关系；

（2）培养数学抽象思维、问题探究等基本的数学思维能力；

（3）能够利用数学知识解决简单的实际问题；

（4）通过知识学习，体会分析与解决问题的数学思想和方法.

1.2.2 學科素养目标

（1）经历从数量关系和图形关系中抽象出直线斜率概念的过程，提升数学抽象核心素养；

（2）利用图形描述，建立倾斜角和斜率即数与形的关系，提升直观想象核心素养；

（3）通过依据三角函数运算法则求得运算结果，提升数学运算核心素养.

1.2.3 情感态度价值观目标

（1）通过数学学习活动，体会数学的特点，培养数学的思维品质；

（2）培养独立思考、合作交流、严谨求实的科学态度和对知识探究的理性精神.

1.3 教学重难点

教学重点：直线的倾斜角和斜率的概念、斜率公式.

教学难点：直线的斜率和倾斜角之间的关系.

2 教学过程

探究1：确定直线位置的几何要素（点和方向）.

问题1 一次函数与直线是否一一对应？

学生：一次函数的图象都是直线，反之不一定，故一次函数与直线不是一一对应.

问题2 对于平面直角坐标系中的一条直线l，按照教材中定义的直线的方向，如何利用平面直角坐标系确定它的位置？

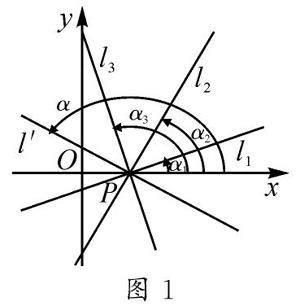
观察图1，你能说出这些直线的区别吗？

学生甲：这些直线相对于x轴的倾斜程度不同.

学生乙：这些直线与x轴所成的角不同.

追问：如何用直线与x轴所成的角来表示这些直线的方向或倾斜程度呢？

学生：需要定义直线与x轴所成的角.

教师：很好，下面我们进入下一个探究.

设计意图：通过问题导向，引入直线的倾斜角这一重要概念，培养通过图形关系抽象数学概念的数学抽象核心素养.

探究2：利用直线的倾斜角定量刻画直线的方向.

教师：直线倾斜角的概念（略）.

学生小组合作学习1：

根据教材中定义的直线l的倾斜角的概念，我们知道直线l的倾斜角α的取值范围为00≤α<180°，那么如何理解直线的倾斜角呢？

学生探究，教师总结：

（1）直线的倾斜角可以定量刻画平面直角坐标系中一条直线的倾斜程度，是从“形”的角度定量刻画直线相对于x轴正向的倾斜程度；

（2）从运动变化的观点看，当直线与x轴相交时，直线的倾斜角可以理解为由x轴绕着直线与x轴的交点按逆时针方向旋转到与直线重合时所旋转的最小正角.

设计意图：使学生理解在平面直角坐标系中确定直线位置的几何要素是直线上的一个点和倾斜角，从而借助图形培养学生直观想象核心素养.

追问：你能在表1中准确画出下列直线吗？

例1 （1）图2中直线l的倾斜角为[CD#3].

（2）若直线l向上的方向与y轴的正方向成30°角，则此直线的倾斜角为[CD#3].

问题导向：通过以上学习，我们可以理解直线的倾斜角是从“形”的角度量化直线相对于x轴正向的倾斜程度，那么是否也可以从“数”的角度来量化直线的倾斜程度呢？

探究3：用直线的斜率量化直线的倾斜程度.

问题3 直线l的倾斜角α与直线l上P1，P2两点的坐标有什么关系？

学生小组合作学习2：

在平面直角坐标系中，设直线l的倾斜角为α，分别讨论当直线l满足下列情况时，直线l的倾斜角α与此直线上两点坐标的关系：

（1）已知直线l经过两点O（0，0），P（3，1）；

（2）已知直线l经过两点P1（－1，1），P2（2，0）；

（3）已知直线l经过两点P1（x1，y1），P2（x2，y2）（x1≠x2）.

[JP5]教师总结：直线l的倾斜角α与P1（x1，y1），P2（x2，y2）（x1≠x2）

两点坐标的关系为tan α=y1－y2x1－x2=y2－y1x2－x1.

问题4 当直线P1P2与x轴平行或重合时，上述

式子还成立吗？

学生：成立.因为当直线P1P2与x轴平行或重合

时α=0°，

则tan α=tan 0°=0.又P1（x1，y1），P2（x2，y2），

x1≠x2，y1=y2，则

y2－y1x2－x1=0.所以tan α=y2－y1x2－x1.

引入斜率的定义：我们把直线l的倾斜角α的正切值叫做这条直线的斜率，即斜率k=tan α（α≠90°）.

学生小组合作学习3：

通过上述探究我们知道，当直线l的倾斜角α不为90°时，其斜率是一个实数，如何理解其斜率呢？

（1）可以用斜率这一实数量化倾斜角不是90°的直线相对于x轴正向的倾斜程度；

（2）直线的倾斜角和斜率都是刻画直线相对于x轴正向的倾斜程度的，倾斜角侧重于从几何角度而斜率侧重于从代数角度刻画.

思考：为什么用倾斜角α的正切值定义直线的斜率，而不是用倾斜角α的正弦值或余弦值呢？

学生讨论，教师总结：

（1）在后面直线方程的学习中，直线方程中x，y的系数反映了直线倾斜角的正切值;

（2）数学来源于生活又服务于生活，我们日常生活中常用“坡度”表示一倾斜面的倾斜程度，坡度=铅直高度水平宽度，此计算公式体现的正是倾斜角的正切值.

学生小组合作学习4：

问题5 直线l的倾斜角α与其斜率的变化关系.

教师引导：因为α∈［0，π），而斜率k=tan αα≠π2，所以可以用正切函数y=tan x，x∈[JB（［]0，π2[JB）]∪π2，π的图象进行动态演示（如图3）.

设计意图：使学生理解直线的倾斜角和斜率分别是从“形”和“数”两个角度刻画直线相对于x轴的倾斜程度，同时体会数学中“数”与“形”的完美统一，能真正理解并掌握直线倾斜角和斜率的辩证统一，培养思维品质和理性精神，树立正确的价值观.

例2 （1）已知O（O为平面直角坐标系的坐标原点）是等腰直角三角形OAB的直角顶点，点A在第一象限，∠AOy=15°，则斜边AB所在直线的斜率为[CD#3].

（2）若直线l的倾斜角α的变化范围是[JB（［]π6，π3[JB）]，则直线l斜率的取值范围是[CD#3].

问题导向：我们知道两点确定一条直线，如果已知直线上两点的坐标，那么这条直线的倾斜角就唯一确定，若直线l的倾斜角不为90°时，其斜率唯一确定.那么，直线的斜率和此直线上两点的坐标有什么关系呢？

探究4：用直线上任意两点的坐标表示斜率.

学生小组合作学习5：

（1）已知直线上的两点A（a1，a2），B（b1，b2），运用上述公式计算直线AB的斜率时，与A，B两点的顺序有关吗？

（2）当直线平行于y轴或与y轴重合时，上述公式还适用吗？为什么？

设计意图：提醒学生在研究直线斜率问题时，要根据题意分析是否需要讨论斜率存在与不存在两种情况，培养学生分类讨论和数形结合的数学思想，以及数学运算核心素养.

例3 （1）已知三点A（3，1），B（－2，t），C（8，1）能构成三角形，则实数t的取值范围是[CD#3].

（2）已知点M（x，y）在函数y=－2x+8，x∈［2，5］的图象上，则y+1x+1的取值范围是[CD#3].

探究5：建立直线的方向向量与斜率的关系.

问题6 我们知道，直线的方向向量为直线P1P2上的向量P1P2以及与它平行的非零向量，那么直线的斜率与直线的方向向量有什么关系呢？

学生自主探究，教师总结：

（1）若直线l的斜率不存在，即直线与x轴垂直时，则它的一个方向向量的坐标为（0，t）（t≠0）；

（2）若直线l的斜率为k，则它的一个方向向量的坐标为（1，k）.

以上即建立了直线的方向向量与斜率的关系.

设计意图：让学生理解直线的斜率和直线的方向向量的内在联系，培养学生把握事物关联的理性思维品质.

例4 （1）若直线l的方向向量是（1，sin θ），则此直线倾斜角的取值范围是[CD#3].

（2）若直线l的方向向量是（3，sin θ），则此直线倾斜角的取值范围是[CD#3].

3 教学反思，提高认识

3.1 重视概念生成，提升数学抽象素养

本节课以直线的倾斜角和斜率为载体，重在发展学生的数学抽象核心素养，通过将平面中确定一条直线位置的几何要素（点和方向），抽象为在平面直角坐标系中确定一条直线位置的量，进而抽象出倾斜角的概念，然后由“形”到“数”，抽象出斜率的概念，进而得到直线方向向量的概念.通过概念教学，提升了学生数学抽象核心素养.

3.2 重视问题驱动，提升直观想象素养

在教学方法上，利用如何在平面直角坐标系中确定一条直线位置的问题设计，以及如何理解直线的倾斜角和斜率的概念等，采用问題驱动，让学生小组合作、主动探究，将课堂主动权真正交给学生.学生通过直观想象、合作探究和教师引导的概念教学，提升了直观想象核心素养［２］.

3.3 重视知识反馈，提升数学运算素养

在课堂教学中，学生不仅要能理解倾斜角和斜率及直线的方向向量等重要概念，还要能应用概念解决数学实际问题.通过设计典型例题解析，加深学生对概念的理解，能应用概念正确解决问题，提升学生数学运算核心素养.

参考文献：

[1]中华人民共和国教育部.普通高中数学课程标准（2017年版）［S］.北京：人民教育出版社，2018.

[2]马清太，尹祖荣.核心素养下的单元教学设计——以“三角函数概念”为例［J］.中学数学教学参考，2022（7）：17-20.