以史为鉴,重构课堂
2024-05-14王保红梁诗晗
王保红 梁诗晗
1 问题提出
《普通高中数学课程标准(2017年版2020年修订)》在课程结构中明晰了“数学文化融入课程内容”的要求,阐明了“数学的思想、精神、语言、方法、观点,以及它们的形成和发展”是数学文化的重要内容.
“指数函数与对数函数”是高中数学教学的核心内容之一.课标要求“收集、阅读对数概念的形成与发展的历史资料,撰写小论文,论述对数发明的过程以及对数对简化运算的作用”等不作为考试内容的要求.人教A版高中数学新教材必修第一册“对数的概念”两处融入了数学史.“阅读与思考”中,“对数的发明”在于培养学生创新思维,使学生通过数学阅读加深对数学知识的深层次理解.“文献阅读与数学写作”中,“对数概念的形成与发展”是新增设的版块,目的是希望学生自主了解数学知识形成与发展的脉络,感受数学文化.本文中以“对数的概念”教学为例,力求在教学中适当融入数学史,以期为高中数学教学提供参考.
2 梳理对数的发展历史
2.1 对数思想的萌芽
约公元前1700年巴比伦泥版上出现了类似解指数方程的题目.15世纪法国数学家许凯(N.Chuquet)在《算术三部》提出了解指数方程的问题,还列出了等比和等差数列,即1,2,4,8,16,……,1 048 576和0,1,2,3,4,……,20,指出数列对应关系:上一列数的乘除运算结果对应下一列数的加减运算结果.
16世纪涌现出了许多研究等比数列乘法法则的数学家.德国数学家斯蒂菲尔(M.Stifel)提出了四条乘法法则,即几何级数中的乘法、除法、乘方、开方与算术级数的加法、减法、乘法、除法对应,还将法则推广到负指数,形成双数列对应关系.
天文、航海等领域要求大数运算.而想要算出一个复杂的数据,需长达几年的时间.因此,迫切需要改进数字计算方法,以提高计算速度和准确度.
2.2 对数方法和思想的产生
苏格兰数学家纳皮尔(J.Napier)研究大数运算,最终发明了对数,并将对数(logarithm)意为“比的数”.1614年出版的《奇妙的对数定律说明书》标志着对数的诞生.英国数学家布里格斯(H.Briggs)与纳皮尔商定了“旷世之约”:1的对数为0,10的对数为1.布里格斯制作
的常用对数表更容易算出数值,将底数为10的对数称其为常用对数,底数概念也由此诞生.法国数学家拉普拉斯(P.S.Laplace)评价道:“因为省时省力,对数倍增了天文学家的寿命.”
瑞士仪器制造者比尔吉(J.Burgi)也独立发现了对数并用它来造表.1620年他出版了《等差数列和等比数列》,尽管那时纳皮尔发明的对数已闻名欧洲.18世纪瑞士数学家欧拉发现指数与对数的互逆关系,指出“对数源于指数”.
2.3 自然对数的由来
使用常用对数时发现N与其对数并非同时均匀增长,为了寻求能使两边对称的底数,让式子化繁为简,发现若以e作底数最“自然”,符合数学的对称美和简洁美.故以e为底的对数叫“自然对数”,亦定义logeN=ln N,在科技、经济中有广泛应用.
3 基于数学史的对数概念教学
3.1 教学思路
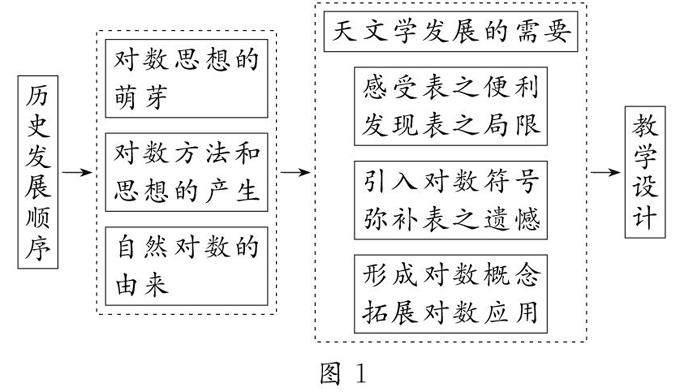
依据对数历史,整体采用重构式的设计(如图1),借鉴对数历史,追溯思想起源,呈现知识自然发生的过程.
3.2 重构对数概念的数学课堂
3.2.1 天文学发展的需要
例1 随着科技的发展,人类对宇宙的探索愈加深入.天文学定义,光在真空中的速度为299 792.468 km/s,一年的总秒数是31 536 000 s,能否动笔求出一光年的值?
(列式为299 792.468×31 536 000=?)
师:介绍对数产生的原因.该如何简化运算?
设计意图:利用生活实例创设情境,使学生感受大数运算的不易,由此产生探究简化大数运算的想法.
3.2.2 感受表之便利,发现表之局限
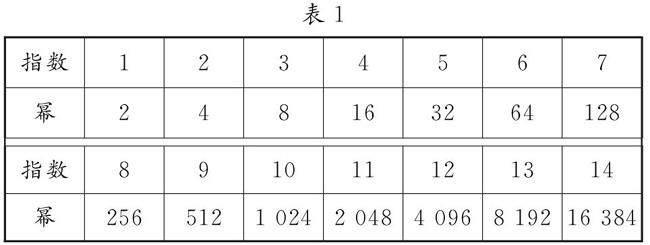
例2 展示斯蒂菲尔双数表(表1),让学生观察规律.
师:第二行中后一个数是前一个数的两倍.若第1行表示2的指数,则第2行表示其对应的幂.16世纪数学家斯蒂菲尔在研究上表时,把第一行的各项称为“指数”.他还发现第一行指数相加得到其乘积的指数,指数相减得到其商的指数.
师:求32×512,先找到32和512在数表中对应的第一行的数.即32对应5,512对应9;将二者相加,即5+9=14;再找到14对应的下一行数为16 384.
师:按照规律,能否快速求出下列各式子的值?
16×1 024;8 192÷32;643;81×729.
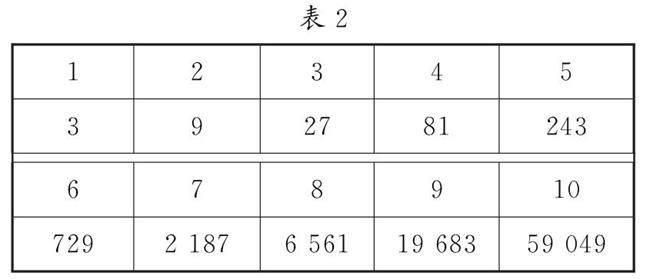
上面有些数并不能从数表中查到,该如何解决?发现81与729两个数都能变成以3为底的幂的形式,但查不到.法国数学家许凯也曾遇到这样的问题,而且是在斯蒂菲尔之前.相对于自然数列而言,他研究的双数表可表示2或3的指数.
例3 请大家根据许凯双数表(表2)完成计算.
师:如果算式是其他数呢?由于第二行相邻两项的差值越来越大,数便难以找到.当时的天文学家对此非常苦恼.于是数学家开始制作更加详细的数表.其中贡献最大的是纳皮尔(可介绍纳皮尔与对数).例1该怎么解决?
找到299 792.468和31 536 000分别对应的数,先求和再查表.令2x=299 792.468,2y=31 536 000.
追问:整数可以通过查表得到,小数点后几位怎么算?如何得到精确值?
设计意图:根据乘法法则,让学生经历简化运算的过程,感受查表的便利.讲述纳皮尔贡献,培养学生科学精神和探究意识.利用提示语启示学生发现对数表的局限性,引出新知识.
3.2.3 引入对数符号,弥补表之遗憾
师:之前是否遇到过类似的难题?初中是如何计算x2=2的?在学习“[YY(]1[YY)]”后,我们解决了非完全平方数的平方根问题.同理,当现有知识不足以解决问题时,需要创造新的符号来表示.数学家将对数“logarithm”简写为“log”.这样就解决了像例1中这种“天文数字”的计算.引用数学家对对数的评价.
设计意图:借助旧知,引入新知.体会引入符号的必要性,弥补数表局限的遗憾.
3.2.4 形成对数概念,拓展对数应用
师:观察对数,思考它与指数有何关系?
追问:二者可以互相转化,即对数logaN与指数互逆.对数中a的取值范围是什么?
回顾指数概念.得到对数概念:一般地,若ax=N(a>0,且a≠1),那么数x称为以a为底N的对数,记作x=logaN,其中a叫作底数,N叫作真数.当a>0且a≠1时,ax=Nx=logaN,这是互化公式.计算方便,又能比较大小.0和负数没有对数.
利用数学家轶事讲解常用对数.把常用对数log10N记作lg N.总结:logaa=1,loga1=0,log10N=lgN.由常用对数引出自然对数.
设计意图:暗示学生指数与对数存在互逆关系;渗透数学史,将知识自然呈现;强调一般对数与常用对数、自然对数之间的转化.
3.2.5 巩固练习,总结课堂
(1)在巴比伦泥版上有一道复利题目1.2x=2,请求解.
(2)将指数式化为对数式,对数式化为指数式(教材例题).
设计意图:帮助学生整理思路,感受对数在简化运算方面的作用,总结现实应用.
4 总结与反思
数学史对于数学教育有重要意義.数学史可以帮助学生清除认知障碍,同时数学史也是一面镜子,把当时思想的碰撞反映到数学知识的学习中.对教师而言,将数学史融入数学教学,可以帮助教师根据学生认知障碍设计教学,提升教书育人的能力,提升数学素养.对学生而言,可以帮助他们了解知识的由来与发展,理解数学知识,体会其中蕴含的思想,提升科学精神,培养数学核心素养.
