F+CHD3→HF+CD3 反应C—H 伸缩振动激发的量子动力学研究*

周勇

(安徽师范大学物理与电子信息学院,芜湖 241000)

对多原子化学反应进行精确的理论模拟研究,是当前量子动力学领域的重要挑战之一.本文运用七维的量子含时波包方法,对反应物振动基态和C—H 伸缩振动第一激发态的F+CHD3 反应进行动力学研究.分析了不同振动态条件下的反应概率,发现当碰撞能低于0.06 eV 时反应概率曲线均表现出许多剧烈的振荡峰,支持实验上所推测的动力学共振现象.当碰撞能介于0.06—0.3 eV 之间时,振动激发态反应中HF 产物通道的反应概率低于振动基态反应,与实验观测结果一致.模拟发现: 相比于振动基态的情况,低能碰撞时C—H 伸缩振动激发态反应的非含时波函数在过渡态区域更倾向于靠近D 原子一侧,并将这一现象归结为振动激发态势能面在大碰撞角区域更显著的能量优势,解释了伸缩振动激发对HF 产物通道的抑制作用.本研究为实验结果的解释提供了重要的理论支持,有助于更深入地理解多原子反应中振动模式激发对动力学过程的影响.

1 引言

过去几十年中,气相化学反应的精确理论研究取得了很大的进展.尤其是随着含时波包方法的发展,现在已经可以在没有动力学近似的情况下,对四原子反应进行初始态选择的研究[1,2].理论工作者报道的关于H+H2O → H2+OH 反应[3]和HD+OH → H2O+D 反应[4]微分截面的研究结果,标志着对四原子反应问题的理论解决已经接近尾声.目前,在量子动力学领域的一个主要挑战是发展用于研究包含多于4 个原子化学反应的精确方法.

作为重要的多原子反应体系,F+CH4反应及其同位素取代反应近年来吸引了来自实验和理论方面的广泛关注[5-11].Liu等[12]利用“离子速度成像”(velocity map ion imaging)技术获得了F+CH4反应的配对相关的(pair-correlated)态分辨激发函数;通过研究反应能量阈值附近出现的“台阶”现象,他们推测该反应中可能存在反应共振现象[13].Liu 及其合作者们[14]还使用类似的实验技术研究了F+CHD3反应HF 通道产物对之间的模式相关性(mode correlation),并依据在反应积分截面的低能区域所发现的明显台阶特征,推测该反应通道也存在反应共振[15].理论研究方面,Troya等[16]将CH3看作伪原子构造了三维的基态解析势能面,并基于此势能面的准经典轨线研究复现了实验上测得的HF 内态分布,证实了实验中发现的立体反应动力学现象.Espinosa-Garcia等[17]构造了F(2P)+CH4及其同位素反应的势能面,并将其用于反应速率常数计算和动力学研究.Czakó等[18]构建了F+CH4体系的全维全域势能面,在此基础上进行的准经典轨线计算得到了和实验结果吻合的HF 产物振转分布.Nyman 和Espinosa-Garcia[19]基于三维量子散射模型的计算,为F+CH4反应中的共振现象提供了理论证据.Wang 和Czakó[20]在四维量子动力学计算得到的总反应概率和积分截面中发现了反应共振的相关特征.Westermann等[21]基于全维的多组态含时Hartree(MCTDH)方法计算了F+CH4反应的过渡态光谱,发现了反应入口通道范德瓦耳斯(vdW)势阱里的反应共振.von Horsten和Clary[22]对F+CHD3反应进行的两维量子动力学研究,计算了两个产物通道末态分辨的反应概率和截面,并分析了低能碰撞区域处的共振态.Qi等[23]和Zhao等[24]分别开展了F+CHD3反应的八维和七维波包动力学计算,均报道了低碰撞能条件下总反应概率曲线上的快速振荡结构,并将之归结为反应前的vdW 势阱.最近,Zhang 课题组构建了一个新的F+CH4 反应势能面[25]并报道了对F+CHD3→HF+CD3振转基态反应的六维态-态量子动力学研究结果,在总的和态分辨的反应概率曲线中观察到显著的振荡结构并将其归结为由HF 化学键软化所导致的HF(v'=3)-CD3振动绝热势阱[26].

Zhang等[27]开展了对F+CHD3反应中的C—H键伸缩振动激发的实验研究.对于这一早期势垒(early barrier)反应,根据经验推测反应物的振动应该不会和反应坐标有效耦合,因此对反应产出的影响很小;然而,实验中发现C—H 键的伸缩振动激发反而抑制了C—H 键的断裂,即倾向于DF+CHD2产物通道.Czakó等[28]通过对F+CHD3(vC—H=0,1)反应准经典轨线的统计分析发现: C—H键的伸缩振动激发会导致F 原子在反应鞍点区域倾向于靠近C—D 键.虽然这一发现可以在一定程度上解释C—H 键伸缩振动激发对C—H 键断裂的抑制作用和实验上所观察到的键选择性现象,但是对于F 原子接近CHD3分子时会偏向于D 原子一侧的原因,Czakó等[28]并未给出更进一步的解释.此外,受准经典轨线方法本身的限制,其仅能对F+CHD3反应进行比较粗糙的描述,例如其很难精确捕捉F+CHD3振动激发态反应中可能存在的量子反应共振现象.

量子理论可以为化学反应动力学过程提供最精确的描述.然而,与H+CH4,H+CHD3,H+CD4等被广泛研究的六原子反应体系[29-33]相比,对F+CHD3反应的量子波包动力学研究更加具有挑战性.一方面,入射原子由质量较小的H 原子变为质量较大的F 原子,对于可能发生共振现象的低能碰撞,波包需要传播的时间要长得多;其次,由于F 原子和CHD3分子之间存在长程相互作用,为获得更准确的结果,需要将初始波包的位置放在很远的位置(大于15 Bohr),这将进一步延长波包的传播时间.本文采用七维的含时波包方法,研究了振动基态和C—H 伸缩振动第一激发态F+CHD3反应当总角动量Jtotal=0 的情况,发现低碰撞能情况下反应概率曲线上均出现了暗示反应共振的强烈振荡现象,重现了实验上观测到的C—H 键伸缩振动激发对HF 产物通道的抑制现象,并基于振动态平均的势能面对反应中的键选择性进行了解释.

2 理论方法

2.1 X+YCZ3 型反应的量子含时波包方法

图1 定义了用于研究X+YCZ3→XY+CZ3型反应的八维Jacobi 坐标系统.R为从YCZ3分子的质心到X 原子的向量,r为从CZ3基团的质心到Y 原子的向量.s为C—Z 键的键长,在7D 计算中该键长被固定为反应物C—Z 键的平衡键长.χ为C—Z 键和CZ3基团的C3V对称轴的夹角.为描述角度坐标和系统的转动,这里引入了4 个框架,分别为空间固定(space-fixed)框架、XYCZ3固定框架、YCZ3固定框架和CZ3固定框架.YCZ3框架的z轴沿着向量r,向量s总是在该框架的xz平面上.CZ3固定框架的z轴沿着其对称轴,同时第一个Z 原子始终在此框架的x-z平面中.定义R和r之间的弯曲角为θ1,r和s之间的弯曲角为θ2,YCZ3围绕向量r的扭转角为φ1,CZ3基团围绕其对称轴的扭转角为φ2.

图1 用于研究X+YCZ3 反应的8 维Jacobi 坐标系统Fig.1.8D Jacobi coordinate system for X+YCZ3 reactions.

基于八维模型的X+YCZ3反应的哈密顿量用上述Jacobi 坐标表示为[29,34]

含时波函数用宇称匹配(parity-adapted)的转动基组展开为

对应于某个态(Jtot,M,ε) 的系统初始波函数写成局域波包G0(R) 和对应于(n0,J0,K0,p0) 状态下YCZ3的本征函数这两部分的直积,其中n0,J0,K0,p0分别表示初始振动态、总角动量及其在XYCZ3固定框架z轴上的投影和YCZ3分子的宇称.

本工作使用“分裂算符”方法进行波函数的传播:

其中参考哈密顿量H0定义为

而参考势能U定义为

对应于某个特定初始态的在整个能量范围内的总反应概率,可以首先通过对含时波函数进行傅里叶变换得到非含时波函数ψiE,然后在分割面r=rs上对非含时波函数及其一阶导数积分得到:

2.2 计算参数

本文使用2.1 节中所介绍的方法对F+CHD3反应进行研究.为了减小计算中所用基组的大小,对R和r坐标进行“L 形”的波函数展开.R坐标的取值范围为3—21 Bohr,共使用302 个正弦基组,其中在相互作用区域共使用98 个格点.对于r方向,反应渐进区和相互作用区分别使用7 个和50 个基函数.C—D 键的长度固定为反应物CHD3分子的平衡键长(2.06 Bohr);同时,使用了9 个基函数来描述CD3基团的伞形振动.约束转动基函数大小的参数分别为Jmax=114,lmax=90,jmax=24和kmax=24.在考虑了CD3基团的C3V对称性的情况下,展开波函数时共使用了284927 个转动基函数,在对转动基函数进行数值积分的过程中共使用了2394875 个角度格点.高斯波包的初始中心位于R0=18.5 Bohr,波包宽度δ=0.2 Bohr,波包中心能量为E0=0.2 eV.本工作中采用的是Czakó等[18]构造的全维全域势能面.

3 结果与讨论

图2 显示了总角动量Jtotal=0 情况下,反应物振动基态和C—H 键伸缩振动第一激发态的总反应概率随碰撞能的变化.由图2 可知,无论反应物是处于振动基态还是振动激发态,反应的能量阈值均非常小.Czakó等[18]在UCCSD(T)/aVTZ 水平上进行的电子结构计算表明,该反应的反应能垒很低,仅为0.5 kcal/mol 左右.考虑到该H 原子抽取反应通道可能存在的隧穿(tunneling)效应,这里看到的低反应能量阈值情况与Czakó等[18]的计算结果吻合.在当前所考虑的碰撞能范围内,总反应概率的最大值可以达到15%左右,远远高于H+CH4及其同位素反应的相关结果(约0.3%),这表明了F 原子具有更强的反应活性.

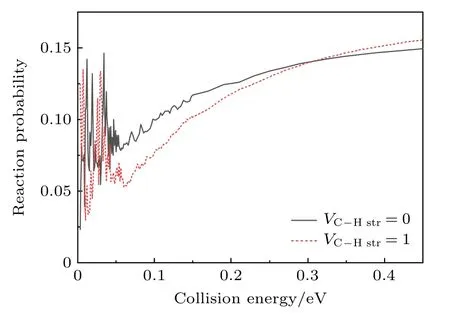
图2 总角动量Jtotal=0 时,F+CHD3 (vC—Hstr=0,1) →HF+CD3 反应的总反应概率Fig.2.Total reaction probabilities of the F+CHD3 (vC-Hstr=0,1) → HF+CD3 reaction with total angular momentum Jtotal=0.

对于反应物处于振动基态的情况,当碰撞能Ec＜ 0.06 eV 时,反应概率随碰撞能剧烈变化并形成了许多尖锐的振荡峰.这一现象与Liu等[26]基于神经网络势能面所进行的六维量子波包结果吻合得很好,说明反应过程中确实存在共振现象.从Ec=0.06 eV 附近开始,随着碰撞能量的增大,反应概率随碰撞能的振荡现象减弱,同时反应概率缓慢增大.Zhou等[15]在实验中发现,当碰撞能小于1.2 kcal/mol(0.052 eV)时,反应激发函数曲线中会出现明显的“台阶”特征,并据此推测反应中可能存在共振现象.这一点现在也被本工作的理论模拟结果所支持.此外,实验结果还显示,当碰撞能升高至0.052 eV 附近时激发函数会明显增大,本工作模拟得到的总反应概率中也发现了类似的现象.此外,von Horsten 和Clary[22]的二维量子动力学研究也发现: 在低能(Ec＜ 6 kJ/mol,合0.062 eV)碰撞区域,共振结构起主导作用;在5—6 kJ/mol的碰撞能附近,由于HF (v'=3)产物通道的打开,总反应概率也会突然增大并且随着碰撞能的增大而上升.这些结果也都与本工作的模拟结果一致.

对于反应物C—H 键伸缩振动第一激发态的情况,反应概率随碰撞能的变化曲线与基态反应情况类似: 当碰撞能Ec＜ 0.06 eV 时,可以看到许多明显的振荡峰;随着碰撞能的增大,反应概率逐渐增大.不同的是,当碰撞能Ec在0.06—0.3 eV 范围内时,振动激发态的反应概率要小于基态反应;这一现象与Zhang等[27]的实验结果在定性上吻合得很好.定量而言,理论得到的基态反应概率最大仅为激发态反应概率的1.5 倍左右,这与实验结果[27]测得的反应激发函数比值(5—10 倍)差别仍比较大.为了实现理论与实验之间的一对一比较,后续有必要进一步地计算振动激发态的反应积分截面.

Zhou等[15]进行的实验研究表明,对于振动基态反应,当碰撞能小于1.2 kcal/mol(合0.052 eV)时,生成的HF 产物基本上完全处于v′=2 振动态.为从理论上证明这一点,图3 给出了低能碰撞情况下产物通道的非含时波函数.这里采用了与三原子态-态反应研究中“反应物→产物”坐标变换类似的方法,以便更清楚地观察产物的振动态特征.图3中竖直方向为产物反应坐标,其中下方为反应过渡态区域,上方为产物渐进区;水平方向对应于HF产物坐标.图3(a)显示了振动基态反应、碰撞能Ec=0.018 eV 的情况.由图3(a)可知,在产物渐进区域波函数仅能分辨出2 个节点,此时波函数对应于HF 产物伸缩振动的v′=2 态,这一点与实验观察到的结果[15]吻合.在反应过渡态区域波函数沿着水平方向出现了3 个明显的节点,说明在该区域HF 伸缩振动对应于v′=3 激发态;Liu等[26]基于神经网络势能面所进行的六维量子波包模拟也发现了类似的现象,并将过渡态区HF(v′=3)态到产物渐进区HF(v′=2)态的转变归结为Feshbach共振.

图3 产物通道的非含时波函数(a)振动基态,碰撞能Ec=0.018 eV;(b) C—H 键伸缩振动第一激发态,碰撞能Ec=0.025 eV;图中竖直方向和水平方向分别对应散射坐标和HF 产物坐标Fig.3.Time-independent wave function in product channel:(a) Ground vibrational state with collision energy Ec=0.018 eV;(b) the first C—H stretching vibrational excited state with collision energy Ec=0.025 eV.The vertical and horizontal directions correspond to the scattering coordinate and the HF product coordinate,respectively.

量子化学计算结果[15]表明,对于振动基态反应,当反应碰撞能Ec＞1.14 kcal/mol(0.05 eV),HF(v′=3)产物通道将打开.我们计算得到这一振动激发态的激发能为0.369 eV,这一数值与Czakó和Bowman[35]使用变分组态相关(variational configuration interaction)方法计算得到的结果2985 cm-1(0.370 eV) 吻合得非常好.因此,从可资用能量的角度推测,对于C—H 键伸缩振动第一激发态,即使对于很低的碰撞能,也可能会生成HF(v′=3)产物.图3(b)显示了CHD3分子C—H键伸缩振动第一激发态、碰撞能Ec=0.025 eV 时的产物通道非含时波函数.由图3(b)可知,在反应过渡态区域附近,与图3(a)中振动基态的情况类似,波函数沿着水平方向也表现为3 个节点,对应HF(v′=3)态.然而,与振动基态情况不同的是,随着产物反应坐标从过渡态区域变化到产物渐进区域,振动激发态反应的产物波函数仍然保留着3 个节点的特征,对应于HF(v′=3)产物.此点与上述基于能量分析的推测结果一致.

为了研究伸缩振动激发抑制C—H 键断裂的原因,选择两个有代表性的碰撞能,分别为0.06 eV和0.2 eV.由图2 可知,当碰撞能Ec=0.06 eV时,反应物伸缩振动第一激发态所对应的反应概率明显低于振动基态情况(相对差别～35%);而当Ec=0.2 eV 时,二者反应概率则非常接近(相对差别约4%).

采用与之前研究H+CD4反应[29]时类似的做法,图4 显示了碰撞能Ec=0.06 eV 时,反应物区域的非含时波函数随反应坐标R、入射F 原子倾斜角θ(即图1 中定义的θ1)变化的情况.对于反应物处于振动基态的情况(图4(a)),反应坐标R=9 Bohr 处的波函数在大倾斜角和小倾斜角区域的分布之间差别不大.随着趋近于过渡态区域,可发现波函数在大倾斜角区域的分布逐渐增多,即H 原子逐渐偏离C—H 键并向C—D 键靠拢.类似地,Czakó和Bowman[36]对准经典轨线的统计分析也表明,振动基态情况下入射F 原子较靠近C—D键和较靠近C—H 键这两种情况的比例大约为3∶1,与CHD3分子中对应原子数目的比值相近.图4(b)显示了反应物处于C—H 键伸缩振动第一激发态的情况.与振动基态情况类似,随着波函数向过渡态区域逐渐靠近,其更加倾向于分布在大倾斜角一端.不过,与振动基态情况不同的是,当C—H 伸缩振动模式被激发后,过渡态区域附近的波函数在小倾斜角区域的分布要明显变少;绝大部分波函数分布在大倾斜角区域,并在倾斜角θ=140°—160°附近积聚成很高的峰.这一区别将直接导致C—H 键伸缩振动激发所对应的HF 产物生成概率大大减小.之前Czakó和Bowman[36]所进行的准经典轨线分析表明: C—H 伸缩振动激发情况下入射F 原子较靠近C—D 键和较靠近C—H键这两种情况的比例远远高于D/H 原子数目之比(最高可达11 左右).这一点与图4(b)中所展示的结果在定性上也是一致的.

图4 碰撞能Ec=0.06 eV 时,反应物区的非含时波函数随反应坐标R 和入射F 原子倾斜角θ 的变化(a)振动基态;(b) C—H键伸缩振动第一激发态Fig.4.Time-independent wave functions in the reactant region as a function of reaction coordinate R and the inclination angle θ of incoming F atom at a collision energy of Ec=0.06 eV: (a) Ground vibrational state;(b) the first C—H stretching vibrational state.

图5 展示了碰撞能Ec=0.2 eV 时,对应于反应物振动基态和C—H 键伸缩振动第一激发态的非含时波函数.对于振动基态的情况(图5(a)),与低碰撞能结果(图4(a))类似,反应过渡态处的波函数同样具有较大的比例分布在小碰撞角区域.类似地,对于振动激发的情况(图5(b)),即便是当非常靠近过渡态时,在小倾斜角区域也仍然分布有较多的波函数,这一点与图4(b)中所示的低碰撞能情况有明显不同.通过比较图4(b)和图5(b)可知,的确可以将C—H 键伸缩振动激发对HF 产物通道的抑制作用归结为入射F 原子相对于C—H键的偏离.

图5 碰撞能Ec=0.2 eV 时,反应物区的非含时波函数随反应坐标R 和入射F 原子倾斜角θ 的变化(a)振动基态;(b) C—H键伸缩振动第一激发态Fig.5.Time-independent wave functions in the reactant region as a function of reaction coordinate R and the inclination angle θ of incoming F atom at a collision energy of Ec=0.2 eV: (a) Ground vibrational state;(b) the first C—H stretching vibrational state.

为了解释C—H 键伸缩振动模式被激发时入射F 原子偏离C—H 键的原因,接下来进一步分析不同振动模式下反应的有效势能(effective potential).这里借鉴了前人研究H+H2O 反应时所采用的分析方法[37],将势能对C—H 键的键长r进行平均,即:

其中,ϕv1(r) 是C—H 键的振动本征函数,Vref(r)是r方向的参考势.如图6 所示,当反应坐标R值较大,即远离反应过渡态区域时,反应物振动基态和C—H 键伸缩振动第一激发态的平均势能之间差别不大.随着逐渐靠近强相互作用区域,两个不同振动态对应的势能面均开始向大倾斜角倾斜.对于振动基态势能面,小倾斜角和大倾斜角区域之间的差别相对不那么显著;而当C—H 键伸缩振动模式被激发之后,与基态势能面相比,小倾斜角区域的势能有小幅度的升高,同时大倾斜角区域的势能则进一步的降低.从能量优势的角度而言,振动激发情况下,波包将更倾向于以类似于“坐滑梯”的方式达到大倾斜角区域,从而导致了入射F 原子偏离C—H 键而向C—D 键靠近.这一点同时也印证了Zhang等[27]之前为解释实验结果所推测的、F 原子与伸缩振动激发的C—H 键之间相互作用的各向异性改变.

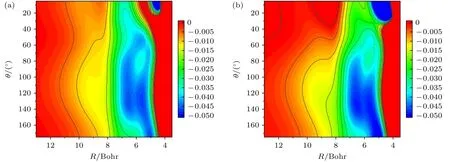
图6 振动态平均的反应有效势能随反应坐标R 和入射F 原子倾斜角θ 的变化(a) 振动基态;(b) C—H 键伸缩振动第一激发态Fig.6.Averaged effective potential energy over vibrational states as a function of the reaction coordinate R and the inclination angle θ of incoming F atom: (a) Ground vibrational state;(b) the first C—H stretching vibrational excited state.

4 结论

本文采用七维量子含时波包方法研究了反应物振动基态和C—H 伸缩振动第一激发态的F+CHD3反应动力学.在总角动量为0 情况下,当碰撞能低于0.06 eV 时振动基态的反应概率曲线上出现许多尖锐的振荡峰,与前人基于不同减维模型或势能面所得到的理论模拟结果吻合得很好,支持实验上所推测的动力学共振现象.当碰撞能低于0.06 eV 时,振动激发态的反应概率曲线也表现出类似于振动基态反应的剧烈振荡峰,暗示此时反应过程中也可能存在动力学共振现象.计算发现,对介于0.06—0.3 eV 之间的碰撞能,振动激发态反应HF 产物通道的反应概率低于振动基态反应,与实验观测结果一致.与前人的准经典轨线模拟结果类似,低碰撞能情况下振动激发态反应的非含时波函数在过渡态区域更倾向于分布在大碰撞角附近(D 原子侧);而对于高碰撞能情况,不同振动态下过渡态区域非含时波函数的碰撞角分布之间则差别不大.对反应有效势能的分析表明,相对于振动基态的情况,C—H 伸缩振动激发态势能面在大碰撞角区域的能量优势更加明显,由此导致伸缩振动激发对HF 产物通道的抑制作用.