基于Adam 算法的光学相控阵输出光束校准方法*

王子豪 龙烨 仇轲 徐佳木 孙艳玲 范修宏 马琳† 廖家莉 康永强

1) (西安电子科技大学光电工程学院,西安 710071)

2) (西安微电子技术研究所,西安 710000)

基于微纳集成的光波导相控阵芯片是近年来激光雷达技术领域的研究热点.随着激光雷达系统空间分辨这一实际应用需求的不断提高,作为激光雷达系统中的光束控制器件,光波导相控阵需要扩大阵列规模以提升输出光束的空间分辨率.同时也为光波导相控阵输出光束的优化校准带来了困难,现有算法不仅光束校准质量不高,且校准效率较低.为此,本文将Adam 算法应用于光波导相控阵输出光束校准系统中,通过建模仿真比较了Adam 算法与现有SPGD 算法和GS 算法在光束校准层面上的优劣.同时,搭建实验系统实现了高质量的光束校准,根据校准结果,在Adam 算法校准下光波导相控阵输出光束的主旁瓣比优于15.98 dB,对16×16 光波导相控阵输出光束校准达到收敛所需的迭代次数低于600 次.这一算法在光波导相控阵输出光束校准方面的应用,能够提高光波导相控阵的控制精度和效率,拓展光波导相控阵在激光雷达技术、数字全息技术和生物成像技术等方面的应用.

1 引言

随着无人驾驶技术的出现与应用,激光雷达技术受到各国研究者们的关注和重视.光波导相控阵(optical phased array,OPA)作为激光雷达技术的分支之一,具有集成化、低功耗和高精度的特点,是推动激光雷达技术乃至无人驾驶技术更进一步的重要助力.因此对于OPA 的研究、探索一直吸引着各国研究者们的目光[1-7].

2013 年,在DARPA 硅光子异构集成项目的支持下,MIT 对大规模二维硅基OPA 进行了关键器件和技术的研究,这是在Si 基OPA 领域上所取得的较高水平研究成果,这些成果极大地推动了OPA 领域的技术发展[8-11].2016 年,Mahon等[12]报道了单波长模式下的二维OPA,通过热光调制12 个均匀排布的天线阵列,实现了20°×2°的扫描范围.2019 年,Kim等[13]报道了一种新型热光调制OPA,他们采用正向偏置p-i-n 波导结构形成热光相位调制结构.实验实现了45.4°×10°的扫描视场及0.016 (°)/mW 热调制效率.

OPA 的发展过程从小阵列向大阵列集成的方向发展,这受益于CMOS 工艺的迅猛发展,不仅加工工艺大大提高,加工精度也不断取得快速进展.但对于OPA 技术而言,其是通过热光、电光、声光等方式改变晶体折射率[14,15],从而影响波导中传输光场相位来实现光束偏转的.相位是一个非常敏感的因子,任何由加工或键合带来的结构性差异都会导致OPA 芯片出现偏差,芯片阵列会存在未知的初相位,因而无法按照理论设计,加载控制电压实现光束的高质量定向偏转.

这亦引出了OPA 的新研究方向,即输出光束的校准控制技术.目前,有两类具有代表性的OPA 输出光束校准控制方法.第1 类为主动校准,Zheng等[16]提出了一种天线阵元干涉法,通过光学系统的加持,配合OPA 输出光束的近、远场切换,实现了极高质量的初相位测量,并进一步实现了高质量输出光束的校准.第2 类为被动校准,这种方法通过迭代算法,设置对应的评价函数,在预设的迭代规则下,配合相应的实验系统自动完成OPA 输出光束的校准.常见的算法包括爬山法、GS (Gerchberg-Saxton)法、退火法和SPGD (stochastic parallel gradient descent)法等[17-21].SPGD算法是一种应用广泛的梯度下降算法,多使用于控制变量较多,无法建立精确模型的系统中,具有精度高、可自定义性强等优点[22].GS 法作为一种相位检索方法,从已知的强度信息中恢复相位信息,多应用于光束整型和图像信息处理等领域[23].HIO(hybrid input-output algorithm)算法是一种在全息图像重建领域应用广泛的相位重构算法,其通过预设的推断来实现相位恢复,而非凭借数学推导和分析[24].但无论是主动或者被动校准,这些算法都面临同一个困境——随着OPA 阵列规模的扩大,校准的难度增加,精度大幅下降,效率大大降低,甚至个别算法还会出现迭代陷入局部最优解,导致光束校准效率低和结果质量差的问题.

Adam 算法是优化神经网络时非常重要的一种算法,它具有自适应学习率、快速收敛、对稀疏数据表现良好、适用于大规模数据、可计算梯度的低阶矩和无需手动调节超参数等优势[25,26].这些优势正好能解决OPA 阵列规模增大带来的输出光束校准困难和复杂的问题.在快速散射成像及运动目标散射成像等需要进行快速波前校准的应用场景中,收敛速度和校准质量是需要参考的指标.本工作将Adam 算法结合到OPA 输出光束校准系统中,通过特异性改动使其实现快速、高质量的光束优化,以提高光束校准水平.

本文将首先介绍Adam 算法的工作原理,及其在OPA 输出光束校准系统中应用的规则,进而建立仿真模型.对不同阵列的OPA 进行光束校准,比较各算法的光束校准质量与迭代次数的关系,分析论证Adam 算法在OPA 输出光束校准中应用的优越性.搭建OPA 输出光束校准系统,实验验证Adam 算法对OPA 输出光束的校准效果.

2 理论与仿真验证

2.1 OPA 输出光束校准

基于夫琅禾费多缝衍射理论对OPA 输出光的远场特性和偏转进行分析.二维OPA 输出波前偏转与各波导相位间的关系如图1 所示.图中a1和a2表示在x轴和y轴方向上单个天线宽度,d1和d2表示x轴和y轴方向上相邻天线间距,θ1和θ2表示在x轴和y轴方向上的偏转角,φ1和φ2表示x轴和y轴方向上相邻天线辐射场的相位差.由图1可知,当光波导相控阵的x轴和y轴方向相邻通道中光束相位差固定为φ1和φ2时,输出光的波前产生了定向偏转.

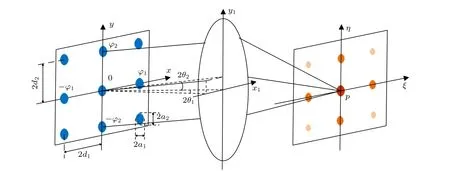
图1 OPA 夫琅禾费衍射示意图Fig.1.Schematic diagram of Fraunhofer diffraction in OPA.

基于夫琅禾费多缝衍射理论推导,当每个x轴和y轴方向相邻间天线输出光场的相位差相同为φ1和φ2且无外加电场时,在远场p点处的光场复振幅可以被表示为[27]

式中,M和N表示x轴和y轴方向上天线数量,Amn和φmn分别是第m行第n列的阵元出射光的振幅和相位.当出射平面与远场观测平面足够远时,各阵元到远场p点的距离近似为r=假设各φmn均为0时,则(1)式变为

远场p点对应的光强近似为

而在实际实验中由于器件加工误差和环境噪音等条件影响,各相邻阵元之间的初始相位差并不是相等的,导致OPA 存在未知相位差,其输出光束无法按照理论设计电压进行控制.因此需要利用控制算法进行光束校准[16-21],其本质上是一个最优化问题,可以写为

其中I(p) 为远场p点对应的实际光场,Iideal(p) 为远场p点对应校准光束理论最优光场.

2.2 算法与仿真

Adam 算法是一种自适应学习率的梯度下降算法,具有快速、简单、适用于大规模数据和稀疏数据的优点,广受关注[25,26].在OPA 输出光束校准的应用场景中,采用这些算法的目标是优化调制和相位控制,实现对输出光束的高度可控,从而提高精度和效率.在这部分工作中,优化的进程用评价函数J(p)表示,这里的评价函数可以是待优化区域的强度或目标光场与实际光场评判函数(可采用PSNR,SSIM 或MSE 等),在之后的仿真和实验中采用目标区域总光强与实际光场总光强之比作为评价函数.优化的目标是找到最佳相位控制,以最优化J(p).

经过优化和调参,本文所建立仿真模型中Adam算法中设定的3 个超参数值为: 学习率α=0.03、均值参数β1=0.9 和方差参数β2=0.999.以-0.005和0.005 二值伯努利分布生成施加在相位上的随机扰动,均值为0,方差相等.另外,还需要初始化初始电压u0.本文实验系统搭载Adam 算法中设定的超参数值为: 学习率α=20000、均值参数β1=0.9 和方差参数β2=0.999.但这些参数只针对本文所采用的实验系统,若采用不同系统请根据实际情况调整参数.本文拟采用迭代循环的方式运行Adam 算法,核心步骤包括更新梯度gt,计算均值向量mt,计算方差向量vt,计算修正后的均值向量mhat,计算修正后的方差向量vhat和迭代下一组电压ut.其中,需要注意修正均值向量和方差向量,以克服算法的运动或逆向运动困难问题.具体算法流程如图2 所示.

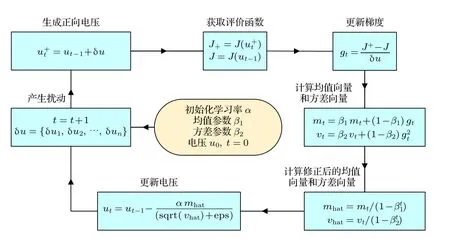
图2 OPA 输出光束校准的Adam 算法流程图Fig.2.Flowchart of the Adam algorithm for calibrating the OPA output beam.

本文所使用作为对照的SPGD 算法具体流程图如图3 所示.根据上述算法流程,本文分别对4×4,8×8,16×16 阵列的光波导相控阵的输出光束进行校准,具体仿真结果如图4 所示.根据图4结果可知,Adam 算法对任意阵列规模的OPA 校准效率都极高,且校准结果与理论值保持极高的一致性.

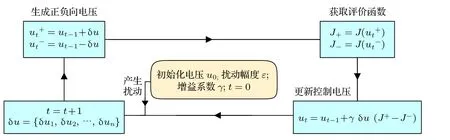
图3 OPA 输出光束校准的SPGD 算法流程图Fig.3.Flowchart of the SPGD algorithm for calibrating the OPA output beam.

图4 使用Adam 算法对不同阵列规模OPA 输出光束校准结果(a) 4×4 阵列校准结果;(b) 8×8 阵列校准结果;(c) 16×16 阵列校准结果Fig.4.Different adjusting results of output beam in serial OPA with Adam algorithm: (a) Adjusting results of 4×4 array;(b) adjusting results of 8×8 array;(c) adjusting results of 16×16 array.

各算法对不同规模的OPA 进行光束校准所呈现的评价函数曲线变化趋势及评价函数收敛值等表征是一致的.考虑到时间成本,本文在图5 中以4×4 规模的OPA 阵列为例,展示了不同算法光束校准时的质量和效率,以证明Adam 算法的优越性.对于OPA 输出光束校准系统而言,影响校准质量的因素主要有初始电压和初始步长.在图5 的仿真过程中,本文采用了相同的初始值,对阵元少的4×4 OPA 进行小步长输出光束校准时容易达到理论极限值,从而比较各算法在迭代完成后所达到的收敛值以及评价函数曲线变化趋势.

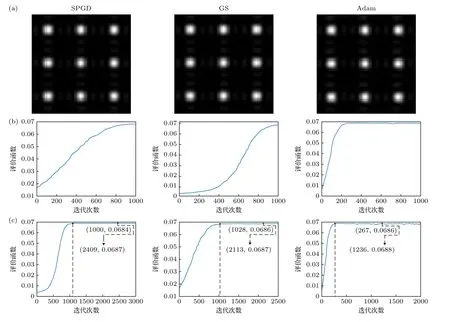
图5 使用SPGD,GS,Adam 算法对4×4 规模OPA 输出光束校准结果(a)不同算法优化仿真结果;(b) 优化迭代1000 次不同算法评价函数曲线图汇总;(c) 优化不限次数不同算法评价函数曲线图汇总Fig.5.Different adjusting results of output beam with SPGD,GS,Adam algorithm in 4×4 OPA: (a) Simulation results with different algorithms;(b) collection of curve graphs of evaluation function when iterating 1000 times with different algorithms;(c) collection of curve graphs of evaluation function when iterating unlimited times with different algorithms.

由图5(b)可知,相同迭代次数(1000 次)条件下,各算法只有Adam 算法稳定收敛到了理论极限值.如图5(c)所示,在不设置截止条件的情况下各算法都收敛于理论极限对应的评价函数值,Adam算法相较于GS 算法和SPGD 算法达到相同评价函数值所用迭代次数最少,其实现理论极限校准效果的效率最佳.此外,可以观察到即使在评价函数达到收敛后,Adam 算法由于其动态迭代步长调整机制,仍可能出现评价函数值的波动.为应对此现象,可以在实验过程实时记录每次迭代的评价函数值及其对应控制电压.这样即使在评价函数波动的情况下,也能够准确回溯到最佳控制电压.

3 实验系统及测试结果

实验系统示意图如图6 所示,本实验系统采用Koheras AdjustiK HP 型激光器输出波长为1550 nm 的激光,经过光纤输入OPA.实验所使用的二维16×16 OPA 与图4 仿真过程中使用的16×16 OPA 结构参数相同,该OPA 芯片的详细测试请参见文献[28].通过DSP 板控制OPA 的供电电路,给每个阵元按照算法加电以产生不同的输出光场.光场经过放大率为10 倍的物镜和焦距为250 mm 的透镜,由分辨率为640×512、像元尺寸为15 μm×15 μm 的红外相机Goldeye G-033TEC1接收并传回至DSP 板,通过如图2 所示的算法对接收到的光场进行处理,计算出新的电压加载到供电电路以实现光场迭代.这里以选取的待优化目标区域的总光强与采集图像的总光强的比值作为评价函数.在实验系统中加入了光学部分,通过调整光学元件间的距离或者替换相应器件将光场压缩到相机探测阵列的范围内进行优化,拓宽实验系统的扫描角度,实现对16×16 OPA 输出光束的最佳校准效果.

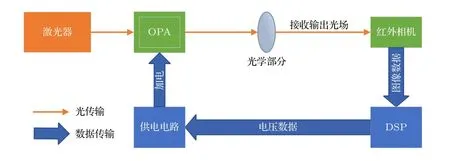
图6 实验系统流程图Fig.6.Flow diagram of experiment system.

实验采用峰值旁瓣比(peak side lobe ratio,PSLR)作为评价光束质量的参数之一,其定义为主瓣峰值强度IM与旁瓣最强峰值IS之间的比,单位为dB:

其理论最优值为26.94 dB.

图7 展示了以相同初始电压和初始步长进行光束优化的Adam 算法和SPGD 算法的实验结果.图7 中的算法优化结果是在相同相机曝光时间条件下获取的.由于相机输出的灰度图中最大强度值为255,因此选取此值作为归一化处理的标准,对两种算法的优化结果进行统一处理.这一作法旨在确保结果比较的公正性和科学性,以提高分析结果的准确性和可靠性.从图7 可以观察到,使用Adam算法校准的光场光强峰值旁瓣比优于15.98 dB,而使用SPGD 算法校准的光场光强峰值旁瓣比优于8.03 dB.进一步细化分析Adam 算法校准的光场,发现光束宽度和光斑位置与理论场分布具有较高的一致性.

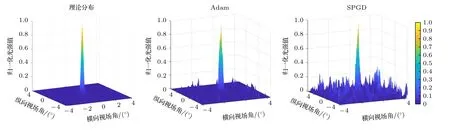
图7 仿真理论分布、Adam 算法及SPGD 算法输出光场三维图Fig.7.3D diagram of output light field with simulation model,Adam algorithm and SPGD algorithm.

如图8(c)所示,Adam 算法的评价函数曲线随迭代次数的变化呈现出明显收敛的趋势.在进行600 次迭代后,曲线趋于稳定,最高收敛值达到0.015,这表明Adam 算法在光束校准质量上表现出色.本文采用驱动电路的电压精度为1 mV,在该精度条件下OPA 输出光束校准已经实现收敛,还可以通过提高驱动电压精度实现更高质量的光束校准.此外,优化系统中红外相机采样所引入的额外噪声也可能会影响光束校准过程,因此通过使用信噪比更低的采集系统、采用基于统计模型的率噪方法、预先检验并校准红外相机各阵元、以及通过预检测调整红外相机参数等方法,以消除底噪并最大化信号与噪声的比例,从而有望实现更高质量的光束校准.因为本文主要介绍Adam 算法在OPA 输出光束校准上的应用,因此对这些方法不多做赘述.

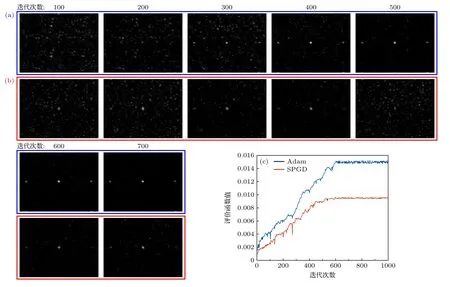
图8 SPGD 算法及Adam 算法光束校准效果图(a)不同迭代次数下Adam 算法光场灰度图;(b) 不同迭代次数下SPGD 算法光场灰度图;(c) Adam 及SPGD 算法评价函数曲线图Fig.8.Adjusting results of beam with SPGD and Adam algorithm: (a) Grey-scale map of different iterative times with Adam algorithm;(b) grey-scale map of different iterative times with SPGD algorithm;(c) curve graph of evaluation function with Adam and SPGD algorithm.

相比之下,SPGD 算法的评价函数曲线也在第600 次迭代后趋于稳定,但其收敛值为0.0095.由于两种算法起始于相同条件,理论上应达到相近的收敛值,然而SPGD 算法却在相同迭代次数内收敛于更低的值,这可能意味着该算法在优化过程中陷入了局部最优解.这一差异可以通过分析Adam算法的特性来理解.Adam 算法通过动态调整每个参数的学习率,实现了参数更新的精细化和高效化.这种自适应的学习率调整特性使得Adam 算法能够有效地应对评价函数值的波动,特别是在复杂的优化场景中,这有助于算法避免陷入局部最优解,并更接近全局最优解.因此,在相同的迭代次数内,Adam 算法不仅在光束校准质量上表现更优,而且在优化效率上亦更为高效.

为展示实验系统对视场中任意位置光束的优化效果,通过对不同位置的光束校准结果进行组合形成字母“XD”,如图9(a)所示.图9(b)也给出了部分位置的光束校准结果.由实验结果可以看出所采用的Adam 算法能够对视场中任意位置的成像光束实现高质量校准.

图9 (a)优化光场叠加图;(b)不同位置优化光场Fig.9.(a) Superposed figure of optimized light field;(b) optimized light field in different positions.

4 总结与展望

本文研究了用于OPA 输出光束校准的Adam算法,介绍了该算法用于OPA 输出光束校准的工作流程,通过仿真的方式比照分析了该算法与传统算法在OPA 输出光束校准上的优势,仿真结果表明该算法可实现OPA 输出光束的高质量和高效率校准.同时,采用该算法对16×16 二维硅基OPA输出光束进行校准,实现了15.98 dB 的主旁瓣比.实验结果表明,该算法能够对OPA 输出的光场进行校准,有效降低扫描栅斑,增强扫描主瓣的能量,增大探测距离,减小回波探测系统硬件方面的压力.

在进一步的研究中,探索并行运算的应用将是一个重要方向.初步分析显示,通过并行处理机制,算法有潜力高效处理大数据量,这对于复杂系统数据的处理具有重要意义.尽管现有算法在某些方面已表现出有效性,但为了满足高性能应用场景的需求,硬件优化和提升是必不可少的.

特别是,计算系统的算力提升、电控系统响应速度的增大以及数据传输效率的提高将是关键.这些改进不仅有望增强现有系统的处理能力,也为将技术推广至更高级别的光束校准系统奠定基础,为OPA 输出光束校准技术领域带来新的应用技术和前景.

感谢联合微电子中心金里博士为本工作芯片加工方面提供的帮助和支持.