反旋双色椭圆偏振激光场中Ar原子的非序列双电离

葛振杰 苏旭 白丽华

(上海大学理学院物理系,上海 200444)

利用经典系综方法研究了不同椭偏率的反旋双色椭圆偏振(two-color elliptically polarized,TCEP)激光场中Ar 原子非序列双电离(nonsequential double ionization,NSDI)的电子关联特性和再碰撞动力学.不同于反旋双色圆偏振激光场,反旋TCEP 激光场不再具有空间对称性,返回电子主要从一个方向返回母离子,从而导致电子动量分布表现出很强的不对称性.数值结果显示随着椭偏率的增大,Ar 原子NSDI 的产量逐渐减小,并且电子对在椭圆偏振激光场长轴方向上的关联电子动量分布,从主要位于第一和第三象限的正相关逐渐演变为主要位于第二和第四象限的反相关.通过对不同特征时间的统计分析表明,随着椭偏率的增大,旅行时间和返回电子的重碰撞能量逐渐减小,而延迟时间却增大,这是电子对关联特性发生变化的主要原因.此外,进一步分析发现,无论是“短轨迹”还是“长轨迹”,椭偏率的增大都会使两个电子由同向出射逐渐转变为反向出射,这表明椭偏率和旅行时间都影响着电子的出射方向.

1 引言

近年来,随着激光技术的发展,强激光场中原子分子的动力学问题越来越受到关注[1,2].当原子、分子与强激光场相互作用时,可以发现许多新的物理现象,如阈上电离[3-5]、强场光电子全息[6,7]、高次谐波的产生[8,9]和非序列双电离(nonsequential double ionization,NSDI)[10-12]等.近几十年来,由于NSDI 中存在强烈的电子关联现象[13-15],如碰撞激发电离(recollision-induced direct ionization,RII)[16,17]、碰撞激发场致电离(recollision-induced excitation with subsequent field ionization,RESI)[18]和NSDI 的多重碰撞[19]等,而引起研究人员的关注.

在强激光场与原子、分子相互作用时,NSDI过程可以用三步模型来解释[20,21].首先,当原子、分子处于强激光场中时,第1 个电子(返回电子)通过隧穿电离释放出来[22],然后释放的电子在激光场的驱动下回到母离子附近,并与第2 个电子(束缚电子)发生重碰撞[20,23].在这个过程中,由于两个电子发生了重碰撞,返回电子会将部分能量传递给束缚电子,束缚电子可能会发生RII 或RESI.由于重碰撞过程的存在,NSDI 中两个电子的行为存在关联性,对此人们进行了大量的理论和实验研究[24,25].早期,NSDI 经常发生在线偏振激光场驱动原子的情况下,而对于椭圆偏振激光场和圆偏振激光场,由于旋转的电场会带来横向的漂移速度,使返回电子远离母离子,进而阻止了重碰撞过程[26,27].所以研究主要集中于线偏振激光场和平行双色激光场来驱动NSDI.近年来,由两个不同频率的圆偏振激光场组成的双色圆偏振激光场(two-color circularly polarized,TCCP)得到了广泛关注[28,29],由于其具有特殊的电场结构和更多的可调参数,故对TCCP 激光场的研究成为热点之一[30-33].其中,Eichmann等[34]在实验上验证TCCP激光场驱动高次谐波的发射.随后,Li等[35]发现反旋TCCP 激光场有助于提高O2分子NSDI 的产量.Peng 和Bai[36]也发现了反旋TCCP 激光场中存在与线偏振激光场中相似的标度定律.然而,由于反旋TCCP 激光场具有空间对称性,返回电子可以从多个方向返回母离子,因此不利于对重碰撞过程的理解[37].而反旋双色椭圆偏振(two-color elliptically polarized,TCEP)激光场打破了这种对称性,所以可以预测电子行为在反旋TCEP 激光场中与在反旋TCCP 激光场中会有较大的不同[38].最近,很多工作聚焦于在TCEP 激光场中研究高次谐波的产生和阈上电离,并且,现在对于反旋TCEP 激光场中NSDI 的研究也正在如火如荼的进行[37-41].

本文采用经典系综方法研究了反旋TCEP 激光场中Ar 原子的NSDI,其中,反旋TCEP 激光场由两个相同椭偏率的椭圆偏振激光场组成.研究表明,由于反旋TCEP 激光场不具有空间对称性,返回电子主要从一个方向返回母离子,从而导致电子的动量分布表现出很强的不对称性[37].并且随着椭偏率的增大,Ar 原子NSDI 的产量逐渐减小,电子对主要的关联特性也从正相关逐渐演变成反相关.此外,椭偏率和旅行时间都影响着重碰撞时刻电子动量的分布形式,也就是两者都会影响两个电子的发射方向.

2 理论方法

本文采用基于Eberly 提出的经典系综方法[42,43],这种方法得到的NSDI 结果与许多实验观察到的现象十分吻合[44,45].Ar 原子的哈密顿量可以写为(除特殊说明,文中物理量均采用原子单位)

式中,He是无外加激光场时,Ar 原子的总能量(第1 电离能与第2 电离能之和);ri和pi代表两个电子的位置和动量;是电子与母离子之间的库仑势;Vee(r1,r2)=是电子与电子之间的库仑势.这里设置软核参数a(a=1.5)和b(b=0.05),其中,a是为了使体系更加稳定,避免电子发生自电离,b是为了使结果更加接近电子间的相互作用,避免物理奇点的产生.Ar 原子在外部激光场中的哈密顿量表示为

本文使用的组合激光场为E(t)=E800(t)+E400(t),其中E800(t)和E400(t) 分别为波长为800 nm (ω800=0.057)和400 nm (ω400=0.114)的椭圆偏振激光场.两个椭圆偏振激光场表示为

其中,x和y分别为x方向和y方向上的单位向量;E0是组合激光场的振幅;ε为两个椭圆偏振激光场的椭偏率;γE=1,表示两个椭圆偏振激光场的振幅相同;f(t)=sin2(πt/NT) 是脉冲包络函数,T是光学周期(o.c.),N为光学周期数,本文中取N=16.在我们的计算中,两个电子的运动由哈密顿正则方程组求解:

方程(5)可以通过4—5 阶龙格库塔算法求解.两个电子的初始位置和动量都满足高斯分布,确保总能量为正.为了得到初始系综,我们让电子自由演化足够长的时间(100 a.u.),使电子的位置和动量保持稳定.之后加入外部激光场,所有的电子在外部激光场的作用下开始演化,直至激光脉冲结束.若两个电子的能量在脉冲结束时都大于0,则记录为一次双电离事件[46].

3 结果与讨论

本文通过数值模拟得到了不同椭偏率下反旋TCEP 激光场的电场E(t) 和负矢势曲线-A(t),如图1(a)—(d)所示,其中横轴和纵轴分别表示反旋TCEP 激光场的电场E(t) 和负矢势-A(t) 在椭圆偏振激光场长轴方向(x方向)上的分量和在椭圆偏振激光场短轴方向(y方向)上的分量.可以看到随着椭偏率的增大,电场形状和负矢势的形状越来越符合三叶草状结构和三角形状结构,这是因为反旋TCEP 激光场是由两个椭圆偏振激光场组合而成.与之前的反旋TCCP 激光场不同的是,反旋TCEP 激光场每个波瓣幅值和波瓣之间的夹角不再相同[30-32,35,47].图1(e)为Ar 原子在不同椭偏率的反旋TCEP 激光场下,双电离(double ionization,DI)产量随激光强度的变化曲线,其中横轴表示激光强度,纵轴表示双电离产量.而在图1(e)中可以清楚观察到较为明显的“膝盖”结构,这说明在反旋TCEP 激光场中存在NSDI 现象.并且可以发现NSDI 依赖于椭偏率,随着椭偏率的增大,Ar 原子NSDI 的产量逐渐减小.考虑到反旋TCEP 激光场不同于反旋TCCP 激光场具有空间对称性,因此,返回电子主要从一个方向返回母离子[37],这是因为随着椭偏率的增大,在返回电子返回母离子方向上的电场强度会减弱,进而造成其重碰撞事件发生的概率减小,所以其NSDI 的产量也会逐渐减小.为了较好地研究Ar 原子在不同椭偏率下反旋TCEP 激光场中的NSDI,在“膝盖”结构所对应激光强度的范围内,选取I0=4×1014W/cm2的激光强度.

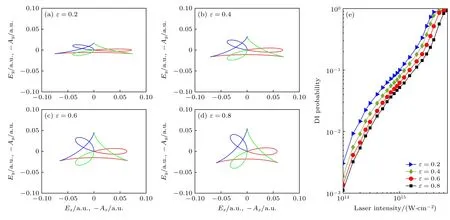
图1 (a)—(d)不同椭偏率下,反旋TCEP 激光场的电场结构和负矢势曲线,三瓣代表电场结构,三角形代表反旋TCEP 激光场的负矢势;(e)对于不同椭偏率的反旋TCEP 激光场下,Ar 原子随激光强度变化的双电离产量曲线Fig.1.(a)-(d) Electric field structure and negative vector potential curve of counter-rotating TCEP laser fields for different ellipticities.The three lobes represent the electric field structure,and the triangle structure represents the negative vector potential of the counter-rotating TCEP laser field.(e) The yield of NSDI for Ar as a function of laser intensity in counter-rotating TCEP laser fields for different ellipticities.

图2 给出了反旋TCEP 激光场中不同椭偏率下两个电子的动量分布,其中横轴表示两个电子沿x方向上的动量分量,纵轴表示两个电子沿y方向上的动量分量.在simple-man 模型中,由于忽略了库仑势和初始动量的影响,两个电子的末态动量应与负矢势-A(t) 曲线分布相同[18].但在图2中,我们可以发现随着椭偏率的增大,电子动量分布越来越趋近于三角形,并且电子动量主要分布在第四象限,这是因为反旋TCEP 激光场不具有空间对称性,返回电子主要从一个方向返回母离子导致的[37].

图2 不同椭偏率的反旋TCEP 激光场中电子动量分布(实线为反旋TCEP 激光场的负矢势-A(t))(a) ε=0.2;(b) ε=0.4 ;(c) ε=0.6;(d)ε=0.8Fig.2.Momentum distributions at different ellipticities in counter-rotating TCEP laser fields: (a) ε=0.2;(b) ε=0.4;(c)ε=0.6;(d) ε=0.8.The solid line represents the negative vector potential-A(t) of counter-rotating TCEP laser fields.

为了解释反旋TCEP 激光场中NSDI 的产量对椭偏率的依赖,向后跟踪了经典的NSDI 轨迹并做了统计分析.通过追踪经典轨迹,可以确定每个NSDI 事件的单电离时刻(tSI)和重碰撞时刻(tRC).在这里,单电离时刻定义为Ar 原子中某个电子首次能量为正的时刻,重碰撞时刻定义为单电离后两个电子最接近的时刻.图3 统计了NSDI 事件中所有发生单电离和重碰撞的电子数量,并且给出了在反旋TCEP 激光场中Ar 原子单电离时刻和重碰撞时刻的统计分布.在图3(a)—(d)中横轴表示单电离时刻,纵轴表示发生单电离的电子数量,在图3(e)—(h)中横轴表示重碰撞时刻,纵轴表示发生重碰撞的电子数量.从图3 可以发现,随着椭偏率的增大,单电离时刻和重碰撞时刻的峰值所在的时刻并没有发生变化,但是它们峰值的电子数量在逐渐降低.这与图1(e)所展示的现象正好吻合,由于单电离产量和重碰撞产量的降低,所以其NSDI 的产量随着椭偏率的增大而减少,NSDI 依赖于椭偏率.

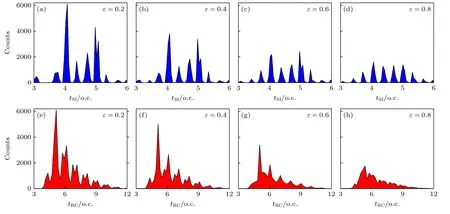
图3 (a)—(d)不同椭偏率下,Ar 原子单电离时刻 tSI 的分布;(e)—(h)不同椭偏率下,Ar 原子重碰撞时刻 tRC 的分布Fig.3.(a)-(d) Statistical distribution of the single ionization time tSI for Ar atoms with different ellipticities;(e)-(h) statistical distribution of the electron recollision time tRC for Ar atoms with different ellipticities.

NSDI 过程的重要意义之一就是探究两个电子的关联特性.由于重碰撞过程的存在,返回电子会传递能量给束缚电子,两个电子的动量会产生关联.如果返回电子与束缚电子发生重碰撞时的能量较大,束缚电子会通过RII 机制发生电离,导致关联电子动量分布主要在第一和第三象限,这时返回电子和束缚电子的关联特性是正相关.而如果返回电子与束缚电子发生重碰撞时的能量较小,束缚电子会通过RESI 机制发生电离,导致关联电子动量分布主要在第二和第四象限,这时返回电子和束缚电子的关联特性是反相关.因此,图4(a)—(d)给出了两个电子在x方向上的关联电子动量分布,其中横轴表示返回电子在x方向上的动量分量,纵轴表示束缚电子在x方向上的动量分量.同时在图4(e)—(h)中给出了两个电子在y方向上的关联电子动量分布,其中横轴表示返回电子在y方向上的动量分量,纵轴表示束缚电子在y方向上的动量分量.

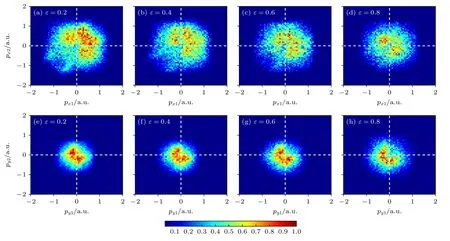
图4 (a)—(d)不同椭偏率下,两个电子在x 方向上的关联电子动量分布;(e)—(h)不同椭偏率下,两个电子在y 方向上的关联电子动量分布Fig.4.(a)-(d) Correlated momentum distributions of the electrons in the x direction for different ellipticities;(e)-(h) correlated momentum distributions of the electrons in the y direction for different ellipticities.

从图4(e)—(h)可以看到,两个电子的动量主要分布在原点附近,其电子动量比较小,并且变化不大.而从图4(a)—(d)可以看到,两个电子的动量较大,且变化明显,因此两个电子总的关联特性主要依赖于x方向上的电子动量.现在我们主要关注x方向上的关联电子动量分布.当椭偏率ε=0.2时,关联电子动量分布主要在第一、第二和第四象限,其中第一和第三象限的关联电子动量分布略多于第二和第四象限的关联电子动量分布,NSDI 中正相关的比例约为51.1%,整体呈现出正相关特性.对于椭偏率ε=0.4,第一象限的关联电子动量分布开始减少,但是关联电子动量分布仍然主要在第一、第二和第四象限,NSDI 中正相关的比例降低到50.1%.当椭偏率进一步增大到ε=0.6 时,第二和第四象限的关联电子动量分布开始略多于第一和第三象限的关联电子动量分布,NSDI 中反相关的比例约为51.2%.当椭偏率ε=0.8 时,关联电子动量分布主要在第二和第四象限,其中NSDI 中反相关的比例约为52.0%,此时整体呈现出反相关特性.由此可以看出,随着椭偏率的增大,电子对的关联特性由正相关逐渐演化为反相关.

为了解释不同椭偏率的反旋TCEP 激光场中两个电子的关联特性,图5 给出了在反旋TCEP激光场中Ar 原子旅行时间(tRC-tSI)、返回电子重碰撞能量和延迟时间(tDI-tRC)的统计分布.图5(a)—(d)中的横轴表示旅行时间,纵轴表示旅行时间的概率,图5(e)—(h)中的横轴表示返回电子的重碰撞能量,纵轴表示返回电子重碰撞能量的概率,图5(i)—(l)中的横轴表示延迟时间,纵轴表示延迟时间的概率.旅行时间是重碰撞时刻和单电离时刻之间的时间间隔,返回电子重碰撞能量是指返回电子与束缚电子发生重碰撞时的能量,延迟时间是双电离时刻和重碰撞时刻之间的时间间隔[16,48].

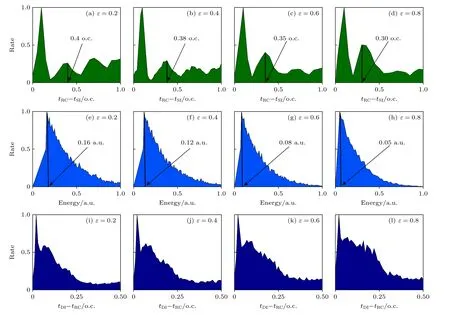
图5 (a)—(d)不同椭偏率下,Ar 原子旅行时间( tRC-tSI)的分布;(e)—(h)不同椭偏率下,返回电子重碰撞能量的分布;(i)—(l)不同椭偏率下,Ar 原子延迟时间( tDI-tRC)的分布Fig.5.(a)-(d) Statistical distribution of the traveling time ( tRC-tSI) for Ar atoms with different ellipticities;(e)-(h) distributions of the returning electron recollision energy with different ellipticities;(i)-(l) statistical distribution of the delay time(tDI-tRC) for Ar atoms with different ellipticities.

从图5(a)—(d)可以看到,对于旅行时间,主要的峰值大约在0.1 o.c.这表明返回电子在很短的时间内与母离子发生碰撞.并且随着椭偏率的增大,第2 个峰的概率在逐渐增大,其所对应的旅行时间也从0.4 o.c.减小到了0.3 o.c.,也就是逐渐向左平移.这意味着在反旋TCEP 激光场中,越来越多返回电子的轨迹变短.在图5(e)—(h)中,可以看到返回电子在重碰撞时的能量分布,并且随着椭偏率的增大,返回电子重碰撞能量分布峰值处的能量从0.16 a.u.减小到了0.05 a.u.,这表明返回电子的重碰撞能量在变低,并且返回电子的碰撞不足以使束缚电子电离,最终返回电子和束缚电子在激光场的作用下在不同的时刻电离,这也就导致其出射方向的不同.因此,更多的电子对表现出反相关特性.在图5(i)—(l)中,延迟时间主要的峰值大约在0.02 o.c.这表明返回电子在与束缚电子发生碰撞后,束缚电子以极短的时间出射,其电离机制主要是RII.并且随着椭偏率的增大,可以发现延迟时间在0.04—0.3 o.c.之间的概率在增大.这表明越来越多的束缚电子以RESI 机制出射.此结果表明,随着椭偏率的增大,越来越多的束缚电子以较长的延迟时间电离,两个电子更倾向于向相反的方向出射.同样,这也表明更多的电子对表现出反相关特性.

为了更加深入地理解不同椭偏率下反旋TCEP激光场中Ar 原子的NSDI,计算了相应椭偏率下电子的运动轨迹,如图6 所示,其中横轴为两个电子在x方向上的坐标,纵轴为两个电子在y方向上的坐标.图6(a)—(d)为“短轨迹”(tRC-tSI＜0.2 o.c.),图6(e)—(h)为“长轨迹”(tRC-tSI≥0.2 o.c.),并且蓝色实线代表返回电子,红色虚线代表束缚电子.从图6(a)—(d)可以发现,当椭偏率较小的时候,返回电子以一种不规则形状的轨迹返回母离子,随着椭偏率的增大,“短轨迹”的形状越来越接近于三角形.在图6(e)—(h)中,返回电子在最初返回母离子的过程中没有与母离子发生碰撞,而是在返回过程中围绕母离子多次旋转,最终产生了一次碰撞,并且随着椭偏率的增大,“长轨迹”的形状也同样越来越接近于三角形.此结果表明,椭偏率的增大会使“短轨迹”和“长轨迹”的形状越来越接近于三角形,这是因为其负矢势形状越来越符合三角形结构.

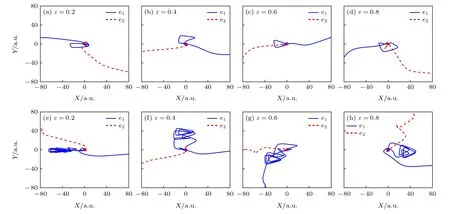
图6 不同椭偏率的反旋TCEP 激光场中两个电子轨迹(a)—(d) 上面一行是“短轨迹”( tRC-tSI ＜0.2 o.c.)的电子轨迹;(e)—(h)下面一行是“长轨迹”( tRC-tSI ≥0.2 o.c.)的电子轨迹Fig.6.Trajectory of the two electrons at different ellipticities in counter-rotating TCEP laser fields: (a)-(d) The top row shows trajectories of the ionized electron coming back to the parent ion core with the “short trajectory” ( tRC-tSI ＜0.2 o.c.);(e)-(h) the bottom row shows trajectories of the ionized electron coming back to the parent ion core with the “long trajectory”(tRC-tSI ≥0.2 o.c.).

图7 是不同椭偏率的反旋TCEP 激光场中两个电子在x方向上的关联电子动量分布,其中横轴为返回电子在x方向上的动量分量,纵轴为束缚电子在x方向上的动量分量.图7(a)—(d)为“短轨迹”(tRC-tSI＜0.2 o.c.)的关联电子动量分布,图7(e)—(h)为“长轨迹”(tRC-tSI≥0.2 o.c.)的关联电子动量分布.在图7(a)—(d)中,当椭偏率ε=0.2时,关联电子动量分布主要在第一象限,其中,NSDI 中正相关比例为55.3%,整体表现出正相关特性.对于椭偏率ε=0.4 时,关联电子动量分布主要在第一、第二和第四象限,其中第一和第三象限的关联电子动量分布略多于第二和第四象限的关联电子动量分布,此时NSDI 中正相关的比例约为51.7%.而当椭偏率进一步增大到ε=0.6和ε=0.8时,关联电子动量分布主要在第二和第四象限,其中NSDI 中反相关比例为51.1%和52.2%.然而在图7(e)—(h)中,当椭偏率ε=0.2 时,关联电子动量分布主要在第一、第二和第四象限,其中NSDI 中正相关的比例约为50.1%.而当椭偏率ε=0.4时,第二和第四象限的关联电子动量分布开始增加,此时NSDI 中反相关的比例约为50.4%.对于椭偏率ε=0.6和ε=0.8 时,关联电子动量分布主要在第二和第四象限,此时NSDI 中反相关的比例为51.2%和52.0%.这表明随着椭偏率的增大,无论“短轨迹”还是“长轨迹”,电子对的关联特性都是由正相关逐渐演化为反相关,并且两个电子的出射方向也从同向出射向反向出射转变.综上所述,椭偏率和旅行时间不仅会影响电子对的关联特性,也会对电子的出射方向产生影响.

图7 不同椭偏率下,两个电子在x 方向上的关联电子动量分布(a)—(d)上面一行是“短轨迹”( tRC-tSI ＜0.2 o.c.)的关联电子动量分布;(e)—(h)下面一行是“长轨迹”( tRC-tSI ≥0.2 o.c.)的关联电子动量分布Fig.7.Correlated momentum distributions of the electrons in the x direction for different ellipticities: (a)-(d) The top row shows correlated momentum distributions with the “short trajectory” ( tRC-tSI ＜0.2 o.c.);(e)-(h) the bottom row shows correlated momentum distributions with the “long trajectory”( tRC-tSI ≥0.2 o.c.).

4 结论

本文使用经典系综方法研究了反旋TCEP 激光场中Ar 原子的NSDI.研究结果表明,反旋TCEP 激光场呈现出不对称的三瓣结构,并且NSDI的产量与激光强度的变化曲线表现出标志性的“膝盖”结构.由于反旋TCEP 激光场的不对称性,导致其返回电子主要从一个方向返回母离子,电子的动量分布也不具有对称性.通过对NSDI 中单电离时刻和重碰撞时刻分析发现,随着椭偏率的增大,其单电离产量和重碰撞产量逐渐减少,导致了其NSDI 的产量也逐渐减少.本文还讨论了NSDI 中两个电子的关联特性,当椭偏率较小的时候,整体呈现出正相关特性,然而随着椭偏率的增大,电子对的关联特性由正相关逐渐演化为反相关,并且旅行时间和返回电子的重碰撞能量在逐渐减小,延迟时间反而在增大,导致了更多的束缚电子以RESI机制出射,这是电子对关联特性发生变化的主要原因.除此之外,还通过x方向上的关联电子动量分布发现,无论是“短轨迹”还是“长轨迹”,椭偏率的增大会使电子对的关联特性由正相关演变为反相关,也同样会使两个电子由同向出射转变为反向出射,这表明椭偏率和旅行时间不仅会影响电子对的关联特性,也会对电子的出射方向有影响.本文进一步完善了反旋TCEP 激光场中NSDI 的研究,并为实验中研究电子的关联特性提供了参考.