岩石单结构面剪切变形渗透性演化规律

常江 姜克儒 马海春 于智敏

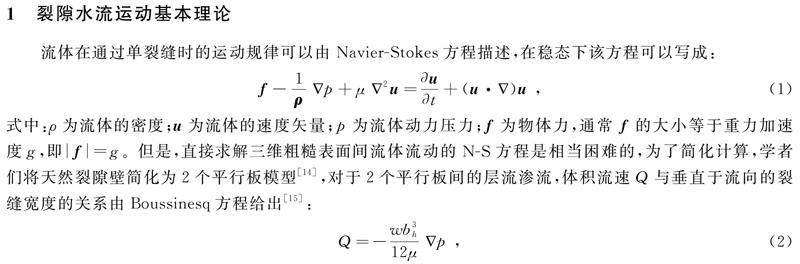
摘 要：為了研究剪切作用下单裂隙渗透性的演化规律，在Comsol中采用Weierstrass随机分形函数来生成单裂隙，调整2个裂隙面的相对位移来模拟剪切作用，通过分析不同剪切位移条件下裂隙隙宽的变化以及不同流量下的非线性效应发生的界定范围，并绘制散点图与函数曲线拟合确定剪切过程影响裂隙渗透率的因素，给出定量关系。结果表明：未发生剪切时，隙宽的概率密度分布满足标准的高斯分布，而随着剪切过程的发生，隙宽的高斯分布被破坏，仅体现标准高斯分布的部分特征；发生剪切时，渗透率先有一个减小的过程，然后在一定范围内波动;当Re>9.6时，流体开始从线性向非线性发展。对岩石单结构面剪切变形过程中裂隙孔径变化对流体渗流特性的影响进行模拟，可为分析地质体中结构面变形对地热变化的影响提供参考。

关键词：渗流力学；单结构面；剪切变形；数值模拟；渗透率；Forchheimer公式

中图分类号：P641.2；TU452   文献标识码：A   文章编号：1008-1542（2024）02-0207-10

Seepage evolution of shear deformation for a single rock structure surface

CHANG Jiang1， JIANG Keru1， MA Haichun2，3， YU Zhimin2

（1.State Grid Economic and Technology Research Institute of Anhui Electric Power Company Limited， Hefei， Anhui 230061， China;2.School of Resources and Environmental Engineering， Hefei University of Technology，Hefei， Anhui 230009， China;3.Hydraulic Fracturing and Oil-Gas Migration Development Center， Hefei University of Technology， Hefei， Anhui 230009， China）

Abstract：In order to study the evolution of fracture permeability under shear action， a Weierstrass random fractal function was used in Comsol to generate a single fracture， and the relative displacements of two fracture surfaces were adjusted to simulate shear action. Changes of fracture width under different shear displacements and the defined range of nonlinear effects under different flow rates were analyzed， the factors affecting fracture permeability in shear process were determined by using scatter plot and function curve fitting， and the quantitative relationship was given. The results show that the probability density distribution of the gap width meets the standard Gaussian distribution without shearing， but with the shearing process， the Gaussian distribution of the gap width is destroyed and only reflects parts of the characteristics of the standard Gaussian distribution. When the shear occurs， the permeability first has a decreasing process， and then fluctuate within a certain range. The smaller aperture is unfavorable to the water flow through near the contact area. When Re>9.6， the fluid begins to develop from linear to nonlinear. The influence of fracture aperture on fluid seepage characteristics during shear deformation of single fracture of rock is simulated， which provides some reference for analyzing the geothermal change caused by fracture deformation in geological bodies.

Keywords：seepage mechanics; single structure surface; shear deformation; numerical simulation; permeability; Forchheimer formula

表面几何形状及其在剪切过程中的演化对岩石间断裂的流体力学行为的影响一直是地质学家面临的重要问题。在剪切过程中，只有一小部分不连续点在接触，并且这些接触点上的实际应力远远大于名义应力。然而，在剪切过程中测量接触面积一直是重大的实验挑战，因为难以监测剪切过程中表面的演化。地层断裂的水力学行为主要由预先存在的不连续点（断层和断裂）的性质控制[1]。了解岩石不连续体对不同应力条件的流体渗流，具有广泛的工程地质应用，如边坡和大坝稳定性、自然断层地震成核、水库工程、长期放射性废物处置、二氧化碳地质封存和地热资源分布变化等。对与不连续点相交的地质结构失效的评估需要详细分析不连续点的抗剪强度特性[2]，表面粗糙度作为影响岩石不连续体水力学行为的主要参数之一，在过去几十年里受到了广泛关注，量化岩石表面粗糙度的参数有很多，如表面粗糙度均方根Z2、分形维数D、表面粗糙度参数Rs和粗糙度轮廓指数Rp，其中应用最广泛的参数是BARTON等［3］提出的节理粗糙度系数 （JRC）法，通过将JRC与隙宽结合提出了一个可以合理预测水力开度的公式，但对该过剪切过程中粗糙度变化所造成的地下水渗流变化理论成果是相当有限的[4-7]。

沿不连续界面形成的实际接触面积远低于界面的标称面积，即使是平面和平面不连续界面。只有实际接触区域负责摩擦响应，而施加的应力不能通过空隙空间传递[8-9]。因此，作用于表面接触点的实际应力可能比作用于标称表面的应力大几个数量级[10-11]。岩体不连续性是低渗透性地层中流体流动的主要通道，也是地热资源的广泛分布和交换位置。受外力作用影响，2个表面之间的接触面积和相应的空隙空间发生变化，导致断裂岩石的水力特性发生改变[12-13]。

本文结合单结构面剪切变形对裂隙的孔径分布规律进行了分析，在不同的接触位置变化下渗流流态均是层流，呈现非线性流，压力梯度-▽P和出口流量Q呈二次函数变化关系，可以使用Forchheimer公式进行拟合。

1 裂隙水流运动基本理论

流体在通过单裂缝时的运动规律可以由Navier-Stokes方程描述，在稳态下该方程可以写成：

f-1ρSymbolQC@p+μSymbolQC@2u=ut+（u·SymbolQC@）u ，（1）

式中：ρ為流体的密度；u为流体的速度矢量；p为流体动力压力；f为物体力，通常f的大小等于重力加速度g，即|f|=g。但是，直接求解三维粗糙表面间流体流动的N-S方程是相当困难的，为了简化计算，学者们将天然裂隙壁简化为2个平行板模型[14]，对于2个平行板间的层流渗流，体积流速Q与垂直于流向的裂缝宽度的关系由Boussinesq方程给出[15]：

Q=-wb3h12μSymbolQC@p  ，（2）

式中：Q为流量，m3/s；bh为等效水力隙宽，m；-SymbolQC@p为压力梯度的大小，Pa/m，SymbolQC@p=dp/dx；w为裂隙的宽度，m，在三维模型中，w取垂直于流体流动方向的宽度。式（2）为计算单裂隙或裂隙网络内的流体流动的立方定律公式。由表达式可知，流量Q与压力梯度的大小-SymbolQC@p线性相关，与等效水力隙宽bh的三次方呈正比。

当流速较小、惯性力的影响可近似忽略时，裂隙中的水流属于线性流，即黏滞力发挥主要作用。在水流速度增大时，流量和压力梯度不再呈线性关系[16]，非线性的弱惯性效应开始显现，流速继续增大，过渡到强惯性效应，惯性力的影响不可忽视，立方定律不再适用，描述非线性流的Forchheimer方程表述方式如下[17]：

-▽p=AQ+BQ2 ，（3）

式中：A和B为系数，与结构面几何特性、水流运动参数等有关；Q为黏滞力的影响；Q2为惯性力的影响。

2 单裂隙剪切渗流模型

2.1 模拟基于的前提和假设

1）研究表明，在高地应力条件下，单裂隙的剪切过程存在平移剪切，即法向压力远远大于剪应力，结构面发生的变形可近似忽略[18]。故模型可以简化为形态结构稳定的上下结构面发生相对运动（见图1），选取剪切过程中的几个位移状态进行研究，d代表剪切位移量。

2）本研究忽略了剪切过程的磨损以及渗流压力对岩石作用带来的影响，主要是通过对上下结构面施加相对位移使裂隙的几何形态发生变化，如隙宽、粗糙度、接触面积等，从而引起流体在裂隙中渗流特性发生变化。

3）研究对象为上下水平岩体中间的水平单裂隙，无任何角度的倾斜。

4）流体设置为水，所有物理参数的选取均以水为参考。

2.2 物理模型与数学模型

HUANG 等[19]通过建立三维粗糙裂隙模型，探究渗流方向、粗糙度、剪切位移等因素对流动特性和渗透性的影响，LIU等[20]通过数值方法生成大量粗糙表面，并模拟了裂隙面的渗流剪切过程。本研究采用Weierstrass随机分形函数来生成水平裂隙上下结构面的角点坐标，具体表达式如下：

zij（xi，yi）=∑∞k=1Ckλ-（3-D）ksin［λk（xicos Bk+yisin Bk）+Ak］，（4）

式中：zij （xi，yi）为结构面上平面位置（xi，yi）的角点坐标；Ck为服从标准正态分布的相互独立的随机数；D，λ为分形变量；Ak和Bk为在[0，2π]上服从均匀分布的相互独立的随机数；i，j为角点在平面上投影位置的标号；k为随机数的个数，本文取150；xi，yi为对应x，y轴的坐标。

将Weierstrass随机分形函数计算得到的上、下裂隙面散点数据以 .[KG-*3]txt格式导入COMSOL中，经过插值处理再通过拉伸和扫掠等几何操作，得到如图2所示的上下盘岩体模型。

其中上下两盘岩体沿x方向长度为50 mm，沿y方向长度为20 mm，中间的缝隙即为模拟的裂隙。选取30 mm×20 mm的裂隙区域作为研究范围（如图2中紫色区域所示）。

COMSOL在进行裂隙渗流仿真时，首先要考虑的是流体类型，不同的流体具有不同的性质，参数的取值也不同。其次还要考虑四面体网格的剖分精度，权衡计算精度与计算效率等问题。COMSOL在模拟地下水层流运动时分为稳态和瞬态2种模型，本模型类型设置为稳态，通过求解黏性不可压缩流体动量守恒的运动方程（N-SEquations）得到裂隙水流基本物理参量，在直角坐标系中N-S方程的分量形式如下：

ρut+uux+vuy+wuz=ρfx-px+μ2ux2+2uy2+2uz2，ρvt+uvx+vvy+wvz=ρfy-py+μ2vx2+2vy2+2vz2，ρwt+uwx+vwy+wwz=ρfz-pz+μ2wx2+2wy2+2wz2，（5）

式中：ρ为流体密度，kg/m3；u，v，w为流体在t时刻、点（x，y，z）处的速度分量，m/s；p为压强，Pa；f为单位体积流体受的外力，N；μ是流体动力黏度，Pa·s。

图3所示为裂隙模型研究范围及边界条件设置，其中边界条件如下：

q|Γn=0 ，（6）

式中Γn代表除去入口和出口的所有边界，式（6）表示Γn均为零流量边界。

初始条件如下：

vs|Γ1=vi，  t=0，psΓ2=0，  t=0，（7）

式中：Γ1为入口边界；Γ2为出口边界；vs为入口处初始速度设定值，取值为0.05～0.40 m/s，间隔0.05，共8个速度值，该范围相对于试验测试的范围更宽，便于充分考察线性和非线性渗流特征；i=1，2，…，8，代表每次的注水次数；初始时出口为自由边界，压强为0。

通过求解COMSOL中自带的N-S方程得到裂隙内的三维流场分布。本文采用COMSOL中的层流模块，用常规四面体对模型进行划分，采用的网格剖分精度为较细化。以剪切位移6 mm的模型为例，四面体网格剖分后生成126 386个单元。对于不可压缩流体，针对非线性流动的Forchheimer方程和线性流动的渗透率计算公式可以分别写为

-▽p=AQ+BQ2=μkvυ+ρkiυ2 ， （8）

k=-μQSSymbolQC@p，（9）

式中：Q为出口流量，m3/s；A为线性项系数，Pa·s·10-4；B為非线性项系数，即惯性系数，×10-4 Pa·s；kv为黏性渗透率，m2；ki为惯性渗透率，m2；υ为体积通量，m/s；μ为动力黏度，Pa·s；k为裂隙渗透率，m2；S为试样横截面面积，m2。

对于裂隙流，可对雷诺数Re进行如下定义：

Re=ρQLμ， （10）

式中L为裂隙沿压力梯度方向的长度，m。

本文中流体设置为水，动力黏度μ取0.001；出口流量Q取出口流速与出口面积的乘积；S取等效水力隙宽bh与w的乘积；▽p取出入口间的压力差Δp与裂隙长度L的比值。

3 剪切渗流结果分析与讨论

3.1 隙宽b（x，y）

为了检验建立的裂隙模型是否可以和实际裂隙很好近似，以及剪切过程对隙宽函数b（x，y）值的分布情况的影响，计算了各剪切状态研究区域的隙宽值，并绘制了二维分布图（见图4），右图蓝色颜色越深代表该处隙宽值越小，反之则越大，而白色区域则显示隙宽为0 mm，表明该处上下裂隙面已经闭合。隙宽大小分布情况与左图所示的接触区域也基本可以形成对应，证明计算结果无较大偏差。

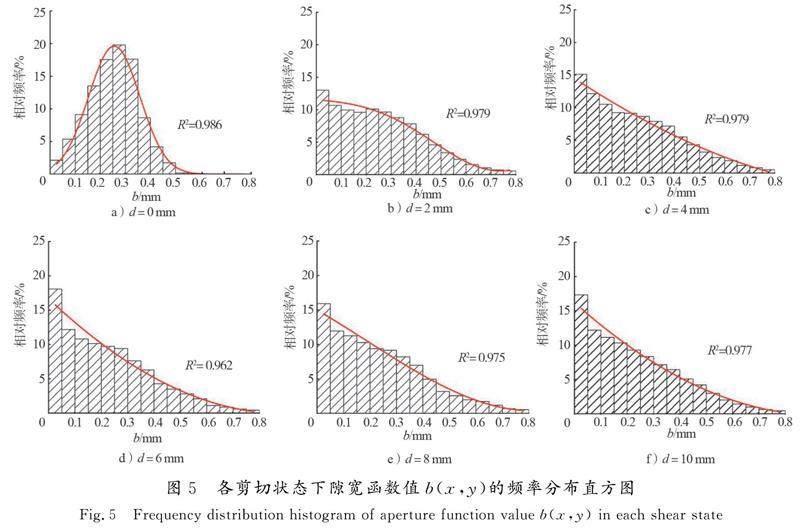
关于裂隙的诸多研究表明[21-22]，裂隙的隙宽函数值b（x，y）基本满足高斯分布规律，即在频率分布直方图上呈现中间高、两边低的钟形曲线分布，统计各剪切状态计算所得隙宽值，绘制频率分布直方图，如图5所示。

从图5可以看出：未发生剪切时隙宽的频率分布符合完整的高斯分布，平均隙宽值附近出现的频率较高，这也证明了Weierstrass随机分形函数的合理性;随着剪切过程的进行，小隙宽（0.1 mm以下）出现的频率增大，相比于未发生剪切状态（d=0 mm），当剪切位移为10 mm时，小隙宽相对频率增加约20%;平均隙宽（0.3 mm）以下的数量大于平均隙宽以上的数量，不再符合完整的高斯分布形式。

3.2 水流性质

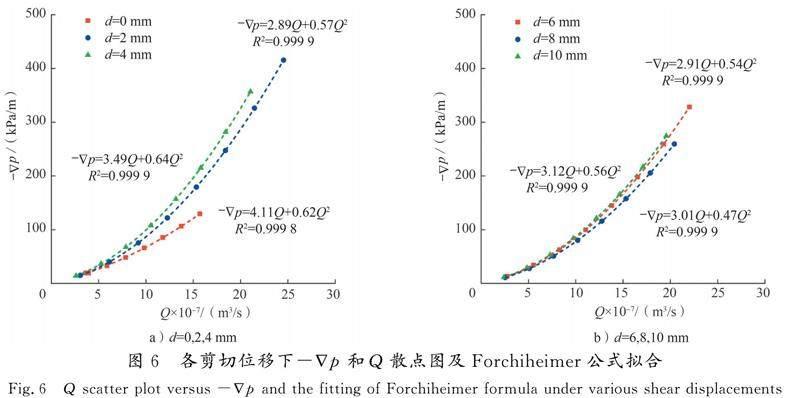
不同剪切位移下压力梯度的大小-▽p和出口流量Q的关系如图6所示。由散点的分布情况可知，随着流量Q的增加，-▽p以非线性的形式增长，对散点图进行二次函数拟合，相关系数R2与1非常接近。这说明通过求解Navier-Stokes方程得到的-▽p与Q的关系，同样也可使用Forchheimer方程进行描述。流动的雷诺数已被广泛用于量化流动系统中惯性效应的预期影响程度[23]。BEAR［24］认为，当雷诺数Re>1时，流动变为非层流（非达西式），但当雷诺数Re= 1～10时，一种过渡流动形式（可能表现出达西式行为的某些方面）占主导地位。这与本文实验结果一致，如图7所示。

当Re<9.6时，Forchheimer公式与Darcy公式基本吻合，此时层流占据了主导地位；随着出口流量Q的增加，即Re>9.6时，抛物线的弯曲程度增大，在出口流量增长至20×10-7 m3/s时，压力梯度-▽p随着增加了约200 kPa/m。二者的非线性关系更加明显，也就是BQ2/AQ不断增大，裂隙水流的非线性特征越来越明显，惯性力的影响逐渐增强[25-28]，此时Forchheimer公式逐渐偏离Darcy公式，裂隙中的流体开始向着紊流方向发展。

3.3  剪切对渗透性影响

各剪切位移、不同入口速度条件下，渗透率k与剪切位移d的关系如图8所示。入口流速一定时，渗透率在一定范围内波动变化。纵向来看，随着入口流速的增加，渗透率呈现减小的趋势，当入口流速从0.05 m/s增长至0.4 m/s时，渗透率也随之增加2×10-9 m2，这表明裂隙入口处的水流速度可以改变裂隙渗透率的计算结果；整体来看，不同入口流速下剪切过程渗透率变化趋势基本一致，不同折线间基本无交点。值得注意的是，在同一剪切位移状态下，随着入口流速的增加，渗透率的差异是在逐渐减小的，如图8中红色虚线矩形所示，折线间距依次减小。当剪切位移距离为10 mm、入口流速从0.05 m/s 增加到0.1 m/s时，渗透率增加了约0.3×10-9 m2，而此时同一状态下入口流速若从0.35 m/s增长至0.4 m/s 时，渗透率仅增加了0.1×10-9 m2。

1）沿x轴方向在y轴的中间位置依次截取裂隙研究区域，如图9所示，计算截面处上下边界的高度差，绘制曲线如图10所示。

从图10可以看出，初始状态截面处隙宽分布均匀，随后的剪切过程隙宽分布均呈现明显的不均匀性，曲线起伏波动较大。由图11可知，上下结构面接触区域的增加也会使绕流现象增多。初始剪切状态压力分布变化也反映出水流的不规则流动。压力梯度由均匀分布逐渐过渡至不规则分布，在入口流速均设置为0.2 m/s的条件下，由比例尺刻度可知，入口最大水压有增大的变化过程，当剪切距离增加至2 mm时，最大压力增加了3.4×103  Pa，说明水流通过裂隙的阻力增加，初始剪切阶段渗透性能是减小的。

由图12可知：未发生剪切时，整体流线保持相对平行，流速相对均匀，流线只在裂隙起伏较大的位置发生变化；发生剪切后，由于接触区阻碍了流体的流动，流体会绕过接触区继续流动，绕流增多，流线在接触区域附近弯曲和偏转。结合隙宽分布图发现，剪切作用发生后，小隙宽所占比例增加（深色区域占比增多），因此流动的孔径变窄，可供流体流动的面积变小，导致整体的流线分布不均。

绘制剪切位移下的渗透率k與入口实际流速ve散点图，如图13所示（以d=2 mm为例）。结果表明，渗透率随着入口实际流速增加呈现非线性减小，入口实际流速从0.1 m/s增加至0.3 m/s 时，渗透率降低了约1.4×10-9m2。为了研究渗透率与入口实际流速之间的关系，采用二次函数和幂函数模型进行最佳拟合回归分析，2种函数拟合程度如表1所示，可以发现二次函数的相关拟合系数R2更接近于1，表明二次函数拟合更为准确，这说明Forchheimer方程（二次函数）可以更好地表达剪切状态下裂隙渗流规律。

4 结 语

基于单裂隙几何模型，对不同剪切状态下隙宽进行渗流计算与统计分析，得到以下结论。

1）未发生剪切时，隙宽的概率密度分布满足标准高斯分布，验证了随机分形函数的可靠性；而随着剪切过程的进行，由于剪切作用破坏了裂隙面凸起面的分布，小隙宽的比例在增加，隙宽的频率分布直方图呈现单调递减的趋势，此时不在满足高斯分布的特征。

2）当Re<9.6时，Forchheimer公式与Darcy公式基本吻合，此时层流占据了主导地位；随着出口流量Q的增加，即Re>9.6时，抛物线的弯曲程度增大，裂隙水流的非线性特征越来越明显，惯性力的影响逐渐增强，此时Forchheimer公式逐渐偏离Darcy公式，裂隙中的流体开始向着紊流方向发展。

3）在剪切作用初始阶段，由于剪切作用改变了裂隙面的接触条件，接触面积增加，对水流的阻碍作用增加导致k明显减小，随着剪切的进行，接触面积继续重新分布，渗透率有所增加，但相较于剪切作用前还是有所降低。剪切位移一定时，k随入口实际流速ve增加以二次函数规律减小。

在剪切作用下，除了剪切作用本身造成的隙宽变化引起裂隙渗透性发生改变，岩石的种类以及岩石基质等因素同样会对裂隙渗流产生较大的影响，本文只单一地考虑了剪切作用，未对岩石种类等因素进行进一步的探究，在今后的研究中需要深入探究不同种类岩石的剪切作用对渗流的影响。

参考文献/References：

[1]GHAMGOSAR M，BAHAADDINI M，ERARSLAN N，et al.A new experimental approach to quantify microfractures in the fracture process zone （FPZ） under various loading conditions[J].Engineering Geology，2021，283.DOI： 10.1016/j.enggeo.2021.106024.

[2] MURALHA J，GRASSELLI G，TATONE B，et al.ISRM suggested method for laboratory determination of the shear strength of rock joints：Revisedversion[J].Rock Mechanics and Rock Engineering，2014，47（1）：291-302.

[3] BARTON N，CHOUBEY V.The shear strength of rock joints in theory and practice[J].Rock Mechanics，1977，10（1）：1-54.

[4] BAHAADDINI M，HAGAN P C，MITRA R，et al.Experimental and numerical study of asperity degradation in the direct shear test[J].Engineering Geology，2016，204：41-52.

[5] SINGH H K，BASU A.Evaluation of existing criteria in estimating shear strength of natural rock discontinuities[J].Engineering Geology，2018，232：171-181.

[6] 蔚立元，杨瀚清，王晓琳，等.循环剪切作用下三维粗糙裂隙非线性渗流特性数值模拟研究[J].岩土力学，2023，44（9）：2757-2766.YU Liyuan，YANG Hanqing，WANG Xiaolin，et al.Numerical study on nonlinear hydraulic properties of three-dimensional rough joints under cyclic shear conditions[J].Rock and Soil Mechanics，2023，44（9）：2757-2766.

[7] LI Bo，JIANG Yujing，KOYAMA T，et al.Experimental study of the hydro-mechanical behavior of rock joints using a parallel-plate model containing contact areas and artificial fractures[J].International Journal of Rock Mechanics and Mining Sciences，2008，45（3）：362-375.

[8] BAHAADDINI M.Effect of boundary condition on the shear behaviour of rock joints in the direct shear test[J].Rock Mechanics and Rock Engineering，2017，50（5）：1141-1155.

[9] SELVADURAI P A，GLASER S D.Laboratory-developed contact models controlling instability on frictional faults[J].Journal of Geophysical Research：Solid Earth，2015，120（6）：4208-4236.

[10]BARTON N.Review of a new shear-strength criterion for rock joints[J].Engineering Geology，1973，7（4）：287-332.

[11]KOYAMA T， LI Bo， JIANG Yujing， et al.Numerical modelling of fluid flow tests in a rock fracture with a special algorithm for contact areas［J］.Computers and Geotechnics， 2009， 36（1/2）： 291-303.

[12]LI Yi，CHEN Yifeng，ZHOU Chuangbing.Hydraulic properties of partially saturated rock fractures subjected to mechanical loading[J].Engineering Geology，2014，179：24-31.

[13]SUN Zihao，WANG Liangqing，ZHOU Jiaqing，et al.A new method for determining the hydraulic aperture of rough rock fractures using the support vector regression[J].Engineering Geology，2020，271.DOI： 10.1016/j.enggeo.2020.105618.

[14]SNOW D T. A Parallel Plate Model of Fractured Permeable Media[M]. Berkeley： University of California， 1965.

[15]白正雄，陳益峰，周创兵，等.压剪荷载作用下硬质岩石裂隙的峰后剪胀特性及其演化规律[J].岩石力学与工程学报，2010，29（sup2）：4131-4138.

BAI Zhengxiong，CHEN Yifeng，ZHOU Chuangbing，et al.Post-peak dilatancy and its evolution of hard rock fractures under normal and shear loads[J].Chinese Journal of Rock Mechanics and Engineering，2010，29（sup2）：4131-4138.

[16]RENSHAW C E.On the relationship between mechanical and hydraulic apertures in rough-walled fractures[J].Journal of Geophysical Research：Solid Earth，1995，100（B12）：24629-24636.

[17]ZIMMERMANR W，BODVARSSON G S.Hydraulicconductivity of rock fractures[J].Transport in Porous Media，1996，23（1）：1-30.

[18]CHEN Yifeng，ZHOU Jiaqing，HU Shaohua，et al.Evaluation of forchheimer equation coefficients for non-Darcy flow in deformable rough-walled fractures[J].Journal of Hydrology，2015，529（Part 3）：993-1006.

[19]HUANG Na，LIU Richeng，JIANG Yujing.Numerical study of the geometrical and hydraulic characteristics of 3D self-affine rough fractures during shear[J].Journal of Natural Gas Science and Engineering，2017，45：127-142.

[20]LIU Richeng，HUANG Na，JIANG Yujing，et al.A numerical study of shear-induced evolutions of geometric and hydraulic properties of self-affine rough-walled rock fractures[J].International Journal of Rock Mechanics and Mining Sciences，2020，127.DOI： 10.1016/j.ijrmms.2020.104211.

[21]DANG Wengang，WU Wei，KONIETZKY H，et al.Effect of shear-induced aperture evolution on fluid flow in rock fractures[J].Computers and Geotechnics，2019，114.DOI： 10.1016/j.compgeo.2019.103152.

[22]MA Haichun，CAO Yuan，QIAN Jiazhong，et al.Theoretical study of the mesoscopic mechanism of rock fractures during normal deformation[J].Rock Mechanics and Rock Engineering，2023，56（8）：5719-5733.

[23]ROSE H E.On the resistance coefficient-Reynolds number relationship for fluid flow through a bed of granular material[J].Proceedings of the Institution of Mechanical Engineers，1945，153（1）：154-168.

[24]BEAR J.Dynamics of Fluids in Porous Media[M].New York：American Elsevier，1972.

[25]王恩志，韩小妹，黄远智.低渗岩石非线性渗流机理讨论[J].岩土力学，2003（sup2）：120-124.WANG Enzhi，HAN Xiaomei，HUANG Yuanzhi.Discussion on the mechanism of percolation in low permeability rocks[J].Rock and Soil Mechanics，2003（sup2）：120-124.

[26]周志芳，王錦国.裂隙介质水动力学原理[M].北京：中国水利水电出版社，2004.

[27]王媛，顾智刚，倪小东，等.光滑裂隙高流速非达西渗流运动规律的试验研究[J].岩石力学与工程学报，2010，29（7）：1404-1408.WANG Yuan，GU Zhigang，NI Xiaodong，et al.Experimental study of non-Darcy water flow through a single smooth fracture[J].Chinese Journal of Rock Mechanics and Engineering，2010，29（7）：1404-1408.

[28]QIAN Jiazhong，LIANG Min，CHEN Zhou，et al.Eddy correlations for water flow in a single fracture with abruptly changing aperture[J].Hydrological Processes，2012，26（22）：3369-3377.

责任编辑：冯民

基金项目：国家自然科学基金（41831289）；国网安徽省电力有限公司项目（B6120922000S）

第一作者简介：常江（1981-），男，安徽阜南人，高级工程师，主要从事电网区域地质适宜性评价方面的研究。

通信作者：马海春，副教授。E-mail：mahaichun@hfut.edu.cn常江，姜克儒，马海春，等.岩石单结构面剪切变形渗透性演化规律［J］.河北科技大学学报，2024，45（2）：207-216.CHANG Jiang，JIANG Keru，MA Haichun，et al.Seepage evolution of shear deformation for a single rock structure surface［J］.Journal of Hebei University of Science and Technology，2024，45（2）：207-216.