基于分数阶全变分和低秩正则化的彩色图像去模糊方法

马 飞, 王梓璇, 杨飞霞, 徐光宪

(辽宁工程技术大学,a.电子与信息工程学院; b.电气与控制工程学院,辽宁 葫芦岛 125000)

0 引言

作为图像恢复中最基础的技术之一[1],图像去模糊被广泛应用于医疗影像、天文成像、智能监控等领域,获得纯净的图像十分重要[2]。图像去模糊包括图像盲去模糊和非盲去模糊两类。

图像盲去模糊的目的是根据给定的模糊图像估计出未知的模糊核和潜在的纯净图像[3]。SUN等[4]建立反卷积模型最终估计出模糊核的宽度和方向;DONG等[5]将L0范数与全变分正则项组合起来提出了一种新的自然图像先验; BAI等[6]提出了一个基于图像的盲去模糊算法,但其高度不适定性会导致模糊核的不确定,使去模糊效果大打折扣。

图像非盲去模糊是指在已知模糊核的前提下,恢复出潜在图像的过程。经典的非盲去模糊方法主要分为深度学习方法[7-8]、滤波法[9-10]、正则化法[11-16]3类。ZHANG等[7]训练一个迭代非盲的全卷积网络用于去除梯度域内的噪声,但大量的训练数据集会降低小样本图像恢复准确率;CRUZ等[9]提出的滤波方法,减少了边缘模糊效应,但是对加性噪声特别敏感,恢复效果不佳。比较经典的正则化方法如全变分(TV)正则项[15,17],但TV正则项考虑的是像素点处的一阶差分,会产生阶梯效应。一些研究者在传统TV正则项上进行了改进。CHOWDHURY等[18]提出了分数阶全变分(FTV);GUO等[19]证实FTV可以更准确、更精细地表示图像纹理,缓解阶梯效应。由近年来的相关工作发现,对图像施加低秩先验约束[20-21],能够保留边缘信息并消除潜在图像中不重要的纹理,同时还能抑制噪声对去模糊过程的影响。然而,现有的正则化方法没有考虑到彩色图像RGB 3个通道具有高度相关性,会引起图像处理前后颜色突变的问题[22]。

为了克服上述问题,本文提出了一种基于分数阶全变分和低秩正则化(LRFTV)的彩色图像去模糊方法。首先,分析并证明了RGB转换为YCbCr后的去模糊方法是合理的,保持了色彩平衡;其次,通过自然图像局部平滑性质和低秩性质提出了分数阶全变分和低秩正则化的保真度项,既缓解了图像去模糊中出现的阶梯效应和伪影,又增加了图像细节;最后,利用交替方向乘子 (ADMM) 法进行优化求解,恢复出纯净图像。

1 信号模型

在高斯噪声条件下,对应的图像去模糊退化模型可以写为

B=A⊗X+E

(1)

式中:B、X、E分别为模糊图像、潜在图像和噪声;A为某种类型的模糊核;⊗表示卷积运算。

1.1 分数阶定义

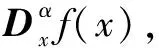
(2)

式中,权重gα(l)为

(3)

式中,Γ(·)为伽马函数,对于指定的微分阶α可取任意正实数。

将一幅图像推广到二维离散化,可以表示为欧几里德空间Rm×n中的一个矩阵,即图像X。其分数阶的微分形式为

(4)

当式(3)中的l趋于0时,gα(l)的幅度很快衰减到零,因此只选择合适的分数阶推导的项作为近似。得到图像X∈Rm×n沿垂直和水平方向的离散分数阶差分并取前L项近似的截断版本为

(5)

(6)

然后将FTV定义为

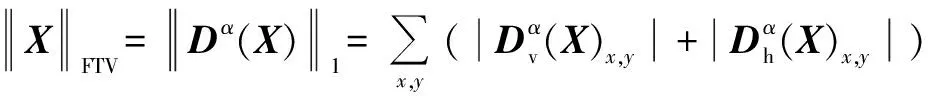
(7)

1.2 低秩正则项

秩的最小化是一个求解困难的非凸问题,可以采用凸松弛技术处理。核范数正则化作为秩约束问题的一种凸松弛表示,核范数最小化(NNM)方法证明了核范数是秩最小化问题的最紧凸松弛,并且得到了该问题的解

(8)

X*=USη(Σ)VT

(9)

其中,参数η>0,B∈Rm×n,假设m≥n,B=UΣVT,为矩阵B的奇异值分解,可以通过软阈值算子收缩奇异值,将软阈值算子定义为

(10)

式中:τ表示变量;T表示阈值。然而,奇异值的重要程度是不同的,较大的奇异值表示主特征分量包含了更丰富的信息,较小的奇异值包含细节特征及噪声。为了提升核范数正则化的有效性,对不同的奇异值赋予不同的权值,因此,提出了加权核范数正则化(WNNM)方法,将矩阵X的加权核范数定义为

(11)

式中:Xj表示X中所有相似的图块堆叠成的一个矩阵;σi(Xj)为第i个奇异值,σ1(Xj)≥σ2(Xj)≥…≥σn(Xj)≥0;*表示核范数;权重向量w=[ω1,…,ωn],ωi≥0,其权重设置为

(12)

式中:c为矩阵的列数,即所选的相似图块数量;ε为无限小的数。此权值满足0≤ω1≤ω2≤…≤ωn,使较大的奇异值收缩更小,较小的奇异值收缩更大,以保留数据矩阵中主要的信息。

2 提出的算法

本文旨在建立图像去模糊的正则化模型以及设计相应的算法,在式(1)中提出了一个去模糊模型,并且考虑以下正则化问题

(13)

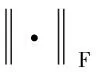
(14)

构造增广拉格朗日函数

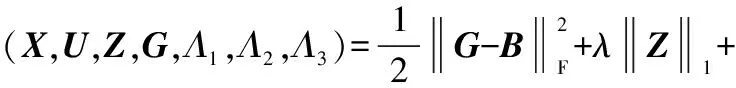
(15)

式中:Λi为对偶变量;μi为增广拉格朗日的权重系数。

2.1 X的解析表达式

从增广拉格朗日函数中提取X的项,可得

(16)

初始的σi(Xj)可以估计为

(17)

然后,通过广义软阈值算子soft(τ,T)收缩奇异值,迭代得到最优的Xk+1的解。

2.2 U的解析表达式

通过求解U的梯度,得到了一个闭式解

(18)

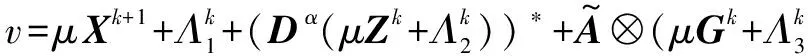
(19)

2.3 Z的解析表达式

通过调用已知的软阈值算子soft(τ,T),且当τ>0,可得Z的更新为

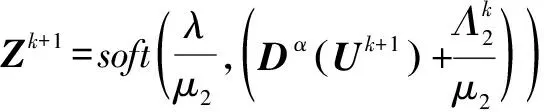
(20)

2.4 G的解析表达式

(21)

解得G为

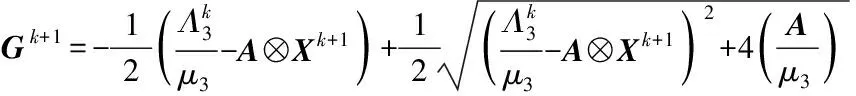
(22)

3 仿真实验结果及分析

为了验证本文提出的基于分数阶全变分和低秩正则化(LRFTV)的彩色图像去模糊方法的图像去模糊效果,在CSet8图像集上进行了实验,大小为256×256×3,单位为像素。实验中,采用高斯模糊核和运动模糊核两种类型的模糊核产生模糊图像,利用IAWCTT[23]、FCNN[7]、L0-RIG[5]和GBID[6]4种去模糊方法作对比算法,图像恢复性能的评价核心指标为峰值信噪比(PSNR)和结构相似度(SSIM)。

一是爱在“困难”处。通过入户走访了解群众困难诉求，分析研究对策解决。帮助170人实现就业，解决117人看病难、75名学生上学难、11户贫困户住房难问题；二是爱在“细微”处。通过换灯泡、修马桶、探望住院群众等一个个微行动，增进了和职工群众的感情赢得群众信任。截至目前，为群众扶贫帮困298户次，为民办实事近300件；三是爱在“急需”时。共开展互助帮扶活动110余次，逢年过节走访慰问，给特殊困难家庭发放慰问款物6.24万元。

3.1 亮度通道去模糊的有效性分析

本文提出了在YCbCr颜色空间的亮度通道中实现去模糊处理。从模糊的图像数据集、GoPro数据集、CSet8数据集中共计选取20幅图像,图1所示为不同颜色空间中各通道的MSE曲线。

图1 20幅纯净图像及其模糊图像在不同通道中均方误差Fig.1 The MSE of 20 clear images and blurred images in different channels

图1(a)中,3个通道的MSE曲线在RGB颜色空间中均发生了显著变化,因此模糊会对RGB的3个通道都造成影响。图1(b)中,仅有Y通道的MSE有明显变化,可以得出,在RGB颜色空间中模糊影响了3个通道,从而出现色彩失衡现象,而在YCbCr颜色空间中模糊主要施加在了亮度通道上,因此,在亮度通道中实现的去模糊方法是合理的。

3.2 参数设置

以 Lena图像为例,反映了α=0.2的高斯模糊和α=0.3的运动模糊的参数及权重系数的变化曲线,如图2所示。

图2 不同参数去模糊的PSNR

从图2结果可知,设置λ=1、β=1.6、μ1=0.1、μ2=0.1、μ3=0.1,性能达到最优,这些权重系数是用来平衡数据拟合项与正则项之间的关系的。设置模糊图像相似斑块大小为88,单位为像素,相邻图像分块之间重叠1个像素。对于每个分块,使用块匹配算法[20]在30×30(单位为像素)的邻近范围内确定相似的分块。

3.3 仿真与性能分析

3.3.1 不同分数阶阶次的图像去模糊性能

本文提出的LRFTV方法中α的选择影响着图像的质量,图3所示为不同α下PSNR曲线。

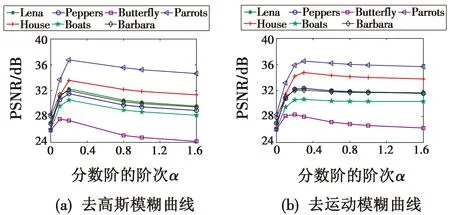
图3 不同α下的PSNR

由图3(a)可知,当去高斯模糊的α取0.2时,PSNR达到最佳;由图3(b)可知,当α取0.3时,去运动模糊的PSNR达到最佳。分数阶微分对不同种模糊有不同的影响,因此,选择适合不同模糊图像特征的阶次建立去模糊方法进行实验仿真。

选择不同模糊核尺寸,即改变图像的模糊程度会对图像恢复效果产生不同的影响,通过对Lena图像进行标准差不同的高斯模糊处理,如图4所示。

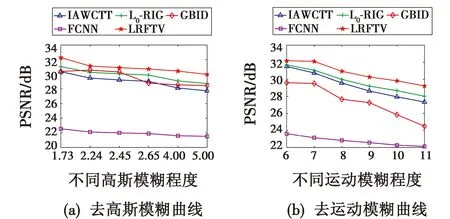
图4 不同模糊程度的PSNR

由图4(a)可知,本文方法的PSNR性能最优;通过图4(b)横向比较发现,当模糊程度增大时,PSNR也随之变小。这主要是因为模糊核尺寸的增加导致图像差异度边缘的模糊程度更高,图像恢复难度提升,所以图像恢复性能下降。

3.3.3 不同噪声的图像去模糊性能

采用6种均值为0且方差不等的高斯噪声加入Parrots模糊图像,如图5所示。

图5 不同噪声下图像去模糊的PSNR

从图5可以看出,在不同模糊特征下,各方法的PSNR均随着噪声的增大而减小,这是因为噪声增加导致有效图像信号的提取难度提升;对比方差为0.1和0.6的各方法,LRFTV方法对图像的PSNR值差异不明显,且均高于其他方法,这是因为分数阶全变分和低秩正则项能有效抑制噪声的干扰。

3.3.4 不同正则项的图像去模糊性能

表1给出了不同正则项去模糊的性能,分别对Peppers去高斯模糊处理以及Butterfly去运动模糊处理。本文表中加粗数据表示效果最优。

表1 不同正则项去模糊的PSNR Table 1 PSNR of deblurring with different regularization dB

由表1可知,本文提出的LRFTV方法均获得了最优的PSNR,全变分和低秩组合的性能次之。因此,本文方法有很大的优势。

3.3.5 不同方法的图像去模糊性能

表2 不同测试图像去高斯模糊问题中的PSNR和SSIM Table 2 PSNR and SSIM in Gaussian deblurring of different test images

表2中,FCNN利用了CNN网络的方法,本文方法取得了相对最好的效果,测试图像集的PSNR均在27.38 dB以上,SSIM均在0.95以上,其中,Parrots取得了最高的PSNR值36.76 dB。本文方法在7幅测试图像上的平均PSNR比L0-RIG高出1.74 dB。

图6为各种方法在测试图像Peppers上的去高斯模糊的效果。

图6 去高斯模糊的效果对比Fig.6 Effects of Gaussian deblurring

由图6可知:IAWCTT方法能够大体实现图像的去模糊,但是细节恢复不好;L0-RIG方法较前面方法性能有所提升,但是仍然有很多细节并未恢复出来,且在图像边缘处产生了伪影,使图像边缘处信息丢失;GBID方法虽表现出不错的去模糊性能,但是此方法会产生阶梯效应,在去除纹理边缘方面较弱;FCNN方法在细节部分恢复效果很好,但在边缘处会产生伪影;而本文所提LRFTV方法对于细节的恢复更加精细,也在很大程度上缓解了阶梯效应的存在,同时也抑制了伪影的产生。

表3给出了模糊角度35°,模糊长度为6像素的各方法去运动模糊性能。

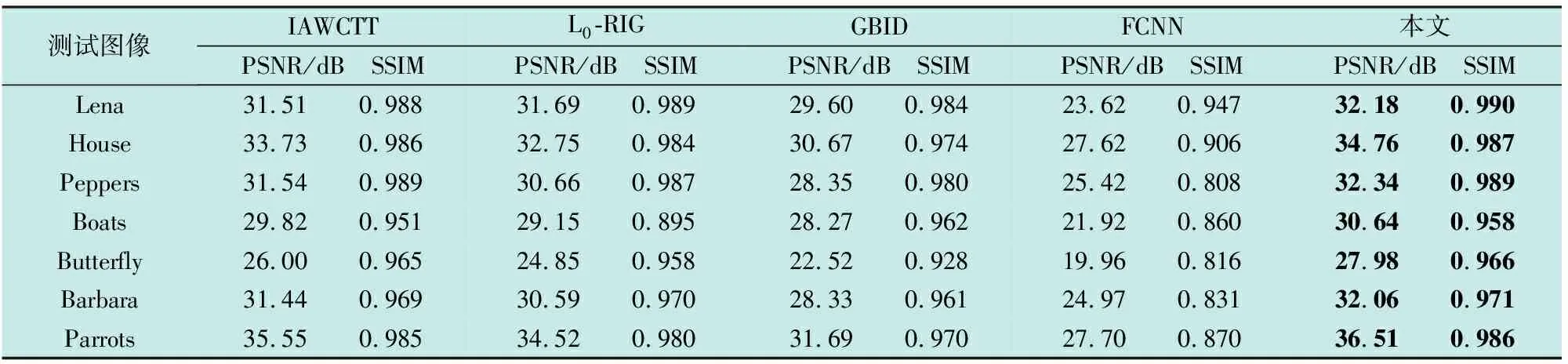
表3 不同测试图像去运动模糊问题中的PSNR和SSIM Table 3 PSNR and SSIM in motion deblurring of different test images

由表3可知,同去高斯模糊相似,在测试图像上本文方法的平均PSNR和SSIM均高于其他方法,其中,FCNN方法取得了相对最低的PSNR,Parrots取得了最高的PSNR值36.51 dB。本文方法在7幅测试图像上的平均PSNR比L0-RIG高出1.75 dB。

图7为各种方法在测试图像Parrots上去除运动模糊后的效果图。

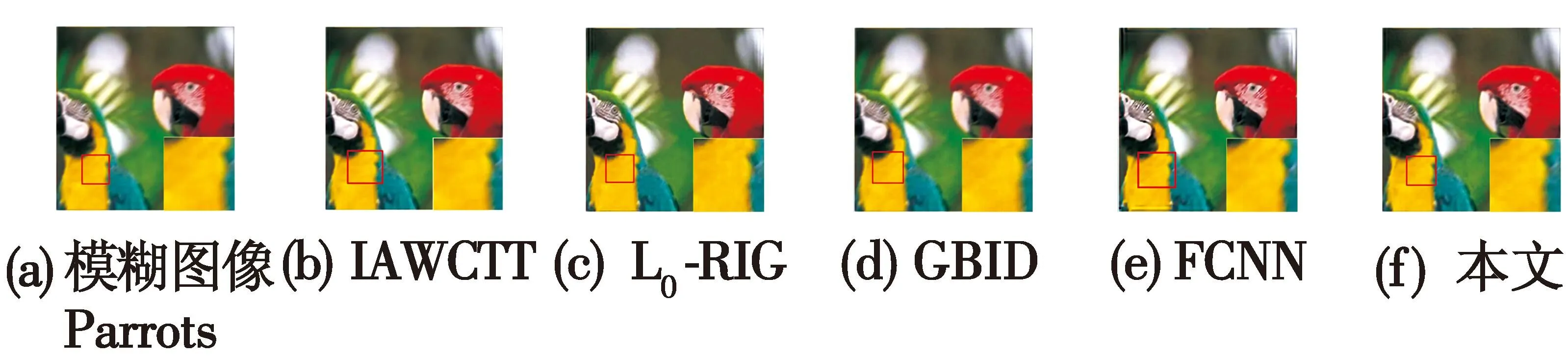
图7 去运动模糊的效果对比Fig.7 Effects of motion deblurring

由图7可知,对比视觉效果,本文方法恢复出的纯净图像效果较好,在一定程度上缓解了阶梯效应,且能更好地重建细节边缘信息,去除伪影,具有比较高的稳定性。

3.3.6 不同方法的图像去模糊运行时间

表4为不同方法的平均运行时间。

表4 不同方法的平均运行时间

由表4可知,FCNN恢复图像最耗时,本文方法和GBID方法耗时很接近,两者运算时间相差非常小,这可能是因为两种方法都需要正则优化求解,而FCNN需要不断迭代获取稳定的网络参数,因此消耗了大量时间。

4 结束语

本文提出了一种基于分数阶全变分和低秩正则化的彩色图像去模糊方法。证明了YCbCr的Y通道与CbCr两个色度通道之间是不互相干扰的,保持了色彩平衡,通过引入分数阶全变分和低秩正则化来表征图像的两个不同特征,可以更好地约束解空间,增强图像的细节并减少阶梯效应和伪影。实验结果表明,本文方法不仅在客观评价指标方面取得了很好的效果,使PSNR最少提升了1.74 dB,而且在主观视觉方面恢复出了质量更好的图像。在未来的研究中,将进一步改进方法,缩短运行时间,同时为了更全面地分析该方法的有效性,将拓展该方法用于去雨、去雾等其他图像复原任务。