自适应蚁群算法的无人机三维航迹规划

张 骜, 毛海亮, 卞 鹏, 陈 侠

(1.沈阳科技学院,沈阳 110000; 2.海鹰航空通用装备有限责任公司,北京 100000)

0 引言

无人机(UAV)是一种由自带的程序控制器或无线电远程控制的无人驾驶飞行器。近年来,随着自动化领域的飞速发展,为了最大限度地减少人为干预,降低危及生命的风险,无人机系统在军事、工业、农业等诸多领域受到广泛关注,其应用范围日趋广泛。航迹规划技术作为无人机系统中必不可少的关键技术[1-3],是执行任务的重要手段。

航迹规划是考虑无人机在能够顺利完成既定任务的同时,规划出从起点到目标点的躲避障碍的飞行路径。目前,航迹规划的研究越来越受重视。航迹规划算法主要包括传统航迹规划算法和智能航迹规划。在传统航迹规划算法中,人工势场(APF)法[4]、A*算法[5]、Dijkstra算法[6]尤为重要。智能优化算法的典型代表包括粒子群算法(PSO)[7]、遗传算法(GA)[8]、蚁群算法(ACO)[9]等,其中,蚁群算法是根据大自然中蚂蚁觅食过程而提出的算法。蚁群算法不断更新当前路径,直至找到一条最优路径,由于该算法具有鲁棒性强、信息反馈好等优点而受到广泛关注,但其存在着收敛速度慢、效率低、容易陷入局部最优值等问题,于是,诸多学者对该算法不断进行改进,优化其性能。

文献[10]提出基于球面矢量的粒子群优化算法,将航迹规划问题转换为优化问题,根据代价函数找到路径代价最小的航迹;文献[11]采用平滑器优化粒子群算法性能的参数,消除不规则误差,并且采用大都会准则作为接收策略模型,解决了局部最优解的问题;文献[12]针对原始蚁群算法会发生收敛慢的问题,引入角度导向因子和启发式信息自适应调整因子,并融合了航迹优化的目标函数,该优化算法缩短了收敛时间;文献[13]提出新的状态转移函数,并且改进了信息素的更新规则,提高了信息素质量,加快了信息素积累速度,引入信息调节因子以解决局部最优的问题;文献[14]建立航迹规划数学模型,并且融入自适应并行策略,不仅实现全局搜索而且还实现了局部搜索,该算法加快了收敛速度;文献[15]改进了启发式函数和信息素更新方法,采用非均匀初始信息素方法,防止蚂蚁走无效的路径,该算法缩短了收敛到最优解的时间;文献[16]提出改进信息素挥发系数,并且引入飞行条件约束,提高了航迹规划算法的实时性,并且通过几何方法更新质量较低的节点,证明了该算法的优越性;文献[17]建立了威胁模型,并在蚁群算法中融入Q-学习算法解决容易出现局部最优值的问题,传统的蚁群算法生成航迹后,采用二次B样条曲线优化航迹,从而获得平滑飞行路径;文献[18]融合改进人工势场方法和蚁群算法,加入潜在力和快速函数的融合蚁群算法,解决了局部最优的问题,缩短了收敛到最优解的时间等。虽然对蚁群算法的改进已经取得了初步研究成果,但大多文献关注的是基于蚁群算法的二维航迹规划算法研究,而对于三维空间,改进蚁群算法的航迹规划的研究成果较少。因此,对改进蚁群航迹规划算法的研究仍具有一定的提升空间,需要进一步优化改进蚁群算法的性能指标。

受上述文献的启发,提出了自适应蚁群算法的无人机三维航迹规划算法,在三维空间中,采用网格式划分空间,提出新的蚁群算法启发式信息、状态转移概率和信息素更新规则,提高了新算法的全局规划能力,提升了搜索效率。然后,建立基于路径长度和转弯角度的目标函数,使无人机获得三维的全局较优路径,与原算法相比,提出的算法规划航迹收敛时间更短,路径更加平滑。

1 三维环境建模

图1所示为三维搜索空间模型。

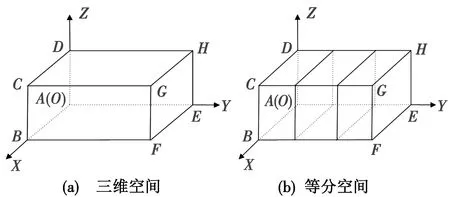
图1 三维搜索空间模型示意图Fig.1 Schematic diagram of 3D search space model

图1中,创建O-XYZ三维坐标,并在当前的三维坐标系中构建三维区域ABCD-EFGH。当建立三维空间时,用等分空间法划分整个三维空间[19]。首先,空间ABCD-EFGH沿AE侧(即沿Y轴)分成m个等部分,将产生m+1个平面;然后,任何平面可以沿AB侧分为(即沿X轴)n等分,沿AD侧(即沿Z轴)分为l等分,因此整个三维空间将被划分为n×m×l个立方体。每一个立方体对应一个空间节点。

在空战环境中,敌人往往会部署一些静止的威胁(如雷达、干扰设备和防空武器等),从而影响到无人机的正常飞行。为了防止无人机在飞行过程中误入敌人的攻击范围,保障无人机的安全,必须建立一个敌人的威胁模型[20]。图2给出了静态威胁模型不同视角下的3D模型,图中,球体表示静态威胁。

图2 静态威胁模型示意图Fig.2 Diagram of a static threat model

2 三维航迹规划算法

2.1 改进的三维信息素函数

在基本的蚁群算法中,初始信息素的浓度分布是均匀的。在初期,蚂蚁采用启发式信息来选择可行节点,而启发式信息往往与可行节点和目标点之间的距离有关,这很可能导致规划出的航迹陷入局部最优的情况。并且,由于起点往往距离终点很远,起点附近的节点启发式信息相近,这将导致算法在早期盲目搜索,消耗大量时间。所以在算法的初始阶段,引入非均匀的初始化信息素,从而有效地提高了蚁群算法的搜索速度。图3为信息素示意图。

图3 信息素示意图Fig.3 Pheromone diagram

如图3所示,在不考虑障碍的前提下,将无人机的起点S和终点G(即目标点)连为一条直线,每个空间节点的信息素与该点到直线SG的距离有关。

蚂蚁在觅食过程中优先选择直线SG附近的空间节点时,到达目标点所用的距离会比选择其他节点时更短。表现在信息素的分布上,即距离直线SG越近的空间节点,所含的信息素浓度应该越高,使蚂蚁有更大的概率选择距离直线SG更近的空间节点。在数学坐标系中,常见的第一象限衰减函数有y=x-0.5,y=1/x,y=e-x。将x比作空间节点距直线SG的距离,y为该空间节点的信息素,3种衰减函数如图4所示。通过比较3种衰减函数发现,若使用y=1/x,y=e-x这2种函数对初始信息素进行定义,当x趋近于50时,y趋近于0,这表示当空间节点距离直线SG稍远时,该点的信息素将趋近于0,这将不利于提升算法的全局搜索能力,尤其当起点与目标点间障碍物较多时,会增加无人机碰撞的风险。因此,选用y=x-0.5作为信息素的衰减函数。

图4 3种衰减函数Fig.4 Three kinds of attenuation function

三维环境中的改进信息素浓度表达式为

(1)

式中:d为欧氏距离;dQ(xi,yj,zk)为空间节点到直线SG的欧氏距离。

2.2 改进的三维启发式函数

在无人机实际飞行过程中,危险不仅来源于障碍等威胁,无人机的飞行高度过高或者过低也会导致无人机发生危险。为了保证无人机飞行期间的安全,引入了安全启发因子S,表示为

(2)

式中:h为下一可行节点的高度;hmax为无人机安全飞行的高度上限;hmin为无人机安全飞行的高度下限。

改进后的三维启发式信息可以表示为

(3)

ε=exp(-2(Nc/Nmax)2)

(4)

式中:djG为下一可行节点j到目标点G的距离;ε为自适应调整因子;Nc为当前迭代次数;Nmax为最大迭代次数。在算法的早期,由于ε接近于1,可以加强启发式信息的作用,加速算法的收敛;在算法的后期,由于ε远小于1,会削弱启发式信息的作用,从而提高算法的全局搜索能力。

2.3 改进的三维状态转移规则

蚂蚁在三维空间中的状态转移概率可以表示为

(5)

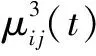
(6)

χ=(Nmax-Nc)/Nmax

(7)

其中:a为常数;χ为调整因子;θ为点i(xi,yi,zi)至点j(xj,yj,zj)的连线与点i(xi,yi,zi)至目标点G(xG,yG,zG)的连线所成夹角,取值范围为[0°, 180°]。

图5为三维角度示意图,其中,i为当前节点,j为下一步可行的节点。

图5 三维角度示意图Fig.5 Three-dimensional angle diagram

参数自适应伪随机比例规则表达式为

(8)

(9)

其中:q为[0, 1]之间的随机数;q0为自适应转换概率的阈值;δ0为比例系数。

图6为三维飞行示意图。

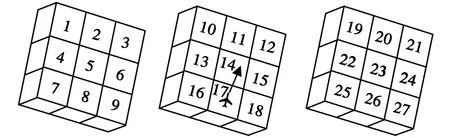
图6 三维飞行示意图Fig.6 Three-dimensional flight diagram

如图6所示,当无人机从17号栅格飞往14号栅格时,下一步的可行节点有{1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 15, 16, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27},根据不同无人机的偏转角度约束条件,可以将与无人机飞行方向相悖的节点{7, 8, 9, 16, 18, 25, 26, 27}从待扩展节点中删除,减少待扩展节点,提高搜索效率;也可根据需要进一步将节点{4, 5, 6, 13, 15, 22, 23, 24}从待扩展节点中删除,可行节点进一步缩减为{1, 2, 3, 10, 11, 12, 19, 20, 21}。

2.4 改进的三维信息素更新规则

建立的信息素浓度更新为

(10)

(11)

其中:pbest是当前迭代的最优路径;ρ为自适应信息素挥发因子;T和Jk分别是常数和蚂蚁k当前迭代路径的性能指标。

中外教师合作教学是指在大学英语教学中，设置专门的文化教学课堂，根据文化目标和教材文化方面的内容，中外教师共同研讨、制定文化教学的主题，然后由外教进行目的语文化的输入，在课堂上采取以外教为主、中方教师(大学英语教师)为辅，中外教师共同组织课堂的教学模式。

信息素的更新规则

(12)

(13)

其中:Jbest为当前迭代最优路径性能指标值;Jworst为当前迭代最差路径的性能指标值;Qbest为当前迭代的最优路径;Qworst为当前迭代的最差路径;ρt为自适应信息素挥发因子。

在蚁群算法寻找最优解的过程中,除了信息素浓度的更新规律外,信息素挥发因子也处于重要地位。为了加快收敛速度,提高全局规划能力,定义了自适应信息素挥发因子ρt为

(14)

式中:调整系数κ为小于1的正数;LSG为从起始网格S到路径的目标网格G的欧氏距离;Lk为蚂蚁k当前迭代路径的路径长度。在算法的早期阶段,由于路径长度Lk较大,挥发因子ρt也较小,每条路径上的信息素浓度差值小,增大了蚂蚁的全局搜索范围,增加了路径的多样性。随着路径长度Lk越来越小,挥发因子ρt迅速变大,不同航迹上的信息素浓度差变大,从而增强了蚁群的导航功能,加快搜索速度,进而使算法收敛速度更快。

2.5 三维航迹规划目标函数

1) 长度指标函数。

三维环境下的长度指标函数L(Q)可以表示为

(15)

(16)

其中:n为无人机经过的路径点总数;Qi为路径上的第i个点,(xi,yi,zi)为Qi的坐标,d(Qi,Qi+1)为从Qi到Qi+1的欧氏距离。

2) 角度指标函数。

三维环境下的角度指标函数E(Q)可以表示为

(17)

式中:δ(li,li+1)为三维空间中无人机从当前航线进入下一点的偏航角度;ε(li,li+1)为俯仰角度;ky为偏航角的权重参数;kp为俯仰角的权重参数。无人机由Qi-1点飞至Qi点后,再由Qi点飞至Qi+1点,计算一次δ(li,li+1),ε(li,li+1)。

图7为三维转角示意图。

图7 三维转角示意图Fig.7 Three-dimensional turning angle diagram

如图7所示,将3个空间节点投影在同一平面内计算δ(li,li+1),ε(li,li+1)同理。

三维无人机航迹优化的目标函数J(Q)定义为

J(Q)=kL·L(Q)+kE·E(Q)

(18)

式中,kL和kE分别为长度指标和角度指标的权重,且满足kL+kE=1。在算法完成所有迭代后,得到使目标函数J(Q)达到最大值maxJ(Q)的路径,并将其视为最优路径。

3 仿真分析

将本文算法和其他两种算法进行仿真比较,其中,算法1是传统蚁群算法,算法2是文献[19]的二维算法应用于三维无人机航迹规划的改进蚁群算法。算法的重要参数如表1所示。

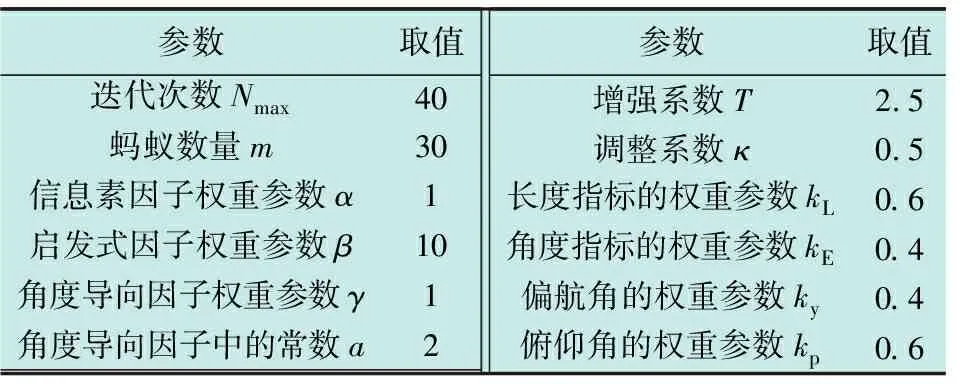
表1 重要参数及取值

3.1 环境1

环境1地图设置为20 km×20 km×20 km,无人机飞行起点坐标为(1 km,1 km,1 km),目标点坐标为(20 km,20 km,20 km),环境1中障碍分布信息如表2所示。

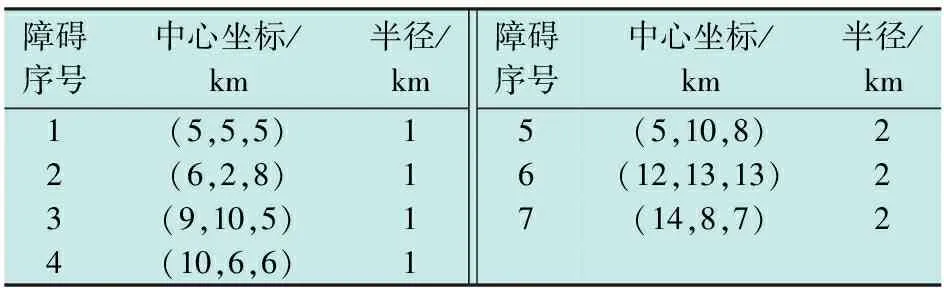
表2 环境1障碍信息

将3种算法分别在环境1中运行40次,并记录3种算法的性能指标,如表3所示。

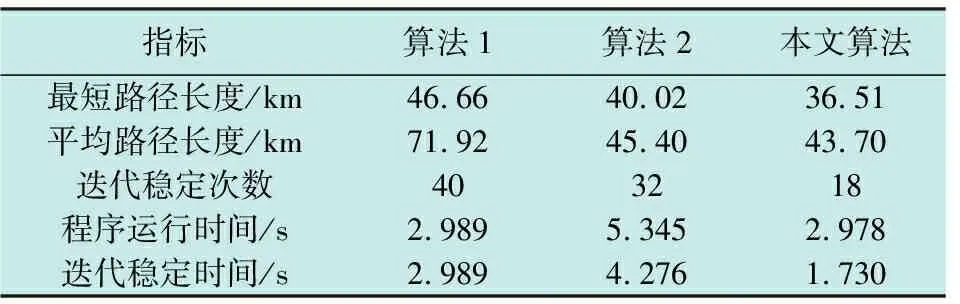
表3 环境1实验数据

各算法产生的无人机飞行航迹如图8所示,每种算法的收敛曲线如图9所示。

图8 环境1飞行航迹Fig.8 Flight path diagram for Environment 1

图9 环境1的收敛曲线Fig.9 Convergence diagram for Environment 1

由表3、图8、图9可以看出,算法2规划的最短路径长度相较于算法1规划出的最短路径长度缩短了约14.2%,40次迭代的平均路径长度缩短了约36.9%,但算法2的运行时间明显长于算法1,并且收敛速度并不理想。而本文算法运行时间更短、航迹抖动较少、更加平滑,最短路径长度相较于算法1规划出的最短路径长度缩短了约21.8%,相较于算法2缩短了约8.8%;40次迭代的平均路径长度相较于算法1缩短了约39.2%,相较于算法2缩短了约3.7%。可以看出,在保证快速收敛的前提下,与其他算法相比,本文算法可以获得更优的路径,各项性能指标均最优。

3.2 环境2

环境2地图设置为30 km×30 km×30 km,无人机的飞行起点和终点坐标分别是(1 km,1 km,1 km)和(30 km,30 km,30 km),在环境2中的障碍分布信息如表4所示。

表4 环境2障碍信息

将每种算法分别运行40次,并记录下算法的性能指标,如表5所示。无人机飞行航迹与各算法迭代曲线分别如图10与图11所示。

表5 环境2实验数据

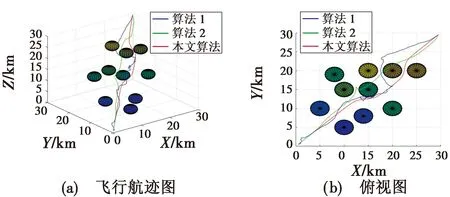
图10 环境2飞行航迹Fig.10 Flight path diagram for Environment 2

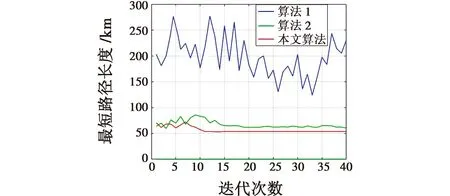
图11 环境2的收敛曲线Fig.11 Convergence diagram for Environment 2

由表5可以看出,本文算法相较于算法1规划出的最短路径长度缩短了约57.22%,平均路径长度缩短了约71.37%,相较于算法2规划出的最短路径长度缩短了约10.83%,平均路径长度缩短了约15.30%。本文算法不仅加快了收敛速度,同时也缩短了运行时间。

由图10和图11可以看出,在蚂蚁数量和迭代次数相同的情况下,算法1已经不能适用于复杂的环境,不仅容易陷入局部最优,收敛速度较慢,规划的路径也较长、较曲折。

4 结束语

本文提出一种改进型自适应蚁群算法的无人机三维航迹规划算法。根据起点和目标点建立了一种不均匀的初始信息素矩阵,同时在启发式信息中引入安全启发因子和自适应的信息素挥发因子,提高了算法前期的全局搜索效率,并在算法的后期缩短了收敛到最优解的时间,同时将偏航角和俯仰角加入到目标函数中,建立了航迹优化目标函数。实验结果表明,与蚁群算法和改进蚁群算法[19]相比,提出的三维航迹规划算法更适用于三维空间,并且运行时间更短、收敛速度更快,规划出的航迹也更短、更平滑。但本文算法只考虑了静态威胁,在实际环境中往往有许多事先未探测到的障碍,或是移动障碍,因此,下一步将把动态环境下的无人机航迹规划问题作为研究重点。