集群无人机协同导航构型优选方法

马铭江, 熊 智,2, 王 融,2, 陈明星

(1.南京航空航天大学自动化学院导航研究中心,南京 211000; 2.先进飞行器导航、控制与健康管理工业和信息化部重点实验室信息化部重点实验室,南京 211000; 3.安徽工程大学电气工程学院,安徽 芜湖 241000)

0 引言

近年来,由多架无人机构成的无人机集群受到更多的关注,可被用于无人侦察、空中与地面监视等作战场景,在执行危险和复杂任务的能力方面具有突出的优势[1]。因此,开展集群无人机协同导航方法研究,充分发挥集群无人机的协同效能,成为了目前国内外在该领域的主流研究方向[2-3]。

准确的导航信息是集群无人机实现自主协调的关键。在多数环境下,集群无人机中的所有无人机均可依赖于全球卫星导航系统(GNSS)来获得导航定位信息。然而,当集群无人机中的部分无人机因自身器件故障或外部环境干扰而无法接收卫星信号时,该无人机的导航定位精度将会受到影响。此外,在卫星拒止环境中,集群无人机之间的信息交互则是队形维持和避免碰撞的前提[4],各无人机之间可以通过协同测距信息的测量进行信息交互,提升集群无人机导航系统的可靠性和稳定性。

集群无人机机间距离测量和信息传输可采用超宽带(UWB)及数据链通信技术实现。文献[5]提出了北斗卫星导航系统/数据链紧组合方案,在观测条件不足的情况下提升组合导航系统的定位精度;文献[6]研究了超宽带点对点无线电测距的无人机相对导航方法;文献[7]建立了GNSS拒止下无人机与无人车的协同导航系统,利用无人车之间点对点无线电测距改善了无人机的定位精度。无人机的空间构型是集群无人机在同一时空下的位置分布,良好的空间构型是集群无人机协同导航的基础,通过开展构型优选研究,分析不同构型对定位精度的影响并采用最优构型优选方法可进一步提升集群无人机的整体精度。

当前导航构型优选的准则和依据主要是几何精度因子(Geometric Dilution of Precision,GDOP)[8]。通过对GDOP的计算选择最优空间中的多架锚机对用户机进行协同定位解算,从而提升了无卫星信号下用户机的定位精度。文献[9]提出一种结合无人机测距误差、时钟误差和位置误差的协同精度因子(Cooperative Dilution of Precision,CDOP)计算方法,为路径规划和大量机间信息筛选提供了一种新的思路。与传统方法相比,CDOP可以更精确地描述锚机的定位性能,对构型优选的研究具有重要意义。然而,采用GDOP或CDOP进行分析时,算法每次优化都要遍历求解所有构型的GDOP或CDOP值,难以满足运算实时性需求。针对上述问题,文献[10]提出采用遗传算法(GA)实现选星,通过GA的快速搜寻能力从而减少GDOP的计算次数。此外,粒子群优化 (PSO) 算法作为一种随机寻优算法,常用于处理非线性复杂系统的优化问题,可用于集群编队这类实时性要求较高的应用场景,进一步减小集群协同导航的运算量,提升系统实时性[11]。但PSO算法存在寻优过程中容易陷入局部最优导致寻优结果不准确的问题[12],因此,可采用改进的粒子群优化算法,提高算法寻优能力以及全局收敛能力[13]。

基于上述分析,本文提出了一种集群无人机协同导航构型优选方法,用于提升无人机群的定位精度和计算效率。首先采用机间相对测距的方式获得无人机间的相对距离,并在现有GDOP方法基础上,创新性地采用CDOP分析方法,以CDOP值为适应度函数改进构型优选标准。在此基础上,利用自适应惯性权重和非对称学习因子对现有PSO算法进行改进。最终,在保证计算效率的同时,筛选出最优几何构型,实现了大量协同信息下的信息优选,提升了算法的寻优性能和收敛速度。

1 协同导航构型优选方案

1.1 协同导航构型优选方案设计

集群无人机在协同执行作战任务时,部分无人机因自身器件故障或外部环境干扰而无法接收卫星信号时,集群中其余无人机可以对其进行协同辅助定位。具体场景如图1所示。

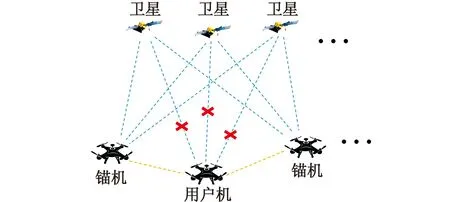
图1 协同导航构型优选示意图Fig.1 Schematic diagram of configuration optimization for collaborative navigation

集群中的所有无人机均配备GNSS和惯性导航系统(INS),同时,搭载UWB测距设备以获得无人机之间的相对距离。其中,处于卫星不可用下的无人机称为用户机,其余无人机称为锚机。在众多锚机向用户机发出冗余协同信息的情况下,用户机如何快速且准确地选取最优的协同信息进行定位是本文的研究重点。

1.2 协同导航构型评估

集群无人机群中,用户机可接收到所有锚机的导航信息,并在冗余信息中提取最优协同信息进行定位解算。因此,需要对最优构型下用户机的定位精度展开评估。

在卫星导航定位系统中,用卫星构架的几何性质表征卫星定位精度的物理量叫作精度因子(Dilution of Precision,DOP)。类比于卫星,集群无人机中的定位精度也会受到集群无人机空间构型的影响。此外,集群无人机中的每一架无人机都要考虑自身的定位精度。因此,采用协同精度因子(CDOP)展开研究,更加符合集群无人机协同导航的场景。CDOP是用集群无人机构型的几何性质以及集群无人机自身定位误差来表征集群中无人机的定位精度的物理量。对于集群无人机协同导航系统而言,用户机的位置为Xi=[xi,yi,zi]T,锚机的位置为Xj=[xj,yj,zj]T,j∈Uj,Uj,代表用户机测距范围内的其他锚机的集合。用户机与集群中锚机的距离dij可以定义为

(1)

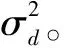
(2)

(3)

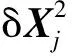
同理,通过n架锚机对用户机进行定位,可得

(4)

由于不同距离的测距误差相互独立且同分布,则测距误差的协方差为

(5)

式中,I代表单位矩阵。结合式(4),(5)可得

(6)

式中,G代表系数矩阵。对于用户机,其CDOP可以定义为

(7)

1.3 协同导航最优构型筛选方法

本文采用PSO算法来减少CDOP的计算次数,从而提高集群无人机协同定位的实时性。在N维空间中,有n个粒子,则粒子i的位置表示为xp=[xi1,xi2,…,xiN],粒子的飞行速度表示为Vi=[vi1,vi2,…,viN],i=1,2,…,n。搜索到的粒子的历史最优位置称为个体最佳位置pbest=[pi1,pi2,…,piN],除此之外,各粒子所知目前为止整个群体中的所有粒子发现的最好的位置称为全局最佳位置,记为gbest=[pg1,pg2,…,pgN]。对于每一个粒子,其D维的速度和位置更新式分别为

(8)

(9)

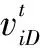
2 基于改进粒子群优化的构型优选

2.1 自适应惯性权重

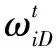
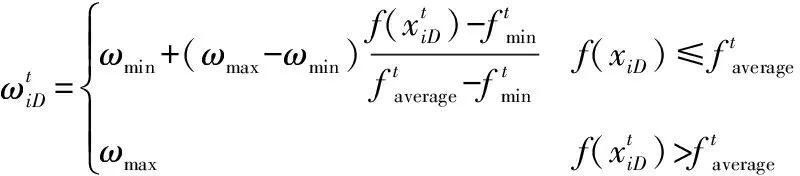
(10)

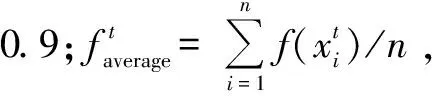
对于适应度函数较大的粒子,其筛选出的空间构型远离最优解,此时更需要进行全局搜索;对于适应度函数较小的粒子,其筛选出的空间构型与最优解接近,此时要进行局部搜索,让粒子向更好的搜索区靠近,从而筛选出最优的空间构型。

2.2 非对称学习因子

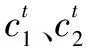
(11)

(12)

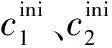
由式(11)、式(12)可以看出,随着迭代次数的增加,c1线性递减、c2线性递增,从而加强了粒子向全局最优构型的筛选能力。

2.3 改进粒子群优化算法适应度函数

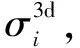
(13)

2.4 改进粒子群优化算法步骤

在进行信息融合之前,筛选出最优的协同构型,从而依靠部分锚机的协同信息进行定位,能在保证精度的同时大幅提升导航解算的速度。采用改进的粒子群优化算法对集群无人机协同导航构型进行优选,算法的流程如图2所示。

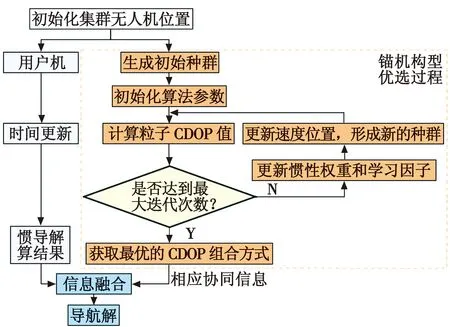
图2 改进粒子群优化算法流程图Fig.2 Flow chart of improved particle swarm optimization algorithm

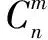
3 仿真分析

3.1 仿真条件

本文以31架集群无人机组成的编队系统为例,进行了集群无人机编队飞行协同导航仿真。其中,1架无人机为卫星不可用下的用户机,其余30架无人机为卫星可用下辅助用户机进行导航的锚机。设定集群无人机中的所有无人机都可以进行测距和通信,其位置分布如图3所示,在众多锚机的协同信息中,用户机筛选其中4架无人机的信息进行导航定位。图4为集群无人机的飞行轨迹。

图3 集群无人机分布Fig.3 Distribution of clustered UAVs

表1列出集群无人机的机载传感器参数配置,其中,GNSS导航输出误差、UWB测距误差均设置为高斯噪声。

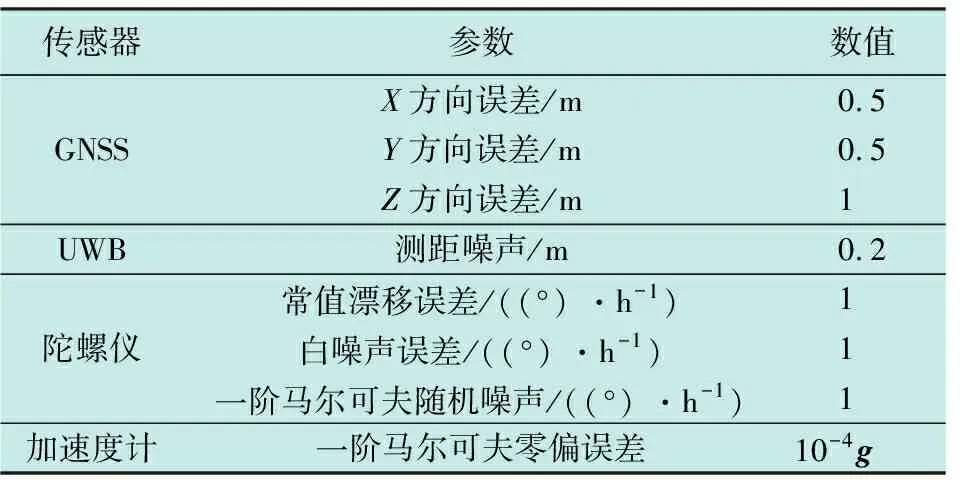
表1 集群无人机传感器参数配置

3.2 仿真结果分析

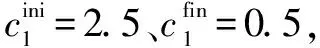
图5 算法迭代曲线Fig.5 Algorithm iteration curves

从图5中可以看出,通过在粒子群寻优阶段引入自适应的惯性权重和非对称的学习因子,扩大了粒子的搜索范围,提高了算法的全局搜索能力,改进后的粒子群优化算法的收敛速度和寻优性能都优于另外两种算法。

为了进一步验证本文算法的有效性。设计了4种情况进行对比实验。1) 本文算法:采用改进粒子群优化算法优选出4架锚机与用户机进行协同定位。2) PSO:采用经典的粒子群优化算法优选出4架锚机与用户机进行协同定位。3) 快速选星:采用基于高度角和方位角的快速选星优选进行协同定位。4) 随机选取:在集群无人机中随机选取4架锚机与用户机进行协同定位。

由此可以得到如图6所示的4种情况下用户机定位误差对比曲线。

图6 定位误差对比曲线Fig.6 Positioning error contrast curves

由图6可知,采用随机选取方法时,由于选取的不确定性导致定位误差较大,采用快速选星能提升选星速度,但其定位精度不能保证,而采用本文所提出的改进粒子群优化算法,3轴定位误差均明显小于对比算法,提高了用户机的三维定位精度。

在此基础上,与不进行构型优选时用户机融合所有30架锚机的协同信息进行导航定位的算法进行对比,结果如图7所示。

图7 三维定位误差对比曲线Fig.7 3D positioning error comparison curve

为了对5种算法的三维定位误差精度进行定量的分析,计算5种算法下用户机的三维位置均方根误差(RMSE),结果如表2所示。

表2 三维位置误差统计结果

由图6、图7和表2可知,本文算法具有较小的RMSE误差,定位精度更接近融合所有锚机时的定位精度,相比于PSO、快速选星和随机选取算法时误差更小,稳定性更好。

此外,为了验证本文算法的运算效率,将本文算法、PSO算法以及不进行构型优选的算法各进行50次仿真,得到相应的运行时间如表3所示。

表3 不同算法运行的时间性能对比

由图6、图7和表3可以看出,本文算法与不进行构型优选并融合所有锚机的算法相比精度略低,但优于随机选取算法和经典PSO算法,更重要的是,本文算法的运算效率得到了大幅提升,能够更好地满足集群无人机协同定位解算的实时性需求。

4 结论

本文首先利用CDOP作为构型评估标准。在此基础上,通过自适应调整惯性权重以及采用非对称的学习因子对传统粒子群算法进行了改进,提高了算法的寻优能力和全局收敛能力。仿真结果表明,本文提出的改进粒子群优化算法通过筛选出的锚机最优构型与用户机之间进行协同信息交互并辅助用户机进行定位,相较于现有方法,本文的优选方法在定位精度和收敛速度方面均有所提升。在本文方法基础上筛选出的锚机最优构型与用户机之间进行协同信息交互,辅助用户机进行定位。本文的优选方法提高了集群中用户机的定位精度,有效保证了卫星不可用下集群无人机的协同导航运算效率。