航发叶片机器人磨削颤振检测方法*
2024-05-08李鹏伟戴士杰张文华母嘉恒胡天荣
李鹏伟,戴士杰,张文华,母嘉恒,胡天荣
(河北工业大学,天津 300400)
随着机器人智能控制与各个学科的交叉融合,在航空发动机叶片表面磨抛中高效率、高精度的机器人加工备受青睐。航空发动机叶片属于典型的薄壁结构零件,在机器人高速磨削加工中很容易发生颤振。机器人加工系统的颤振是发生在刀具和工件之间的相互振动,是一种复杂的弹性动力学现象,主要由机器人加工系统整体结构从周期性切削力中吸收能量自激产生[1]。颤振不仅会造成磨削力波动,而且会严重降低加工表面质量[2]。为了防止颤振对磨削系统破坏,早期、快速、准确的颤振检测至关重要。
颤振检测的过程主要分为3部分:数据采集、特征提取、状态识别[3]。其中,在颤振信号的数据采集过程中,可以利用各种加工信号,例如,声音信号采集简单可靠,但容易受到外界噪声的影响;力信号对切削状态的变化反应迅速,但传感器安装位置的选择比较困难;加速度信号对振动的表现最为直观,但采集加速度信号需要昂贵的仪器[4-7]。在颤振信号的特征提取过程中,可以利用信号处理的方法构造特征指标,该指标为后期定义颤振判据提供理论依据。Chen等[8]依靠数据处理算法,从提取的多个特征参数中自动选择有效的颤振识别特征参数。Yao等[9]利用颤振信号的小波变换标准差和小波包变换能量比作为二维特征向量进行颤振检测。在颤振的状态识别过程中,实时性是颤振识别的一个重要要求,这意味着颤振应该事先被识别出来。Chen等[10]提出一种基于EEMD和特征选择的多通道颤振智能检测策略,但烦冗的计算量会导致系统实时性较差。Li等[11]通过经验模态分解成功提取颤振识别的特征向量,该方法用时不足1 s。
目前,关于加工颤振检测的研究主要围绕铣削、车削等展开,而较少关注机器人磨削[12],而且大部分检测方法仍然不能在工件损坏之前识别颤振,达不到防止工件损坏的核心目标。因此,本文提出一种基于排列熵的机器人磨削颤振检测方法:首先,采集机器人末端的颤振加速度信号;然后,利用滑动窗口算法从原始信号中提取连续的排列熵值;最后,通过排列熵经验阈值判断末端执行器是否发生颤振。在此过程中,采用基于序数模式的排列熵算法,利用序数模式及其分布规律,简化了排列熵计算过程,提高了排列熵特征的计算效率。仿真和试验结果表明,排列熵值的骤降时刻远远早于颤振完全产生时刻,说明该方法能够在颤振孕育过程的初始阶段检测出颤振,为后续采取抑制措施提供更多的反应时间。
1 基于序数模式的排列熵
1.1 序数模式
序数模式描述了时间序列相邻值之间的顺序关系。可设时间序列 (xm,xm-t,…,xm-dt) 的d阶序数模式为序数模式的计算表达式为
式中,m为时间序列中数据的数量;h=1,2,…,d;t为时间延迟,代表相邻序数模式的中点间的距离;d为阶数,代表一个序数模式中含有(d+ 1)个数据。
通过给每一种序数模式分配代号,可以更加方便地观察序数模式的分布情况,其中代号按式 (2)进行一对一的分配。
例如,当阶数d= 2时,会产生6种序数模式类型,分别对应数字代号“0、1、2、3、4、5”,如图1所示。
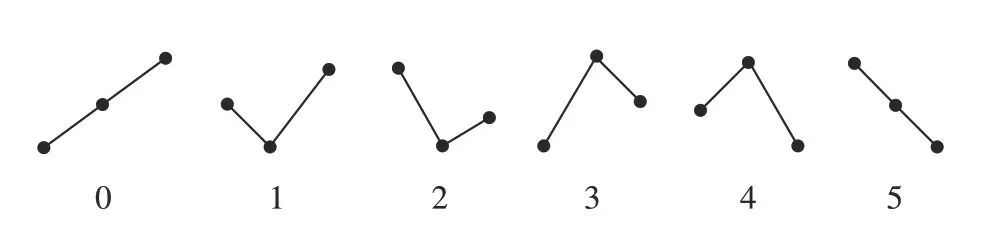
图1 d = 2时序数模式的类型Fig.1 Types of ordinal patterns at d = 2
1.2 基于序数模式的排列熵计算
排列熵是一种衡量时间序列复杂程度的特征,能够准确地定位系统发生突变的时刻,可以对突变信号的微小变化时刻进行放大。
滑动窗口内的时间序列 (xm,xm-1,…,xm-M-dt+1) 在时间延迟t和阶数d下的排列熵可以根据式 (3)进行计算。
式中,M为窗口中存在的序数模式的数量;qj= #[k∈{m,m-1,…,m-M+ 1}|(xk,xk-t,xk-dt)存在序数模式j]。
设由10个值组成的时间序列为 (x1,x2,…,x10),此时间序列中时间延迟t= 2、阶数d= 2的序数模式如图2所示。
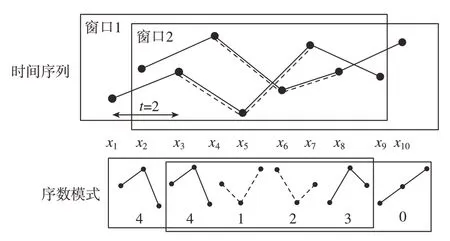
图2 滑动窗口中的序数模式Fig.2 Ordinal patterns in the sliding window
由图2可知,两个窗口存在4种序数模式的“重叠”部分。根据式 (3)可在窗口1和窗口2中相应地求得排列熵(9)和(10),即
1.3 高效计算连续序数模式
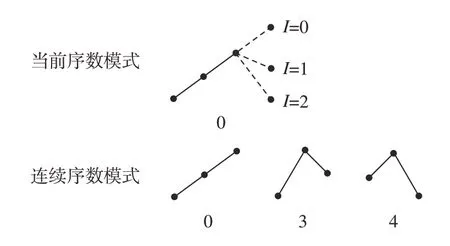
图3 序数模式“0”以及其连续序数模式的可能类型Fig.3 Ordinal pattern “0” and its possible types of consecutive ordinal patterns
由图3可知,对于序数模式“0”的下一个值有3个可能的位置,则下一个连续序数模式有3种可能的类型:“0、3、4”。
同理可得,可以对其他阶数的给定序数模式的下一个连续序数模式的可能类型进行分析。当前序数模式已知,通过下一个数据与当前序数模式中数据的大小比较,可求得下一个序数模式的类型,如式 (4)所示。
式中,ωd表示根据当前序数模式来确定下一个序数模式的函数;I表示 (xm,xm-t,…,xm-(d–1)t)中有多少个值大于或等于xm+t。
根据式 (4)和 (5),可以求得所有阶数序数模式的连续序数模式。d=2阶的序数模式及其连续模式如图4所示。例如,对于序数模式“0、1、2”,下一个值有3个可能的位置“I= 0、1、2”,也就有3个可能的连续序数模式“0,3,4”。对于序数模式“3、4、5”,下一个值有3个可能的位置“I= 0,1,2”,也就有3个可能的连续序数模式“1,2,5”。同理可得,每个代号为 (d+1)(k-1),…,(d+1)k-1的序数模式具有相同的连续序数模式,其中k=1,2,…,d!。根据上述方法,可以求得所有的序数模式以及其连续序数模式。
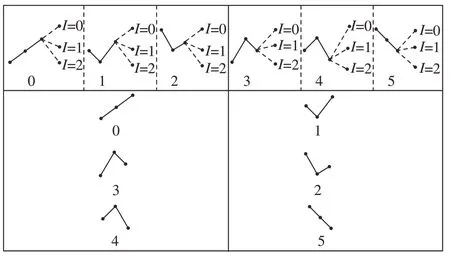
图4 阶数d =2的所有序数模式以及其连续序数模式Fig.4 All ordinal patterns of order d =2 and their consecutive ordinal patterns
排列熵是在具有最大重叠的大小为M的滑动窗口中计算的,即连续窗口的第1个值是前一个窗口的第2个值。连续的窗口 (xm-1,xm-2,…,xm-M-dt)和 (xm,xm-1,…,xm-M-dt+1)在值xm和xm-M-dt上有所不同,因此窗口中的序数分布在序数模式(m)和(m-M)的出现频率上有所不同。所以在已知排列熵(m-1)的情况下,排列熵(m)的计算方法可表示为
1.4 基于序数模式的排列熵的计算效率
本文提出的基于序数模式的排列熵计算方法通过比较信号数据中相邻数值的大小确定序数模式的类型(序数模式类型的定义已经给出)。利用图4的序数模式分布规律可快速获得连续的序数模式分布情况。最后通过连续序数模式的类型,以及式 (1)~(6)计算基于序数模式的排列熵值,并利用滑动窗口算法得到连续的基于序数模式的排列熵值。
分别利用传统排列熵算法和所提出的基于序数模式排列熵算法对不同信号长度以及不同阶数的随机信号进行分析,然后对两种算法排列熵提取的计算时间进行比较 (计算时间是多次运行的平均值),结果如表1所示。
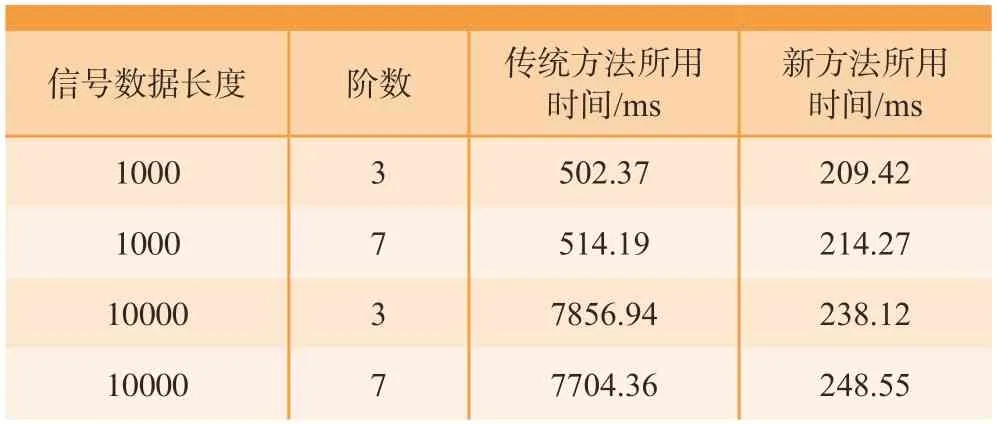
表1 不同方法计算排列熵值的执行时间Table 1 Execution time for calculatating permutation entropy using different methods
由表1可知,当原始信号长度加倍时,两种计算方法的执行时间都有所增加。然而,相比于传统排列熵计算方法,基于序数模式排列熵计算方法的计算时间要低于一个数量级。因此,基于序数模式的排列熵计算方法效率更高,更有利于实现颤振的及时检测。
基于序数模式的排列熵方法对上述有效计算进行总结,计算方案如图5所示。其中,W为时间序列的长度。
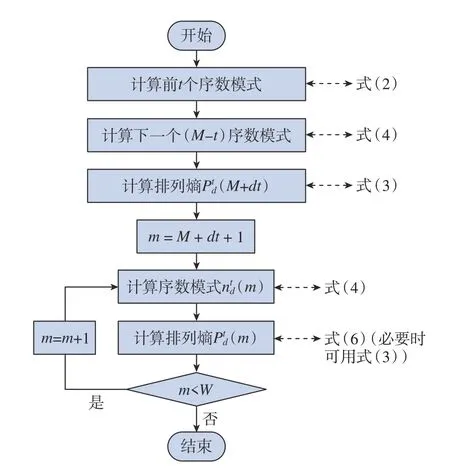
图5 基于序数模式的排列熵计算方案Fig.5 Permutation entropy calculation scheme based on ordinal pattern
2 仿真算例分析
颤振的发生一般有3个阶段,即平稳阶段、过渡阶段和颤振阶段[13]。颤振信号通常表现为单次谐波特征,因此,当颤振发生时,加速度信号可用单频谐波函数描述。为了验证所提出的磨削颤振检测方法的有效性,现利用仿真软件,直观地表达出颤振从稳定到不稳定逐步发展的过程,且将存在平稳、过渡和颤振3个阶段的颤振信号模拟出来,颤振加速度模拟信号如图6所示。
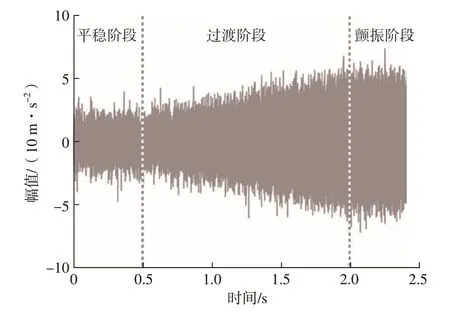
图6 经历平稳、过渡和颤振阶段的加速度模拟信号Fig.6 Simulated acceleration signal through smooth, transition and chatter phases
本研究选取阶数d= 3,时间延迟t= 1,滑动窗口大小M= 512对颤振原始信号进行窗口滑动计算,每次对每个窗口范围的信号进行一次排列熵值计算,最终得到连续的排列熵值数据,可以更直观地观察加速度信号变化与排列熵值变化的差异对比情况。滑动窗口算法计算出基于序数模式排列熵的动态变化情况如图7所示。
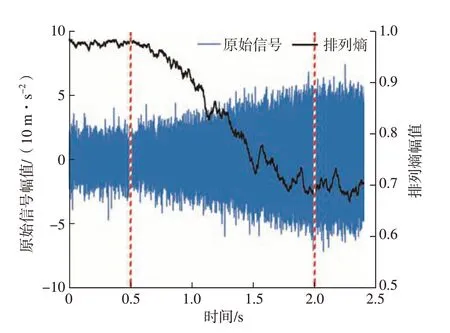
图7 颤振信号的排列熵特征Fig.7 Permutation entropy characteristics of chattering signal
由图7可知,在平稳阶段的排列熵特征曲线大致保持在水平稳定状态。由于周期性振动的积累,颤振逐渐产生,排列熵特征曲线发生骤降,而且骤降发生在颤振过渡阶段的前期。排列熵特征骤降可以作为颤振即将发生的征兆,而且排列熵骤降时刻要远远早于颤振完全产生时刻,因此可以利用排列熵骤降作为颤振检测的特征。
3 试验验证
3.1 试验平台搭建
本节通过航空发动机叶片机器人磨削试验来验证本文所提出的磨削颤振检测的可靠性,试验平台的搭建如图8所示,加工工件是材质为镍基合金的航空发动机压气机叶片,磨具为粒度500目的柔性砂轮。

图8 航空发动机叶片机器人磨抛试验平台Fig.8 Robot grinding experimental platform for aero-engine blade
机器人磨削颤振信号采集装置如图9所示,相比于末端执行器,三轴加速度传感器的体积及重量极小,在此可忽略加速度传感器重量对末端颤振的影响。其他试验设备及相关参数如表2所示。
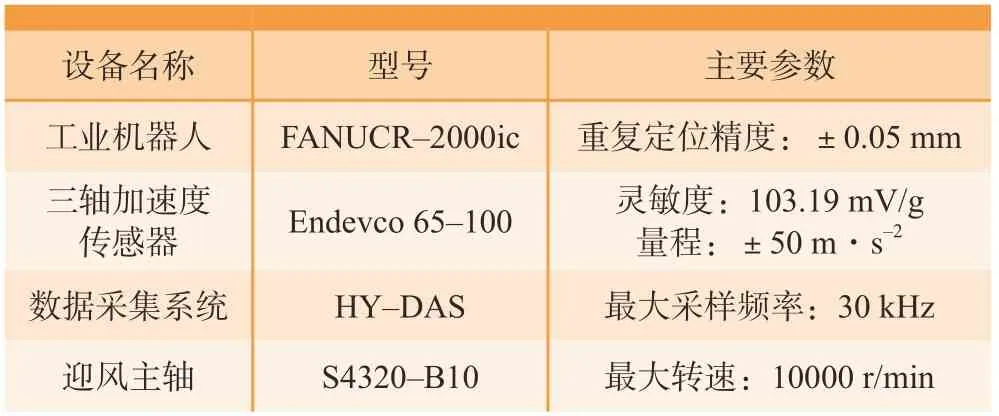
表2 试验设备及其主要参数Table 2 Experimental equipment and its main parameters

图9 机器人磨削颤振信号采集装置Fig.9 Acquisition device of chattering signal of robot grinding
3.2 颤振信号分析
通过改变磨削加工参数,采集机器人末端在不同加工状态下的颤振信号,磨削加工参数如表3所示。
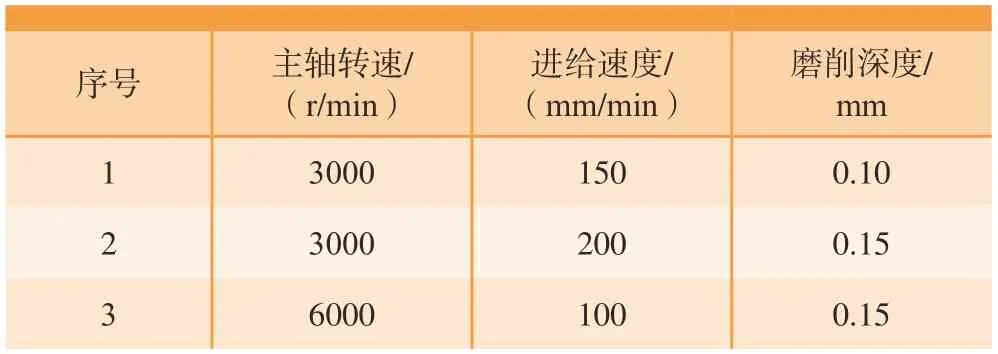
表3 试验中的磨削加工参数Table 3 Grinding parameters in the experiment
试验由安装在磨削末端执行器上的三轴加速度传感器测量颤振加速度信号,通过HY-DAS数据系统采集颤振加速度信号,采用上位机对颤振加速度信号进行实时排列熵提取。其中,利用本文所提出基于序数模式的排列熵算法进行磨削颤振检测,即选取阶数d= 3、时间延迟t= 1、滑动窗口大小M= 512提取排列熵特征。根据表3中的加工参数进行航空发动机叶片机器人磨削,在试验结果中选取几组代表性数据进行分析,得到颤振原始信号及其连续排列熵特征,如图10所示。
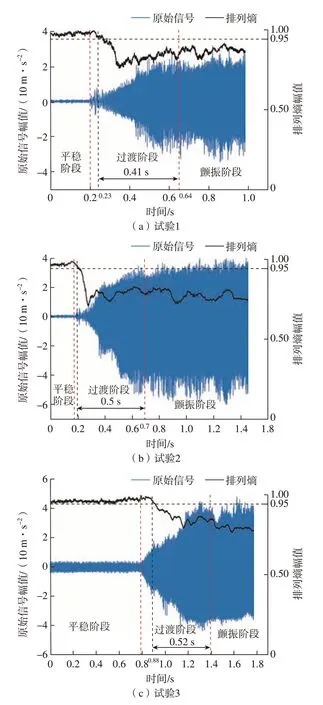
图10 颤振原始信号和排列熵Fig.10 Chattering raw signal and permutation entropy
图10(a)中排列熵值在0.23 s时低于0.95,早于颤振完全发生阶段0.41s;图10(b)中排列熵值在0.2 s时低于0.95,早于颤振完全发生阶段0.5 s;图10(c)中排列熵值在0.88 s时低于0.95,早于颤振完全发生阶段0.52 s。由此可知,排列熵值低于0.95时刻早于颤振完全发生时刻约0.48 s。
由图10可知,当颤振未发生时,排列熵特征处于水平稳定的状态。随着颤振的产生,原始信号幅值随之增加,在过渡阶段的初始位置,排列熵值发生骤降 (虚线为排列熵骤降时刻),此时即可判断出磨削过程中发生了颤振,而且排列熵值骤降时刻远远早于颤振完全产生时刻,即可以在较早阶段检测出颤振。因此以排列熵值的骤降作为颤振检测的标准,能够在颤振完全产生前0.48 s检测出颤振,为磨削系统采取颤振抑制措施提供更多的反应时间。该试验证明所提出的方法在机器人磨削颤振检测方面是有效的。
3.3 特征对比
基于振动信号时域分析理论,选取方差、裕度因子作为颤振检测的特征量来反映磨削颤振信号的变化趋势,利用滑动窗口算法提取方差、裕度因子特征曲线,并与排列熵特征进行对比,结果如图11所示。
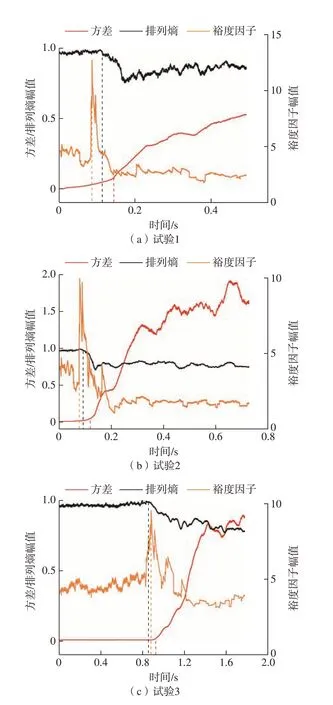
图11 颤振检测特征:排列熵、方差、裕度因子Fig.11 Features of chatter detection: permutation entropy, variance,margin factor
由图11可知,方差特征曲线会随着信号幅值的增减而增减,其变化受原始信号幅值的影响较大,而且方差特征曲线的变化幅度小于原始信号变化幅度,所以其检测准确性较差。裕度因子特征曲线变化不稳定,曲线波动范围较大,所以其检测精度较差。相比于方差和裕度因子,小波包熵特征骤降时刻要更早 (图11中的虚线为各个特征的转折时间点),而且其波动较小、变化稳定。
综上所述,排列熵特征对颤振发生的反应速度更快,因此利用排列熵特征能够更早地检测出颤振,为磨削系统采取颤振抑制措施提供更多反应时间。
3.4 颤振状态识别
颤振状态识别最简单的方法就是特征阈值法,通过对比某个特征量在平稳阶段与颤振征兆出现阶段的变化情况,设定一个经验型的阈值,一旦超过或低于预先设定的阈值则判定为出现颤振,即可提醒系统采取颤振抑制措施。根据图10中的排列熵特征的动态变化规律,可设置经验阈值为0.95,即当排列熵低于0.95则判定此时加工系统中发生颤振。
综上所述,机器人磨削末端颤振检测方法的流程如图12所示。首先设置磨削加工参数,利用机器人带动末端执行器进行航空发动机叶片磨削,并通过安装在末端执行器上的加速度传感器对磨削颤振信号进行采集;然后利用序数模式进行排列熵特征连续提取;最后当排列熵特征值小于0.95时,即判定此时机器人末端正在产生颤振,可为系统发出警告,提醒系统采取颤振抑制措施。
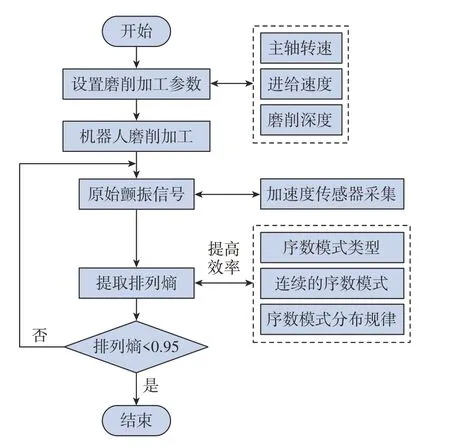
图12 颤振检测方法流程图Fig.12 Flow chart of chatter detection method
试验结果表明,当颤振信号加速度幅值刚开始增加时排列熵值就会发生骤降,因此,在过渡阶段的初始位置将颤振检测出来 (排列熵值低于0.95时即可认定此时的磨削过程中发生了颤振)为进行抑制操作提供了更多反应时间。
4 结论
针对航空发动机叶片机器人磨削颤振检测不及时导致颤振抑制滞后的问题,本文提出了一种基于排列熵的航空发动机叶片机器人磨削末端颤振检测方法。该方法通过对原始信号进行排列熵特征提取,并利用该特征进行颤振检测,当排列熵值低于0.95时,判定机器人末端正在产生颤振,立即向系统发出警告,提醒系统采取颤振抑制措施。
针对实时性要求,采用基于序数模式的排列熵算法对颤振原始信号实时计算排列熵,该方法相较于传统排列熵算法计算时间减小了一个数量级,当信号长度为10000时,基于序数模式排列熵算法的计算时间约为0.25 s。
最后,试验结果表明,通过排列熵特征提取算法的改进,基于排列熵的航空发动机叶片机器人磨削末端颤振检测方法能够在颤振爆发前约0.48 s检测出颤振,可及时向系统发出警告,为后续采取措施提供了更多的反应时间。
目前本文中排列熵特征阈值的应用范围有待进一步拓展,后续还需进一步研究状态识别阈值的自适应选择标准。
