基于粒子群优化算法的柔性生产线排产方法
2024-05-08玉海龙
玉海龙,何 陶
(航空工业成都飞机工业(集团)有限责任公司,成都 610092)
根据前瞻产业研究院的研究报道[1],在未来十年期间,绝大部分的老旧机型将会在更新换代中退役,新一代的先进机型也将会随之列装。在军工产品型号升级换代速度快、生产效率要求高、飞机数量需求大的当下,根据长期经验进行生产排产的传统排产方式很难使车间的生产效率达到最优。
为了适应中小批多品种的生产线排产与调度需求,在20世纪70年代,柔性制造系统 (Flexible manufacturing system,FMS)[2]应运而生。其中最关键的便是作业车间调度问题 (Job-shop scheduling problem,JSP),该问题的定义为:有一组机器需加工一组工件,每一个工件的加工由具有先后顺序约束的加工工序组成,每一个工序只需要一台机器来加工,且机器一直可用,机器可以在不被中断的情况下一次处理一个工序。在这样的条件下,决策的内容为如何对机器上的工序进行排序,使得完工时间最短[3]。在JSP的基础上,还有柔性作业车间调度问题[4](Flexible job-shop scheduling problem,FJSP),其减少了工序对机器的约束,即每一个工序可以由一台或者多台机器进行加工,更加贴近实际生产,同时也增加了问题的复杂度,是一个更加难求解的非确定性多项式时间难题[5]。
为了解决调度问题,国内外学者研究并提出了多种算法,较早研究FJSP问题的是Bruker[5],他于1990年提出了求解只有2个工件的简单FJSP的多项式算法;Lin等[6]将遗传算法与粒子群算法相结合,提出混合演化算法;Xia等[7]采用粒子群算法与模拟退火算法相结合的方法对多目标FJSP进行求解,不仅提高了算法的效率,还提高了求解的质量;Teekeng等[8]提出一种改进的遗传算法,他们采用“模糊轮盘赌选择”的方式改进交叉算子和变异算子的计算,使遗传的种群保持了种群的多样性,克服了收敛过早的问题。
经过实际应用测试分析发现,传统的遗传算法和粒子群算法并不能实际解决本文生产线排产问题,为此,本文对粒子群算法进行求解优化,最终实现对文中排产问题的求解。
1 柔性生产线分析与建模
1.1 柔性生产线分析
零部件加工柔性生产线由物料库、物料机器人及导轨、上下料工位、加工机床、测量机、总控台、刀具机器人及导轨、刀具更换工位、刀具库组成,如图1所示。其中MT1、MT2是4轴数控加工机床,MT3、MT4是5轴数控加工机床。
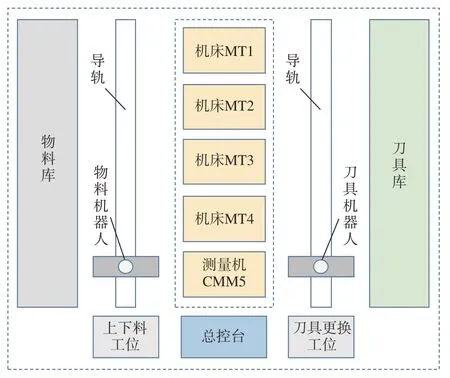
图1 柔性生产线布局图Fig.1 Layout drawing of flexible production line
该生产线中的机床和测量机均具备双工作台,即加工区和准备区,通过双工作台可以实现机床和测量机不间断更换工件,减少物料更换与等待时间。但在以下情况发生时,需要考虑物料机器人搬运时间,即当某工件刚完成加工且该工件需要测量,而此时测量机处于空闲状态,物料机器人将直接从机床上取料,然后送往测量机进行测量,此时需要考虑物料机器人搬运时间,该时间平均约为1 min。机器人给各个机床和测量机上料与下料的时间大约也是1 min。
根据柔性生产线的实际生产任务,其调度需求如下。
(1)紧急插单。即在原定的计划中添加新的订单,并且该订单需要被优先加工。
(2)任务指定机床。在进行生产计划制定的时候,将某一个加工任务指定到某一台或者一类机床上进行加工,指定到某一台机床通常适用于操作人员调试新品工艺参数,而指定到某一类机床适用于只能使用某类机床进行加工的工件。
(3)机床热拔插。一种情况是在某一台机床不执行任务时,将该机床退出该生产线,通常适用于对机床的维修等工作;另一种情况是在需要增加生产线的产能时,新增机床。
(4)工件测量。在某些工件完成加工后,需要对其进行测量,通常适用于对精度、质量要求较高的产品,或者是首批加工的产品。
(5)工件暂停生产。根据生产或者用户的需要停止某些工件的生产。
(6)任务指定期限。有一些特定的工件,其需求时间是有要求的,针对这种情况,生产线在排产时需要实现其在指定期限内完成加工。
(7)加工效率最高。在满足所有加工条件约束的前提下,实现所有工件以最高效率完成加工与测量,即所有的加工任务完工时间最短。
1.2 生产线建模
1.2.1 通过任务优先级解决紧急插单问题
为实现有特殊工期要求的工件可以提前加工,对进入柔性生产线加工的工件设立优先级,在排产时,优先加工优先级高的工件。本文为工件设计3个优先级:普通等级、优先等级、紧急等级,对应的编码为1、2、3,其加工的优先级为紧急等级>优先等级>普通等级。
在排产时,为减少排产复杂度,提高资源利用率,仅考虑同一台机床上所加工的零件的优先级。例如A号机床分配到TK1、TK2、TK3、TK4 4个工件进行加工,它们的优先级依次为3、2、1、1;B号机床分配到4个工件TK5、TK6、TK7、TK8进行加工,它们的优先级依次为1、1、1、1。
本文仅单独考虑A号、B号机床上的4个零件,其优先级满足要求即可,并不要求B号机床上加工的第1个工件的优先级高于A号机床上加工的第2个工件。
1.2.2 机床约束
根据生产线的实际情况,工件任务对机床的约束可以分为4种情况:(1)只能在4轴机床上加工; (2)只能在5轴机床上加工; (3)可以在4、5轴机床上加工;(4)指定在某台机床上加工。
对于可以在两类机床上加工的工件,本文认为其在不同机床上加工的时间是相同的。
为了明确表示工件任务对应的机床以及加工时间信息,工件任务信息中关于设备属性的信息如表1所示。
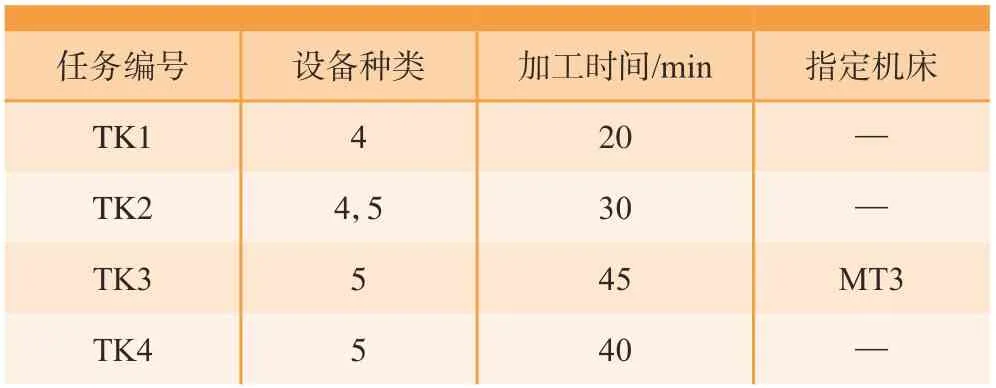
表1 工件任务设备信息表Table 1 Workpiece task equipment information table
1.2.3 刀具更换与冲突时间
一个工件的加工通常需要一个刀具集才能完成,为了方便分析,本文对刀具做如下设定。
(1)将工件任务所需的刀具集作为一个整体,在需要刀具时,将其以一个整体为单位运送到机床上。
(2)当下一个加工任务所需的刀具集不同时,需要将当前的刀具集全部移出,并换上新的刀具集。因此加工第1个工件时,默认需要进行一次刀具更换。
(3)当相邻的两个工件使用的刀具集相同时,无须更换刀具。
(4)由于刀具数量有限,设定一个刀具集只有一套,当某刀具集正在被使用,其他机床的工件若需要使用此刀具集,需等待该刀具集使用完毕。
(5)由于只有一个刀具更换机械手,当刀具更换时间冲突时,计算冲突机床的剩余加工时间,先给剩余加工时间最长的机床换刀;若剩余加工时间相同,则任务号小的先进行换刀。
(6)根据现场测试情况,刀具更换时间约为4 min。
1.2.4 工件测量顺序
柔性生产线上只有1台测量机,因此,本文设定所有工件均可以在该测量机上进行测量,工件测量顺序计算规则如下:
(1)首先根据任务完工时间对加工完成后的工件测量顺序进行排序;
(2)如果完工时间相同,则根据工件加工优先级进行排序;
(3)若完工时间与优先级均相同,则根据任务单的序号进行排序。
1.2.5 任务总超期时间
工件超期是针对完成时间有限定的工件任务而言的,任务总超期时间是所有任务超期时间的总和,设任务i的计划完工时间为Tpi,若无计划完成时间,则令Tpi=0。假设实际完成时间为Ti,则任务i超期时间TOi为
任务总超期时间Tover为
1.2.6 调度的目标
本文生产排产的调度目标是:在满足机床约束、工件任务优先级约束及所有工件不超期的情况下,任务总完工时间最短。
任务总完工时间Ttotal为所有任务完成加工与测量后的时间。假设任务i的完成时间Ti对应的机床加工完成时间为Pi,测量完成时间为Mi,对于不进行测量的工件,令Mi= 0。任务总完工时间是最后一个工件完工时间。有
式中,n为任务数量。
2 排产算法设计与优化
2.1 工件任务信息描述
有20个工件加工任务,需要将其分配到柔性生产线的4台机床和测量机中进行加工和测量,其机床加工约束要求、加工时间、测量要求以及测量时间、加工刀具集合类型、完工时间要求以及加工优先级见表2。
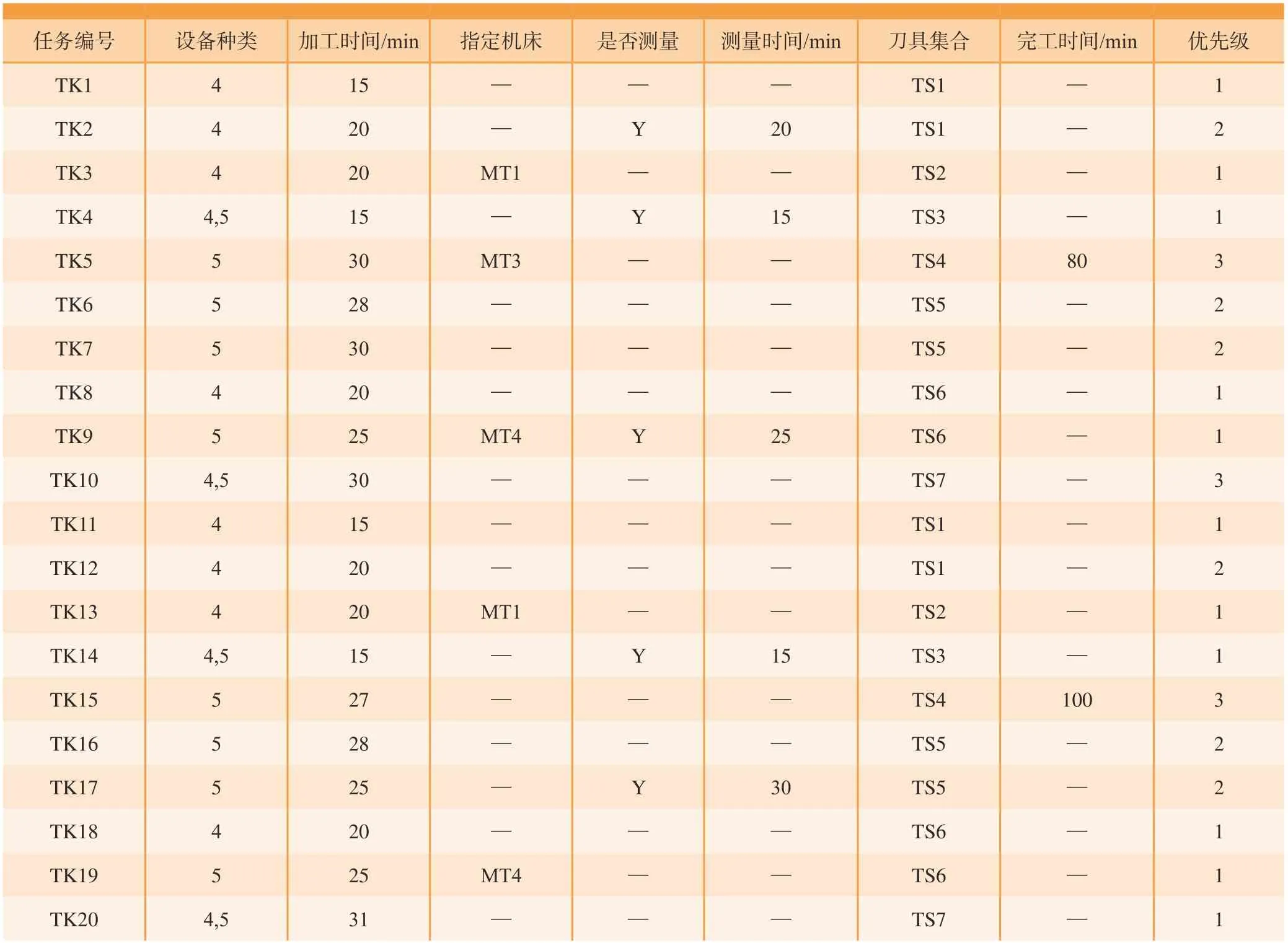
表2 工件任务信息表Table 2 Job task information table
2.2 排产算法设计
2.2.1 粒子群算法简介
粒子群优化 (Particle swarm optimization,PSO)算法在连续域内寻优表现出良好的求解性能[9],通过适当的编码规则,PSO同样也可以应用在某些离线域的寻优求解上,例如调度问题[10-12]。因此,本文选用粒子群算法作为核心算法,求解柔性生产线排产调度问题。
粒子群优化算法流程图如图2所示,其种群迭代退出条件是达到最大的迭代次数或者全局最优位置满足最小界限。
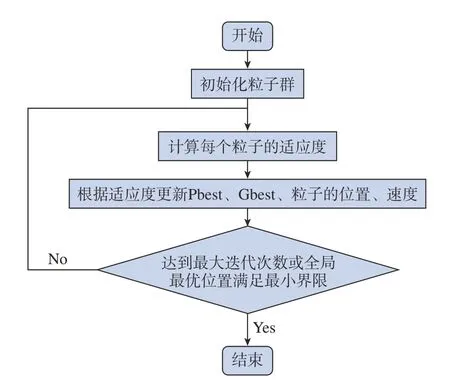
图2 粒子群优化算法流程图Fig.2 Particle swarm optimization algorithm flow chart
其中粒子速度和位置的更新公式为
2.2.2 粒子编码
针对柔性生产线实际排产任务,可进行粒子编码,即假设总加工任务为N,则其可行解为一个2N的行向量,向量中包含了N个任务的加工顺序及各个任务对应的N个加工机床。粒子群优化算法中,将该可行解定义为粒子P,其包含PMT[N]以及Ptask[N]。其中Ptask[N]是任务向量,由N个1~N之间的不重复的正整数组成;PMT[N]是机床向量,是由N个1~M(不包括测量机在内的机床总数)之间的正整数组成。
为了说明粒子含义,本文随机构造一个粒子,即
Ptask[N]:[4,5,9,10,1,2,3,6,8,12,7,15,11,13,16,17,18,20,19,14]
PMT[N]:[1,2,4,2,3,2,1,4,2,3,1,4,2,3,4,2,1,3,1,4]
Ptask[N]中各个序号代表任务数,PMT[N]中各个序号代表加工的机床。由此可以得到任务与机床的对应关系如表3所示。
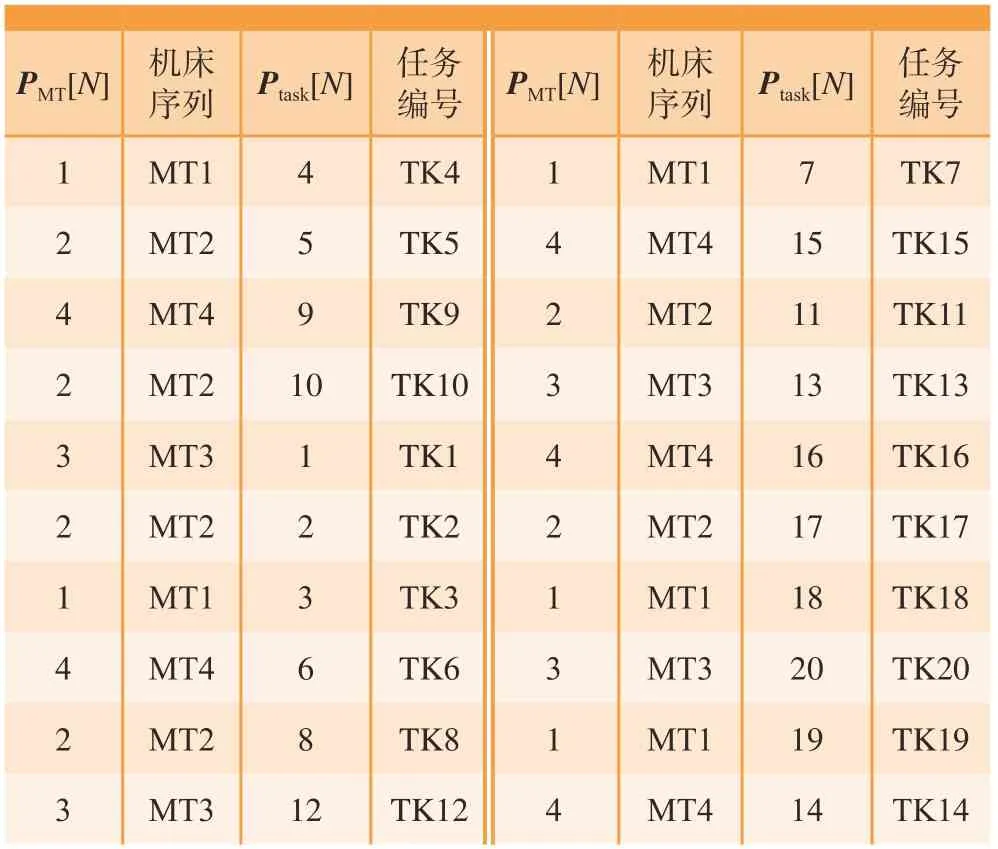
表3 通过粒子获取的机床与任务的对应关系表Table 3 Correspondence between machine tools and tasks obtained through particles
2.2.3 适应度定义
根据生产线模型可知,本文对任务的要求是多方面的,它包括任务总完工时间Ttotal、任务总超期时间Tover、机床约束积分SMT以及任务优先级约束积分SPr。本文根据生产实际需要,将这4个要求定义了如下的重要等级:SMT(x)>Tover(x)>SPr(x)>Ttotal(x) 。
设定粒子x的适应度函数为F(x),则有
F(x)=SMT(x)/Tover(x)/SPr(x)/Ttotal(x)
适应度函数值越小,则该粒子的解越好。
根据粒子假设和对应关系可对任务增加机床约束,本文对机床约束采用积分方式判断排产后机床约束符合情况,当发现有一项任务不满足要求时,积分加1,可得表4所示对照表。
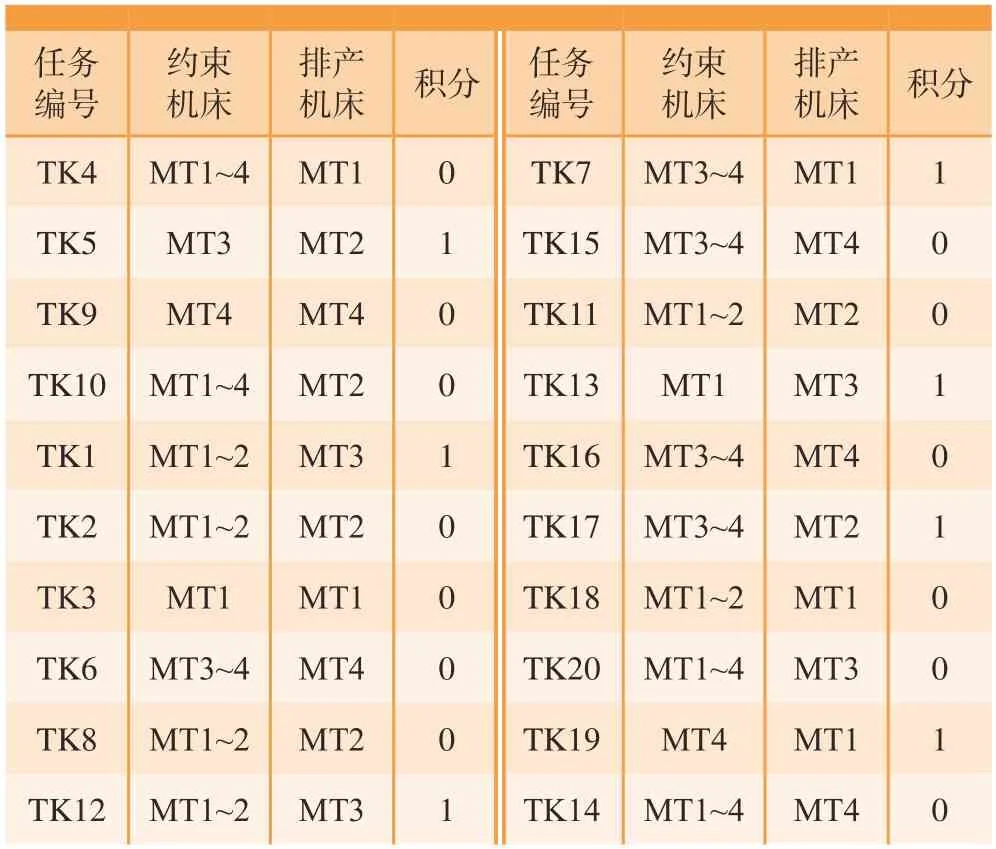
表4 任务与排产机床对照信息Table 4 Control information between tasks and production scheduling machines
只有当排产积分S= 0时,该排产才是有效的,才是可行解。
同时任务还有优先级顺序,因此对每一个机床上加工任务采用积分SPr的方式进行验证,最后将所有机床的积分相加,得到的分值为该排产计划的任务优先级约束积分。
积分规则为:设第j个机床上的第i个任务的优先级为,第j个机床的积分为。将与(0
其中,
n为j机床上加工分配到的任务数量。
排产计划的总得分SPr为
式中,NMT为机床数量。
根据式 (9)可分别计算得到MT1~MT4机床的任务优先级积分,即
总积分为9。
2.2.4 更新策略设计
根据更新公式 (式 (5)和 (6))及机床约束、任务优先级约束,可得具体迭代过程如下。
位置向量是由任务向量Ptask[N]和机床向量PMT[N]组成,速度向量也可以表示为任务更新速度向量Vtask[N]和机床更新速度向量VMT[N]。
任务共有N个,因此任务更新速度向量Vtask[N]的最大速度取[-N/2,N/2]之间,任务更新速度向量初始值通过随机数获取,计算公式为
机床更新速度向量VMT[N]同理,最大速度取[-NMT/2,NMT/2]之间,NMT为机床数量,其初始值计算公式为
由于机床向量PMT[N]的取值范围必须在[1,NMT]之间,因此对更新后的[N]向量的处理方法是首先进行四舍五入取整,再对超过边界值的数值,取对应的边界值。
而任务向量Ptask[N] 的取值是[1,N]之间不重复的正整数,为此采用排序映射法求取更新后的任务向量。具体过程为:
(1)记录原各个任务对应的向量序号;
(2)根据更新公式,计算获取下一代任务序列;
(3)将任务序列从低到高进行排序;
(4)提取排序后的任务序列对应的向量序号,作为新的任务序列。
2.3 算法性能测试
通过MATLAB对粒子群算法以及生产线模型进行实际测试的种群数量为80个,迭代次数为50次,学习因子c1= 2,c2= 2,惯性权重w= 0.75,运算10次,测试结果如表5所示。
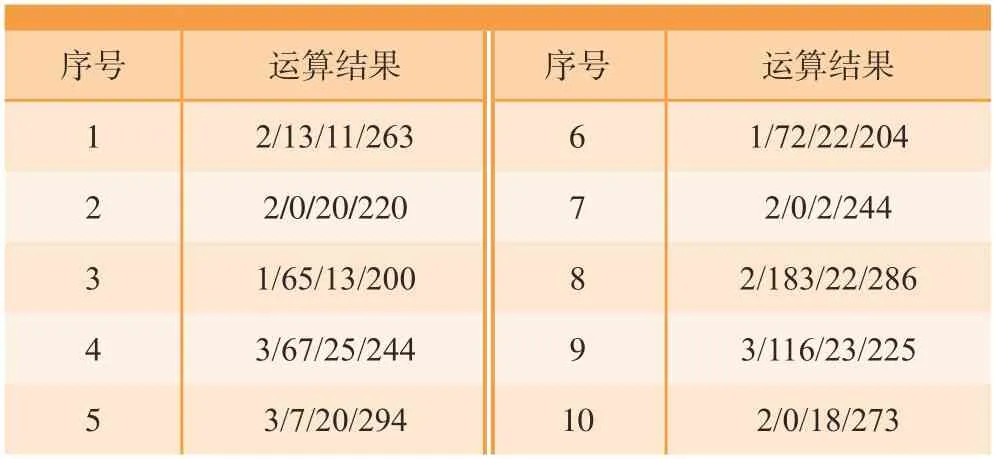
表5 测试结果Table 5 Test results
由运算结果可以看出,使用没有经过改进的粒子群算法对工件任务进行排产,所有的排产结果均不能满足机床约束和任务优先级约束的要求。
2.4 排产算法优化
根据生产线模型以及适应度函数的定义,可以发现本文研究的FJSP问题属于多目标优化问题,需要同时最小化4个目标,即任务总完工时间、任务总超期时间、机床约束积分以及任务优先级约束积分。根据文献[13]可知,虽然PSO算法在进行搜索时,可以一次性搜索解空间中的多个解,具有较好的并行计算能力,但是PSO算法的性能会随着问题规模的增大而降低,粒子飞行速度也会在算法的迭代过程中逐渐减小,最终会陷入局部极值而停止搜索。
根据上述分析可知,求解失败是因为求解目标过多,导致问题规模过大,最终在局部极值时收敛。因此,可通过减少粒子群优化算法的求解目标来降低问题规模,实现对FJSP问题的求解。
本文减少的求解目标为机床约束积分与任务优先级约束积分,保留任务总完工时间和任务总超期时间。
生成粒子时,工件将会分配到机床上,此时通过查询工件任务信息表即可知道工件是否符合机床约束的条件,若不符合约束要求,则对粒子进行调整,使其满足要求。调整规则如下:
(1)工件任务对机床的约束为“只能在4轴机床上加工”时,随机选取一个4轴机床作为工件任务的加工机床;
(2)工件任务对机床的约束为“只能在5轴机床上加工”时,随机选取一个5轴机床作为工件任务的加工机床;
(3)工件任务对机床的约束为“指定在某台机床上加工”时,将工件任务的加工机床设置为指定的机床。
通过上述规则调整后获得粒子的机床约束都满足要求,以此减少了“机床约束积分”求解目标。
为使工件的优先级满足要求,通过以下规则对机床的加工任务序列进行调整:
(1)将工件优先级从高到低重新排序,生成新的序列;
(2)当前后工件的优先级相同时,不对工件的前后位置关系进行调整。
通过上述规则调整后获得的粒子的优先级约束都满足要求,以此减少了“任务优先级约束积分”求解目标。
3 算法仿真结果
通过MATLAB对优化后的粒子群算法进行实现,以上述任务为对象,进行算法的性能、效率与可行性验证。
第1次测试的种群数量为60个,迭代次数为50次,学习因子c1= 2,c2= 2,惯性权重W= 0.75,运算10次,结果如表6所示。
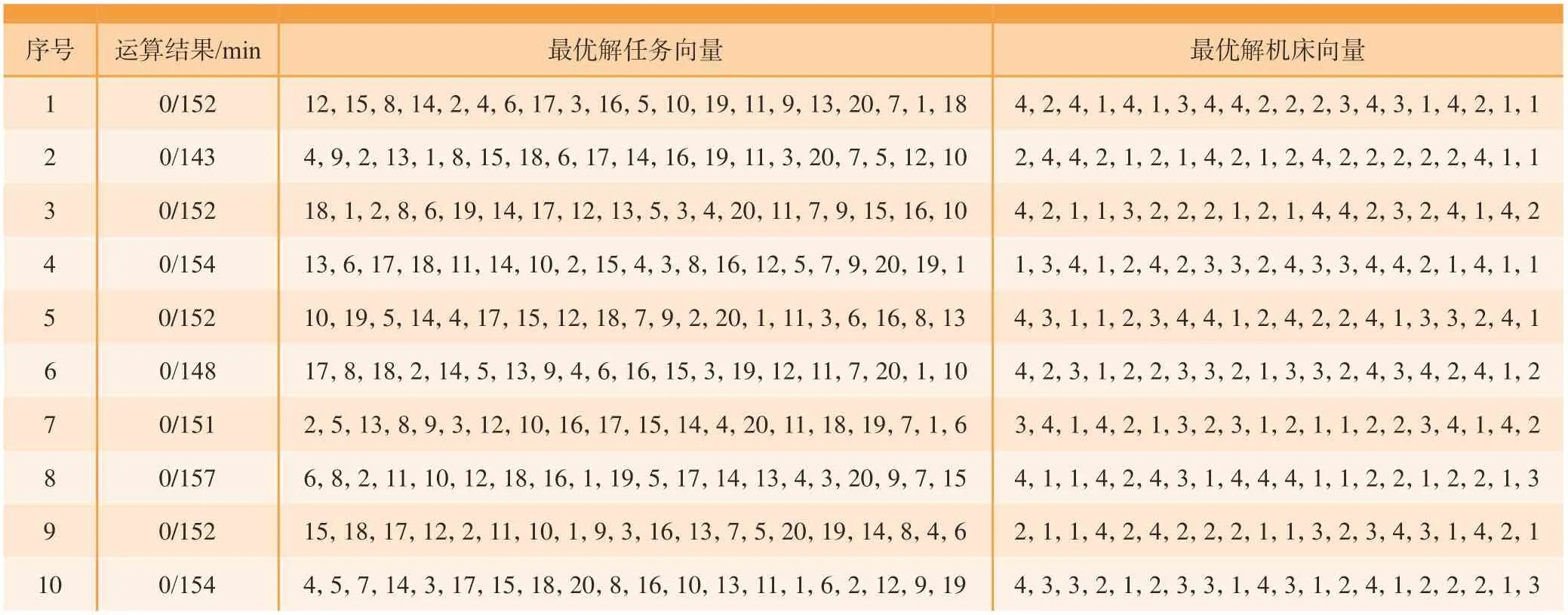
表6 优化后的算法第一次测试结果Table 6 First test results of optimized algorithms
表6中运算结果按照“任务总超期时间/任务总完工时间”进行呈现,如“0/152”表示任务总超期时间为0 min,任务总完工时间为152 min;其中的最优解任务向量与最优解机床向量共同构成一个解向量。
10次运算中的最优结果为“0/143”,其收敛过程如图3(a)所示,可以看出,总完工时间最初为163 min,经过27次迭代后,收敛到143 min。
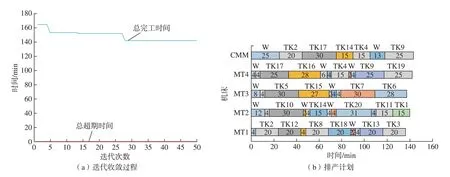
图3 最优结果“0/143”的收敛过程和排产计划Fig.3 Convergence process and production schedule of the optimal result "0/143"
图3(b)中“W”表示等待时间。机床MT1在生产过程中的总使用时间为136 min,其中刀具等待时间4 min、换刀时间12 min、执行机床加工时间120 min;机床MT2在生产过程中的总使用时间为140 min,其中刀具等待时间18 min、换刀时间16 min、执行机床加工时间106 min;机床MT3在生产过程中的总使用时间137 min,其中刀具等待时间14 min、换刀时间8 min、执行机床加工时间115 min;机床MT4在生产过程中的总使用时间为142 min,其中刀具等待时间12 min、换刀时间12 min、执行机床加工时间118 min;测量机的总使用时间为143 min,其中测量等待时间38 min、执行测量时间105 min。
第2次测试的种群数量为100个,迭代次数为100次,学习因子c1= 2,c2= 2,惯性权重w= 0.75,运算10次。其最优结果为“0/146”,收敛过程如图4所示,可以看出,总完工时间最初为163 min,经过37次迭代后,收敛到146 min。
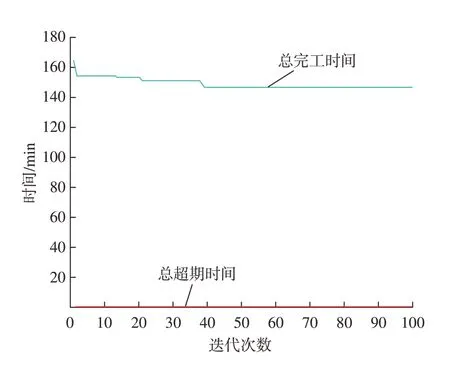
图4 最优结果“0/146”的迭代收敛过程Fig.4 Convergence process of the optimal result "0/146"
通过对比算法优化前与优化后的运算结果发现,优化后的所有最优解的超期时间均为0,因此所有的解均为有效解,获得有效解的概率为100%,而优化前的算法获得有效解的概率为0。由此可见通过较少求解目标以降低问题规模的优化方法对求解本文中生产线排产问题是可行的。
4 算法性能对比分析
为了测试改进后算法的性能,本节将改进后的算法与文献[14-15]中提出的改进PSO-GA算法和改进遗传算法进行比较。测试的对象为表 3所示的工件信息,优化目标同样为任务总完工时间Ttotal、任务总超期时间Tover、机床约束积分SMT及任务优先级约束积分SPr。使用的软件为MATLAB R2010b,系统运行环境为Windows 7 64bit,3.30 GHz CPU,20 G RAM。每个算法运行10 次,种群数量均为60个,迭代次数均为50次,其他参数采用文献中给出的典型值或最优值。从求解结果中选出较优的满意解。测试结果如表7所示。
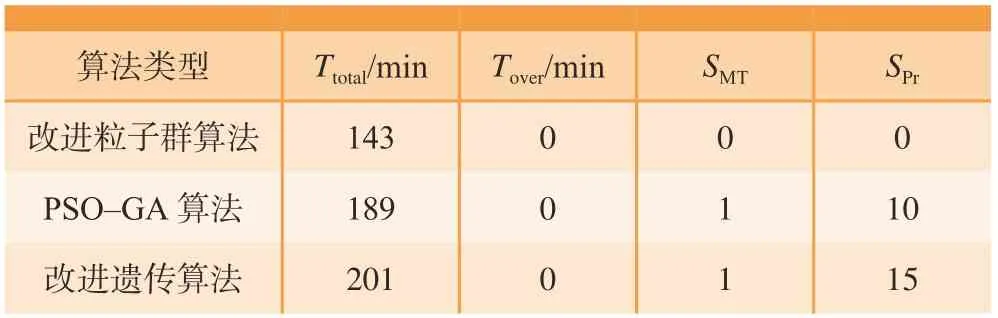
表7 算法性能对比结果Table 7 Comparison results of algorithm performance
从测试结果来看,文献[14-15]中算法的计算结果与改进前的PSO算法计算结果类似,均不能求解出满足机床约束和工件优先级约束的最优解。
5 结论
(1)以实际生产线为研究对象,分析调度需求,考虑工况中紧急插单、指定机床、任务优先级等情况,对生产线进行建模。
(2)提出一种带粒子调整环节的粒子群优化算法,在种群粒子初始化以及种群粒子更新后,新增粒子调整环节,在调整环节对粒子进行局部范围的定向编排优化,得到求解结果。
(3)设计了两组对比试验,试验结果表明,调整环节极大提高了排产算法的求解速度与求解质量,求解成功率为100%。
