双边定数截尾下线性指数分布的参数估计
2024-05-07邹路燕金良琼苏燕青李琼忆
邹路燕, 金良琼, 苏燕青, 陶 永, 李琼忆
(贵州民族大学 数据科学与信息工程学院, 贵州 贵阳 550025)
0 引言
指数分布是一种常见的寿命分布,其失效率为常数,当指数分布的失效率为时间的线性函数时,其寿命分布被称为线性指数分布(linear exponential distribution,LED).线性指数分布在μ=0时退化为指数分布,在θ=0时退化为瑞利分布,因此线性指数分布被认为是指数分布和瑞利分布的混合分布.众所周知,线性指数分布是用于寿命数据建模和故障率线性增加建模的分布.早在1958年,Broadbent[1]使用线性指数分布描述了牛奶瓶的寿命,之后也有一些学者对线性指数分布进行了研究.Fawzy[2]在逐步Ⅱ型删失下基于步进应力部分加速寿命试验讨论了线性指数分布参数估计问题,采用极大似然估计法和贝叶斯方法获得了该分布中参数和加速度因子的估计.隋云云等[3]根据截断删失试验样本,采用极大似然估计与EM算法对线性指数分布的参数进行估计,得到两种方法的参数估计效果接近,EM算法收敛的速度更快.Davies等[4]在逐步Ⅱ型删失竞争失效数据下讨论了线性指数分布的极大似然统计推断问题.
双边定数截尾数据是一种常见的截尾数据类型,因此也是一种不完全数据[5-7].该数据类型在进行寿命分析与可靠性分析时常常会遇到,因此有学者先后在该数据类型下进行了研究.侯华蕾等[8]在该数据类型下,选取未知参数的无信息先验分布和Gamma分布,分别在平方损失和Linex损失下,研究了Pareto分布的形状参数、可靠度以及失效率的Bayes估计.鄢伟安等[9]在该数据类型下,基于刻度平方误差损失与Linex损失,给出了广义指数分布中未知参数的Bayes估计与多层Bayes估计.王伟志等[10]在该数据类型下,研究了由Burr XII型部件组成的k(m)/n系统中未知参数和可靠度的极大似然估计、Bayes估计以及E-Bayes估计.周洁等[11]在该数据类型下,基于无信息先验与伽马先验,分别考虑平方损失与Linex损失,研究了Burr XII分布的未知参数与可靠性指标的Bayes估计.李艳玲[12]在该数据类型下,研究了指数分布中两个参数的Bayes预测问题.杨君慧等[13]基于该数据类型,在两种先验信息下给出了广义指数分布中参数的Bayes估计.郭红莹等[14]在该数据类型下,分别给出Burr分布基于q-对称熵损失函数、复合Linex对称损失函数的Bayes估计以及多层Bayes估计.Wang[15]研究了该数据类型下一般截尾分布参数的区间估计问题.邓严林[16]在该数据类型下,获得了Topp-Leone分布中未知参数的极大似然估计与Bayes估计,通过后验密度分布函数讨论了参数的Bayes预测值和预测区间.刘芹等[17]同样基于该数据类型,在Linex损失函数与复合Linex损失函数下,考虑无信息先验分布与共轭先验分布,讨论Pareto分布中未知参数的Bayes估计.可见,在进行贝叶斯统计推断时常常会选取不同的先验信息,使用不同的损失函数对参数进行研究[18-19].
尽管已有一些学者对双边定数截尾样本进行了研究,但其中大部分是对其他分布的参数进行研究.基于双边定数截尾样本对服从线性指数分布的参数估计方面的研究较少,因此,本文基于双边定数截尾情形下线性指数分布的参数估计进行研究.本文主要分为三个部分:第一部分主要讨论双边定数截尾下线性指数分布中未知参数的极大似然估计(maximum likelihood estimation,MLE);第二部分讨论参数的贝叶斯估计,由于贝叶斯估计涉及复杂的积分,故采用Tierney-Kadane近似法获得参数的贝叶斯估计的近似值;第三部分通过模拟实验对所选模型的方法进行比较,并给出结论.
1 极大似然估计
若随机变量X服从线性指数分布,记为X~L(θ,μ),其分布函数为

(1)
概率密度函数为

(2)
在本文中假设μ>0为已知常数,而θ为未知参数且θ>0.
设有一批产品的失效时间服从线性指数分布,现从中随机抽取n件对其寿命进行试验,直到有r件产品失效为止,停止试验,则前r件失效产品的寿命依次为x1≤x2≤…≤xr(r≤n).在现实生活中,因为各种限制因素,包括但不限于试验条件等,可能会导致一些数据无法被观察到.假设前(s-1)个数据丢失,则剩余失效数据依次为xs≤xs+1≤…≤xr-1≤xr(1≤s≤r≤n),这类试验通常被称作双边定数截尾试验.记x*=(xs,xs+1,…,xr-1,xr),则得到似然函数为

(3)
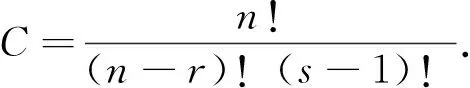

(4)
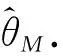
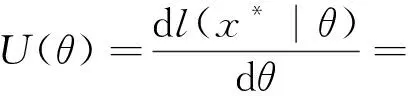
(5)
显然式(5)关于参数θ没有显式解,但可以证明方程U(θ)=0在(0,+∞)上有唯一解.设
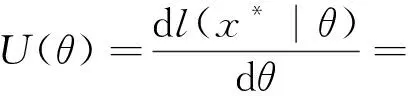
(6)
则
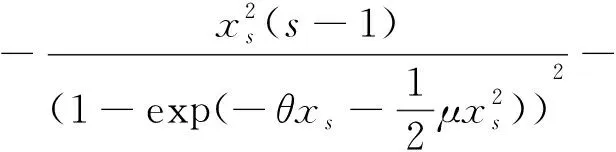
(7)
且

(8)
因此方程U(θ)=0在(0,+∞)上有唯一解.

2 参数θ的贝叶斯估计
在贝叶斯统计推断中,常常根据无信息先验分布与共轭先验分布讨论参数的Bayes估计问题,接下来本文基于这两类先验分布讨论未知参数的贝叶斯估计问题.
2.1 无信息先验下未知参数θ的Bayes估计
在进行贝叶斯统计推断时需要利用先验信息,但常常会出现一种情况:没有先验信息或者只有极少数先验信息可以利用,但仍然想用贝叶斯方法,此时需要参数空间中任何一点θ没有偏爱的先验信息[20].均匀分布和广义先验分布通常被选取为先验分布,现假定参数θ无任何先验信息,取θ的先验分布π1(θ)为(0,c)上的均匀分布,即
(9)
根据式(3)似然函数可得
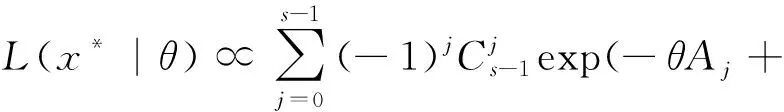
(10)
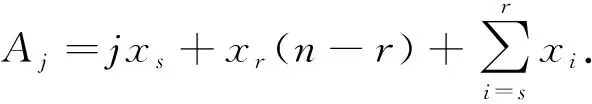
根据式(9)和式(10),θ的后验密度函数为
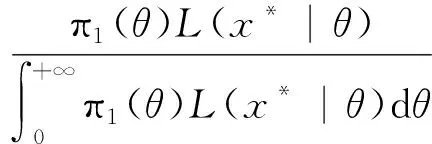
(11)
在平方损失函数下,参数θ的兴趣函数g1(θ)=θ的Bayes估计是其后验密度函数的均值,因此有
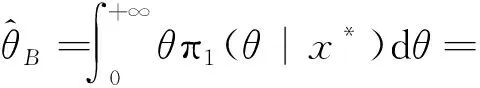
(12)
为了避免贝叶斯估计中复杂的积分计算问题,利用Tierney-Kadane近似法进行计算.令

对式(12)利用Tierney-Kadane近似可重新表示为:
(13)
(14)
在此情况下,可得到

(15)

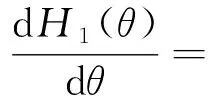
(16)
对H1(θ)关于参数θ求二阶导,有
(17)

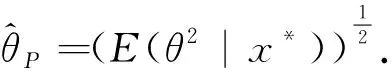
根据式(11)后验分布可得
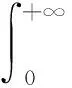
(18)
因此在预防损失函数下参数θ的Bayes估计为
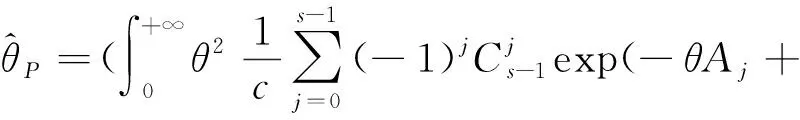
(19)
基于该先验分布在预防损失函数下的贝叶斯估计利用Tierney-Kadane近似法计算同上.
2.2 共轭先验信息下未知参数θ的Bayes估计
选取Gamma分布为线性指数分布中未知参数θ的共轭先验分布时,其概率密度函数为
(20)
其中超参数a>0、b>0.
根据式(10)和式(20),得参数θ的后验分布为
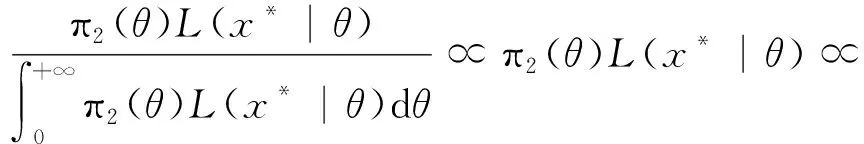
(21)
在平方损失函数下,参数θ的兴趣函数g2(θ)=θ的Bayes估计为
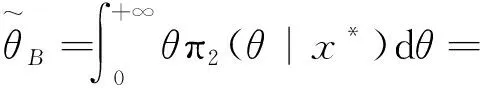
(22)
为了避免贝叶斯估计中复杂的积分计算问题,利用Tierney-Kadane近似法进行计算.令
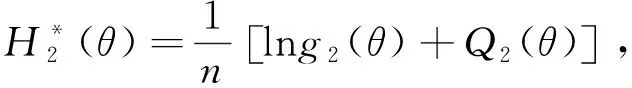
对式(22)利用Tierney-Kadane近似可重新表示为:
(23)
(24)
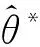
在此情况下,得到
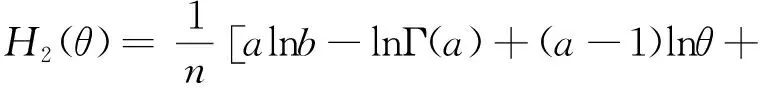
(25)

(26)
对H2(θ)关于参数θ求二阶导,有
(27)

根据式(21)可得

(28)
因此,基于伽马先验分布在预防损失函数下未知参数θ的Bayes估计为
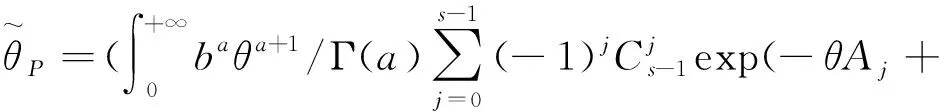
(29)
基于伽马先验信息在预防损失函数下的贝叶斯估计利用Tierney-Kadane近似法计算同上.
3 数值模拟
假设产品的寿命数据X服从LED,即X~L(θ,μ),参数θ的真实值θ=0.7,超参数a=1、b=1.5、c=1,模拟过程如下:
(1)产生n个服从U(0,1)分布的相互独立随机数u1,u2,…,un,则
即xi为来自线性指数分布的样本量为n的随机数,给定s、r的值,得到双边定数截尾试验样本
x*=(xs,xs+1,…,xr-1,xr);
(2)取μ=1时,基于双边定数截尾样本计算参数θ的极大似然估计和贝叶斯估计;
(3)对(1)、(2)步骤重复2 000次,得到参数θ的极大似然估计和贝叶斯估计的均方误差(mean square error,MSE);
(4)对n、s、r取不同的值得到不同的样本量、不同的截尾方式,重复以上步骤,得到模拟结果如表1所示.

表1 参数θ的各种估计的均方误差
表1给出了当μ=1时不同的截尾方案下参数θ的MLE与Bayes估计的MSE,从表1可以看出:
(1)增加样本量时,除了截尾方案(n,s,r)为(50,4,47)时伽马先验下平方损失函数的贝叶斯估计均方误差和(n,s,r)为(40,3,38)时伽马先验下预防损失函数的贝叶斯估计均方误差不是逐渐降低外,两种参数估计的均方误差逐渐降低;
(2)在同一样本量下,随着丢失个数s的减小、失效个数r的增大,极大似然估计的均方误差与贝叶斯估计的均方误差均在减小;
(3)取无信息先验为均匀分布时,极大似然估计方法得到的未知参数的均方误差比平方损失函数与预防损失函数的Bayes估计的均方误差更小;
(4)取无信息先验为均匀分布时,平方损失函数下贝叶斯估计的均方误差均小于预防损失函数下贝叶斯估计的均方误差;
(5)取先验分布为伽马分布时,极大似然估计的均方误差均大于贝叶斯估计的均方误差;
(6)取先验分布为伽马分布时,平方损失函数下贝叶斯估计的均方误差较预防损失函数下贝叶斯估计的均方误差更小,因此平方损失函数下参数的贝叶斯估计的均方误差总体上最小.
综上,伽马先验下贝叶斯估计的均方误差效果优于极大似然估计的均方误差效果,极大似然估计的均方误差效果优于无信息先验下贝叶斯估计的均方误差效果,且选取Gamma先验分布并在平方损失函数下,未知参数的Bayes估计均方误差效果最优.
例1若取μ=1、θ=0.7,产生样本量为40且服从线性指数分布的简单随机样本如下:
0.000 16,0.025 89,0.038 61,0.054 77,0.117 17,0.126 90,0.134 90,0.190 25,0.198 57,0.228 57,0.249 86,0.265 17,0.273 37,0.400 01,0.414 49,0.417 22,0.456 70,0.525 11,0.552 68,0.553 07,0.555 66,0.558 28,0.719 00,0.727 56,0.758 09,0.946 26,0.973 85,0.976 28,0.986 57,0.987 43,1.043 06,1.106 58,1.227 78,1.322 15,1.461 30,1.467 81,1.467 90,1.533 86,1.912 45,2.018 54.
现对丢失个数和失效个数取不同的值,得到不同的双边定数截尾样本,使用本文的估计方法对参数进行估计,计算结果如表2所示.

表2 样本量为40不同截尾方案下参数θ的各估计的均方误差
从表2可以看出:在同一样本量下,随着丢失个数s的减小、失效个数r的增大,极大似然估计的均方误差与贝叶斯估计(a=1、b=2.5、c=1)的均方误差均在减小;Gamma先验下取平方损失函数时线性指数分布参数的贝叶斯估计更准确.
4 结论
在统计分析中,极大似然估计方法与贝叶斯估计方法是常见的两种估计方法,本文分别运用这两种方法对线性指数分布的未知参数进行估计.基于双边定数截尾试验,首先用极大似然估计法估计线性指数分布的参数;其次选取无信息先验和Gamma先验分别在平方损失函数和预防损失函数下对线性指数分布的未知参数进行Bayes估计.为避免贝叶斯估计中复杂的积分计算问题,提高参数估计的精度,利用Tierney-Kadane近似法获得了双边定数截尾下线性指数分布的近似贝叶斯估计.数值模拟表明:样本量增加时参数估计的均方误差逐渐减小,估计具有大样本性质;Gamma先验下取平方损失函数时线性指数分布参数的贝叶斯估计的均方误差总体上是最小的.
