基于加权潮流熵和耦合支路介数的大停电故障集构建方法研究

郭 裕，刘石川，高雯曼，李丹丹，张爱军，姜希伟

（1.内蒙古电力（集团）有限责任公司内蒙古电力科学研究院分公司，呼和浩特 010020；2.中国电力科学研究院有限公司，北京 100192；3.内蒙古电力（集团）有限责任公司电力调度控制分公司，呼和浩特 010020）

近年来，国内外电网连锁故障时有发生，每次故障均会造成重大的经济损失和社会影响。例如：“8.14”美加大停电，“8.28”英国伦敦大停电，“9.23”丹麦瑞典大停电，“7.12”希腊大停电，“7.30”、“7.31”印度大停电，英国“8.9”大停电事故，停电范围和损失负荷大，严重影响了正常的生产生活[1]。

我国电网也发生了数次较大规模停电事故。2006 年7 月1 日河南电网500 kV 嵩郑两回线路突然发生故障先后跳闸引起大规模潮流转移，造成豫西、豫中部分220 kV 线路连锁过载跳闸，导致大面积停电事故；2008年1月，因冰雪灾害，贵州、湖南、湖北、江西等省发生大面积停电[2]。2022 年3 月3日，中国台湾电网发生大面积停电事故，损失负荷约8.46 GW[3]。

电网正常运行时线路传输一定的有功功率，当其中某条或某几条线路退出运行后，停运线路上的潮流就会转移到其他支路上，如果其他正常运行的支路不能承担这部分转移潮流，就会因过载而停运，导致连锁故障发生[4]。连锁故障在电网中出现的几率很小，但是一旦发生，影响就会非常严重。因此，充分了解连锁故障机理，构建连锁故障导致电网大停电的故障集对于保障电力系统安全稳定运行具有重要意义[5-6]。

目前，大停电故障集构建技术主要分为两大类：一类是基于时域仿真分析，其优点可以通过将电网元件精细化模拟达到较高的仿真精度，但其依赖人工经验设定大量故障，通过大量仿真分析并依托人工经验确定大停电故障集，难以保证故障集的覆盖范围，也可通过风险等级指标进一步完善故障集的构建。另一类是基于复杂理论的分析，可以从整体上把握电网发生大停电事故的风险，依托幂律规律反映电网大停电事故频度和损失的关系，目前通过引入电气距离等因素逐步将其从信息理论研究转向电力系统应用的研究[7-8]。文献[9]提出考虑连锁故障传播特性的电网脆弱线路辨识方法，但其实际应用复杂；文献[10]分析传统交流电网与高比例新能源的连锁故障差异性，指出新能源的强随机性、不确定性、低抗扰动能力等特性在一定程度上弱化了电网原有强度；文献[11]提出基于模糊熵权法的元件综合风险责任量化方法辨识输电系统的薄弱环节；文献[12]提出基于微型PMU 的预想故障集组合筛选方法，然而，这一方法主要采用电网拓扑结构的直接分析法或采用静态潮流分析等方法进行连锁故障序列判断，未能考虑元件动态特性特及在电网故障振荡过程中元件的动态响应特性。实际在大停电过程中，每一阶段故障后电网动态元件的运行状态均会发生变化，因此仅依靠上述方法来全面掌握大停电事故构建技术存在较大的缺陷[13-14]。

综上，本文拟提出一种基于潮流熵、耦合支路介数等复杂系统理论和全过程动态仿真技术的大停电故障集构建方法。其具有以下几个特点：

（1）采用耦合支路介数量化评估电网结构变化引起的大规模停电事故风险，采用加权潮流熵量化评估电网状态变化引起的大规模停电事故风险；

（2）兼顾电网结构变化和电网状态变化，提出基于潮流熵、耦合支路介数等复杂系统理论的大停电故障集构建方法，能够准确反应电网故障动态过程。

（3）兼顾各种元件中长期动态过程的精细化模拟，利用全过程动态仿真技术校核故障集选取是否有效，高效率选择故障集。

1 耦合支路介数

耦合支路介数作为线路脆弱性的评价指标，以电网的拓扑结构为基础，是结合支路电抗参数建立的加权拓扑模型。在分析过程中，耦合支路介数不仅考虑当前运行方式下的各支路的潮流权重，同时还考虑待评价支路的最大相关性支路的影响[15-16]。

基于耦合支路介数的电网关键支路识别方法，包括形成基础矩阵、关键支路子集选取和耦合支路介数计算

1.1 形成基础矩阵

针对电力系统典型运行方式数据，分别建立以支路电抗值为权重的边权连接矩阵B和包含支路功率大小、方向、负载率的支路潮流权重矩阵W，以及节点-支路关联向量Mij和节点电抗矩阵X。

边权连接矩阵B可表示为

式中：xij为支路Lij的线路电抗值，i,j∈n，n为电网节点总数；Bij为边权连接矩阵B第i行，第j列的变量，表示节点i和节点j的连接阻抗。

支路潮流权重矩阵W可表示为

式中：Pij为支路Lij的有功功率；Pmax为支路Lij的传输稳定限额；Wij为支路潮流权重矩阵W第i行第j列的变量，表示支路Lij潮流权重。

一旦节点i和节点j之间有线路，则节点-支路关联向量Mij可表示为

式中：i节点矩阵元素为1；j节点矩阵元素为-1。

节点电抗矩阵X可表示为

式中：Xii为节点i的自阻抗；Xij为节点i、j间的互阻抗。

支路包括输电线路和变压器。将并列的线路或变压器合并为单一元件，并以其合并后等值电抗值为权重，形成边权连接矩阵，不计支路电阻和对地电容支路的影响。

1.2 关键支路子集选取

以第1.1 节生成的边权连接矩阵B为对象，断开任一支路Lpq，若支路Lpq断开后电网解列为两部分，则支路Lpq列入关键支路子集1；若支路Lpq断开后电网仍为一个整体，则支路Lpq列入备选集1。

按照如下规则对全部支路进行扫描：①断开任一支路Lpq，对应的边权连接矩阵中的元素Bpq=Bqp=∞；②对改变后的边权连接矩阵，从节点1开始，查找与节点1 直接相连的节点，进而查找与这些节点相连的其他节点，直至遍历全部节点。若节点1 不能遍历全部其他节点，则支路Lpq断开后电网解列为两部分；若节点1可以遍历全部其他节点，则支路Lpq断开后电网仍为一个整体。

1.3 耦合支路介数Sij 计算

从节点i开始遍历所有可能到达节点j的路径，计算得到最短路径Z，其等值阻抗为

式中：k为所有可能达到路径中介于i、j之间的节点，最短路径一般由多条支路串联构成；Bik为节点i和节点k的连接阻抗，其定义见式（2）。

在最短路径Z上寻找与由节点i到节点j方向相同，且初始潮流权重（依据第1.1节生成的支路潮流权重矩阵W）最大的支路Lrs，并计算支路Lrs在支路Lij断开后的潮流转移因子Drs_ij。

式中：xij、xrs分别为支路Lij、Lrs的线路电抗值；Zrs_ij=，Mij、Mrs分别为支路Lij、Lrs的节点-支路关联向量。

计算支路Lij的耦合支路介数Sij为

式中：Sij为耦合支路介数指标；Drs_ij为支路Lij断开后转移至支路Lrs的潮流转移因子；Wij、Wrs分别为支路Lij和Lrs的支路潮流权重，其定义见式（4）。

所提耦合支路介数Sij不仅考虑当前运行方式下的各支路潮流权重，还考虑待评价支路Lij的最大相关性支路的影响；Drs_ij值越大，支路Lrs传输有功功率越限的风险越大；同时考虑支路Lrs的运行状况，支路Lrs的潮流权重Wrs越大，受支路Lij影响发生故障的风险越大，对下一级故障的影响也越大。耦合支路介数是一个综合评估指标，既考虑了有功功率的绝对大小，还考虑了功率裕度的相对值，并且结合了前后两级故障，所得结果更加符合电网实际情况。

2 加权潮流熵计算方法

熵理论反映了一种自然界现象有序程度的演化规律，广泛应用于评估系统中关键指标的有序和稳定程度，在信息科学、生命科学、系统科学、管理科学、行为科学等众多领域得到广泛应用。对于一个广义的复杂系统来说，熵可作为分布状态的混乱性和无序性的量度[17]。

电力系统潮流分布是电网运行状态的重要标志，合理的潮流分布和电压水平下的电网安全稳定水平较高、抗故障冲击能力较强；不合理的无序的潮流分布情况下电网安全稳定水平较差，易发生失稳事故。因此，采用熵指标评估电网典型运行方式的潮流分布有序性，分析复杂电网自组织临界状态演化规律，评估电网发生大规模停电事故风险，是近年来的研究热点。

首先建立潮流分布熵的概念。设线路i的传输稳定限额为Pmax，电网运行时线路i实时传输功率为Pi0，则线路i的负载率μi0为

综合考虑电网正常运行情况和可能遇到的故障后极端情况，并考虑一定的裕度，设可能的线路负载率区间为[0，2.0]，即线路可能空载，也可能达到负载率2.0的极端状况。

按照一定的步长τ将负载率区间进行细分，形成负载率细分区间序列为{[0,τ],(τ,2τ],…,((k-1)τ,kτ],…,((m-1)τ,2.0]}，其中，m=2/τ，k=1,2,…，m。例如，取τ=5%，即可形成负载率区间的不同细分段，[0，0.05]，（0.05，0.10]，（0.10，0.15]，…，（1.90，1.95]，（1.95，2.00]。

设λk为负载率μk0∈((k-1)τ,kτ]的线路条数，则得到负载率在该区间段的线路占全网线路的概率，即

则潮流熵可表示为

式中：C1为常数，可根据研究需要设定；m为状态数。

研究表明，潮流熵即潮流分布不均衡性对电网连锁故障传播具有重要影响，是决定电网是否进入自组织临界态的重要因素，较好地解释了实际电网在平均负载率较低情况下由于线路潮流分布高度不均衡性而进入自组织临界态的现象。但是，潮流熵只考虑了线路负载率在各区间的分布情况，未考虑各区间负载率差异对电网状态的影响，可能导致分析结果与电网实际不符。因此，提出加权潮流熵，即

式中，ζk为((k-1)τ,Kτ]区间线路的平均负载率。ζk可表示为

3 大停电故障集构建方法

加权潮流熵和耦合支路介数等复杂系统理论主要采用静态潮流分析等方法进行连锁故障序列判断，未能考虑元件动态特性特别是在电网故障振荡过程中元件的动态响应特性。实际上在大停电过程中，每一阶段故障后电网动态元件的运行状态均会发生变化，因此仅依靠第2节的方法来全面掌握大停电事故构建技术存在较大的缺陷。

全过程动态仿真技术可以实现对各种元件中长期动态过程的精细化模拟，是对大停电仿真计算的有力工具。在大停电长时间过程中，当电网由警戒状态经故障冲击或强连锁故障冲击下进入紧急状态时，全过程动态仿真程序可以实现较好的各种元件自动动作进而诱发大停电过程模拟[18]；但在大停电发展初期，当电网由正常状态向警戒状态过渡时，可能诱发该过程的故障形式和组合千变万化，采用全过程动态仿真程序对每一种可能的故障形式进行研究既不现实也无必要。

因此，本文提出一种基于加权潮流熵和耦合支路介数等复杂系统理论筛选可能的连锁故障形式，再由全过程动态仿真程序判断是否会发生电网崩溃事故。具体方法如图1所示，其步骤如下。

图1 所提故障集构建方法流程Fig.1 Flow chart of the proposed construction method for fault set

步骤1建立电力系统典型运行方式数据。

步骤2由式（13）计算该方式下电网的加权潮流熵。若加权潮流熵超过门槛值，则转步骤6；若加权潮流熵未超过门槛值，则转步骤3。加权潮流熵门槛值为0.5。

步骤3判断线路潮流是否越限。若线路潮流越限，转步骤6；若线路潮流未越限，转步骤4。

步骤4基于耦合支路介数指标计算当前电网中的关键支路，形成关键支路集。

步骤5计算关键支路集中任一支路断开后的潮流。若潮流收敛，则转步骤2；若潮流不收敛，则转步骤6。

步骤6整理连锁故障序列，形成连锁故障集，为全过程动态仿真提供运行方式，并为连锁故障设置信息。

步骤7启动全过程动态仿真程序，按照步骤6形成的连锁故障集逐一进行计算。若发生连锁故障，导致电网失稳，计算结束；若未发生连锁故障导致电网失稳，转步骤3。

4 案例分析

以某地区实际电网为例进行案例分析，其电网结构示意如图2 所示。由图2 可以看出，该地区电网通过LHS1、LHS2、LHS33 条500 kV 双回线路同电网S相联；通过LHB1、LHB22条500 kV双回线路同电网B 相联；通过LHT11 条500 kV 双回线同电网T 相联；通过LHD1、LHD22条500 kV双回线路同电网D相联。LM为连接站M和站F的线路。仅针对500 kV线路，各线路额定功率取1 980 MW，对应额定电流2 300 A。

图2 某地区网架结构示意Fig.2 Schematic of structure of one regional grid

针对某省丰大典型方式，计算系统加权潮流熵为0.427，未超过门槛值0.500。

基于耦合支路介数指标计算当前电网中的关键支路，形成关键支路集，其结果如表1 所示。由表1 可知，LHS3双回线的耦合支路介数最大，故断开LHS3双回线后计算潮流，潮流不收敛，选择LHS3双回线N-2 作为连锁故障的首故障。使用全过程软件仿真LHS3的N-2故障，电网未崩溃，但LM双回线稳态恢复潮流越限，将其作为下级连锁故障。

表1 关键支路耦合支路介数Tab.1 Coupling branch intermediate index of critical branches

启动全过程动态仿真程序，仿真故障序列为LHS3、LM，故障间隔时间1 min，仿真结果如图3 和图4所示。

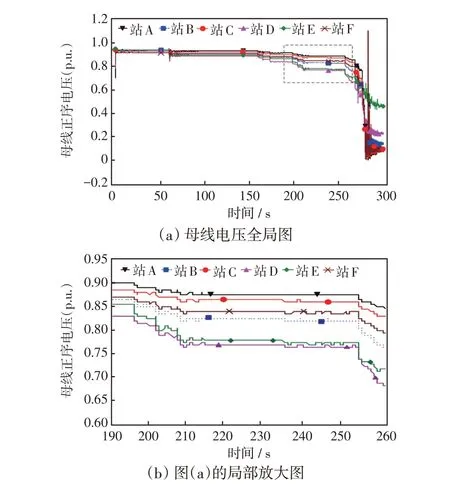
图3 部分母线电压变化情况Fig.3 Changes in voltage of some buses

图4 机组功角变化情况Fig.4 Changes in power angle of generators

由图3 可以得出，整个连锁故障过程中节点电压是动态的，由于发电机组励磁的作用，使得在LHS3首故障后部分电压波动并不明显；60 s 后发生LM双回线跳开，后续故障从159.4 s开始，由于发电机保护动作导致发电机陆续跳机，母线电压跌落，继而发生电网崩溃。由图4可以得出，在270 s附近发生机组功角失稳现象。

图5 为整个连锁故障动态过程中系统加权潮流熵的变化情况。由图5 可以看出，①故障发生前，初始潮流下系统加权潮流熵为0.427，即图中的A 点，未超过门槛值；主力发电机励磁电流为0.81～0.99 p.u.，未超过门槛值，因此电网发生大停电事故的风险不大，但熵值已靠近边界，仍存在一定的停电事故风险。②通过对该区域电网全网各支路耦合支路介数计算，选定对电网影响最大的LHS3双回线故障为首故障。LHS3双回线故障后，电网保持稳定，系统加权潮流熵增大至0.590，即图中的b点，超过门槛值，电网发生大停电事故的风险大大增加。发生该故障后，大量潮流在由北向南涌动，潮流主要转移至LM双回线，导致其潮流越限。③选择LM双回线故障作为后续故障，即图中的c点、d点。该故障发生后，潮流进一步转移至LED线路，潮流转移沿线母线电压大幅跌落，机组转子过负荷保护相继动作，即图中的e点、f点，进一步降低了无功电压支撑能力，最终导致电压崩溃。④电网振荡过程中，由于低压解列装置动作，即图中的g点，LHD2双回线断开，导致整个地区电网仅通过LED同主网相联，形成长链状电网结构，引发功角失稳，即图中h点。

图5 连锁故障动态过程中系统加权潮流熵变化情况Fig.5 Changes in weighted power flow entropy of system during the dynamic process of cascading faults

由表1中数据可得LHD2双回线的耦合支路介数由大到小排列位居第2，断开LHD2双回线后，潮流收敛，潮流熵为0.460，小于门槛值0.500。

通过排查500 kV 线路（非500 kV 直连电厂出线）功率及负载率，可以得到LHD1双回线过载，作为后续故障。

启动全过程动态仿真程序，仿真故障序列LHD2、LHD1，故障间隔时间为1 min。故障后，省间联络线只剩LHD1双回线，区域联络线还有特高压双回线，大规模潮流转移，使LHD1双回线潮流过载。LHD1双回线潮流过载跳开后，相邻电网同该地区电网发生功角失稳，相对功角变化情况如图6所示。

图6 该地区机组同相邻电网机组相对功角变化曲线Fig.6 Curve of relative power angles between generators in the regional grid and those in neighboring grid

4 结 语

本文首先考虑电网拓扑结构变化，研究基于耦合支路介数的电网关键支路识别方法；其次，考虑电网状态变化提出加权潮流熵计算方法，定量评估电网的运行状态；然后，结合全过程动态仿真软件，提出基于加权潮流熵和耦合支路介数的大停电故障集构建方法；最后，以某地区电网实际数据为例验证了所提故障集构建方法的有效性和准确性。

所提方法既考虑电网结构变化和电网状态变化，能够准确反映电网故障动态过程，又利用全过程动态仿真工具对生成的故障集进行校核，防止大停电连锁故障发生。