基于负荷预测和无迹粒子滤波的配电网动态状态估计
2024-05-07卢锦玲胡兴华张学哲王恩泽赵增辉
卢锦玲,胡兴华,张学哲,王恩泽,赵增辉
(华北电力大学电气与电子工程学院,保定 071003)
在全球化石能源短缺、环境污染严重的背景下,发展清洁、可再生能源已经成为发展趋势。多国实施免征购置税、财政补贴、建设充电设施等政策,促进了电动汽车的发展,电动汽车充电需求逐渐成为配电网应重点考虑的新型负荷[1]。但大量电动汽车的接入可能会导致配电网日负荷曲线的峰值提高、节点电压下降等问题,对配电网造成较大的冲击[2]。要保障配电网的安全可靠运行,需要对电动汽车负荷进行实时、准确的态势感知。状态估计作为配电网态势感知技术的基础,为其提供了有效的数据支撑,对配电网的运行与控制安全起着重要作用。
状态估计也被称为滤波,电力系统的状态估计分为静态状态估计和动态状态估计。静态状态估计主要是利用最小二乘法等方法进行迭代,通过优化量测数据与系统模型间的残差来获得最佳的状态估计结果,算法较为简单,稳定性好。但随着风电、光伏等分布式电源和电动汽车等柔性负荷的增多,配电网不确定性因素增加,要对系统未来运行趋势进行预测,采用动态状态估计更为合适。动态状态估计可以体现电力系统中节点的电压、相角状态随时间变化的过程,在保证状态估计结果准确性的同时无需迭代,减少了计算量,时效性更强,且计算结果包含预测信息[3]。最初的动态状态估计以扩展卡尔曼滤波EKF(extended Kalman filter)为基础,但由于需要计算雅可比矩阵导致算法复杂度较高,同时线性化近似也会导致估计不准确的问题[4]。Julier等[5]和卫志农等[6]提出了无迹卡尔曼滤波UKF(unscented kalman filter),利用无迹变换方法,即通过一组Sigma点进行采样来近似非线性系统的状态分布。文献[7]利用Holt’s 两参数指数平滑法描述电力系统的动态模型,并对UKF 算法进行改进,通过引入噪声统计估值器来估计系统噪声的均值和方差。文献[8]利用云自适应粒子群算法优化脉冲神经网络预测生成伪量测模型,并与改进的UKF算法结合进行虚假数据注入攻击FDIA(false data injection attack)辨识。文献[9]先用相似日法和极端梯度提升进行日前负荷预测,再通过与UKF算法结合进行FDIA 辨识。文献[10]利用改进粒子滤波算法对综合能源系统进行状态估计,解决了跟踪误差问题。然而,使用UKF算法进行滤波时精度受参数影响变化较大,灵活性较差,同时初值选取不准确也可能导致难以收敛的情况。而粒子滤波虽然能通过改变粒子数影响估计结果,但在生成重要性密度函数时不能充分利用量测信息,滤波效果有待提升。为此,本文使用无迹粒子滤波UPF(unscented particle filter)算法进行初步动态状态估计,可以克服前述方法的局限性,提供更好的滤波效果。
由于配电网的规模较大且结构复杂,量测配置冗余度较低,再加上测量噪声和不良数据的影响,可能导致状态估计的准确性下降,无法对系统的状态进行全面监测。为此,可以利用负荷预测辅助状态估计结果,弥补有效量测数据不足等问题。目前,国内外进行短期负荷预测的方法主要分为统计方法和时间序列方法、机器学习方法及深度学习方法。统计方法和时间序列方法主要包括移动平均法、指数平滑法、回归分析法和自回归移动平均模型等。机器学习方法和深度学习方法主要包括支持向量机、决策树、随机森林和卷积神经网络CNN(convolutional neural network)、循环神经网络RNN(recurrent neural network)等[11]。LSTM(long shortterm memory)与GRU(gated recurrent unit)都是RNN的变体,区别在于门控的不同[12-13]。文献[14]提出了一种基于卷积神经网络-生成对抗网络CNN-GAN(convolutional neural network-generative adversarial network)与半监督回归的电动汽车充电负荷预测方法,同时考虑了天气因素与历史负荷数据,利用半监督回归进行输出。文献[15]利用CNN-LSTM模型对综合能源系统进行负荷预测,同时考虑了电、冷、热负荷间的耦合关系。研究发现,通过结合不同神经网络的优点,使用组合预测模型比单一神经网络模型的预测准确度会有不小的提升。
基于此,本文以加入了电动汽车充电的居民区日用电为基础,提出一种基于CNN-GRU 模型负荷预测和UPF 算法混合的配电网动态状态估计方法。首先利用CNN-GRU 进行短期负荷预测,根据网络拓扑信息对预测结果进行潮流计算;然后,将潮流计算结果与UPF 算法初步状态估计的结果自适应加权混合得到最终状态估计结果;最后,在IEEE33 节点配电系统中进行仿真实验,实验结果表明,所提配电网动态状态估计方法不仅拥有较高的准确度,同时在量测中含有不良数据时也具有较好的鲁棒性。
1 基于CNN-GRU 的短期负荷预测
根据拥有电动汽车的居民区历史有功功率和无功功率数据,使用CNN-GRU 神经网络模型对居民区进行短期负荷预测。
1.1 CNN 模型
CNN 可以实现区域连接与参数共享。在输入原始数据后,其能够自动捕捉更加复杂和抽象的数据特征。CNN 通常包括卷积层、池化层与全连接层,分别起到特征提取、压缩降维、整合处理的作用。此外,在卷积层后一般要加上激活函数,常用的激活函数是ReLU,用来给模型提供非线性映射的能力,提升其在处理复杂数据特征时的性能。
1.2 GRU 模型
GRU 与LSTM 都属于RNN,适用于分析时间序列数据。相比于LSTM,GRU由输入、遗忘和输出3个门控减少为两个门控,分别为更新门和重置门[13]。GRU 可以在更少的结构参数与更短的训练时间下达到期望的准确度。GRU 结构如图1 所示。GRU的更新公式为
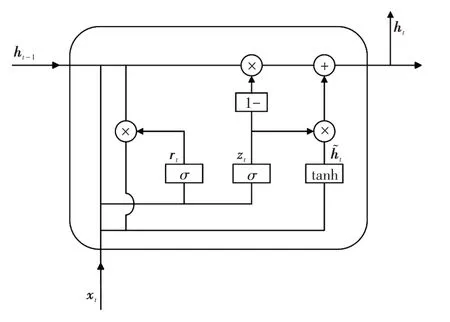
图1 GRU 结构Fig.1 Structure for GRU
式中:xt为输入向量;σ( )为sigmoid激活函数;tanh( )为双曲正切激活函数;[,]表示向量连接;rt为重置门;zt为更新门;为候选隐藏状态;ht为最终隐藏状态;ht-1是上一时刻的隐藏状态;Wr、Wz和W为权重参数矩阵;br、bz和bh为偏置参数向量。
1.3 CNN-GRU 组合预测模型
CNN-GRU组合预测模型首先通过CNN对输入数据进行特征提取,再将特征序列传递给GRU,从而获取序列数据中的时间相关性且不会丢失关键历史信息,以此进行负荷预测。CNN-GRU 组合预测模型的流程如图2所示。
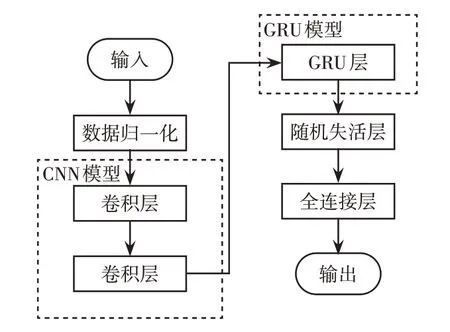
图2 CNN-GRU 组合预测流程Fig.2 CNN-GRU combined prediction process
图2中CNN-GRU组合预测流程具体步骤如下。
步骤1将有效历史数据集进行归一化处理。
步骤2将归一化后的数据输入到CNN 中提取特征,CNN 共包含2 层一维卷积层,每层卷积层都有64个大小为3×3的卷积核,不包含池化层。
步骤3数据通过CNN 提取特征后再输入到GRU 中,进行时间序列预测,GRU 中包含256 个隐藏单元。
步骤4为了防止模型过拟合,添加随机失活层来随机丢弃一部分神经元的输出,丢弃率为0.3。
步骤5通过全连接层输出有功功率与无功功率的预测结果。
2 基于UPF 的配电网动态状态估计
2.1 UPF 算法原理
传统粒子滤波通常直接采用先验概率密度作为重要性密度,没有考虑量测信息,在进行后验估计时误差较大,用于电网状态估计时滤波效果很差[16]。而UPF 算法是在传统粒子滤波的基础上将重要性密度函数用UKF生成,相比于UKF和传统粒子滤波,使用UPF算法进行电网状态估计时精度有很大提升。
2.2 UPF 算法步骤
步骤1初始化。当时刻k=0 时,设初始的状态变量为x0,通过概率密度p(x0) 生成{,i=1,2,…,N}粒子集,其中N为粒子个数,每个粒子的初始权重=1/N。
步骤2当时刻k>0 时,利用UKF算法对每个粒子生成重要性密度函数,采样得到新粒子。
步骤3使用对称采样法进行无迹变换,对每个粒子构造Sigma点集{} 和其对应的权值,即
式中:n为状态变量维数;2n+1 为Sigma 点的个数;和分别为每个粒子在k-1时刻的UKF估计值和状态变量协方差矩阵;λ为尺度因子,用于降低预测误差,λ=α2(n+κ)-n;α为比例修正因子,取值范围通常为[1×10-4,1];κ为自由参数,用来保证(n+λ)矩阵半正定;[ ]j表示矩阵的第j列;Wj,m和Wj,c分别为Sigma点的均值权值和方差权值;β为参数,在高斯分布情况下一般β取2。
步骤4根据状态转移函数f( )对粒子采样得到的Sigma点集进行预测进而得到点集{} ,即
式中:qk-1为状态转移过程噪声;状态转移函数f( )采用Holt’s两参数法[7],具体公式为
式中:为水平值;为趋势值;αH为水平平滑系数;βH为趋势平滑系数,取值范围为[0,1]。
根据预测点集{} 得到状态变量的一步预测均值和协方差矩阵,即
式中,Qk-1为过程噪声协方差矩阵。
步骤5对粒子根据和按照步骤3再次构造新的Sigma 点集,然后再根据量测函数得到量测预测点集和均值,即
式中:rk为量测噪声;h( )为量测函数,由网络拓扑决定。
步骤6得到粒子的自协方差矩阵和互协方差矩阵,即
式中,Rk为量测噪声协方差矩阵。
步骤7对粒子计算卡尔曼增益,更新粒子状态变量估计值和协方差矩阵,即
式中,zk为实际量测值。
步骤8生成一阶马尔可夫假设下的重要性密度函数,根据其采样得到粒子,即
步骤9更新权重并对权重进行归一化,归一化公式为
式中:为更新后的权重值;为对权重进行归一化后的值。
步骤10为避免粒子退化,判断是否重采样。根据权重计算有效样本数量,若满足(Nt=3N),则利用随机重采样法对粒子进行重采样,并将粒子权重都设为1N。
步骤11输出状态估计结果,即
式中,为利用UPF算法得到的状态估计值。
3 自适应混合动态状态估计
配电网由于系统规模和经济成本的原因,实量测配置较少,再加上测量噪声和不良数据的干扰,有效量测不足会影响到状态估计的准确性。而负荷预测在能源管理和配电网运营领域受到广泛应用,通过引入大量的历史数据,可以为配电网的状态估计提供更多信息,从而提高估计结果的准确性和全面性。为此,本文使用一种自适应混合加权的动态状态估计方法,即将根据CNN-GRU 短期负荷预测进行潮流计算的结果和UPF 的初步状态估计结果进行自适应加权融合,得到最终的状态估计结果。自适应加权法可以根据上一时刻估计结果与真实值的误差对本时刻权重进行自动更新[9]。混合状态估计模型为
式中:为混合状态估计值;为CNN-GRU负荷预测进行潮流计算得到电压、相角状态量;ωk为k时刻的权重。
权重的更新公式为
式中:为k-1时刻的最优权重,即混合状态估计值与真实值误差最小时的权重取值;αk为遗忘因子,αk越大表示对k-1 时刻的权重ωk-1遗忘越多,对k-1时刻的最优权重保留越多。
估计值与真实值的误差的计算公式[17]为
式中:xk-1为k-1 时刻的电压、相角状态量的真实值;ek-1为k-1 时刻采用最优权重时混合状态估计值与真实值的误差。
式(22)利用遗传算法求解,种群中共设置有100个个体,每个个体有2个染色体,分别代表电压幅值最优权重和相角最优权重。为综合保证混合状态估计结果的准确性与实时性,种群经过选择、交叉、变异后迭代50 代即得到最优权重结果。
遗忘因子αk的计算公式为
式中,γ为调整系数,用来决定遗忘因子的变化幅度。当k-1 时刻的误差ek-1比k-2 时刻的误差ek-2小时,应适当减小遗忘因子,即在k时刻混合状态估计时,更多保留k-1 时刻的权重ωk-1;反之应增大遗忘因子,在进行k时刻混合状态估计时,增大k-1 时刻最优权重的比例。假设不论αk如何变化,取值均在[0,1]之间,αk=0表示对ωk-1完全保留,αk=1 表示对ωk-1完全遗忘。为保证估计准确度,考虑遗忘因子变化的灵活性,将αk初值设为0.5,γ取值为0.2。
自适应混合动态状态估计流程如图3所示。
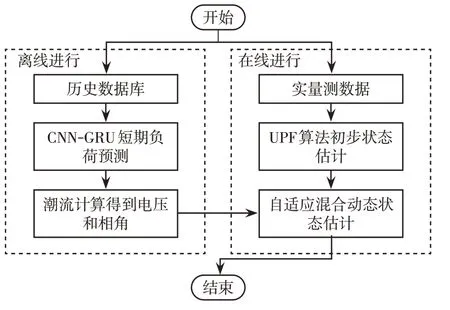
图3 自适应混合动态状态估计流程Fig.3 Adaptive hybrid dynamic state estimation process
CNN-GRU短期负荷预测部分与UPF初步状态估计部分独立运行,且由于短期负荷预测部分利用的是历史数据,因此可在离线状态下进行,不受实时性要求的限制。在进行UPF初步状态估计后,对两部分计算结果进行权重分配。所提混合动态状态估计方法在保证实时性的同时,综合考虑了短期负荷预测结果与UPF初步状态估计结果的准确度,能够得到更好的估计结果。
4 算例分析
本文选用IEEE33 节点配电系统进行仿真测试,结构如图4所示。数据集采用欧洲某10户住户居民区2016年12月—2020年1月购买电动汽车后的电力负荷数据,经过对缺失值的处理后有效数据共105 792 条。每天从00:00 开始每隔15 min 采集一次数据,一天共采集96次。
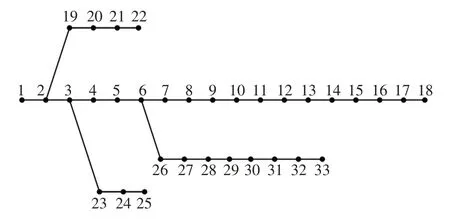
图4 IEEE33 节点配电系统Fig.4 IEEE33-bus power distribution system
4.1 实验环境配置
本文实验环境使用Intel i7-12700H 处理器,Nvidia RTX 3070Ti Laptop 显卡。仿真软件为Matlab R2022a,其中网络参数与潮流计算结果使用Matpower7.1程序得到。
4.2 实验评价指标
为了评估负荷预测与状态估计结果的精度,本文使用平均绝对百分比误差MAPE(mean absolute percentage error)、均方根误差RMSE(root mean square error)和决定系数R2(R-squared)作为评价标准,其计算公式分别为
式中:M为待评价样本总数;为第ρ个负荷预测值或状态变量估计值;yρ为第ρ个负荷真实值或状态变量真实值;为待评价样本的平均值。
4.3 基于CNN-GRU 的短期负荷预测仿真分析
以预测2020 年1 月11 日负荷的有功功率与无功功率为例。为便于神经网络模型训练,首先用ZScore标准化法对负荷数据进行归一化,即
式中:X为负荷数据原始值;Xmean为负荷数据原始值的平均值;σ为负荷数据原始值的标准差;Xnorm为归一化后的值。
初始学习率设为0.005,共训练200 轮,在第100 轮时将学习率下降到原来的0.2 倍,使用Adam优化器。有功和无功功率预测结果如图5和图6所示。使用不同预测模型的预测精度对比如表1所示。

表1 预测精度对比结果Tab.1 Comparison results of prediction accuracy
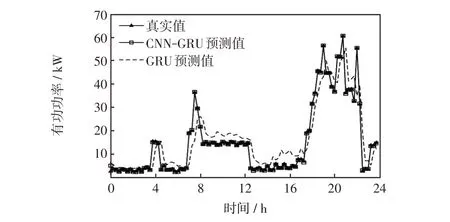
图5 有功功率预测结果Fig.5 Active power prediction results
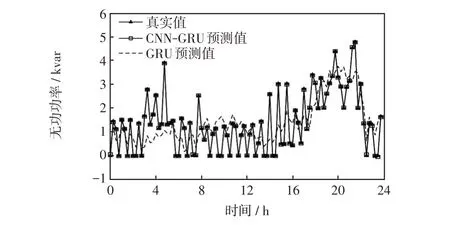
图6 无功功率预测结果Fig.6 Reactive power prediction results
从图5和图6可以看出,与GRU模型相比,CNNGRU模型预测曲线拟合良好,更加接近实际结果,由于用户下班后给电动汽车充电,晚上的用电量明显大幅超过白天,功率的峰值也较高。由表1可知,CNNGRU 预测精度较高,具有明显优势,由于无功功率的真实值中存在0 kvar,故其MAPE不进行计算。
4.4 动态状态估计仿真分析
4.4.1 UPF 算法不同粒子数测试
取IEEE33节点配电系统中节点16为负荷所在位置。数据采集与监控SCADA(supervisory control and data acquisition)量测误差的标准差为0.02,设置Holt’s 两参数法的参数为αH=0.95、βH=0.01。在不同粒子数情况下利用UPF 算法进行状态估计的计算时间及精度对比如表2所示。
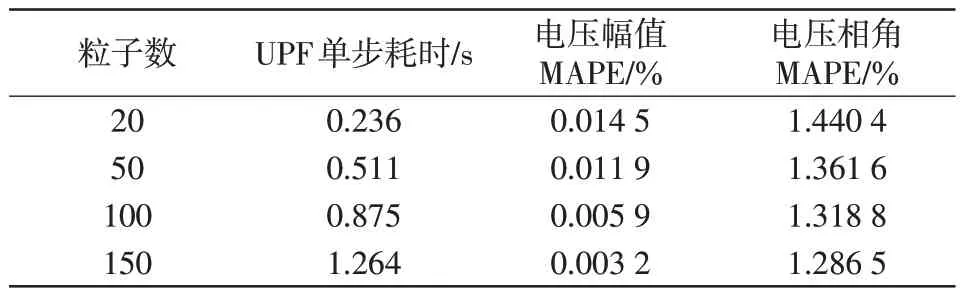
表2 不同粒子数的UPF 算法计算时间及精度对比Tab.2 Comparison of calculation time and accuracy among UPF algorithms with different numbers of particles
由表2可知,随着粒子数的增加,利用UPF算法进行初步状态估计的计算精度变高,而计算时间相应地也会变长。因此,可以根据实际情况灵活调整粒子数,来平衡不同的滤波精度与计算时间要求。
4.4.2 自适应混合动态状态估计仿真分析
在UPF 算法中粒子数设为100 的情况下,状态估计结果如图7和图8所示。使用不同算法的状态估计精度对比如表3所示。
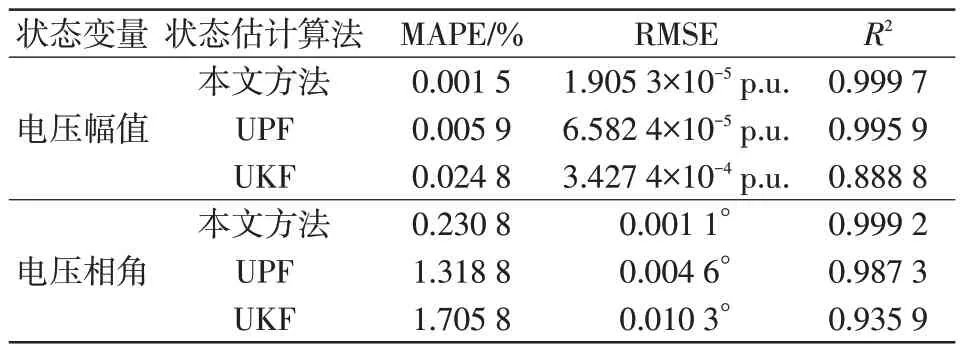
表3 状态估计精度对比结果Tab.3 Comparison results of state estimation accuracy
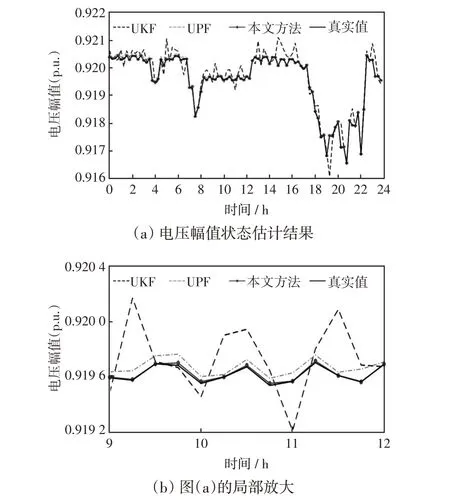
图7 电压幅值状态估计结果Fig.7 Voltage amplitude state estimation results
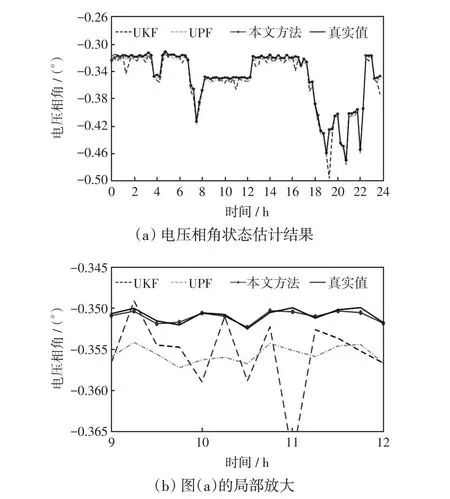
图8 电压相角状态估计结果Fig.8 Voltage phase angle state estimation results
从图7 和图8 可以看出,当晚上进行电动汽车充电时,电压幅值下降较大,相角也有明显改变,此外,本文所提混合动态状态估计方法与真实值最为接近,UPF 算法估计精度次之,UKF 算法偏差最大。这是因为混合状态估计方法融合了UPF 算法结果与预测结果潮流计算值,估计效果良好。根据表3中的数据对比,评价指标可以反映出混合动态状态估计方法的优越性。
4.4.3 有不良数据时混合动态状态估计的抗差分析
假设在14:45时刻量测出现不良数据,节点16注入有功功率量测由-0.005 8 p.u.跳变改为-0.600 0 p.u.。电压幅值和相角状态估计结果如图9 和图10 所示。在14:45 时刻电压幅值和相角的真实值、本文混合状态估计方法预测值、UPF 算法预测值、UKF算法预测值如表4所示。
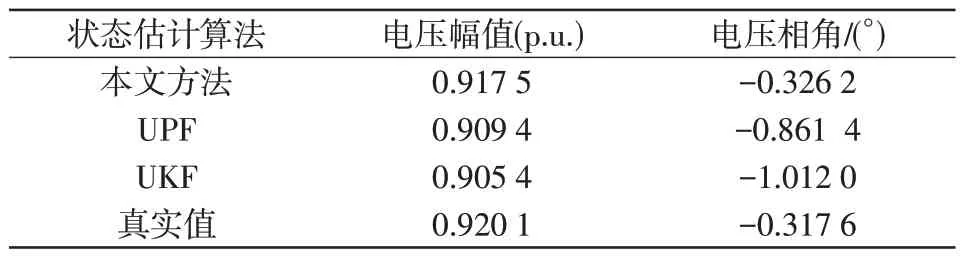
表4 出现不良数据时刻状态变量值Tab.4 Values of state variables in the case of bad data
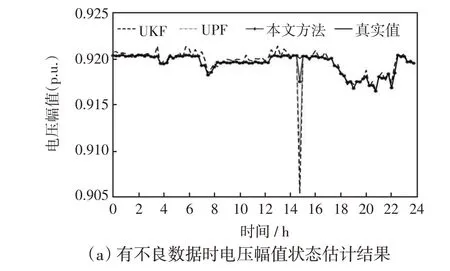
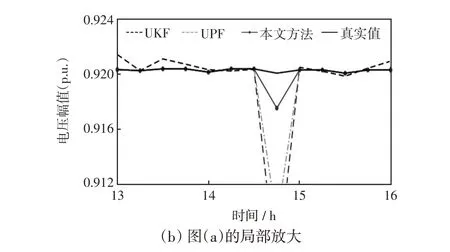
图9 有不良数据时电压幅值状态估计结果Fig.9 Voltage amplitude state estimation result with bad data
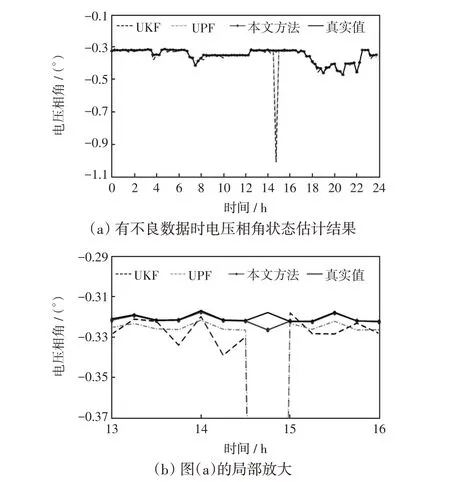
图10 有不良数据时电压相角状态估计结果Fig.10 Voltage phase angle state estimation result in the case of bad data
由图9、图10和表4可知,在14:45时刻量测出现不良数据时,本文的混合动态状态估计方法的抗差性较好,状态估计值与真实值偏离较小,这是因为受到预测结果潮流计算值的影响,使得量测量出现较大波动时状态估计结果的变化较小,而UKF 与UPF算法受量测不良数据影响较大,估计效果较差。
5 结 论
本文提出了一种基于CNN-GRU短期负荷预测和UPF 算法自适应混合的配电网动态状态估计方法,并在IEEE33 节点配电系统的基础上进行了算例分析,得出以下结论。
(1)对于接入电动汽车充电负荷后家庭用电的历史数据,使用CNN-GRU 神经网络模型进行短期负荷预测,可以充分提取负荷数据的特征,预测效果良好。
(2)相比于UKF 算法,UPF 算法在状态估计精度上有了不小的提升,估计误差范围变得更小,但当量测出现不良数据时,状态估计值仍会产生较大的偏差。
(3)基于CNN-GRU 和UPF 的自适应混合动态状态估计方法,可以根据上一时刻的估计误差自动更新本时刻的权重,在保证估计结果实时性的基础上比UPF 算法精度更高。由于引入了负荷预测的结果,在量测量出现不良数据时估计误差更小,鲁棒性更好。
