基于阻抗灵敏度的MMC 稳定性主导影响因素分析

2024-05-07吴晓鸣沈玉明王绪利段修超

电力系统及其自动化学报 2024年4期

吴晓鸣，沈玉明，王绪利，张辉，段修超，池源

（1.国网安徽省电力有限公司经济技术研究院，合肥 230000；2.重庆大学电气工程学院，重庆 400044）

基于模块化多电平换流器的柔性高压直流输电MMC-HVDC（modular multilevel converter based high voltage direct current）技术在分布式能源并网领域得到广泛应用[1-3]。随着直流系统中电力电子设备占比增加，模块化多电平换流器MMC（modular multilevel converter）与互联电网间的宽频谐振问题日益突出，国内外已发生多起宽频谐振事故[4-6]，且不同事故中主导因素存在差异，提高了针对性抑制策略的设计难度。因此，亟需开展MMC 谐振机理的研究，明确主导诱发因素，进而定向提升系统稳定裕度。

现有的MMC互联系统稳定性分析可分为时域状态空间和频域阻抗两类：前者将MMC 完全转化为时域数学模型，建立状态空间矩阵，利用矩阵特征值判断系统稳定性[7-8]，但求解过程复杂，一般用于辅助验证；后者关注MMC端口外特性，采用奈奎斯特判据开展稳定性分析[9-10]，因其建模简单、易于验证已成为研究MMC互联系统谐振问题的主流手段[11]。针对主流的频域阻抗建模方法，谐波状态空间和多谐波线性化各有优劣，可适当中和。文献[12]用谐波状态空间对MMC控制环节模块化建模，但稍显复杂；文献[9]采用多谐波线性化的方式建立交互系统阻抗模型，频率特性清晰，但控制环节的拓展性差。基于现有时、频域模型，文献[13-14]侧重对建模结果定性分析，研究参数变化对系统稳定性的影响；文献[15]则改进两电平换流器的谐振抑制策略用于MMC，并利用阻抗模型进行验证，但谐振主导因素不请晰，抑制效果有待优化。综上，尽管缺乏具有针对性的主动谐振抑制策略，但时频域稳定性研究已有较成熟的建模基础，可为后续定量评估系统谐振主导影响因素提供模型支撑。

目前，在针对MMC 与互联系统稳定性主导影响因素的分析中，最为简便的方法便是根据工程经验和控制器的主要控制频段来定性分析[16]，但仅通过对比不同参数下系统的稳定性差异，无法准确给出参数对于互联系统稳定性的影响趋势，且工况改变会使结论的可适性变差。因此，文献[17-18]从时域分析法的角度出发，进行参与因子分析，确定系统稳定性的主导影响因素；但该方案仅针对已有谐振趋势的固定模态进行主导因素定量分析，所研究频率单一无法应用于MMC全频段稳定性分析，难以指导控制系统初始设计。由以上分析可知，在利用工程经验或时域稳定性判别方案进行稳定性主导因素研究时，二者应用效果有待优化，目前仍缺乏针对MMC宽频段谐振主导影响因素定量分析的方法。

为解决上述问题，本文给出MMC宽频阻抗模型，利用阻抗灵敏度分析方法，提出适用于宽频领域的谐振稳定性主导因素分析策略。首先，对互联系统划分频段，采用谐波状态空间和多谐波线性化相结合的手段建立MMC宽频阻抗模型；然后，提出MMC阻抗绝对灵敏度与标幺灵敏度计算方法，定量得出不同影响因素对于MMC互联系统阻抗塑造和稳定性改善的贡献程度；最后，确定各频段的主导影响因素，并通过Matlab/Simulink对所建立的MMC宽频阻抗模型和阻抗灵敏度计算结果进行仿真验证。

1 MMC 换流器宽频阻抗建模

为降低建模难度，本文将MMC 划分为中低频和高频段建模，即以300 Hz 为临界点，各频段主要考虑的控制结构框图如图1 所示。由于MMC 的阻抗建模较为成熟，为使MMC高低频段阻抗特性与建模手段间更加匹配，本文在中低频段参考文献[12，19]采用谐波状态空间法，而在高频段采用多谐波线性化策略[9，14]建立MMC 宽频阻抗模型，并利用Matlab/Simulink进行仿真验证。

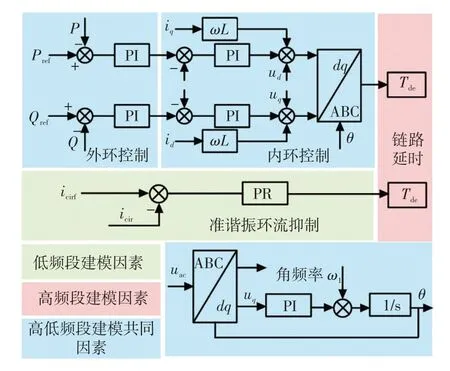
图1 MMC 控制结构框图Fig.1 Block diagram of MMC control structure

图1 中，Pref、P分别为有功功率的参考值和实测值；Qref、Q分别为无功功率的参考值和实测值；icirf、icir分别为桥臂环流的参考值和实测值；id、iq分别为d、q轴电流分量；uac为三相交流电压；uq为q轴电压分量；Tde为链路延时；θ为相角，ω1为角频率；ωL为电流解耦项。

1.1 基于谐波状态空间的MMC 中低频段阻抗建模

基于谐波状态空间的阻抗建模理论，对MMC中低频段建模，其基本流程如图2所示。

图2 MMC 中低频段阻抗建模流程Fig.2 Flow chart of impedance modeling for MMC in low-and medium-frequency bands

图2 中，x为状态变量；y为输入量；E、F为稳态参数；t、s分别为时域和频域。为实现阻抗建模除图1给出MMC的控制结构外，还需要主电路的拓扑结构，本文采用的半桥型MMC拓扑结构如图3所示。

图3 MMC 拓扑结构Fig.3 Topology structure of MMC

图3 中，MMC 拓扑由三相6 桥臂组成，每个桥臂中含有N个串联的子模块SM（T1和T2为开关管），一个桥臂电抗器Larm和电阻Rarm，其中的Carm为每个子模块电容；Idc为直流母线电流，ugdc为直流侧等效电源，Zgdc为直流侧等效阻抗；Zgac为交流电网阻抗；uu,j、ul,j分别为j相上、下桥臂电压，iu,j、il,j分别为j相上、下桥臂电流，iac,j为交流侧j相电流，ugac,j为交流电网侧j相电源电压，uj为MMC控制输出的j相电压，j=A、B、C；O、O′分别为交、直流侧中性点。

本文以MMC 三相对称运行为分析基础，将三相建模简化为A相单相建模，以下公式中则省略下标A。为便于分析影响因素，参考图2 将建模过程分为主电路与控制电路建模两部分。

1.1.1 中低频段主电路部分建模

基于图3的MMC拓扑结构，利用基尔霍夫电路定理对上、下桥臂分别处理，可得基本回路方程。进一步将该方程做小信号处理，可以得到电路小信号方程，为方便引入控制系统，将小信号方程进行差共模处理可得

式中：Δugdc、Δugac分别为直流侧和交流侧电压的小信号扰动量；Δucm、Δudm分别为桥臂电压共模和差模的小信号扰动量；Δicm、Δiac分别为桥臂电流共模和交流并网电流的小信号扰动量。

共、差模变换的具体定义可表示为

式中：xu、xl分别为需要变换的上、下桥臂电气量；xcm、xdm分别为变换后的共、差模量。

由于中低频段阻抗受MMC 动态特性影响显著，考虑电容动态可以得出关于MMC 小信号模型的补充方程为

式中：Δmcm为共模调制波扰动量；Δmdm为差模调制波扰动量；ΔuCcm为共模电容电压扰动量；ΔuCdm为差模电容电压扰动量。

利用傅里叶级数展开，可以将时域模型转换至频域。为保证转换前后的等效性，所有稳态值均为托普利兹矩阵的形式，扰动量为对角矩阵的形式。

1.1.2 中低频段控制电路建模

以功率外环和电流内环的MMC双闭环控制为例，在考虑内外环控制与环流抑制策略时，可以对MMC的控制环节建模为

式中：GI、GP和Gcir分别为电流内环、功率外环和环流抑制控制器；Kx为电流解耦项，为满足时频变换要求，所有控制器均为对角矩阵的形式；Δid、Δiq分别为扰动d轴和q轴电流；ΔP为扰动功率；Δicm为扰动共模电流。

当考虑锁相环对系统的影响时，参考文献[12]对锁相环部分的小信号建模，其结果可表示为

式中：Δθ为扰动相位差；Δugac为交流扰动电压；Tdq为Park变换的频域形式；ωp为扰动角频率；GPLL(ωp)为锁相环控制器GPLL的频域表达式；KpPLL、KiPLL分别为锁相环控制器比例和积分系数的HSS表达式；U1为基频电压幅值；j为虚数单位。

1.1.3 中低频段阻抗表达式

主电路与控制电路合并，可得考虑MMC 内部动态及各控制环节的完整小信号模型为

式中：Δugdc为直流扰动电压；H、G为中间系数矩阵，限于篇幅，其具体表达式及求解过程可参考文献[12，19]。

寻求扰动电压电流关系可分别得到MMC 的交、直流阻抗ZAC_MMC、ZDC_MMC为

1.2 基于多谐波线性化的MMC 高频段阻抗建模

在MMC 高频段阻抗建模时无需考虑内部动态，着重考虑链路延时对阻抗影响。鉴于高频段主电路不变，但控制环节减少，可采用更简洁的多谐波线性化方法进行控制部分建模。多谐波线性化建模基础理论仍为小信号与傅里叶级数展开，优势在于变量的幅值和频率信息可直接代入表达式中，更易理清频率传递关系。

1.2.1 延时环节的等效建模

中国书画千年历史，不能断了香火，后辈学子首先是在老祖宗灵位前嗑头下跪，老老实实把老师那点东西学到手，添油加柴，把家传本领好好学到家。

实际在MMC 控制中包含诸多延时，本文为使延时环节更加贴近实际工程，采用四阶Pade近似延时环节GTd，具体表达式为

式中：R（s）为Pade 逼近多项式；v、w分别为R（s）分子和分母的阶数；Nv、Nw分别为R（s）分子和分母；τ=Tde为延时大小；ai、bi为i次近似系数，上限为w，为简化计算，令w=4、v=w。

1.2.2 双闭环控制环节建模

对锁相环进行频域小信号分析可得

式中：Upm为交流扰动电压的幅值；TPLL为锁相环开环控制函数；fp为注入扰动频率；f1为工频50 Hz。式（11）与式（6）、（7）对比可知，二者结果一致，仅存在表达形式的差别。

同理，对双闭环控制系统利用多谐波线性化进行建模，考虑功率外环控制器GP、电流内环控制器GI、电流解耦系数Kx与锁相环的影响，可以得出控制系统输出电压参考值uref为

式中：φi为交流侧电压和电流的相位差；I1、U1分别为稳态交流电流、电压的幅值；Ip为电流扰动量，且Ip=0.5Ip0e±jφip，φip为电流扰动的相位；Ip0为电流扰动的幅值；ud0、uq0为中间参数。ud0、uq0的表达式可表示为

式中，id0、iq0分别为基频网侧电流的d、q轴输出量。

考虑控制部分的电压调制比关系，对控制环节输出参考电压uref与实际调制波mdm之间借用MMC直流等效电压ugdc进行转换，其关系为

参考文献[14]的计算步骤，联立MMC的主电路和控制系统频域模型，可以计算出高频段MMC 换流站交直流侧阻抗分别为

1.3 宽频阻抗建模仿真验证

为验证宽频段MMC 阻抗建模的准确性，本文基于附录表A1中的参数，利用Matlab/Simulink平台搭建时域仿真模型，并对MMC 的交直流侧阻抗进行扫频验证，仿真扫频结果如图4 中空心圆，建立的阻抗解析模型结果如图4中实线。

图4 MMC 宽频阻抗验证结果Fig.4 Verification results of MMC broadband impedance

由图4中对应关系可以看出，本文的MMC阻抗建模方案与扫频分析结果高度相符，完全满足谐振稳定性分析的前提条件。

2 MMC 稳定性主导影响因素分析

为快速确定宽频段影响交互系统稳定性的主导因素，基于稳定性判据中MMC幅值尖峰越多，相角负阻尼区间越大，系统越容易失稳的观点，本节提出基于MMC 阻抗模型的主导影响因素分析方法。通过绝对灵敏度研究待分析因素变化时系统阻抗特性的变化趋势，分析阻抗变化对系统稳定性的影响；通过比重标幺化可以得出不同影响因素对系统阻抗塑造和稳定性改善的贡献程度；二者结合可以实现对主导因素的快速定位，并为参数优化方向提供可行性参考。

2.1 MMC 阻抗的绝对灵敏度分析

“阻抗绝对灵敏度”是指某个影响因素作微小变化时系统阻抗的变化量，定义绝对阻抗灵敏度Sk(k,s)的计算公式为

式中：k为影响因素；Δk为因素变化量；s为频域标识；Z为MMC阻抗。

为简化阻抗特性分析，将绝对灵敏度分为幅值灵敏度Sk,Mag(k,s)和相角灵敏度Sk,Pha(k,s)，其分别表示为

式中，Im、Re分别为灵敏度的虚部和实部。

MMC 中低频段和高频段阻抗特性的影响因素有所不同，针对控制器差异本文在进行灵敏度分析时对不同频段分别考虑多种影响因素，如附录图A1所示。

灵敏度分析需要稳定运行点，根据乌东德龙门站工程基本参数并结合文献[20-21]给出的MMC 控制系统参数设计方法，考虑控制系统响应速度等动态性能，可以得到MMC 换流站各参数取值区间如附录表A2所示。

按照式（16）～（18）的绝对灵敏度计算概念，结合附录表A2 的各参数选取区间，利用中低频段与高频段的阻抗模型和附录图A1各频段主要影响因素进行计算，其结果可以分析各因素对MMC 阻抗和交互系统稳定性的影响特性。幅值绝对灵敏度的正负极值点越多、幅值越高及变换越频繁则存在的潜在谐振峰越多；相位灵敏度中极点数越多、幅值越高则负阻尼区间存在的可能性增大。

1）MMC中低频段阻抗的绝对灵敏度分析

以改变电流内环比例系数KpI和积分系数KiI为例，分析在不同电流内环参数下MMC 阻抗幅值和相位绝对灵敏度的变化特性，进而分析参数变化对系统稳定性的影响，其结果如图5所示。

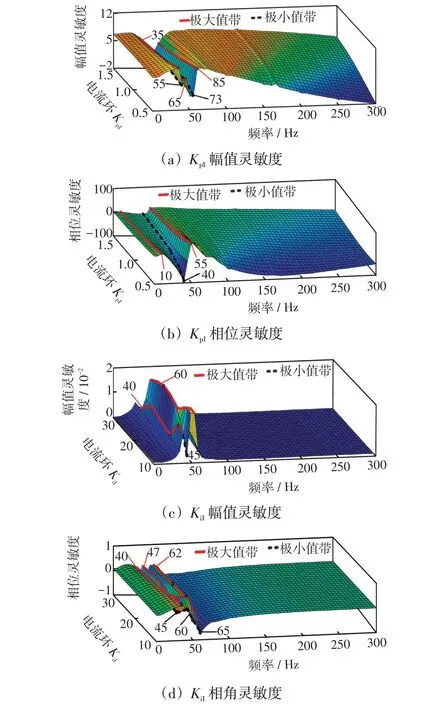
图5 电流内环阻抗灵敏度计算Fig.5 Impedance sensitivity calculation of current innerloop

图5中，加粗实线和虚线带分别为极大和极小值频率带。由图5（a）、（b）可以得出：①MMC的幅值灵敏度在35 Hz、65 Hz和85 Hz处存在极大值，而在55 Hz和73 Hz 处存在极小值，系统的阻抗幅值灵敏度在73 Hz附近存在正负交替，系统易于出现潜在谐振峰，不利于系统稳定；交替点73 Hz 附近幅值灵敏度随KpI的增大而增加，说明降低KpI可以降低该处阻抗变化率，避免尖锐谐振峰的出现，有利于系统稳定。②相位灵敏度在10 Hz和55 Hz处存在极大值，在40 Hz处存在极小值且小于零，系统阻抗的相位在零与极小值间随KpI变化迅速降低，易出现负阻尼现象。

由图5（c）、（d）可以得出：①电流内环比例系数KiI的幅值灵敏度在40 Hz 和60 Hz 处存在极大值点，在45 Hz处存在极小值点略小于零，系统阻抗幅值在极大与极小值切换频率附近可能出现谐振峰。②相位灵敏度在40 Hz、47 Hz 和62 Hz 处存在极大值点，在45 Hz、60 Hz 和65 Hz 处存在极小值点，系统阻抗的相位在小于零的极小值附近迅速下降，易出现负阻尼现象，不利于系统的稳定，增大KiI可以一定程度改善负阻尼现象。

对中低频段阻抗的其他影响因素进行绝对灵敏度分析，并对结果汇总如表1所示。

表1 MMC 中低频段阻抗灵敏度汇总Tab.1 Summary of impedance sensitivity of MMC in low-and medium-frequency bands

表1中，Np为某影响因素下MMC阻抗幅值出现极值次数或相位灵敏度出现极值次数；fp为极值出现频段，极值频率后小括号中的数字代表该频段内极值点出现次数；Mmax、Mmin分别为某影响因素下MMC阻抗幅值灵敏度的最大与最小值，Pmax、Pmin分别为该因素下相位灵敏度的最大与最小值，括号内为极值出现频率；KpP、KiP分别为功率外环的比例和积分系数，Kpcir、Kicir分别为环流抑制的比例和谐振系数。

由表1中各影响因素的灵敏度幅值与极点个数可知，MMC中低频段阻抗特性受电流内环参数、环流抑制器参数、锁相环参数，以及桥臂电感和子模块电容大小影响较大，可以通过优化参数区间提升系统稳定性；而功率外环参数虽然极点较多，但灵敏度幅值较小，优化该参数对提高系统稳定裕度的作用有限。

2）高频段灵敏度分析

高频段的分析过程与中低频段一致，仅影响因素与阻抗模型存在差别，分析结果如附录表A3 所示。由附录表A3 可知，MMC 高频段阻抗受功率外环比例系数、电流内环比例系数、桥臂电感参数和延时环节影响较大，可以通过参数优化提升系统稳定裕度；而受功率外环积分系数、电流内环积分系数和锁相环控制参数影响较小，优化该参数对提高系统稳定裕度的作用十分有限。

2.2 基于标幺灵敏度的MMC 稳定性主导影响因素分析

MMC 的阻抗绝对灵敏度可以分析系统的阻抗特征随各参数及频率的变化情况，得出MMC 各个参数的优化方向；分析绝对灵敏度的极点个数和灵敏度幅值大小也可以一定程度地了解各参数对于稳定性的贡献程度，但由于各影响因素的量纲不同，且极点个数与幅值大小也存在耦合关系，仅通过绝对灵敏度无法明确各个频段中对MMC阻抗特性塑造起主导作用的影响因素。因此本文引入MMC 阻抗特性标幺灵敏度Rk(k,s)计算方法消除量纲影响，横向比较各参数对MMC 阻抗特性的贡献程度，其计算公式可表示为

式中：k、s、Z和Δk的含义同绝对灵敏度中的定义；k0为各影响因素标幺化的基准值，本文以附录表A2各参数运行区间中最大与最小边界的平均阻抗值作为标幺化基准值。

将标幺灵敏度分为幅值和相角两种表达形式，继而利用权重分析法进行变换，得到幅值占比Rk,Mag%(k,s)和相角占比Rk,Pha%(k,s)分别为

式中：Rk,Mag(k,s)、Rk,Pha(k,s)分别为影响因素k下MMC阻抗幅值和相角的标幺灵敏度；Rk,MagΣ、Rk,PhaΣ分别为各频段内所有因素幅值和相角标幺灵敏度之和。对各个频段的影响因子贡献度分析，各频段取影响大小占比前3的因素进行展示，其结果如图6所示。

图6 MMC 宽频段阻抗特性主导影响因子分析Fig.6 Analysis of dominant influencing factors of MMC broadband impedance characteristics

由图6可知，MMC阻抗特性在0～300 Hz频段内的主导影响因素为电流内环比例系数和桥臂电感参数，且随着频率升高桥臂电感的影响程度加深，电流内环比例系数影响程度降低；300～1 000 Hz 频段内的主导影响因素为桥臂电感值，1 000 Hz以上频段系统阻抗特性的主导影响因素为链路延时Tde。

3 算例验证

3.1 阻抗灵敏度验证

为方便验证，本文对控制参数做微小改变后系统阻抗变量进行解析与仿真对比。保持附录表A1中其他参数不变，仅改变电流内环比例系数KpI的取值，分析MMC 系统阻抗幅值与相角的变化情况，选取160 Hz处MMC阻抗对本文提出的阻抗绝对灵敏度计算结果进行时域仿真扫频验证，其结果如表2所示。

表2 中低频段阻抗灵敏度计算结果验证Tab.2 Verification of calculation results of impedance sensitivity in low-and medium-frequency bands

表2中，ΔM为阻抗幅值变化计算结果；ΔP为阻抗相角变化计算结果；ΔM′为阻抗幅值变化扫频结果；ΔP′为阻抗相角变化扫频结果。由表2可以看出，计算与扫频得到的阻抗变化量能够较好地吻合。由于最小步长取0.1，最大的误差在2.5%左右，验证了灵敏度计算结果的准确性，也说明中低频段灵敏度计算结果能够反映MMC阻抗特性的变化规律。

同理对高频段的阻抗灵敏度进行验证，选取2 200 Hz 处MMC 阻抗受功率外环比例系数影响情况进行对比，其结果如附录表A4所示，由附录表A4可以看出，最大误差在3.5%，验证了本文提出的阻抗灵敏度计算方法的正确性，进而说明基于阻抗灵敏度的稳定性主导因素分析方法的可行性。

3.2 主导因素与稳定性验证

限于篇幅，正文仅对中低频段主导影响因素进行验证与详细分析，以此证明本文方案的有效性，而对高频段主导因素的时域验证结果可参考附录图A2。

根据标幺灵敏度权重分析可知，在中低频段电流内环比例系数KpI是稳定性主导影响因素；根据绝对灵敏度可知，减小KpI的值有利于增加系统稳定性，利用奈奎斯特稳定性判据对比KpI为1.5（谐振抑制前）和降低后的0.7（谐振抑制后）时系统的稳定性如图7所示。

图7 谐振抑制前后系统奈奎斯特曲线Fig.7 Nyquist curves of system before and after resonance suppression

由图7 可以看出，降低控制器参数后，系统由原来的包围（-1，0）点变为不包围，按照具体判据可知，改变参数后的MMC 互联系统整体稳定性得到显著提升。

为验证KpI改变前后MMC 互联系统稳定性的变化情况，按照附录表A1 标定的系统参数开展时域仿真。当t=1.0 s 时，向系统中注入幅值为基波电压幅值的1%的扰动源；t=1.1 s 时，将电流内环比例系数由1.5切换至0.7，整个过程系统主要电气量的变化如图8所示。

图8 KpI 改变前后系统主要电气量波形Fig.8 Waveforms of main electrical quantities of system before and after changes in KpI

由图8 可知，在1.1s 降低KpI后系统由谐振转为稳定运行，符合理论分析结论。

同理，依据第2.1 节理论对高频段主导影响因素Tde开展稳定性影响趋势分析可知，在附录表A1所示工况下，降低Tde有利于互联系统的稳定，时域验证结果如附录图A2所示。t=1.0 s时，向系统注入高频扰动，系统开始发生振荡；t=1.1 s 时，将系统延时Tde由700 μs 降为300 μs，系统由谐振转为稳定运行，与理论分析保持一致。

综上可知，本文第2.2 节基于阻抗相对灵敏度的稳定性主导因素分析结论正确，且可以根据第2.1节中绝对灵敏度的变化情况进行针对性的参数设计，提高系统稳定性。

4 结论

本文通过采用划分频段的方法分别利用谐波状态空间和多谐波线性化的方法建立MMC的宽频阻抗模型，仿真结果表明所建模型具有较高的准确度，可作为系统稳定性分析的研究基础。在阻抗模型的基础上，本文提出基于绝对灵敏度和标幺灵敏度的系统稳定性主导因素定量评估方法，明确了MMC互联系统中低频段和高频段的稳定性主导因素。得出以下结论。

（1）对于系统中低频段，在0～50 Hz频段内的主导影响因素为电流内环KpI；在50～100 Hz频段内的主导影响因素为电流内环KpI和桥臂电感Larm；在100～200 Hz频段内的主导影响因素为电流内环KpI和桥臂电感Larm；在200～300 Hz频段内的主导影响因素为桥臂电感Larm。

（2）对于系统高频段，在300～1 000 Hz频段内的主导影响因素为桥臂电感Larm；在1 000 Hz 以上频段系统阻抗特性的主导影响因素为链路延时Tde。

附录A