高碳中锰耐磨钢凝固过程溶质微观偏析模型

2024-05-03刘洪波车晓锐张彩东田志强

工程科学学报 2024年6期

李民，刘洪波，车晓锐，刘颖，张杰，张彩东，田志强，徐浩

1) 河钢材料技术研究院，石家庄 050023 2) 北京科技大学冶金与生态工程学院，北京 100083 3) 北京科技大学工程技术研究院，北京100083

金属材料磨损现象普遍存在于工程机械、冶金矿山、交通运输等领域，据不完全统计，每年因磨损造成的经济损失就高达我国GDP的5%[1-2].近年来，凭借优异的耐磨性能，高碳中锰耐磨钢（简称中锰钢）已被冶金、煤炭、机械、建材等领域认定为指定用钢[3-8].中锰钢是在高锰钢的基础上通过合金化及变质处理得到的，其耐磨性能更优[9-10].然而，在工业生产时中锰钢疏松、缩孔现象较为严重，这与其凝固过程密切相关.

钢的凝固过程是影响产品综合性能的关键工艺之一，不容忽视.在钢的凝固过程中，溶质元素在液、固两相中的溶解度存在差异，导致溶质元素在凝固前沿固、液两相中会发生再分配现象[11]导致微观偏析，由此造成产品成分的差异性，最终恶化产品的力学性能[12].对于中锰钢来说，其合金含量较高，因此在凝固过程中微观偏析行为发生更显著[13-14].近几十年来，众多冶金研究者们通过构建数学模型来深入理解和揭示钢凝固过程中的微观偏析行为.安航航等[15]同时考虑了Ohnaka以及Voller-Beckermann模型，并考虑了δ/γ的相变过程，构建了GCr15轴承钢凝固两相区溶质微观偏析模型，较为准确的预测了220 mm×260 mm大方坯的偏析行为.罗森等[12]综合考虑了δ/γ的相变过程及MnS夹杂析出过程，构建的溶质微观偏析模型与实测零强度温度（ZST）与零塑性温度（ZDT）吻合度较好.以V-B模型为基础，并考虑到凝固温度以及相组成对溶质分配系数和扩散系数的影响，桂林涛[16-17]构建了基于钢中夹杂物析出的溶质微观偏析耦合模型，该模型预测结果与文献中报道相一致，其准确性较高.

由此可见，精准建立溶质元素的偏析模型对于钢凝固过程中的理论分析及实际生产都具有重要意义.然而，目前还未见中锰钢凝固过程微观偏析模型的相关报道.本文通过热力学计算与实验等多种技术手段精准表征了中锰钢凝固过程中特征参数，以此为基础对中锰钢溶质元素凝固过程中的偏析行为进行了剖析，得到了适用于此成分体系下的微观偏析模型，这对于深刻认识中锰钢微观偏析现象，减少中锰钢模铸过程铸锭缺陷，提高中锰钢的成材率以及后续中锰钢连铸过程质量保证具有重要理论和现实指导意义.

1 实验材料及方法

1.1 实验材料

本文所研究的中锰钢在本院中试基地50 kg中频真空感应炉冶炼而成，将铸锭切除冒口后，在铸锭中心出取ϕ30 mm×20 mm部分样品进行光谱测试，钢中主要元素及成分如表1所示.

表1 中锰钢化学成分（质量分数）Table 1 Chemical composition of medium manganese steel%

1.2 溶质微观偏析模型

微观偏析模型的建立是以质量守恒方程为基础，基于不同假设，推导得到可以精准表述溶质元素浓度和固相率之间的数学模型[18].最早提出的偏析模型是基于Lever-ruler原理的杠杠模型（简称Level模型），此模型中假设钢的凝固是一个平衡过程[19]，钢中溶质元素在液固两相中完全均匀扩散，随时都处于平衡态，在凝固过程中残余液相中溶质元素浓度cL与固相率fS之间存在以下关系：

其中，k为溶质分配系数.

然而，实际上大部分溶质元素在液相中的溶解度远超过固相中的溶解度，甚至存在数量级间的差距，因此，钢的凝固实际上都是非平衡态.因此在Scheil-Gulliver模型（简称Scheil模型）[16]中假设溶质元素在固相中完全不扩撒，而在液相中分布均匀，在固液两相的交界处存在局部平衡.此时cL与fS存在如下关系：

虽然在Scheil-Gulliver中考虑到了非平衡态的存在，但是该模型仍有一定局限性，比如当凝固即将完成，即固相率fS接近1时，此时溶质组元的浓度反而为无穷大，与实际凝固过程不符.为了使模型的结果更接近实际情况，后续研究者们考虑了溶质元素在固相中的有限扩散行为，并引入了反扩散系数进行表征，并且针对不同模型，反扩散系数不同的计算方法.

在Brody-Flemings模型（简称B-F模型）[20]中进行了一些基本假设，例如：①枝晶形貌为平板状，且任何时刻都处于热动态平衡态；②溶质元素固相中以体积扩散形式进行；③凝固过程中枝晶间距固定，并假设界面生长形式为抛物线；④凝固收缩导致的密度变化暂不考虑等.通过以上假设，得出的B-F偏析模型的表达式为：

式中：Φ= 2α，α=DStf/L2=4DStf/λ2，其中tf=TL-TS/CR为局部凝固时间，s；TL、TS分别为液、固相线温度，K；CR为冷却速率，K·s-1；L为二次枝晶间距的一半，m；λ为二次枝晶间距，m；DS为固相中溶质扩散系数，m2·s-1；α为溶质组元的反扩散系数.由B-F模型可以发现，当式中DS等于0时，即认为溶质元素在固相中基本不扩散时，此时的B-F模型即为Scheil-Gulliver模型；而当DS接近于1时，即认为溶质元素在固相中完全扩散，此时B-F模型即为Lever-ruler模型.此外，当大于1时，B-F模型则无意义，因此B-F模型也存在一定局限性.

后续学者在B-F模型的基础上通过对反扩散系数进行了不同的修正（对Φ值进行了完善），得到不同的偏析模型.其中Clyne和Kurz[21]（简称C-K模型）将溶质元素在固相中分布当作指数衰减进行处理，得到Φ的关系式为：

而 Kobayashi[22]考虑到枝晶粗化及不规则微观枝晶结构对溶质元素分布的影响，采用积分轮廓法对B-F模型进行修正，此方法中没有对求解扩散方程直接求解，而是对溶质质量平衡方程整体进行求解，修正后的Φ的表达式为：

其中，A为修正系数，钢液当凝固前沿以平板状生产时A=2，以柱状生长时A=4.

最后Won和Thomas[23]在C-K与Ohnaka等模型的基础上综合考虑各组分、柱状枝晶微观结构、相变转化的影响，得到W-T模型中Φ的表达式为：

其中，α+为修正后的α，α+=α+αC，αC为α的碳质量分数的指数函数，由以上分析可知，目前已知的各种微观偏析模型都可以用通式进行表达，各模型的区别在于通式中Φ值的表现形式不同，各个模型对应的Φ值的求解方法见表2所示.

表2 各微观偏析模型及其参数Φ的表达式总结Table 2 Summary of the expression of microsegregation models and its parameter Φ

2 偏析模型中参数的选取

由1.2章节可知，只需已知液相线温度TL、固相线温度TS，二次枝晶间距λ，冷却速率CR，局部凝固时间tf，扩散系数DS，溶质分配系数k等特征参数后，就可以建立相应的各微观偏析模型.

2.1 液、固相线温度确定

中锰钢液、固相线温度通过热力学软件FactSage进行计算得到，本文中采用Factsage8.0版本，数据库选择“FS stel”，计算过程中选择“IL”模式中的“equilibrium cooling”（平衡）凝固模式，将凝固过程中液相中开始析出固相时对应的温度定义为液相线温度，计算得到中锰钢液相线温度如图1所示为1422.93 ℃.固相线温度计算过程中选择IF模式，计算得出对应的固相线温度为1280.98 ℃.

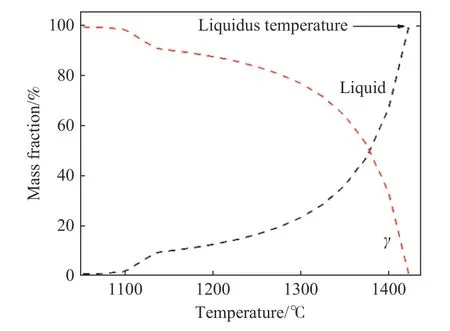
图1 中锰钢液相线温度的确定Fig.1 Determination of the liquidus temperature of medium manganese steel

2.2 二次枝晶间距、冷却速率、局部冷却时间

对于钢的自然凝固过程来说，很难精准计算得到其冷却速率CR及局部凝固时间tf，Won和Thomas[23]等基于大量实验总结得到了有关冷却速率CR、钢中C质量分数MC与二次枝晶间距λ的关系式即：

为获得均质化的二次枝晶组织，在中锰钢铸锭中选取部分试验加工成ϕ5.5 mm×100 mm的圆棒状试样进行凝固实验，本文中定向凝固实验采用DJL-500 Bridgeman定向晶体生长炉进行.实验过程中凝固前沿的温度梯度(G)保持为5 K·mm-1不变，实验过程中以10 ℃·min-1的升温速率将坩埚从室温升至1500 ℃，为确保样品完全熔化，在该温度下保温10 min，将坩埚以抽拉速度V=50 μm·s-1向下抽拉至Ga-In-Sn合金液中进行冷却.待固相凝固到相应长度，组织生长稳定后，将坩埚连同已凝固固相和未凝固液相一同浸入Ga-In-Sn合金液中进行快速冷却以保留固液界面形貌.

定向凝固试样取出后，切取固液两相区然后将试样镶嵌，随后在自动磨样机上进行磨、抛处理后，采用4%硝酸酒精中进行腐蚀，然后采用激光共聚焦显微镜对其固液界面形貌进行观察，可明显在固液两相区观察到二次枝晶如图2所示，采用IPP软件统计200张以上二次枝晶间距，在此实验条件下，中锰钢二次枝晶的正态分布如图3所示.然后对其取平均值得到此冷却速率下的二次枝晶间距为59.77 μm.

图2 拉速为50 μm·s-1时中锰钢定向凝固试样纵截面形貌图Fig.2 Optical macrostructure of directionally solidified samples in longitudinal section with pulling speeds of 50 μm·s-1

图3 拉速为50 μm·s-1时中锰钢定向凝固试样二次枝晶间距分布图Fig.3 Frequency distribution of the (Secondary dendrite arm spacing)SDAS of the directional solidification samples of medium manganese steel the pulling speeds of 50 μm·s-1

在已知液、固相线温度、冷却速率等特征参数时，局部冷却时间可根据公式（8）所示进行求解.

2.3 溶质分配系数及扩散系数

在微观偏析模型中，溶质分配系数ki决定了在钢液凝固过程中溶质元素i在固、液两相间的再分配趋势[24].在凝固过程中，当ki＜1时，此溶质元素i将由固相向液相中富集，最终表现为溶质元素i发生正偏析行为；而当ki＞1时，溶质元素i将由液相向固相中富集，最终表现为溶质元素i发生负偏析行为；ki=1时，不会发生溶质再分配现象，即不发生正偏析也不发生负偏析[25].尽管在实际凝固过程中，ki与钢中溶质组元含量、凝固温度、相组成密切相关，其真实值并不为一个定值[26].然而，刘洪波[19]采用Thermo-calc热力学软件得到对Fe-17.72Mn-0.60C-1.47Al高锰TWIP钢的溶质分配系数计算发现，温度对ki的影响较小，其研究得到不同温度下的平均值为0.776，而Choudhary和Ghosh[27]通过研究发现Mn的ki为0.785，两者差距较小，因此为简化模型的计算过程在本文中锰钢中Mn的分配系数当作定值进行处理.

扩散系数通常由Arrhenius公式进行求解，如公式9所示，扩散系数D主要受凝固前沿温度的影响较大.此外，D在不同相如液相中（DL）与固相中（DS）取值有所区别，并且在固相中的铁素体相（Dδ）与奥氏体相（Dγ）也存在差异.

其中：D为对应凝固温度下的扩散系数，cm2·s-1；D0为频率因子，cm2·s-1；Q为活化能，J；R是理想气体常数，8.314 J· mol-1·K-1)；TL-S为凝固前沿温度，K.扩散系数的选择同样选择文献中报导值.

前文提到，溶质分配系数ki与扩散系数D的选取与钢的相组成也有关，同一溶质元素在δ与γ之间的ki与D也存在差异[28]，因此必须确定中锰钢凝固模式.本文采用Factsage计算了不同Mn及Cr含量下的中锰钢的凝固模式，如图4所示（FCCA1、FCC-A1#2代表不同类型的奥氏体相），中锰钢的凝固模式为L→ L+ γ →γ属于奥氏体凝固模式，无包晶反应的发生，也无其他相的出现，并且随Mn以及Cr含量的增加，凝固模式也并未发生改变.因此可以确定在奥氏体凝固模式下溶质分配系数ki与扩散系数D的选取如表3所示.

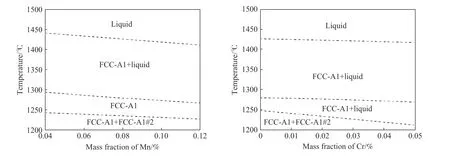
图4 中锰钢凝固模式计算.（a）Fe-0.95C-(4～12)Mn-0.2Si-2.1Cr-0.035Nb-0.065V-0.32Mo-0.01Al 凝固模式计算; （b）Fe-8.5Mn-(0～5)Cr-0.95C-0.2Si-2.1Cr-0.035Nb-0.065V-0.32Mo-0.01Al凝固模式计算Fig.4 Calculation of the solidification model of medium manganese steel: (a) solidification model of Fe-0.95C-(4-12)Mn-0.2Si-2.1Cr-0.035Nb-0.065V-0.32Mo-0.01Al; (b) solidification model of Fe-8.5Mn-(0-5)Cr-0.95C-0.2Si-2.1Cr-0.035Nb-0.065V-0.32Mo-0.01Al

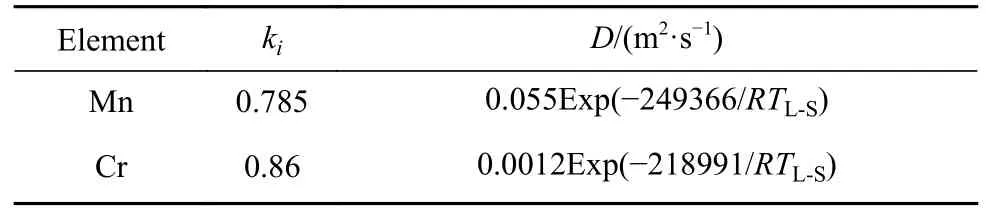
表3 中锰钢凝固过程溶质分配系数及扩散系数[27]Table 3 Solute distribution coefficient ki and diffusion coefficient Di of medium manganese steel during solidification[27]

如表3所示，扩散系数此时只与凝固前沿温度TL-S相关，而TL-S随着凝固的进行不断变化，其与液、固相线温度关系式如公式（10）所示：

其中：TL为液相线温度，本文中取值1695.85K；TS为固相线温度，本文中取值1554.13K；Tm为纯铁的熔点，本文中取值1811K；fS为固相率.

3 偏析模型的构建与验证

3.1 偏析模型构建

在钢的凝固过程中，二次枝晶既在垂直于一次枝晶臂方向生长的同时，也沿二次枝晶的中心轴线向二次枝晶两侧生长，元素偏析程度在后者更为明显，因此在沿着垂直二次枝晶中心轴线方向任一侧等距打点，进行点扫描，以分析各元素在枝晶内的分布情况，具体打点位置如图5所示

图5 中锰钢电子探针形貌及其点扫描示意图.（a）二次枝晶形貌；（b）二次枝晶点扫描示意图Fig.5 Electron probe morphology and diagrams of point scanning of manganese steel: (a) secondary dendrite morphology; (b) schematic of secondary dendritic point scanning

在点扫描过程中各位置元素含量结果如图6所示.从图中可明显看出，随着凝固过程的进行，钢中Mn、Cr元素含量不断增大，Mn、Cr元素质量分数分别由位置1的9.13%与2.03%下降到位置10的7.49%与1.68%.即在二次枝晶边缘处Mn、Cr元素的含量高于二次枝晶中心处的含量，这表明在中锰钢凝固过程中Mn、Cr元素含量发生明显的正偏析行为.

图6 中锰钢定向凝固电子探针点扫描实验结果Fig.6 Experimental results of electron probe point scanning for the directional solidification of medium manganese steel

根据本文3.2章节中所述溶质微观偏析模型，以及后续各特征参数对中锰钢凝固过程中Mn、Cr元素的偏析行为进行剖析，得到Mn、Cr元素的偏析指数ρi随凝固过程的变化规律，并与EPMA点扫描结果进行对比验证.

3.2 分析与讨论

前文提到，在凝固过程中，二次枝晶以其横向轴线为中心向枝晶边缘对称生长，因此，认为电子探针实验中横向轴线任意一点为凝固过程中的起点（图5（b）中的点10），此时对应凝固分数为0%，二次枝晶边缘为凝固过程终点（图5（b）中的点1）此时对应的凝固分数为100%，对表2中各微观偏析模型计算值与EPMA电子探针实测值进行对比分析.

在定向凝固温度梯度为5 K·mm-1，抽拉速度为50 μm·s-1时，Scheil模型的计算结果与EPMA测试值相差较大，尤其是当固相分数接近于1时，Sccheil计算结果接近2.2远高于EPMA测试结果.而Lever、B-F、C-K、Ohhnaka与W-T模型在固相分数较小时相差不大，随着凝固进行，W-T模型测试结果逐渐增大，B-F测试结果最小.图7为中锰钢定向凝固过程中二次枝晶内Mn元素偏析指数随固相分数的变化，从图7（b）中的放大图中可看到，B-F偏析模型与EPMA实测值最相近，因此针对本文中锰钢的成分与凝固条件，可通过B-F模型预测Mn元素的偏析行为.

图7 中锰钢定向凝固过程中二次枝晶内Mn元素偏析指数随固相分数的变化.（a）偏析模型计算结果与EPMA对比；（b）偏析模型放大图Fig.7 Changes in the Mn segregation index in secondary dendrites with solid phase fraction during directional solidification of medium manganese steel:(a) comparison between the results of the segregation model and EPMA; (b) enlarged view of the segregation model

图8为Cr元素偏析模型与EPMA实测值的对比结果.从图8（a）可知，在固相分数较小时，Scheil模型计算结果大于EPMA实测值，随着凝固的进行Scheil模型计算结果偏大，在固相分数接近于1时，Scheil模型计算结果远高于实测值.而B-F模型的计算结果与Scheil正好呈相反的趋势，在固相分数较小时，B-F模型计算结果大于EPMA实测值，而当固相分数较大时，B-F模型计算结果却低于EPMA实测值，其余模型如Lever、C-K、Ohnaka、W-T模型计算结果相差不大.由图8（b）的放大图可知，从整体来看Cr元素EPMA实测值结果与C-K模型的计算结果最为接近，因此在本文中凝固条件下可采用C-K模型对Cr元素的偏析行文进行预测.

图8 中锰钢定向凝固过程中二次枝晶内Cr元素偏析指数随固相分数的变化.（a）偏析模型计算结果与EPMA对比；（b）偏析模型放大图Fig.8 Changes in the Cr segregation index in secondary dendrites with solid phase fraction during directional solidification of medium manganese steel:(a) comparison between the results of the segregation model and EPMA; (b) enlarged view of the segregation model