基于迭代卡尔曼滤波器的GPS-激光-IMU融合建图算法

丛明 温旭 王明昊 刘冬

（大连理工大学 机械工程学院，辽宁 大连 116024）

自从20世纪80年代同步定位与地图构建的概念被提出以来，其始终是机器人自主导航的核心技术，广泛应用于无人车、无人机等领域。SLAM（同步定位和地图构建）问题的核心内容可以理解为移动机器人是否可以放置在未知环境中，然后逐步构建该环境的地图，同时使用地图来确定其全局位姿［1］。经过多年的努力，目前基于激光雷达和基于视觉的方案均能实现精确的定位和建图功能。虽然视觉方案具有成本低、采集信息丰富和便于回环检测的优点，但是由于对初始化和光照变化敏感而且还要消耗资源计算深度信息，因此不适合于室外环境。激光雷达不仅没有上述缺点，而且高分辨率的三维激光雷达对于环境信息的捕捉能力也越来越强，因此在室外环境中基于激光的算法是更合适的选择。

激光SLAM的里程计算法通过匹配相邻帧的点云数据解算位姿。Besl等［2］提出了迭代最近点算法（ICP），该算法成为了点云匹配发展的基础。但是ICP忽视了点云数据中的几何信息。为了克服这个问题，Segal等［3］提出了G-ICP算法，将残差定义为点到对应平面的距离。Zhang等［4］在G-ICP的基础上提出了LOAM算法，增加了角点特征，进一步扩展了特征点的类型。LOAM的一系列衍生算法［5-8］延续了提取点云数据中的特征点并构建特征点与线和平面之间的约束关系的方式，但是特征提取也增加了对算力的要求。虽然在一些场景中仅使用激光雷达可以实现建图和定位功能，但是在剧烈运动或长廊等场景下算法精度会迅速下降。为了提高里程计的精度和鲁棒性，激光通常和其他传感器融合共同估计机器人状态。

多传感器融合设计方案通常有松耦合和紧耦合两种方式。在LOAM［4］和LeGO-LOAM［5］中，因为惯性测量单元（IMU）仅被用来去除点云运动畸变和提供优化的初值并不参与优化过程，所以属于松耦合方案。松耦合的另一种实现方式是基于滤波方法融合多个传感器各自独立的结果得到一个更加精确的机器人状态。Lynen等［9］提出了基于扩展卡尔曼滤波器（EKF）的通用和模块化的多传感器融合框架。Zhen等［10］使用误差状态卡尔曼滤波器（ESKF）融合IMU测量和粒子滤波器输出的激光里程计。虽然松耦合易于实现，但是紧耦合算法往往能够得到精度更高的结果。Gao等［11］分别设计了GPS和激光的紧耦合算法和松耦合算法，实验表明紧耦合系统的精度优于松耦合系统。Ye等［12］提出了基于优化方法的激光-IMU紧耦合算法，但由于计算量过大，对计算平台要求很高。在LIO-SAM［6］中，将点云匹配得到的里程计因子、IMU预积分［13］因子、回环因子和GPS因子在Isam2［14］上进行联合优化，虽然可以得到准确的结果，但是计算成本很高。在FASTLIO［15］中，采用迭代卡尔曼滤波器处理误差状态，联合优化IMU和激光数据。FAST-LIO2［16］在FASTLIO的基础上使用了优化库［17］，提高了程序的易读性。FAST-LIO2在时间效率方面优于LIO-SAM，而且达到了与LIO-SAM相似或更好的精度。但是由于FAST-LIO2采用增量kd树［18］管理地图，不方便进行回环检测。而且没有融合GPS信息，在大尺度场景下会出现严重的误差累积问题。

虽然目前被提出的算法在多种场景中已经能够很好地完成定位和建图任务，但是在大尺度的室外场景下往往会遇到两个主要的挑战：①特征稀疏的场景会导致轨迹跟踪失败。激光雷达通过接收被障碍物反射回来的激光从而计算周围环境中障碍物到自身的距离。当障碍物距离激光超过150～200 m甚至没有障碍物时点云数据不足以推算轨迹，导致里程计出现较大误差。②累计误差会对算法表现造成严重影响。虽然里程计在短时间内精度很高，但是大尺度场景下累计误差尤其是高程误差会极大影响轨迹推算的结果。在无法构建有效的回环约束的场景下，这种情况更加明显。为了解决以上的问题，本文提出了一种GPS-激光-IMU融合建图算法。

本文的主要贡献有：①设计并实现了一种基于IKF（迭代卡尔曼滤波器）的GPS-激光-IMU紧耦合里程计算法，通过融合GPS的绝对位置信息可以纠正激光-IMU里程计的累计误差，并且可以在特征稀疏的场景下提高算法的鲁棒性；②将重力的优化转化为旋转矩阵群上的优化，解决了重力过参数化的问题。在ENU坐标系下重力方向是沿着Z轴反方向而且在地区不变时重力的模长是稳定的，因此可以将对重力变量的优化视为东北天坐标系（ENU）和世界坐标系之间的旋转关系的优化，将重力的优化在旋转矩阵群上解决；③在室外场景下对算法进行了充分的评估，并且验证了算法在大尺度室外场景下的鲁棒性和精度。

1 算法框架

本文提出的算法通过输入三维激光点云、IMU数据和GPS数据估计机器人位姿并且构建周围环境地图，如图1所示，总体框架由数据预处理、状态估计和后端优化3部分组成。

图1 算法结构图Fig.1 Structure of the algorithm

1）数据预处理。该模块主要对点云和GPS数据进行操作。由于激光对各点的采样存在时间差，因此需要使用IMU数据解算位姿将一帧激光中的所有点云数据都变换到采样结束时刻。输入系统的GPS数据是在LLA坐标系下，因此需要将其转换到ENU坐标系下。

2）状态估计。使用IKF算法融合IMU、激光和GPS数据，估计机器人状态。首先使用IMU数据传递机器人状态，然后计算激光点云数据和GPS数据的残差并更新机器人状态，输出当前时刻的位姿估计，同时也为后端优化提供良好初值。

3）后端优化。由于相邻帧激光点云数据有很大一部分是重叠的，因此采用管理关键帧的方式管理点云数据可以极大提高算法效率。目前扫描上下文（SC）描述子［19］、强度扫描上下文（ISC）描述子［20］和方位直方图强度特征（ISHOT）描述子［21］是广泛使用的描述子，本文采用SC全局描述子检测回环。通过Isam2算法融合回环因子与里程计因子，修正全局位姿并更新全局地图，新的全局地图作为下一次点云匹配的基准。

本文所做的工作主要集中于状态估计部分，以下内容围绕状态估计模块展开。

2 状态估计

2.1 状态转移模型

如图2所示，在本文中世界坐标系记为G，以IMU坐标系为机器人坐标系记为I，初始时刻G坐标系与I坐标系重合。记ENU坐标系为E，通过旋转变换可以将G坐标系变换到E坐标系。机器人的状态x、机器人的误差状态δx、IMU测量u和噪音w分别为

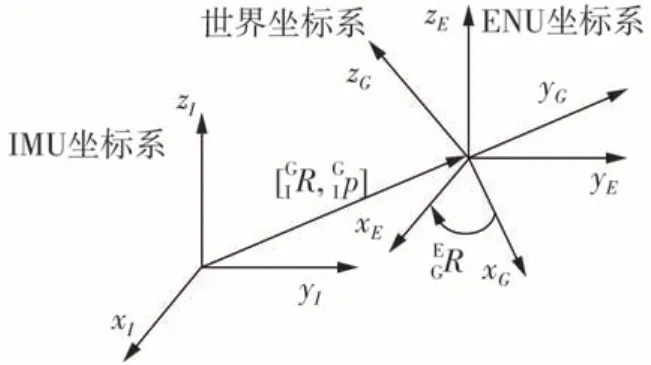
图2 不同坐标系之间关系Fig.2 Relation between different coordinate systems

2.1.1 重力优化

Sola［22］设计了基于误差卡尔曼滤波器的里程计框架。Sola将重力视为三维向量进行优化，但是由于重力是二自由度向量，这将导致重力过参数化和协方差矩阵奇异性的问题。而且优化后为了保证重力的模长不变需要归一化处理。在FAST-LIO2算法中，将重力在流形空间S2中优化从而保证重力模长稳定。

如图3所示，在东北天坐标系（ENU）中重力的方向始终指向地心而且在某一区域运行时重力的大小不会发生明显改变，因此在本文算法应用的场景中可以将重力视为常量。对重力进行优化是为了准确去除IMU测量的加速度中的重力分量。由上文可知东北天坐标系与世界坐标系之间的旋转关系为，因此按照式（2）将世界坐标系下的重力gG转换为的形式：

图3 东北天坐标系示意图Fig.3 Illustration of local Cartesian coordinate system

式中，gG、gE分别为世界坐标系和ENU坐标系中的重力向量。这样处理重力能够充分利用ENU坐标系中重力的物理性质，将重力的优化问题视为ENU坐标系和世界坐标系之间的旋转优化问题，即将对gG的优化转化为对的优化，继而将重力的优化在旋转矩阵群上解决，避免了直接对重力的运算，从而保证了重力模长不变。而且这种优化方式建立起ENU坐标系和世界坐标系之间的约束加深了机器人各个状态之间的耦合程度，因此状态估计的精度得到提高。与FAST-LIO2中的优化算法相比，本文提出的算法更加简洁、计算量更低。

2.1.2 误差状态转移模型

机器人状态的动力学模型为

[a]∧表示向量a∈R3的反对称向量积矩阵，

记i为IMU测量的索引，误差状态的转移模型［22］为

式中：Pi为δxi的协方差矩阵；Pna、Pnω、Pnba和Pnbω分别为噪音na，nω，nba和nbω的协方差矩阵；Fxi、Fwi和Qi按如下公式计算：

式中，R{}为旋转向量对应的旋转矩阵。

2.2 观测模型

在本文提出的迭代卡尔曼滤波器中包括两种观测，使用激光点云数据和GPS数据作为观测更新机器人状态。依靠激光点云数据推测的轨迹光滑而且在短时间内精度很高，但是由于点云匹配是通过将当前帧和历史帧点云进行匹配，因此不可避免地带入了误差的累积。根据GPS数据推算的机器人位姿虽然没有被历史结果影响，但是整条轨迹并不连续。因此两种观测可以互相弥补各自的缺点。

2.2.1 GPS观测

由于输入系统的GPS数据是在LLA坐标系下，因此首先将GPS数据转换到ENU坐标系下［23］。将ENU系下的机器人位置观测记为ygps，观测误差记为vgps，则观测方程和残差rgps分别为

观测方程对机器人状态x的雅可比矩阵H：

2.2.2 激光观测

由于激光一般是按顺序对点采样，所以连续的激光点之间存在一定的时间差。因此伴随机器人的运动，一组激光点云中的数据并不是在同一位姿下采集的，所以首先要对点云进行去畸变。基于IMU数据可以推算出每个激光点相对于当前帧激光点云结束时刻的位姿关系，然后将所有的点变换到结束时刻。

历史帧的激光点云数据有很大一部分是重叠的，因此只保存关键帧的数据不仅不会丢失数据而且会提高算法效率。通过最近邻算法搜索到n个距离当前位姿最近的关键帧{F1，F2，…，Fn}，将n个关键帧的点云数据融合成点云地图M：

记k为激光点云的索引，pL为第k帧激光中的点。qj(j=1，2，3，…，m)为点云地图M中距离pL最近的m个激光点，如图4所示，根据qj计算出pL对应平面的方程为

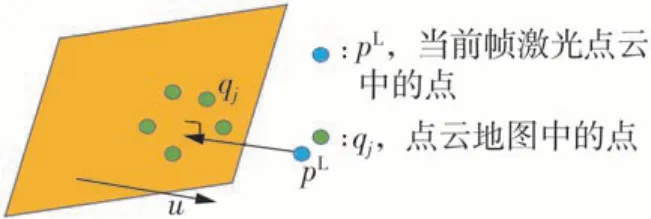
图4 激光观测模型Fig.4 Laser measurement model

vlaser为观测的误差，以pL到对应平面的距离为观测，则观测方程和残差rlaser为

观测方程对机器人的状态x的雅可比矩阵H为

2.2.3 迭代卡尔曼滤波器

在线性高斯系统中卡尔曼滤波器可以得到状态的最优无偏估计，但是在非线性系统中应用EKF（扩展卡尔曼滤波器）需要计算观测方程在线性化点对状态的雅可比矩阵，这样便能将非线性系统线性化，继而估计状态。因此线性化点的选择很大程度上影响了EKF的性能。线性化点越接近状态的真值，状态估计的结果就越精确。当第k帧观测被输入系统时，根据状态转移方程估计的状态为，在EKF中将视为线性化点计算观测方程的雅可比矩阵H，更新状态得到后验估计（j为迭代次数）。IKF将每次得到的后验估计作为线性化点重新估计状态直到收敛。

本文采用针对误差状态的IKF，状态转移方程可以得到两个状态：和，分别为标准状态和误差状态的先验。～N(0，)并且满足关系xk=+。以GPS数据和激光点云数据为观测计算雅可比矩阵H和卡尔曼增益K并更新然后以为线性化点重新线性化观测方程。因为重新选择了线性化点，因此误差状态也需要重新计算［16］，计算公式为

式中：θ为R对应旋转向量的模长；a为R对应旋转向量的单位向量；迭代次数j=0时，Jj为单位矩阵。采用FAST-LIO中的卡尔曼增益计算公式能够避免高维矩阵求逆运算，降低计算成本，因此迭代卡尔曼滤波器的增益和更新方程为

式中，r为GPS和激光观测的残差，R为观测误差vgps和vlaser的协方差矩阵。在迭代卡尔曼滤波器中不断迭代计算卡尔曼增益和雅可比矩阵并且更新机器人状态直到收敛。

3 实验

为验证本文提出算法的有效性，本节介绍在普通场景和大尺度场景下的实验及对应的分析。实验的计算平台为配备了Ubuntu18.04 ROS Melodic，Intel（R）Core（TM）i7-11800H CPU以及16 G内存的笔记本计算机。自建小车硬件平台中搭载的激光雷达为速腾聚创公司的RS-LiDAR-16，IMU和GPS的型号为阿路比公司的LPMS-IG1P，上位机采用大疆公司的妙算Manifold 2-C，硬件的安装位置如图5所示。实验包括：普通场景下对比其他算法与本文算法的建图精度、室外大尺度场景下验证本文算法的建图效果等。普通场景下的实验采用公开数据集，室外大尺度场景下建图使用的数据由搭载16线激光雷达、九轴IMU和GPS的小车采集，硬件平台如图5所示。

图5 自建移动平台Fig.5 Platform of self-build mobile vehicle

3.1 普通场景下建图结果对比

首先对比在融合GPS数据时各算法的精度。使用LIO-SAM文献［6］中的开源数据集序列，数据包括16线激光雷达、IMU和GPS数据。表1为各算法的均方根误差对比。本文算法表示完整的GPS-激光-IMU融合建图算法。为了验证GPS融合和重力优化对算法精度的提升，分别关闭GPS融合和重力优化功能进行对比试验。本文算法-NoGrav为关闭重力优化功能的建图算法，本文算法-NoGPS为关闭GPS融合功能的建图算法。本文算法与本文算法-NoGrav相比，均方根误差有所降低，说明本文提出的重力优化可以提高建图精度。本文算法与本文算法-NoGPS、FAST-LIO2和LeGO-LOAM相比，精度有大幅度提升，证明了本文算法的有效性。由于FAST-LIO2在初始化部分出现问题，所以误差相对较大。

表1 不同算法的均方根误差Table 1 RMSE of different algorithms m

LIO-SAM-GPS表示融合GPS数据的LIO-SAM算法，本文算法的平移均方根误差仅为LIO-SAMGPS的46%。图6（a）和6（b）分别为本文算法和LIOSAM-GPS误差曲线，其中APE为绝对位姿误差，RMSE为均方根误差，Median为误差中位数，Mean为误差平均数，STD为标准差。这些评估标准下，本文算法均优于LIO-SAM-GPS。

图6 绝对位姿误差曲线Fig.6 Curves of absolute pose error

为了验证本文算法在无法获取GPS信号时的精度，本节进一步设计了在不融合GPS数据时各算法的精度对比试验。采用M2DGR数据集［24］，该数据集中录制了视觉传感器数据、激光点云、IMU和GPS数据，本节实验使用M2DGR的Street_03和Street_08序列。表2和表3分别为各算法的均方根误差与最大平移误差。通过对比可以发现，本文算法在不融合GPS数据时与开源算法的精度接近，保证了算法在GPS拒止场景下的鲁棒性。

表2 不融合GPS数据时的均方根误差Table 2 RMSE when GPS data is not fused m

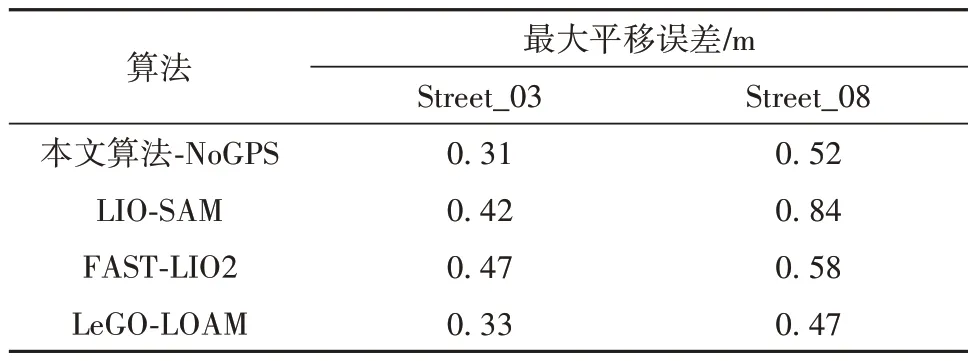
表3 不融合GPS数据时的最大平移误差Table 3 Maximum translation error when GPS is not fused m

3.2 大尺度场景下建图结果对比

图7中红线为移动平台的行驶轨迹，轨迹全长超过6 km，由于硬件平台速度的限制，行驶时间约1.5 h。为了测试算法在大尺度场景下的建图与定位精度，本文在如图8所示场景下进行了对比试验。图8展示了本文算法在该场景下的建图结果。为了能够与其他开源算法进行充分对比，本文中分别从定性和定量两个角度对实验结果进行分析。

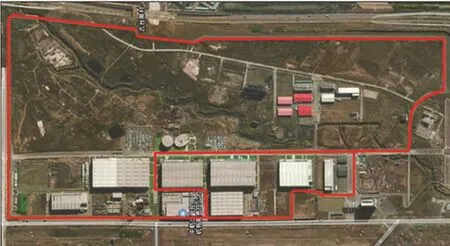
图7 小车行驶轨迹Fig.7 Traveling path of the vehicle

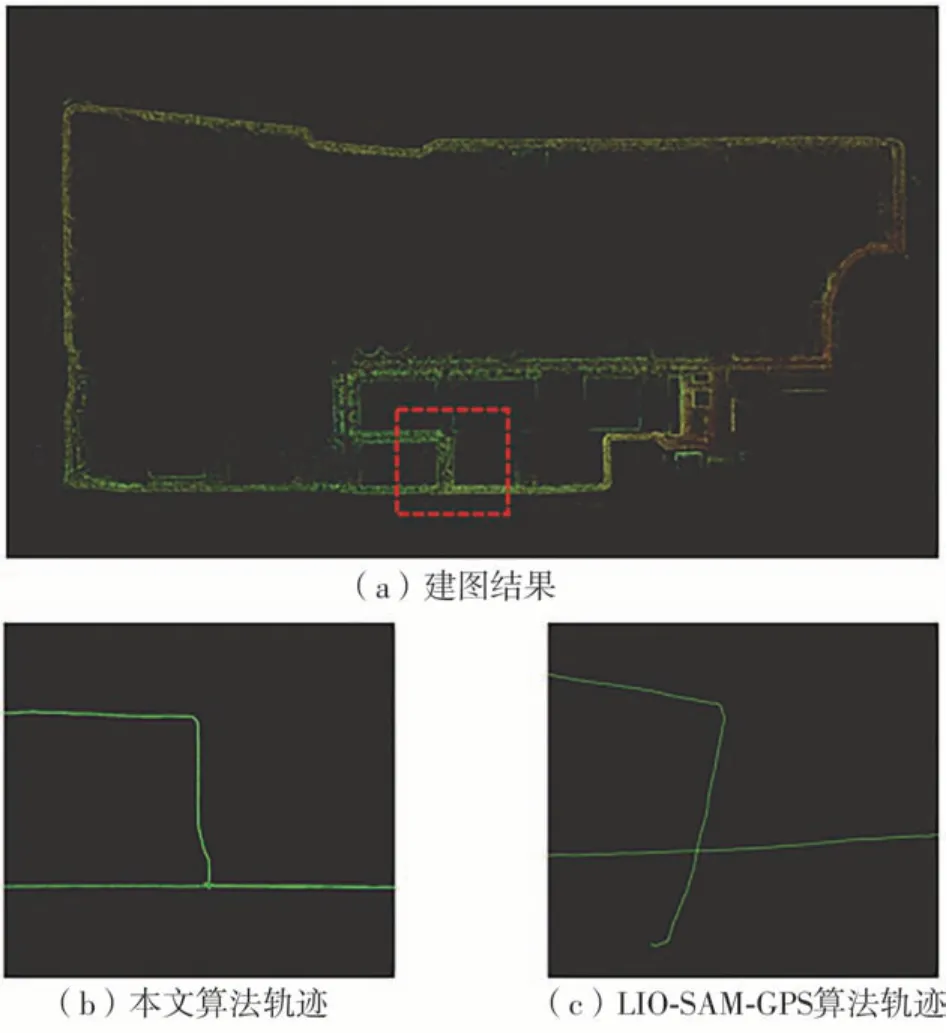
图8 大尺度场景建图结果Fig.8 Mapping result of large-scale environment

在不融合GPS的情况下，本文算法-NoGPS、FAST-LIO2和LeGO-LOAM在空旷的场景中由于点云数量不足均无法完成建图任务，因此不对建图效果进行对比。从定性角度分析，图8（a）图表示建图结果，图8（b）中轨迹表示本文算法未构成回环约束时在虚框处的轨迹，图8（c）中轨迹表示LIO-SAMGPS未构成回环约束时在虚框处的轨迹，在该处小车的轨迹形成了一个回环，可以明显看出在未构成回环约束之前本文算法的轨迹一致性较好而LIOSAM-GPS发生了严重的偏差。从定量角度分析，如表4所示，当回到出发点时本文算法的起始误差为0.11 m，精度高于LIO-SAM-GPS。

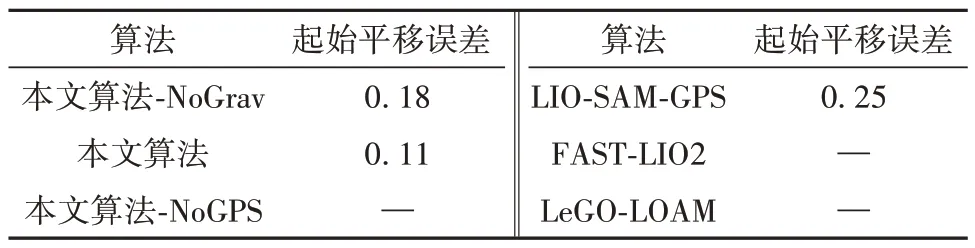
表4 起始平移误差Table 4 End-to-end translation error m

由于该场景中的部分区域非常空旷导致点云数量不足，因此机器人运动到该区域时会出现相邻帧匹配失败的问题。而且由于后端无法构建有效的约束，当回到出发点时，已经无法通过回环优化修正累计误差。因此没有融合GPS数据的情况下，无法建立有效可用的地图。GPS数据可以提供机器人的绝对位置信息，能够及时修正误差，因此融合GPS数据可以提高系统鲁棒性，能够防止里程计漂移的问题。

4 结论

本文提出了一种基于迭代卡尔曼滤波器的GPS-激光-IMU融合建图算法，解决了室外大尺度场景下误差累积的问题，提高了特征稀疏场景下的鲁棒性，能够应用在空旷的室外环境中。本文将重力的优化转换为旋转矩阵群上的问题，避免了重力过参数化和协方差矩阵奇异性的问题。实验表明，本文算法的均方根误差为0.089 m，与其他算法相比本文算法达到了更高的精度。后续将研究在GPS拒止场景下如何降低误差累积对定位和建图的影响。