提升新能源短时性功率冲击下暂态频率安全的储能紧急控制策略

魏玖明，李兆伟2，，李碧君，吴雪莲，朱 玲，赖业宁

（1.南瑞集团有限公司（国网电力科学研究院有限公司），江苏省南京市 211106；2.华北电力大学电气与电子工程学院，北京市 102206）

0 引言

根据《2030 年前碳达峰行动方案》［1］，“构建新能源占比逐渐提高的新型电力系统”是支撑国家能源转型与“双碳”战略实施的关键举措。新型电力系统中的高比例新能源大量置换常规电源，造成电网转动惯量、调频能力下降［2-4］，暂态频率安全已经成为制约新型电力系统发展的瓶颈问题。近年来，国内外已发生多起大频差扰动事件［5-7］。

对于新能源占比不断提高的新型电力系统，引发低频问题的不仅有新能源脱网或直流闭锁等带来永久性功率扰动的故障，短路故障引起大规模新能源低电压穿越（以下简称“低穿”）等带来的短时性功率冲击也会导致系统频率快速变化［8］，甚至跌破第三道防线频率阈值。文献［9］在对欧洲某电网最大非同步电源渗透率的研究中指出，电网故障引起的风电机组低穿对频率的影响可能比大机组跳闸更严重。文献［10］指出，中国东北电网存在单一电网故障引起大面积新能源进入低穿的风险，严重情况下超过90% 的新能源进入低穿，短时扰动功率超过20 GW，占总负荷40%以上，威胁电网频率安全。

目前，已经有大量文献［11-13］对新能源的低穿能力、低穿特性以及低穿控制策略展开研究，如双馈风机有着机械载荷作为约束，其在低穿恢复期间有功功率不能快速恢复［14］；在暂态稳定问题较为突出的风火打捆送端电网，新能源低穿恢复期间较慢的有功功率恢复速度有利于电网的功角稳定［15］。然而，对于大规模新能源低穿引起的暂态频率安全问题目前还缺少解决方案。

紧急控制作为电力系统稳定控制的第二道防线，是针对预先考虑的故障形式和运行方式，由故障事件触发预定的控制策略，如切机、切负荷等措施［16］。由于不需要系统频率等反馈信号触发，可以在监测到故障后的百毫秒尺度快速动作，统筹全网可用资源，使得系统在严重故障后快速达到新的平衡状态，但传统的控制资源仅支持单向控制，应对大规模新能源短时性功率冲击容易引起连锁高频事件。

电化学储能（以下简称储能）作为新型电能存储的重要方式，具有响应速度快、功率双向可调等优点，使得储能在配合集中/分布式新能源并网、电网运行辅助等方面具有不可替代的地位［17-18］。与传统的切机、切负荷等离散、单向控制资源相比，非常适用于短时性功率扰动后的紧急控制［19-20］。近年来，国家和地方相继出台了系列政策，很多新能源场站按装机容量的10%～20%配置储能［21-22］，如此巨量的资源为储能紧急控制创造了良好的条件。

本文首先分析了新型电力系统中大面积新能源低穿产生的短时性功率冲击对系统频率的影响。通过建立简化的系统频率响应模型，得到了新能源短时性功率冲击下计及储能紧急功率控制的系统频率响应时域表达式，通过该时域表达式总结归纳了储能释放功率和持续时间对系统频率特性的影响。并以此为理论依据，提出了避免低频减载动作的最小储能紧急释放能量计算方法，并给出满足要求的储能紧急控制功率和持续时间策略。最后，在IEEE 10 机39 节点系统进行仿真分析，验证了所提储能功率紧急控制策略的有效性。

1 新能源低穿影响下的系统频率响应特性

目前，已有较多文献对新能源机组的低穿过程和功率控制模式进行了研究和论述。国家标准《风电场接入电力系统技术规定》［23］和《光伏发电站接入电力系统技术规定》［24］中对风电和光伏的低穿基本要求、有功功率恢复速率、动态无功支撑能力做出了相应规定。以风电机组为例，在电网故障期间没有切出的风电机组，其有功功率在故障清除后应快速恢复，以至少每秒20%额定功率的速率恢复至故障前的值。

整个过程中风电机组有功出力与机端电压的时序曲线如图1 所示。

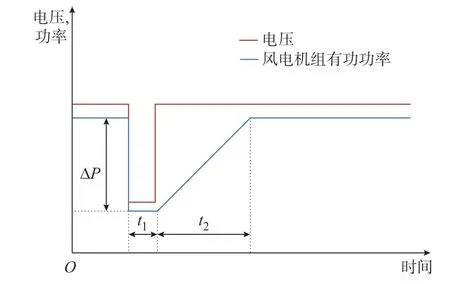
图1 低穿过程示意图Fig.1 Schematic diagram of low voltage ride-through process

风电、光伏等新能源大规模并网，致使同步机组被逐步替代。若新能源大规模并网后除同步机组外其他惯性支撑资源不参与电力系统惯量响应，则此时的系统等效惯性常数将逐渐下降，表达式［25］为：

式中：Hequ为等效惯性时间常数；Hg为并网同步机组惯性时间常数；SG为并网同步机组额定容量；SRES为并网新能源机组额定容量；N为系统中并网的同步机组数量。

综合分析图1 及式（1），大规模新能源低穿带来的有功冲击量大，持续时间一般在1～3 s。该时间尺度内常规发电机的一次调频响应较少，按现有国家标准要求的新能源一次调频响应速度，新能源一次调频响应也较小（进入低穿及恢复过程中的新能源无法提供一次调频和虚拟惯量响应）［26］。因此，对低穿过程中系统频率跌落起主要抑制作用的是系统惯量。由式（1）可以看出，随着系统中新能源占比的不断提高，系统的等效惯量水平逐步降低。低惯量系统中新能源低穿短时性功率冲击下系统频率偏差幅度增大，跌落速度更快。若跌破低频减载的动作阈值，还会导致后续高频事件发生，高低频连锁反应下极易引发全网停电事故，严重威胁电网频率安全。

2 考虑储能参与紧急功率控制的系统频率响应模型

为了对系统的频率特征进行分析，首先需要建立系统的频率响应模型，如图2 所示。图中：ωref为参考角频率；ΔE为频率误差传递函数；调速器以纯增益1/R简化表示；ΔPm为同步机机械功率；ΔP为扰动功率；ΔPe为同步机电磁功率；M为与转动惯量相关的转子时间常数；L为负荷的有功频率响应系数；s为拉普拉斯算子；Δω为系统响应角频率。

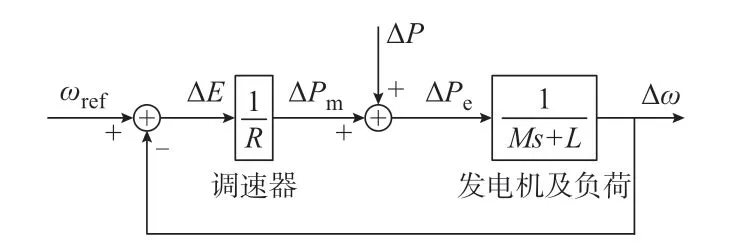
图2 同步机组发电系统的简化聚合频率模型Fig.2 Simplified aggregate frequency model of synchronous unit generation system

由于新型电力系统惯量较小，在受到短时性功率冲击后系统频率快速到达最低点，而同步发电机一次调频响应具有滞后性，在频率快速下降阶段还未来得及动作，对这部分频率变化影响较小，而对频率恢复阶段的影响较为明显［10］。因此，为简化分析短时性功率冲击对系统频率最低点的影响，忽略同步机的调速器作用，设扰动功率为ΔP，则系统的频率响应可以表示为：

式中：Δω(s)为系统频率响应函数；ΔG(s)为系统的频率-有功功率传递函数。

为了不影响结论的一般性，简化分析新能源低穿期间产生的短时性冲击功率以及储能电站所释放的紧急控制功率相叠加后系统的频率响应特性。考虑故障后电压瞬时恢复至0.9 p.u.以上，新能源有功功率按照固定斜率缓慢恢复，储能电站在故障消失后考虑一定延时，按照既定的紧急控制策略释放有功功率，为最大化发挥储能的紧急控制效果，同时避免新能源低穿后系统出现高频，延时后储能功率采用方波形式输出。相关曲线如图3 所示。

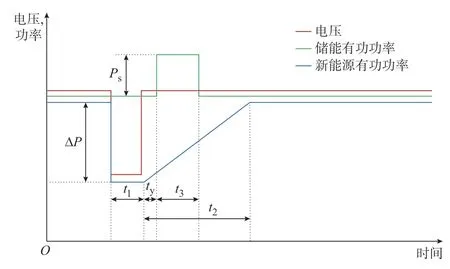
图3 理想电压恢复曲线、新能源有功功率曲线和储能功率曲线Fig.3 Ideal voltage recovery curve, active power curve of renewable energy and energy storage power curve

虽然电压跌落会直接影响负荷功率，但基于网络平衡，忽略负荷的影响可以得到较为保守的低频问题分析结论。因此，为了简化分析，忽略暂态过程中负荷的影响，使非阶跃功率扰动量仅由新能源低穿期间的短时性冲击功率和储能紧急控制功率构成，扰动量对应的频域表达式为：

式中：P为新能源低穿期间产生的短时性冲击功率；Ps为储能释放的有功功率；ty为紧急控制启动延时时间；t1为新能源低穿持续时间；t2为新能源低穿恢复时间；t3为储能释放持续时间。

将式（4）代入式（2）中，得到系统的频率响应模型如下：

通过拉普拉斯反变换得到此时系统频率对应的时域表达式如式（6）所示，其中，ε（·）表示单位阶跃函数。

3 储能释放功率和持续时间对短时性功率冲击下系统频率响应的影响分析

由式（6）可知，短时性功率冲击下考虑储能紧急功率控制，系统的频率特性不仅与新能源低穿产生的短时性冲击功率P、紧急控制启动延时时间ty、低穿持续时间t1、低穿恢复时间t2有关，还与储能的释放功率Ps以及储能的释放持续时间t3有关。本章以t3≤t2为前提（t3＞t2容易引起系统高频事件），讨论储能的紧急控制策略，即释放功率Ps以及释放持续时间t3对系统频率特性的影响。

3.1 短时性功率扰动下考虑储能紧急控制策略的系统暂态频率分段特性

已知系统的频率响应式（6）是与t相关的阶跃函数，故可以将式（6）改写为与t相关的分段函数。以50 Hz 作为正常运行工况下的频率，得到系统的频率响应表达式如式（7）所示。鉴于系统的频率变化率和频率响应表达式的二阶导数可以对系统频率的响应过程进行更详细的分析，故在开区间内对式（7）进行求导，公式推导过程详见附录A。对务阶段分段函数的表达式进行分析，过程如下。

3.1.1 0≤t＜t1+ty阶段

在0 时刻，系统发生故障，新能源进入低穿模式，系统中产生功率缺额，导致系统频率开始跌落；在t1时刻故障切除，系统电压恢复，新能源进入低穿恢复模式，此时缺额功率开始逐渐恢复，频率跌落速度逐渐趋缓。由于储能电站是在主站检测到故障信号后经过ty的延时后才会开始工作，故系统此时的不平衡功率主要与新能源低穿产生的缺额功率有关。

虽然储能的启动存在一定的延时，但是储能参与紧急控制的目的是在系统频率到达最低点之前就释放有功功率，进而达到提升频率最低点的效果。因此，ty需满足如式（8）所示约束才能改善系统最低频率。

式中：k=-L/M。

在该阶段中，系统频率持续跌落，但跌落速度逐渐趋缓。

3.1.2t1+ty≤t＜t1+ty+t3阶 段

在t1+ty时刻，储能开始投入工作，新能源处于低穿恢复过程。结合附录A 式（A1）中储能释放功率和释放持续时间对系统频率变化率的影响，可以分成以下2 种情况：

1） 当Ps满 足 关 系 式Ps≥Pek(t1+ty)+P(ek(t1+ty-t)-ekty)/(kt2)时，系统频率变化率恒大于0，即储能紧急控制功率较大时，施加后瞬间系统频率由下降转为恢复上升。此时，系统频率会出现一个极小值点，该极小值点出现的时刻和取值公式如下：

2）当Ps满 足 关 系 式Ps＜Pek(t1+ty)+P(1-ekty)/(kt2)时，在t1+ty时刻，系统频率变化率小于0，即储能紧急控制功率较小，施加后瞬间系统频率仍在跌落，但在储能工作期间是否会使系统频率由下降转为恢复上升仍需讨论。结合附录A 式（A2）中储能释放功率和释放持续时间对系统频率二阶导数的影响，可以继续分成以下2 种情况：

a）当Ps和t3满 足 关 系 式Psekt3-Pek(t1+ty+t3)-P(1-ek(ty+t3))/(kt2)≤0 时，系统频率变化率恒小于0，系统频率继续跌落，即储能紧急控制量过小，控制结束后仍无法让系统频率由下降转为恢复上升。

b）当Ps和t3满足关系式Psekt3-Pek(t1+ty+t3)-P(1-ek(ty+t3))/(kt2)＞0 时，系统频率变化率单调递增过零点，即储能紧急控制量可以使系统频率在储能工作期间先跌落后恢复上升。此时，会出现一个极小值点，该极小值点出现的时刻和取值公式如下：

3.1.3t1+ty+t3≤t＜t1+t2阶 段

在t1+ty+t3时刻，储能退出工作，此时新能源仍处于低穿恢复阶段，系统必然存在缺额功率，使系统频率下降，即

结合附录A 式（A1）中储能释放功率和释放持续时间对系统频率变化率的影响，以及式（A2）中对系统频率二阶导数的影响，分为以下2 种情况：

1）当Ps和t3满 足 关 系 式Ps(ek(t2-ty)-ek(t2-ty-t3))-Pek(t1+t2)-P(1-ekt2)/(kt2)≤0 时，系统频率变化率单调递增且恒小于0，系统频率持续跌落。由式（7）可知，系统频率最终会趋于50 Hz，则该种情况说明储能紧急控制量过大，在储能工作期间出现频率超调的情况，使系统频率在储能退出后缓慢跌落，在该阶段不存在频率极小值的情况。

2）当Ps和t3满 足 关 系 式Ps(ek(t2-ty)-ek(t2-ty-t3))-Pek(t1+t2)-P(1-ekt2)/(kt2)＞0 时，系统频率变化率单调递增过零点，即储能紧急控制量不足使得系统频率出现二次跌落，并在系统惯量和阻尼的作用下缓慢恢复。此时，会出现一个极小值点，该极小值点出现的时刻和取值公式如下：

3.2 不同储能紧急控制策略下系统暂态频率的全过程特性

根据3.1 节分析得到务阶段不同储能释放功率和持续时间对系统频率特性的影响后，可以将务阶段的不同情况进行组合，得到完整的频率特性变化曲线，详细的组合过程见附录B。

虽然不同阶段的频率变化情况不同，但整体可以分为以下3 类：

1）储能紧急控制量过小，在储能工作期间系统频率不存在超调现象，频率响应曲线有且只有一个极小值点，出现时间和取值由式（13）和式（14）进行求解，参考曲线如图4（a）所示。

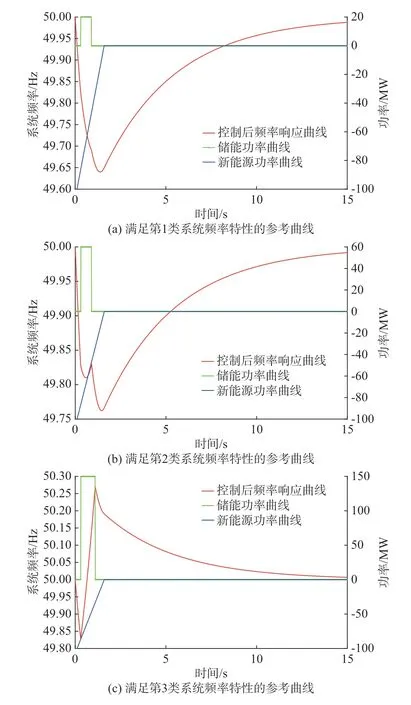
图4 以t3＜t2为前提的不同Ps和t3对系统频率特性曲线的影响Fig.4 Effect of different Ps and t3 on system frequency characteristic curves with assumption of t3＜t2

2）储能紧急控制量适量，在储能工作期间系统频率先跌落后恢复上升，在储能退出后系统频率出现二次跌落，并在系统惯量和阻尼的作用下缓慢恢复，此时系统频率响应曲线存在2 个极小值点。储能紧急控制量不同，第1 个极小值点出现的时间和取值也有差异，求解公式为式（9）、式（10）或式（11）、式（12），第2 个极小值点出现的时间和取值由式（13）、式（14）进行求解，参考曲线如图4（b）所示。

3）储能紧急控制量过大，储能工作期间系统频率出现超调现象，此时系统频率响应曲线有且只有一个极小值点。储能紧急控制量不同，该极小值点出现的时间和取值也有差异，求解公式为式（9）、式（10）或式（11）、式（12），参考曲线如图4（c）所示。

综上分析可知，短时性功率扰动下对储能紧急功率控制的精度要求高，既需要快速释放足够的能量避免暂态频率越过低频减载阈值，也需要避免释放过多能量，引起连锁高频事件，储能紧急控制功率的退出时机也非常重要。

4 储能紧急功率控制策略的制定

短时性功率扰动下储能紧急功率控制不仅需要避免暂态频率越过低频减载阈值，同时也需要避免因释放过多能量而引起频率超调。首先，需要根据式（7）制定避免系统高频的约束条件，即f(t)≤50 Hz。

同时，由第3 章的分析可以得出，在f(t)≤50 Hz 时，系统的频率特性存在以下2 种可能：

1）储能紧急控制量过小，在储能工作期间系统频率不存在超调现象，频率响应曲线有且只有一个极小值点，取值由式（14）进行求解。

2）储能紧急控制量适量，在储能工作期间系统频率先跌落后恢复上升，在储能退出后系统频率出现二次跌落，并在系统惯量和阻尼的作用下缓慢恢复。此时，系统频率响应曲线存在2 个极小值点，第1 个极小值点的取值由式（10）或式（12）进行求解，第2 个极小值点的取值由式（14）进行求解。

避免因短时性功率冲击而导致系统频率跌破低频减载阈值是将储能纳入紧急功率控制的目标之一，可以设定一个阈值flimit，使系统的频率最低点不小于该值作为一种约束条件。

最后，可以将最小的储能释放能量C作为控制策略制定的目标函数，计算公式为Pst3。将其作为目标函数进行求解，可以得到系统在受到短时性功率冲击后，为避免触发低频减载阈值，储能装置所需要释放的最小能量，同时也是储能装置能否有效运行的判断依据。

综上所述，该单目标优化问题可以描述为以下2 种：

式中：PsN为储能的额定功率。

式（15）表示的是系统频率响应曲线出现2 个极小值点时，为达成避免触发低频减载阈值这一目标所需要的最小储能释放能量，以及对应的储能释放功率和释放持续时间；式（16）表示的是系统频率响应曲线出现1 个极小值点时，为达成避免触发低频减载阈值这一目标所需要的最小储能释放能量，以及对应的储能释放功率和释放持续时间。可以通过这2 个优化函数的求解结果，以最优解是否存在以及最优解的大小来决定采取何种方案。

由于短时性功率扰动对储能紧急控制策略要求非常精准，传统基于离线保守方式制定紧急控制策略的模式非常容易引起储能控制量过大而带来连锁高频问题，且实际仿真发现，短路故障引起大规模新能源低穿的保守方式极难确定。因此，本文所提出的方法主要适用于在线分析故障特性进行预决策［27］。首先，通过在线跟踪系统工况，得到务新能源机组的运行状态和运行特性。其次，基于在线数据，通过对预想故障下的系统特性进行仿真，获取不同新能源场站在低穿期间的有功曲线，即获得不同新能源场站的短时性冲击功率P、低穿持续时间t1和低穿恢复时间t2。对于不同的新能源低穿策略下有功曲线的差异，可以通过分段修正方法进行等值［28］，考虑穿越期间的能量冲击不变，得到系统等效短时性功率曲线，以该曲线的信息来初步制定一种储能紧急控制策略，并在此基础上进行迭代修正，优化并提高策略的控制效果。最后，在线刷新相应的稳定控制系统在线策略表，在电网发生故障时由稳定控制主站下达控制指令，匹配在线策略表保证系统安全稳定。其中，策略的制定流程见图5。

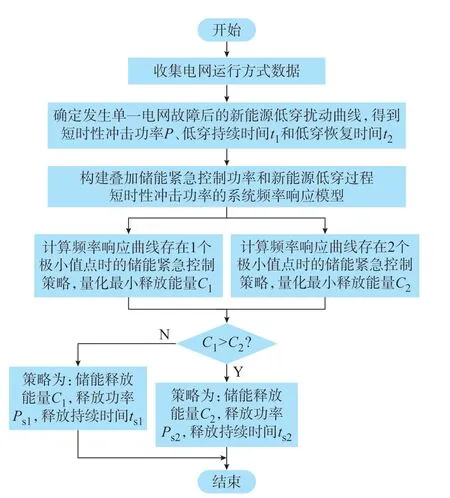
图5 储能紧急功率控制策略的制定流程Fig.5 Formulation process of power emergency control strategies using energy storage

详细的控制步骤如下：

1）收集电网运行数据，通过在线跟踪系统工况，确定系统的等效惯性时间常数［4］以及务新能源机组的运行状态和运行特性；

2）基于在线数据仿真获得短路故障后所有进入低穿的新能源功率曲线，保持冲击能量不变，基于分段修正方法对新能源进行等值，得到系统等效短时性冲击功率P、低穿持续时间t1和低穿恢复时间t2；

3）分别计算频率响应曲线中存在1 个极小值点和2 个极小值点时的储能释放能量和释放策略，并选择最小的储能释放能量作为控制策略。

5 算例验证

以IEEE 10 机39 节点系统网络结构为例，运行条件为：总负荷为1 000 MW，采用恒功率模型，负荷的有功频率响应系数L=2.0；含同步机7 台，惯性时间常数Hg为4 s，风电场站3 座，额定容量分别为100、50、50 MW，系统详细参数和结构图见附录C。

短路故障发生在节点2 和节点3 之间，接地阻抗为0，在故障发生0.1 s 后进行切除。为了便于计算，风电机组低穿期间采用指定功率控制，功率控制值为0，恢复初始值按照低穿期间实际功率控制。《风电场接入电力系统技术规定》［23］中要求对于风电低穿恢复期间有功功率恢复速率以至少每秒20%额定功率的速率恢复，可以设定新能源的低穿持续时间t1为0.1 s，低穿恢复时间t2为1.5 s。暂态稳定紧急控制对控制速度有较高的要求，若控制措施执行时间过长会导致系统无法恢复暂态稳定或需要较大控制代价才能恢复稳定，一般从故障发生到控制措施实施的时间不应超过300 ms［29］。因此，可将该仿真算例中紧急控制启动延时时间ty设定为200 ms，且由式（8）计算可得，200 ms 小于1.25 s，符合约束条件。假设在故障发生后所有新能源均进入低穿模式，且没有新能源脱网。为了给其他控制装置留有一定裕度，可以要求系统承受的最低频率不低于49.4 Hz。

通过模拟储能参与紧急功率控制后，对受到短时性功率冲击的系统频率最低点的控制效果，来验证储能临界释放功率和临界释放持续时间的准确性。

根据第4 章制定的储能紧急功率控制策略，求解结果如表1 所示。

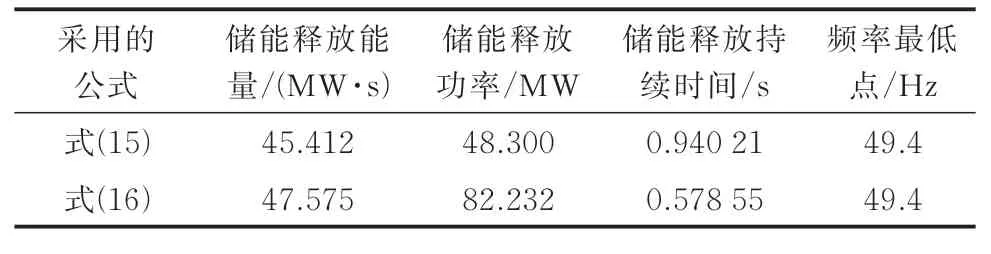
表1 储能紧急功率控制策略计算结果Table 1 Calculation results of power emergency control strategy using energy storage

对策略中得到的为避免触发低频减载阈值的最小储能释放能量进行验证。将储能可释放的能量限定在不超过45.412 MW·s，改变储能的释放功率，得到对应的储能释放持续时间，并要求储能释放持续时间t3小于新能源低穿恢复时间t2。以这种方式形成不同储能释放策略，验证结果如图6（a）所示。可以看出，当储能释放能量小于45.412 MW·s 且储能释放持续时间t3小于新能源低穿恢复时间t2时，无论采取何种储能释放策略，都无法使系统最大频率偏差小于-0.6 Hz。

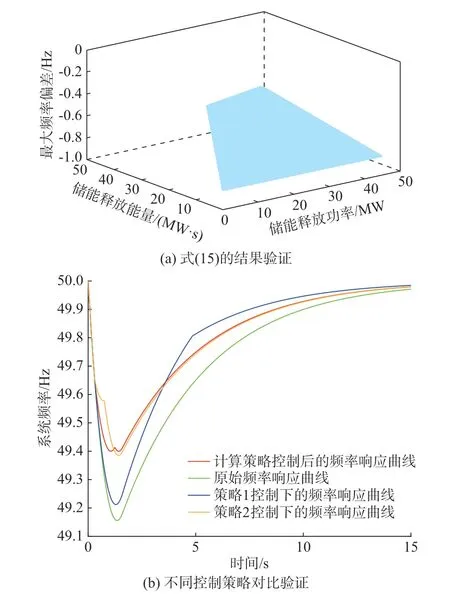
图6 储能紧急功率控制策略的验证结果Fig.6 Validation results of power emergency control strategy using energy storage

同时，将储能释放能量固定在45.412 MW·s，截取部分储能释放策略（策略1 和2）与计算得到的储能释放策略进行对比。可以看出，只有计算得到的储能释放策略可以将系统频率最低点控制在49.4 Hz，结果如图6（b）所示。

综上所述，基于这2 种单目标优化问题所制定的策略在理论上是可行的，且可以量化得到最小储能释放能量。

通过理论模型的计算，得到系统频率响应曲线如图7（a）所示，再通过IEEE 10 机39 节点系统进行仿真对比，得到系统的频率响应曲线如图7（b）所示。

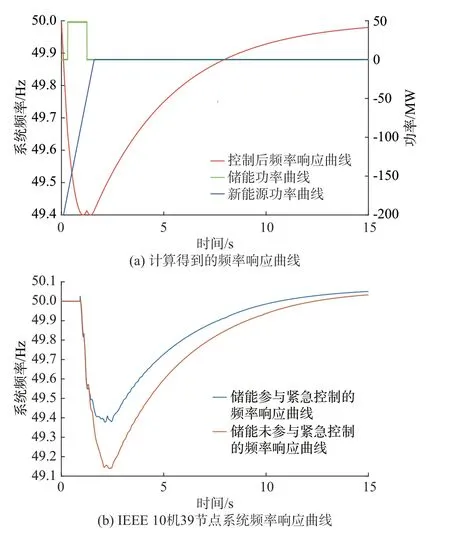
图7 理论曲线与仿真曲线对比Fig.7 Comparison of theoretical and simulation curves

结果表明，仿真得到的频率特性与计算得到的频率特性相同，且满足在留有一定裕度的情况下避免触发低频减载阈值的要求，与储能未参与紧急控制的频率响应曲线相比，系统频率最低点得到了有效提升。

6 结语

新型电力系统中的高比例新能源大量替代常规电源，导致系统的惯量水平和频率调节能力下降，单一短路故障容易引起大规模新能源进入低穿，对电网产生短时性功率冲击，使频率快速突破低频减载阈值，进而引发高低频连锁故障，威胁电网频率安全。针对这一问题，本文提出利用储能进行紧急功率控制的方案，主要研究结论如下：

1）提出了新能源短时性功率冲击下计及储能紧急功率控制的系统频率响应分析模型，以此为基础分析了短时性功率扰动下考虑储能紧急控制策略的系统暂态频率分段特征，在储能释放持续时间小于新能源低穿恢复时间时，总结了不同储能紧急控制策略下系统暂态频率的全过程特性。短时性功率扰动下对紧急控制策略的精准性要求更高：当储能控制量过小，其对短时性功率扰动下的暂态频率改善较小，系统频率响应曲线只存在一个极小值点；当储能控制量适量时，频率响应曲线存在二次跌落，有2 个极小值点；储能控制量过大，频率可能出现超调现象，需要重点关注暂态高频风险带来的连锁反应。

2）提出了避免新能源低穿导致低频减载动作的最小储能释放能量评估方法，当储能释放能量小于该值，仅利用储能紧急控制无法避免系统暂态频率跌破低频减载阈值，需要考虑与其他资源协调配合。基于本文所提出的储能脉冲型紧急控制策略，可以有效提高短时性功率冲击下系统的暂态频率安全水平。

目前研究的紧急控制策略基于在线分析故障特性进行预决策，后续将结合新能源低穿状态的实时掌握信息，并通过细化监测的信息，建立监测信息与新能源缺额功率和低穿恢复时间之间的联系，开展基于实时缺额功率判别的紧急控制策略研究。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。