计及频率响应时空相关性的新能源电力系统惯量估计方法

裴 铭，叶 林，罗雅迪，沙立成，张再驰，宋旭日

（1.中国农业大学信息与电气工程学院，北京市 100083；2.中国电力科学研究院有限公司，北京市 100192；3.国网北京市电力公司，北京市 100031；4.国网北京市电力公司电力科学研究院，北京市 100075）

0 引言

随着风电、光伏等大规模新能源的并网，电力系统呈现高比例新能源接入与高比例电力电子设备应用的“双高”特性。然而，采用电力电子接口并网的新能源为电力系统所提供的惯量，被称为“虚拟惯量”［1］，无法像火电、水电等同步发电机组一样为系统提供可靠的一次调频支撑［2］。此外，功率扰动下系统频率变化率（rate of change of frequency，RoCoF）和频率最低点显著恶化，从而导致大规模停电等极端事故的发生［3-4］。为确保高比例新能源电力系统的安全稳定运行，有效的惯量估计成为预判电力系统频率失稳的重要手段［5］。

由于风电、光伏等新能源发电的随机性和时变性，新能源发电节点的惯性响应过程具有不确定性，对系统安全稳定运行具有关键性影响。因此，对新能源发电节点及新型电力系统的惯量进行及时跟踪计算十分有必要［6］。文献［7］基于同步相量测量单元（phasor measurement unit，PMU），提出了利用扰动后频率测量数据计算系统等效惯量的方法。文献［8］基于定义的中心频率平方偏差，提出了新能源电力系统等效惯量的计算方法。文献［9］利用惯性常数-频率状态摆动方程，对不同种类的新能源发电机组惯量进行等效计算。综上所述，利用频率观测值实时计算电力系统的惯量是可行的技术方案，可为电力系统惯量的实时估计提供数据支撑和理论基础。

在电力系统惯量实时估计方法中，国内外研究常使用数据采集与监控（supervisory control and data acquisition，SCADA）系统或PMU 的实时测量信息作为输入，利用时序模型［10］、拉普拉斯模型［11］或模态模型［12］对系统惯量进行实时估计。近年来，借助状态空间建模的思想，文献［13］从模型驱动的角度解析电力系统频率响应对系统惯量的作用机理，通过输入实时更新的测量数据，完成系统惯量的实时估计。文献［14］基于系统节点频率测量信息构建状态空间模型，利用无迹卡尔曼滤波（unscented Kalman filter，UKF）来估计系统惯量；文献［15］利用容积卡尔曼滤波器，通过构造以节点频率测量值和频率估计值之间误差最小化的目标函数，建立系统频率的评估模型。然而，在新能源电力系统的实际应用中，基于状态空间建模的滤波器往往存在收敛慢的问题［16］，在初始估计结果的基础上引入平滑器，可以使状态估计值快速收敛［17］。此外，新能源电力系统频率具有不确定性强、波动性大的特点，会影响系统惯量的准确估计［18］。上述研究仅利用自身节点频率或惯性中心频率的观测值，难以精准感知整个新能源电力系统惯量的变化趋势。

事实上，对于一个多节点的新能源电力系统，当一个节点的频率发生变化时，会通过输电线路和变压器等设备传播到其他节点，导致系统内其他节点的频率随之发生变化，这种频率传递和响应过程使节点之间的频率响应形成强耦合的相关性［19］。因此，分析系统频率的响应过程，进而充分挖掘节点频率响应之间的相关性，可为系统惯量的估计提供充分的数据支撑［20］。其中，文献［21］根据频率测量装置在电力系统内的安装位置不同，基于最小二乘拟合算法，量化系统内不同节点频率之间的空间相关性；文献［22］通过构建皮尔逊相关系数矩阵来衡量动态时刻下系统内务节点频率的相关性。然而，上述相关性分析算法只是量化不同时间序列间点对点的相关程度，但是对于电力系统频率分析而言，节点之间的频率幅值差异并不明显，上述相关性分析算法不够精细化［23-24］。除此之外，不同估计周期内，务节点频率之间的相关关系差异性大。因此，利用历史观测信息所得出的点对点的相关性结论，并不能有效支撑未来时刻节点间频率相关程度的分析。而因果相关分析算法的实质就是从概率统计的角度判断系统内某一节点的频率变化是否会影响目标节点的频率变化［25］，从而可以最大限度地筛选用于惯量估计的有效节点集合。

综上，本文聚焦于计及新能源发电节点的系统惯量估计，并围绕以下问题展开研究：1）如何量化系统内务节点频率响应之间的时空因果相关性；2）如何建立包括新能源、传统电源在内的系统惯性常数-频率状态空间模型；3）如何对新能源电力系统的惯量进行精准、快速的实时估计。基于此，本文的主要研究内容如下：

1）分析新能源电力系统频率响应过程并追溯惯量来源，结合新能源、传统电源发电节点频率响应过程的摇摆方程，构造系统惯性常数-频率状态空间模型。

2）提出基于Granger 因果检验算法的系统节点频率时空相关性动态量化方法，筛选出系统惯量动态估计所需的相关节点频率观测信息，以因果相关节点频率测量信息为观测变量，改进系统惯性常数-频率状态空间模型。

3）引入UKF 和固定滞后平滑器（fixed-lag smoother，FLS），建立电力系统惯量的两阶段状态估计模型，以改进的IEEE 39 节点系统为例，验证了惯量估计结果的收敛速度和精度，校验了方法在不同运行场景的适应性。

1 新能源电力系统惯量估计基本框架

本文分别从新能源电力系统节点频率响应的时空相关性量化、系统惯性常数-频率状态空间构造与改进、滤波-平滑两阶段的惯量估计建模3 个方面来实现高比例新能源电力系统的惯量估计，从发电节点和电力系统两个空间尺度对惯量进行估计，为精准评估从局部节点到全系统的稳定性、电力系统的运行与控制提供决策支撑。本文理论模型框架如图1 所示。

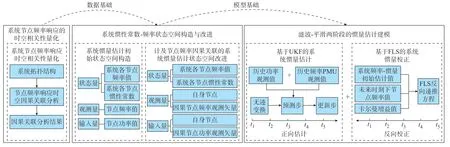
图1 理论模型框架图Fig.1 Framework diagram of theoretical model

本文首先基于Granger 因果检验算法，对电力系统中务节点频率之间的时空因果相关性进行表征，以时空因果相关集合的形式表征务估计周期下节点频率之间的相关性分析结果。基于此，以系统务节点的惯性常数和频率为状态量、以时空因果相关的系统节点频率测量矢量为观测量、以因果相关节点功率测量矢量为输入量，构建计及节点频率因果相关的电力系统状态空间模型。在状态空间的基础上，基于UKF 构造电力系统惯量初始估计模型，进一步结合系统节点频率在超前时刻下的观测值，建立基于FLS 的系统惯量的状态修正模型，使系统估计结果更接近实际值。

2 新能源电力系统惯量估计理论基础

2.1 电力系统惯性响应过程

电力系统惯量是指电力系统在短时间内承受负荷变化时，系统内部机械能的变化量。在电力系统中，惯量是一个非常重要的概念，其直接影响电力系统的稳定性和可靠性［26-28］。本文采用惯性常数H来衡量电力系统的惯量水平，结合摇摆方程来表征新能源电力系统的惯性响应过程。

式中：Hi为发电节点i的惯性常数；Δfi为节点i的频率变化量；ΔPm，i为节点i的机械功率变化量；ΔPe，i为节点i的电磁功率变化量；Di为节点i的负荷频率调节系数；t为时间。

对于同步发电机而言，惯量是惯性大小的量值，可以从转动惯量、动能、惯性常数等不同角度衡量惯性大小；对于新能源发电机组而言，其惯量形式复杂多样，取决于控制方式与机组运行工况。本文从能量的角度出发，利用惯性常数来衡量同步发电机、新能源机组的惯量大小，可以为高比例新能源电力系统的惯量表征提供统一的量化标准。

2.2 高比例新能源电力系统惯量定义与计算

2.2.1 惯量的定义

分析电力系统频率动态响应过程可知，传统电力系统的惯量主要是以火电、水电等常规电源为主的同步机组所提供的转动惯量。但是，新能源发电系统中，风力发电机组具有一定的惯量，光伏发电系统由于没有旋转电机，又被称为零惯量系统。新能源电力系统的总惯量Hsys表示如下：

式中：上标mom、re 分别为同步发电节点、新能源发电节点的对应变量；Hmomi、分别为同步发电节点、新能源发电节点i的惯性常数，分别用于量化同步机转动惯量水平、新能源机组向系统提供的惯量水平；M、R分别为新能源电力系统中传统同步发电节点、新能源发电节点集合。

2.2.2 转动惯量计算

基于系统惯性响应的摇摆方程如式（1）所示。针对同步发电机组的惯性响应过程，在扰动初期，机组一次调频尚未开始动作，即机械功率变化量ΔPm为0，主要由电磁功率的变化量ΔPe来决定，同步发电机组的转动惯性常数Hmomi满足：

式中：fi为节点i的频率。

2.2.3 风力发电机组的惯量计算

风力发电机组的惯量是指风力发电机组转子在运动过程中所具有的惯性，其是描述风力发电机组转动惯性特性的物理量。因此，风力发电机组的惯性常数Hwind，i可参照同步发电机组惯量表达式进行等效计算，即：

式 中：ΔPwind，i为 风 力 发 电 节 点i有 功 输 出 功 率 的 变化量；fwind，i(t)为t时刻风力发电节点i的频率。

2.2.4 光伏发电机组的惯量计算

光伏发电机组通过检测并网点的频率变化，当机组频率发生扰动时需要通过控制有功功率的变化来完成虚拟惯性响应。具体地，光伏发电机组的惯量-频率状态-有功功率关系式如下：

式中：HPV，i为光伏发电节点i的虚拟惯性常数；ΔPPV，i为光伏发电节点i输出功率的变化量；fPV，i(t)为t时刻光伏发电节点i的频率。由于没有与同步机转子角频率对应的物理量，本文采用机组端口频率替代。可见，该定义和计算方法下的虚拟惯量可以有效表征光伏发电系统的频率响应变化、向系统提供有功功率支撑的能力，同时与同步机惯量的量纲一致，便于新能源电力系统惯量的统一建模。

3 计及节点有功功率-频率时空相关的电力系统惯量的状态空间构造

在电力系统分析中，状态空间模型广泛应用于系统分析、控制和优化，通过对已知的动态行为规律进行量化建模，可以预测电力系统在未来时刻的演化过程。

3.1 电力系统惯性常数-频率状态空间模型

在本文中，根据状态空间的基本原理，构造电力系统节点i的惯性常数-频率状态空间基本方程，定义节点i的惯性常数Hi和频率fi为状态变量x=[Hi，fi]，定义节点i处的有功功率变化量为输入变量u=[ΔPi]。按照同步发电节点、新能源发电节点分类构造系统频率状态方程如式（6）所示。

式中：fi(t)为t时刻发电节点i的频率；ΔPi为节点i有功功率在其稳态基础上的变化量；Pi为节点i有功功率的瞬时值；Pi,0为节点i有功功率的稳态值。

对于惯性常数而言，其在估计的周期范围（秒级）内不随时间变化而变化，是一个常量。因此，本文构建系统惯量的状态方程如式（7）所示。

根据惯性常数-频率状态的状态方程，定义节点i处的频率为观测变量，构造电力系统节点频率的观测方程为：

3.2 考虑频率响应时空相关的状态空间模型

3.2.1 系统节点频率时空相关量化分析

本文引入Granger 因果检验算法量化节点间频率响应过程的时空相关性。因果关系基于统计学中的零假设，其原理是通过判断增加因变量是否有助于预测结果变量，从而检验因变量和结果变量之间的因果相关性［29-30］。如果同时使用频率序列fx和目标频率序列fy的历史观测值的预测效果优于仅使用目标频率序列fy自身历史观测值的预测效果，则将fx称为fy的Granger 因变量或fx是引起fy变化的Granger 原 因［31］。附 录A 图A1 展 示 了Granger 因 果关系应用于系统节点间频率时序的原理。

根据系统内其他节点j与节点i的时空因果相关 判 别 因 子Kct，i，j，针 对 节 点i的 频 率 观 测 值，在 满 足Kct，i，j=1 的 前 提 条 件 下，筛 选 出 在t时 刻 与 节 点i频率具有因果相关性的节点集合G。

式 中：gi，t，nc为t时 刻 与 节 点i具 有 时 空 因 果 相 关 性 的第nc个节点；Nci为与节点i具有时空相关性的节点数量，且随着状态估计周期变化而动态变化。

利用系统务节点频率之间的时空因果相关分析结 果，定 义t时 刻 节 点i的 频 率 状 态 矢 量fS，i，t为：

式 中：fS，i，t为t时 刻 节 点i的 频 率 状 态 矢 量，是 节 点i的 频 率 状 态 值fi，t与 节 点i时 空 相 关 频 率 集 合的并集，维度为1×(Nci+1)。

另 外，定 义fS，g，i为 节 点i的 频 率 状 态 矢 量fS，i，t在集合G中的索引元素。

3.2.2 状态空间模型修正

根据节点频率的时空相关性分析结果，分别对电力系统惯量估计的状态方程和测量方程进行修正。

1）状态方程修正

定义节点i的频率状态矢量fS，i和节点惯性常数Hi为改进状态变量x=［Hi，fS，i］，定义节点i处的所有联络线有功功率变化量ΔPℓ，i组成输入变量矢量u=[ΔPℓ，i]，ℓ ∈Li，构造时空相关的频率状态方程如下：

式中：fS，g，i(t)为t时刻发电节点i的时空相关频率状态 变 量；GS，i，t为 节 点i在t时 刻 的 频 率 相 关 节 点g的集 合；Li为 节 点i的 联 络 线ℓ 的 序 号 集 合。Nci+1 为节点频率状态矢量的维度，在本文中利用时空相关节点与自身节点的惯性常数-频率状态响应均值，从而降低某一节点频率测量误差的影响，从而提升系统惯量的估计精度。

由于系统惯量的状态方程式（6）中不含有频率测量信息，在本文中不做修正。

2）观测方程修正

在状态方程修正的基础上，将节点频率状态矢量定义为观测变量，构造观测方程如下：

式中：fmeasi为节点i的观测变量，包括自身节点的频率测量值fmeasi和其时空相关节点的频率测量值，维度为1×(Nci+1)。

4 考虑频率动态响应的电力系统惯量估计模型

4.1 卡尔曼滤波算法基本原理

卡尔曼滤波（Kalman filter，KF）算法是一种经典的递归滤波器，利用当前时刻的状态估计和观测数据，通过状态转移方程和测量方程进行状态的预测和更新，以获得对系统状态的优化估计。

本文以电力系统的惯量估计为研究对象，基于计及频率响应时空因果相关的电力系统惯量的状态空间模型，引入KF，通过输入相关节点的频率观测值，可以对新能源出力不确定性下的系统惯量进行实时精确估计。图2 是KF 的控制框图，反映了电力系统惯量从状态估计到状态更新的控制流程。图中：ct|t、ct-1|t-1分别为状态矢量矩阵χ在t时刻、t-1时刻估计值的协方差；ωt为t时刻系统噪声；ct|t-1为状态矢量矩阵χ在t-1 时刻预测值的协方差；R为测量噪声协方差矩阵；γt为t时刻观测转换矩阵。

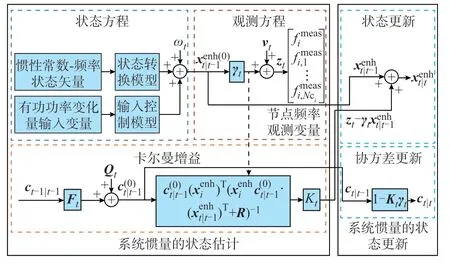
图2 KF 控制框图Fig.2 Control block diagram of KF

图2 中，KF 具体由系统惯量的状态估计和系统惯量的状态更新两部分构成。其中，系统惯量估计模块由上一时刻惯量的估计量xenht|t-1和包括风、光和传统电源有功功率在内的t时刻外部输入量uenht，通过状态估计矩阵Ft，给出初始状态估计值xenh(0)t|t-1；在此基础上，引入电力系统节点频率观测量zt。通过联立状态方程和观测方程，得到系统惯量估计值，为惯量的状态更新提供初始值。在上述工作的同时，状态估计协方差被同时估计，用于衡量每一步状态估计的不确定性，并基于此计算卡尔曼增益。

在系统惯量的状态更新模块中，惯量估计初始值xenh(0)t|t-1及其协方差初始值c(0)t|t-1将被同步更新，针对数据前馈驱动与电力系统频率测量驱动两种方式下惯量估计值的差异，系统惯量估计结果的更新通过卡尔曼增益来判断二者的可靠性，从而决定优化后的状态估计值更倾向于预测模型还是观测模型；协方差估计模块则进一步根据卡尔曼增益系数和观测矩阵对协方差进行更新，从而为下一步状态估计提供更可靠的决策支撑。

4.2 节点频率时空相关的滤波-平滑两阶段惯量估计模型

本文在KF 的基础上，引入非线性电力系统状态估计经常使用的UKF。基于此，引入可以充分利用节点间频率时空相关结果的FLS，从而提高系统惯量估计的准确性和稳定性，并通过降低测量噪声和系统动态的影响，提供更接近于实际状态的系统惯量估计结果。

4.2.1 基于UKF 的惯量初始估计

1）无迹变换

UKF 采用无迹变换（unscented transformation，UT）的确定性采样技术，选择惯性常数-频率状态变量均值附近的一组最小样本点χ矩阵，通过非线性函数传播最小样本点，从而形成新的均值和协方差估计［32］。具体步骤如下。

本文针对改进的惯性常数Henh对应的协方差1、频率的改进状态矢量fenh对应的协方差矩阵1，构建了χ矩阵，通过近似Henh、fenh的均值和协方差来表征非线性状态的不确定性。具体公式如下：

2）预测阶段

（1）将生成的χ矩阵通过状态转移函数ξ（·）进行传播，以在状态变量时序前向滚动中得到预测的惯性常数、频率的χ矩阵：

式中：状态转移函数ξ（·）由式（6）和式（12）的状态方程构成；ut-1为t-1 时刻的输入矢量。

（2）通过传播的χ矩阵计算预测的改进惯性常数状态均值H、改进频率状态均值ft和对应的协方差矩阵c1、c-1。具体计算公式如下：

式中：Qt-1为过程噪声的协方差矩阵，表示系统建模的不确定性；分别为预测的状态变量H、f的χ矩阵的第i+1 列；Wm，i为节点i的χ矩阵的一阶权重；Wc，i为节点i的χ矩阵的二阶权重。

上述方程中的权重计算如下：

式中：Wm，0为节点i的χ矩阵的初始一阶权重；Wc，0为节点i的χ矩阵的初始二阶权重；β为无迹变换参数，可以据应用场景选择。对于频率状态矢量，n=Nci+1；对于惯性常数状态变量，n=1。

3）更新阶段

（1）利用χ矩阵的惯性常数-频率状态的状态均值，计算观测矢量的预测值。

式中：M（·）为观测函数；为χ矩 阵 的 惯 性 常 数状态均值；为χ矩阵的频率状态矢量均值；为节点i的χ矩阵的观测矢量；为χ矩阵的观测矢量的经验平均值。

（2）计算状态矢量和频率观测矢量之间的互协方差、观测矢量的协方差。

式中：c-1为观测矢量χ矩阵的协方差矩阵；c-1为观测矢量-状态矢量χ矩阵的交互协方差矩阵；Rt为观测噪声的协方差矩阵。

（3）根据t时刻处的观测值集合zt，通过计算UKF 增益Kt，得到状态矢量的估计值。

4.2.2 基于FLS 的惯量平滑估计

根据4.2.1 节可知，UKF 更新方程实现了系统惯性常数-频率状态的初始估计，这意味着在t+1 时刻时，可以得到基于所有过去观测和当前观测值zt下的惯性常数-频率状态的估计值。由于相邻节点之间的频率响应存在时空上的因果相关性，换言之，对于系统内任一节点的惯量估计，其因果相关节点在超前时刻的频率值和其自身当前时刻下的频率值具有同样的价值。因此，本文将UKF 与使用超前信息的反向滤波器组合，可以充分利用节点之间频率响应的时空因果关系，使得系统惯量的估计状态更接近于实际状态，从而有效降低系统惯量估计的误差。根据UKF 的系统惯性常数-频率状态初始估计值，得到基于FLS 的平滑估计步骤如下［33］。

对 于 时 刻t，UKF 提 供 了 初 始 估 计 值以及协方差矩阵c。因此，从开始，基于FLS 的递推方程，利用超前时刻下节点频率的观测值，通过时序的反向递推，获取系统惯性常数-频率状态的平滑估计值。

滤波-平滑两阶段惯量估计可以在完成电力系统惯量初始估计的基础上，对惯量估计结果进行修正。由于本文算法引入了具有因果相关节点的频率观测信息，这些观测信息的增加势必会带来噪声，故平滑算法可以有效去除惯量估计结果的噪声，提升惯量估计结果的收敛性，从而使得电力系统惯量的求解收敛到可行解。

4.3 误差分析与模型评价

4.3.1 误差指标

目前，惯量估计误差没有固定的评价标准，本文基于电力系统节点频率以及节点有功功率的测量值，采用式（6）对系统节点的惯性常数进行逆运算，得出电力系统惯量的理论值，从而计算惯性常数理论值与估计值之间的平均绝对误差。具体如下：

式 中：H、H分 别 为 电 力 系 统 节 点j在t时 刻 下 的惯性常数理论值、估计值；分 别 为 节 点j在t时刻的实际频率一阶导数、有功功率变化实际值；T为惯量估计周期；εj为节点j的惯性估计误差。

结合式（2），计算系统t时刻惯性常数估计值H、理 论 值H，并 在 此 基 础 上 引 入 系 统 惯 量 估计误差εsys，用于衡量整个电力系统在周期T内的惯量估计误差。

4.3.2 对照模型

1）扩展卡尔曼滤波估计方法

Bucy、Sunahara 等人提出并研究了扩展卡尔曼滤波（extended kalman filter，EKF），并将KF 算法进一步应用到非线性领域。EKF 的优势在于其状态转移模型和观测模型可以是可微的非线性函数，是电力系统惯性常数-频率状态估计的传统算法。具体理论模型推导详见文献［34］。

2）粒子滤波估计方法

粒子滤波（particle filters，PF）是一种用于非线性系统的滤波算法，其核心思想是通过一组粒子来估计随机过程的后验分布，并利用加权粒子来更新预测。PF 的优势在于其可以从所需分布中生成样本，而不需要对状态空间模型或状态分布提前做出假设，是电力系统状态估计的常用算法之一。具体的理论模型推导详见文献［35］。

3）基于惯性中心频率的估计方法

基于惯性中心频率的惯量估计是一种用于电力系统整体惯量估计的传统方法，利用惯性中心节点的频率测量信息，通过惯性常数-频率状态的摆动方程构建系统惯量的状态方程，进而利用UKF 和FLS的组合算法对系统惯量进行估计。其中，系统惯量中心频率的计算公式为：

式中：fCOI为系统的惯性中心频率，由系统内所有同步机转速按其转动惯性常数加权求和得到；fG，m为同 步 机 转 速；HG，m、SG，m分 别 为 同 步 机 转 动 惯 性 常数、额定容量；M 为同步发电节点构成的集合；m为同步发电节点。

基于此，定义系统的惯性中心频率和系统惯性常数Hsys为状态变量，即xenh=［Hsys，fCOI］，定义所有联络线有功功率变化量ΔPℓ，i组成输入变量，即uenh=[ΔP]ℓ，i，ℓ ∈Li，构造基于惯性中心频率的状态方程如下：

按照本文第4 章的建模步骤，建立基于惯性中心频率的系统惯量估计模型。

4）本文方法与对照组比较分析

根据上述传统状态估计算法，本文共设置了4 组对照模型，用于验证分析本文所提算法的有效性，所提算法与对照组模型的对比分析如表1 所示。本文设置的对照组按照控制单一变量的基本原则来设定，打“√”表示该模型利用了这种算法。表中：对比模型1 和对比模型5 用于验证Granger 时空因果相关性检验，对比模型2 用于验证FLS 算法在系统惯性常数-频率状态估计中的有效性，对比模型3 和对比模型4 则用于验证UKF 算法的优势和适应性。

表1 本文所提算法与对照组模型对比Table 1 Comparison of proposed algorithm and control group model

5 算例分析

5.1 模型介绍与仿真验证

本文在IEEE 39 标准电网拓扑结构的基础上，增加多组由下垂控制的风力发电机组，模拟风电场并网所提供的惯量。此外，增加通过虚拟惯量控制的光伏发电机组，模拟光伏电站并网所提供的惯量，如图3 所示。

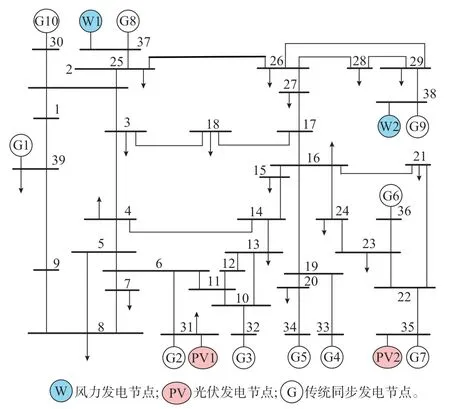
图3 改进的IEEE 39 节点系统Fig.3 Improved IEEE 39-bus system

该系统总共包括10 个发电节点、39 条母线。本文利用三相并联负载模型来对节点负荷和主网负荷进行等值。假设仿真数据足够接近真实情况，在仿真的0～30 s 内通过实际风速和辐照度分别设置风电和光伏的出力数值，从而生成高占比新能源电力系统运行的数据样本。

本文电力系统惯量估计过程中的数据来源于PMU 测量数据，数据使用可分为离线计算和在线监测两种方式。其中，离线计算用于分析系统内务节点频率间的时空因果相关性，通过PMU 测量并上传数据至云平台上，以临近待估时刻的时间段作为分析周期，计算务节点的时空因果相关性矩阵；在线监测用于系统惯量实时估计，基于频率-惯量的状态空间模型对系统内务个节点的频率进行实时估计。案例分析包括发电节点的惯性常数估计和系统惯量估计，对于单一发电节点的惯量估计，计算方式为分散式计算；对于电力系统的惯量估计，计算方式为集中式计算。系统内务发电节点装机容量如附录B 表B1 所示，其中，节点31、35、37、38 含新能源场站并网，当风电/光伏在上述节点渗透率为100%时，整个系统的新能源装机占比可达66.7%。风电场站的控制方式为下垂控制；光伏场站的控制方式为虚拟惯量控制；风电场站W1、风电场站W2 的虚拟惯量常数分别设置为4.75、3.52 s；光伏场站PV1、光伏场站PV2 的虚拟惯量常数分别设置为4.89、3.64 s。

5.2 有效性验证

5.2.1 节点频率时空相关量化的有效性验证

本文选取了某一时段内电力系统拓扑节点间的频率因果关系分析结果，如图4 所示。图中：C（i，j）指节点i和节点j的频率具有因果关联关系。

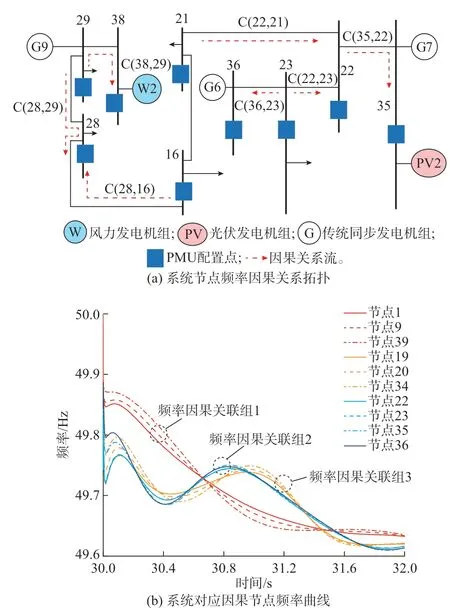
图4 系统各节点频率响应因果相关性示意图Fig.4 Schematic diagram of causal correlation of frequency response of each node in system

图4（b）展示了图4（a）中9 个节点的频率测量曲线。从图中可以看出，在同一时刻下，不同节点的频率测量值之间呈现明显的时空因果相关特性，对于任意一个节点，可以有临近的多个节点与其频率呈现因果关系。此外，图4（b）展示了系统频率在时序上超前-滞后的特性与因果相关性之间的关系，不同频率因果相关组之间的频率曲线幅值差距较大。其中，节点1 和节点36 的频率最低点的差值超过0.2 Hz，处于同一频率因果相关组的频率曲线幅值差异小，仅存在些许的横向误差。因此，同一频率因果相关组对应的节点集合，其测量数据可以互补利用，减少由于单一节点频率测量误差所带来的惯量估计误差。从仿真层面上解释了因果分析对于节点频率估计模型输入筛选的现实意义。

基于此，本文基于Granger 因果检验算法，统计分析了某一时刻下用于估计节点惯性常数的时空因果相关节点集合，如附录B 表B2 所示。对于不同节点而言，用于惯量估计的频率因果相关集合不同，尤其是面向新能源并网的节点，其频率因果相关集合元素相较于常规电源节点少，频率响应相对独立，这也体现了分类估计常规场站和新能源场站惯量的必要性。另外，针对系统内的任一节点，其他节点的频率既有可能是其原因节点，也有可能是其结果节点。因此，其他节点超前或滞后于该时刻的频率信息，对当前时刻下这一节点的频率惯量估计具有同等的价值。这一结论也体现了引入FLS，并充分利用其他节点在超前时刻下的频率观测值对节点的惯性常数估计具有重要意义。

为进一步验证滤波-平滑两阶段惯量评估方法对系统运行状态的适应性，本节在改进的IEEE 39节点系统中设置多个位置持续扰动以模拟实际电网频率波动场景，在t为0～15 s 和t为15～30 s 时，负荷扰动位置分别位于节点21、22、23、24 和节点10、11、12、13。负荷扰动节点的位置如附录B 图B1所示。

除了模拟负荷扰动工况之外，本文分别增加了常规场站、风电场以及光伏电站切出的场景，用于对比分析不同频率测量输入方式下系统惯量估计的效果，如表2 所示。

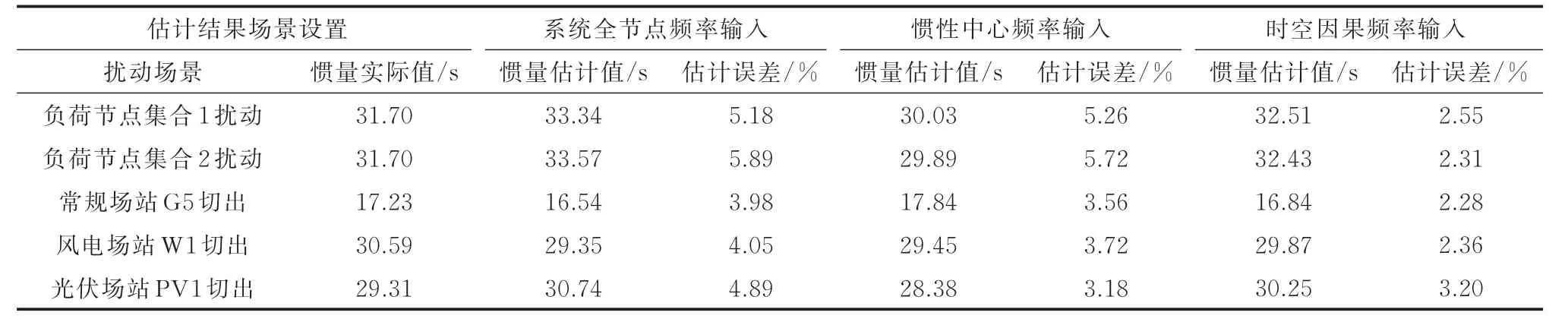
表2 不同频率测量输入方式下系统惯量估计效果的对比Table 2 Comparison of system inertia estimation effect with different frequency measurement input methods

从表2 中可以看出，在大部分场景下，时空因果频率输入下的系统惯量估计精度高且泛化能力较强。由于惯性中心频率仅仅是对务节点频率观测信息的平均，在这一过程中，可以将频率测量误差进行分摊，但是无法准确校正每个节点的频率测量误差。而时空因果频率的输入不仅可以对系统惯量进行估计，也可以对务节点的惯量进行估计，并利用务节点之间的时空因果相关性对某一节点的惯量估计结果进行校正。因此，泛化能力较强且在部分节点频率测量信息缺失的前提下，能够保证系统惯量的估计精度。

5.2.2 UKF 有效性验证

基于4.3.2 节中所设置的对照组，本文引入EKF 和PF 两种系统惯量传统估计算法，验证UKF对系统惯量进行状态估计的有效性。本文选取某一估计周期（0～6 s）内，基于3 种方法对电力系统发电节点的惯量估计结果进行对比分析，对比曲线如图5 所示。图中：εPF、εUKF、εEKF分别为PF、UKF、EKF算法的误差，括号内的数据表示对应算法的收敛时间。

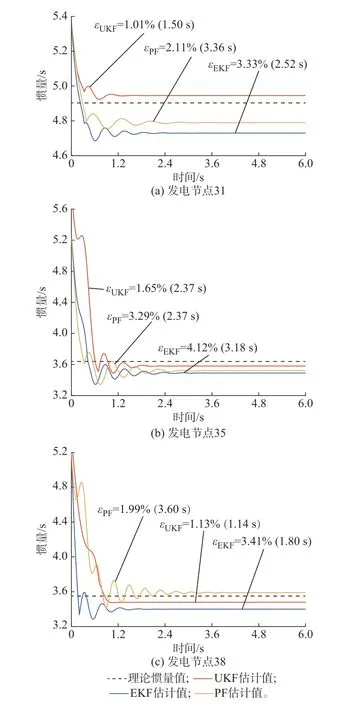
图5 不同滤波算法下的电力系统惯量估计结果Fig.5 Power system inertia estimation results with different filtering algorithms

本文选取发电节点31、35、38 作为分析对象。从图5（a）、（b）、（c）中可以看出，3 种算法收敛至稳定的估计结果需要一定的时间，收敛时间均在3.7 s以内。当节点惯性常数的估计值达到收敛之后，其与理论惯量之间的误差大部分维持在2%以内。

从图5 中UKF、EKF 和PF3 种状态估计算法的结果可以看出，与PF 算法相比，EKF 算法的收敛速度较快，而估计精度较低。这是由于EKF 算法对于状态空间的线性化要求比较严格，本文针对的是系统惯量非线性估计，且考虑其他相关节点的频率响应，估计结果维度高。因此，EKF 算法的估计效果不佳。而PF 算法的计算复杂度将会随着粒子数目的增加而增加，对于高维状态空间，粒子数目大幅度增加，从而导致计算量增大，且收敛速度变慢。相比之下，本文所提的UKF 算法具有较高的估计精度和较快的收敛速度。

5.2.3 FLS 有效性验证

根据4.3.2 节中所设置的对照组，利用对比模型2，即将本文所提模型移除FLS 后，与本文算法进行对比，用于验证引入FLS 的必要性。绘制有无FLS模型下的节点惯性常数估计结果曲线如图6 所示。

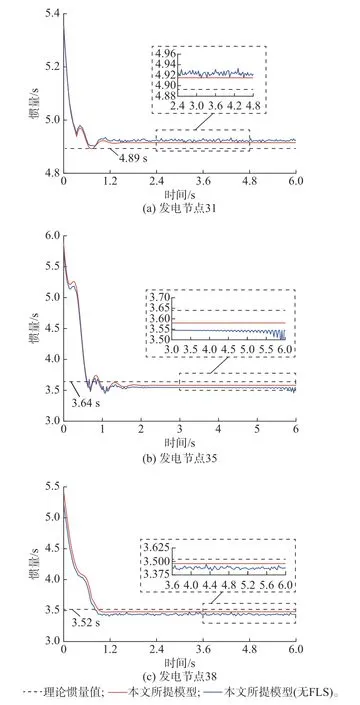
图6 有无FLS 的惯量估计结果对比Fig.6 Comparison of inertia estimation results with and without FLS

可以看出，FLS 可以对节点惯性常数估计的时序过程进行平滑，并且收敛之后的惯量估计值更接近于理论惯量值。一方面，这是由于FLS 的引入充分考虑了其他节点频率的未来观测值，从而为节点惯性常数的估计提供了更多、更有效的数据基础；另一方面，由于FLS 可以平抑惯量时序的波动幅度，从而可以在同一判敛准则下，使得结果收敛更快。因此，FLS 的引入有助于提升惯量估计的准确性和收敛速度。

5.3 算法适用性分析

5.3.1 不同新能源渗透率下的算法适用性

基于5.1 节，本文通过增加节点31、35、37 和38的风电/光伏装机容量，提升改进IEEE 39 节点系统的新能源渗透率。选取当风电/光伏新能源渗透率达到25%、50%、62.5% 和66.67% 下的发电节点31、35、38 的频率曲线作为分析对象，如图7 所示。

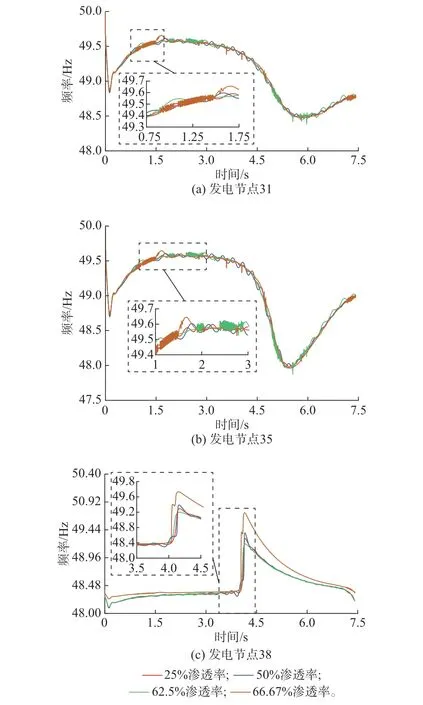
图7 不同新能源渗透率下系统节点频率变化曲线Fig.7 Frequency variation curves of system buses with different renewable energy penetration rates

从图7 中可以看出，随着风电/光伏新能源装机容量的增加，节点频率的波动程度也随之增大。这是由于风电/光伏的不确定性导致了节点频率在时序上的波动。当新能源渗透率为25～50%时，系统节点的频率变化呈现缓慢波动的趋势；当新能源渗透率在60%以上时，系统节点频率呈现大幅度、聚集性剧烈波动。随着新能源渗透率的增加，节点38的频率出现陡增，在这一情形下更需要对新能源电力系统惯量和频率进行提前估计。同时，验证了高比例新能源电力系统频率的时序特性，体现出了新能源电力系统惯量估计的必要性。根据4.3.1 节提出的新能源电力系统惯量评价指标，计算并统计发电节点的惯量估计结果如附录C 表C1 所示。

5.3.2 不同频率扰动场景下的算法适用性在新能源渗透率为66.7%的基础上，当t=5 s时，分别在发电节点34、37 和31 退出装机为50 MW的常规场站（G5）、120 MW 的风电场站（W1）和100 MW 的光伏发电场站（PV1）。设定一次调频死区为0.033 Hz，其中，时间窗1 为一次调频响应之前，时间窗2 为一次调频响应之后，上述3 种场景下电力系统的频率响应曲线如图8 所示。

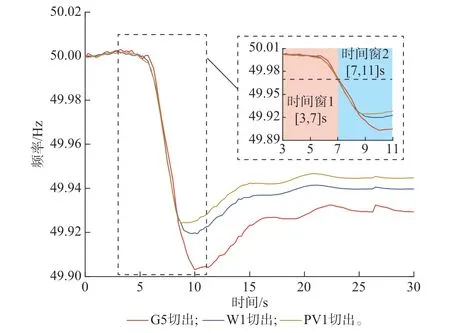
图8 不同扰动场景下的系统频率响应曲线Fig.8 Frequency response curves of system in different disturbance scenarios

从图8 中可以看出，本文选取了3～11 s 内不同场景下系统频率扰动的情景作为惯量估计的分析对象，t=5 s 时为扰动发生时刻，其中，时间窗1 描绘了电力系统频率在扰动前（发电机一次调频死区内）的变化情况；时间窗2 描绘了电力系统在一次调频死区之外（恢复时间段内）的变化情况。目的是分析不同类型电源节点的扰动对电力系统频率的影响，进而分析对电力系统惯量估计效果的影响。附录C 表C2 给出了不同频率扰动场景下的电力系统惯量估计结果。其中，时间窗1（t为3～7 s）描绘了电力系统频率在扰动前（发电机一次调频死区内）的变化情况；时间窗2（t为7～11 s）描绘了电力系统在一次调频死区之外（恢复时间段内）的变化情况。

6 结语

本文分析了新能源电力系统惯量的主要来源并给出了计算方案，提出了基于Granger 因果检验算法的频率响应时空相关性量化方法，建立了考虑节点时空相关性的系统惯性常数-频率状态空间模型。此外，提出了基于UKF 和FLS 的系统惯量两阶段估计方法，并给出了系统惯量估计误差的评价指标，基于改进的IEEE 39 节点系统验证了所提方法的有效性。主要结论如下：

1）电力系统内务个节点的频率具有超前-滞后的时空因果相关特性，将具有时空因果相关性的节点的频率测量信息纳入惯量估计的观测量中，可以提升系统惯量估计的准确性。

2）利用UKF 和FLS 的电力系统惯量两阶段状态估计方案，通过分布式与集中式相结合的计算方式，可以保证从单一发电节点到全系统惯量估计的准确性与收敛速度。

3）随着新能源渗透率的提升，系统频率波动性增大、系统惯量估计难度增加，所提方法可以适应不同新能源渗透率下的系统惯量估计。同时，在频率扰动场景下仍然可以保持较高的惯量估计精度，所提方法具有泛化能力和鲁棒性。

本文所提的惯量估计方法的有效性可以在新能源电力外送、跨区直流输电等实际工程中得到进一步应用和验证。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。