能量视角下的电力系统惯量

丁 磊，郭一忱，鲍威宇，张陈辉，王志浩，宋国兵

（1.山东大学电气工程学院，山东省济南市 250061；2.西安交通大学电气工程学院，陕西省西安市 710049）

0 引言

物理上，惯性被定义为一个物体阻碍其状态变化的能力［1］，这种惯性的度量被称为惯量，与物体的运动形式相对应。对于最常见的平移运动，物体的质量被看作是其惯性的度量。旋转运动是另一种常见的运动形式，其惯性的度量是机械旋转惯量。

同步机（本文以燃煤发电机组为例）主导的电力系统的能量供应链包括电气网络、发电机、汽轮机、锅炉、燃料供应系统等［2］。由于同步机在电磁尺度上表现为电压源，并有大量的蓄热和稳定的燃料供应，电气网络和锅炉的动态一般被忽略［3］。发电机和汽轮机的旋转质块动态成为能量供应链动态的核心矛盾［4］。作为影响旋转质块动态的主导因素，机械旋转惯量被代指为系统惯量，在阻碍旋转转速及频率的变化上起到非常重要的作用［5］。

大规模新能源的接入替代了同步机，导致机械旋转惯量的大幅下降［6-7］，形成了所谓低惯量系统。惯量降低造成频率变化和偏移更大，影响设备效率和性能，威胁系统安全和完整性［8］。

为了应对惯量下降，提出了许多控制方法，使得新能源可以模拟同步机的惯量响应［9-10］。但低惯量电力系统面临的挑战不仅仅是旋转惯量的减少和补偿问题［11］，新能源通过控制和物理连接与同步机耦合［12］，使得整个电力系统的能量供应链的形式和参数都发生了根本性的变化。频率和旋转转速的动态更加复杂，机械旋转惯量的主导作用被削弱［13］，不能再被代指为系统惯量。

在这种情况下，什么是电力系统惯量？惯量在电力系统动态中起什么作用？电力系统安全运行对惯量的要求是什么？这些科学问题需要被重新回答，并涵盖同步机主导、新能源主导以及同步机与新能源混合系统，以指导对未来电力系统的认知、分析与设计。

本文首先回归到惯量是阻碍物体状态变化能力的度量的本质定义，将惯量形式从机械旋转惯量扩展到热惯量、电惯量和流体惯量，以涵盖电力系统中的机械旋转运动、电子运动和分子运动。将电力系统建模成一个流过能量流的多尺度能量供应链，并识别出能量存储单元和能量传输通道。同一尺度上存储惯量和通道惯量组成的“惯量对”决定了该尺度的动态，存储惯量需求背后的根源是能量需求，即存储单元需要有足够的瞬时可释放能量来应对传输通道因采用自身物理结构或反馈控制而存在的能量补充滞后；总的尺度上，不同尺度的多个“惯量对”决定了时域上的序贯动态和频域的级联滤波特性，整个能量供应链需要存储足够的本地能量支撑分散控制，直到通过集中控制改变能量供应链的输入，实现能量流再平衡。

能量视角下的电力系统惯量认知，有助于评估未来新型电力系统的惯量需求，对新能源参与有功控制的方法设计提供理论指导。

1 广义惯量

在物理上，惯性被定义为一个物体阻碍其状态变化的能力，其大小用惯量度量［14］。对一个质量为m、以恒定速度做直线运动或静止的质块，速度v是其状态变量，施加外力F后速度不能突变，以F=mdv/dt的方式变化；质量m被看作是该质块惯性的度量，其大小反映了外力作用下质块抵御自身速度变化的能力［15］。

类似地，对于一个绕轴转动的刚体而言，转速ω是其状态变量，施加转矩T后转速不能突变，以T=Mdω/dt方式变化；机械旋转惯量M被看作旋转刚体惯性的度量，其大小反映了在外力作用下刚体抵御自身转速变化的能力。

显然，物体惯量与物体状态量是一一对应的，惯量和状态量总是成对出现，例如，m和v、M和ω。具有惯量的物体的一个关键性质是可以存储能量或物质，其状态不能发生突变，这类物体也称惯性元件。

在电力系统中，惯量往往都是指发电机和汽轮机的旋转质块所对应的机械旋转惯量［16-17］，对应的状态量为转子转速以及转子转速所决定的电气频率，所以惯量和状态量为M和ω［18］。但实际上，电力系统中，不仅仅包括与旋转质块的旋转运动相关的转速（频率）动态［19］，还包括与其他运动形式相关的动态。例如，电压、电流的变化与电子运动相关，蒸汽流动和锅炉压力变化与分子运动相关。为了描述与电子和分子运动相关的动态，惯量的定义要被进一步扩展［20］。

以燃煤发电机组主导的电力系统为例，本文定义了电容、电感、锅炉、蒸汽通道、燃料供应系统的惯量，如表1 所示。表中：D′为蒸汽通道的蒸汽速率；H为蒸汽的焓；d为蒸汽通道输入端能量注入的速率；Qw为锅炉输入端能量注入的速率；r为燃料供应通道输入端能量注入的速率；K1为燃料的能量密度；rb为煤粉进入锅炉的速率。对电容和电感定义的电惯量表示阻碍电压和电流变化的能力；对锅炉定义的热惯量表示阻碍压力变化的能力；对蒸汽通道和燃料供应系统定义的流体惯量表示阻碍能量流速变化的能力。

表1 惯量的定义Table 1 Definition of inertia

惯性元件都具备能量存储能力，根据其在能量流动态过程中起到的作用不同，上述惯性元件可进一步分为能量存储单元和能量传输通道。能量流动态过程中，存储单元的状态量表征剩余存储能量的大小；传输通道的状态量表征能量流速的变化。电容、旋转质块和锅炉可以看作存储单元；而电感、蒸汽通道和燃料供应系统可以看作传输通道。

2 多尺度统一模型与惯量对

将上述元件组合连接，可以得到3 个子系统：电气网络子系统、转子汽机子系统和锅炉燃料子系统，如图1 所示。

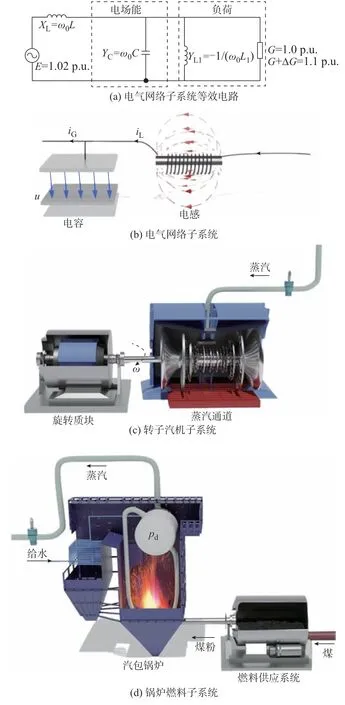
图1 子系统示意图Fig.1 Schematic diagram of subsystems

2.1 多尺度统一模型与惯量对

图1（a）为描述电气网络子系统动态的等值模型。图中：ω0为工频角速度；有功负荷由并联电导G表示；无功负荷由并联电抗L1表示，其导纳为YL1；ΔG为并联电导的增量；并联电容C表示对地电容和本地无功补偿的综合作用，其导纳为YC；串联电感L表示理想无损线路和同步机等效的等效电感，其等效阻抗为XL。在模型中，将同步机表示为一个内电势为E的理想电压源串联等效内阻抗，这在能量流变化的非常短的初始时间内（指电磁尺度）是有效的。

忽略与并联电抗L1相关的动态，电气网络子系统的动态可以表示为：

式中：De为电气网络阻尼系数；ΔU→C为并联电容电压的变化值；U→C0为并联电容电压初始值；ΔI→L为串联电感电流的变化值；“→”表示电气量的矢量形式。电气网络子系统可以看作两个惯性元件的串联，即一个存储单元（电容）和一个传输通道（电感），如图1（b）所示。图中：iG为电容C输出电流的瞬时值；iL为电感L的电流瞬时值。

2.2 转子汽机子系统模型

转子汽机子系统的动态可以表示为［2］：

式中：KL为系统负荷频率阻尼系数；Δω为转子转速的变化量；ΔPm为机械功率的变化量；ΔPe为电磁功率的变化量；Tv为同步机一次调频响应时间常数；KG为同步机一次调频的下垂系数。转子汽机子系统可以看作两个惯性元件的串联，即一个存储单元（旋转质块）和一个传输通道（蒸汽通道），如图1（c）所示。

2.3 锅炉燃料子系统模型

以汽包燃煤锅炉为例，锅炉燃料子系统的动态可以表示为［21］：

式中：Cb为锅炉的蓄热系数；K3为汽轮机调门增益；ut0为汽轮机调门开度初值；Δpd为锅炉汽包压力的变化量；Δrb为煤粉进入锅炉速率的变化量；ΔPr为锅炉释放的蒸汽变化量；Tf为一次燃料的响应时间常数；Kr为锅炉一次燃料的控制增益。锅炉燃料子系统可以看作两个惯性元件的串联，即一个存储单元（汽包锅炉）和一个传输通道（燃料供应系统），如图1（d）所示。

2.4 多尺度统一模型

3 个子系统都可以建模成图2（a）所示的统一模型，能量存储单元表示为蓄水池，能量传输通道表示为水管。

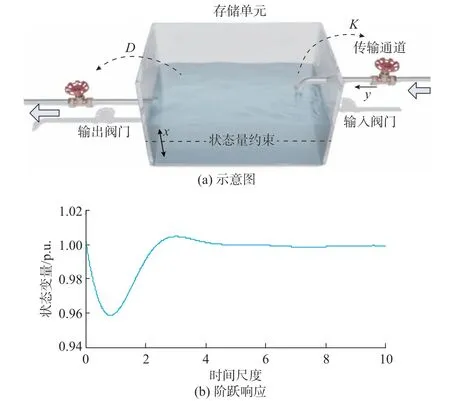
图2 多尺度统一模型Fig.2 Unified model for multiple scales

其动态表示如下：

式中：J为统一模型的存储惯量；T为通道时间常数；Δx为存储惯量状态x的变化量；Δy为通道惯量状态y的 变 化 量；ux为 统 一 模 型 的 有 功 扰 动；D和A分 别为存储单元和传输通道的阻尼系数；B、K为统一模型的控制系数。务尺度子系统与统一模型参数的对应关系见附录A 表A1。

式（4）的第1 个方程描述了给定扰动下存储单元的动态，第2 个方程描述了传输通道的动态。一旦在左侧输出阀门增加需求ux，将造成能量存储单元的状态量变化Δx，存储惯量J将阻止这一变化。随着Δx的变化，一方面，在阻尼系数D的作用下，左侧输出阀门的流量会略微变小；另一方面，通过控制或物理连接右侧输入阀门会调大KΔx，增加通道流量Δy，但通道流量的增加受通道时间常数T影响而不能瞬时到位。

在这个过程中，存储单元在tn时刻达到状态量的最低点，ts时刻达到准稳态，其偏差Δx∞=ux/(D+KB/A)。还有一种特殊情况，即K=0 或T=∞的情况，意味着通道流量不随存储水平变化，存储单元状态量将最终达到准稳态，其偏差Δx∞=ux/D。

对一个已知扰动ux，给定了阻尼和控制系数{D，A，B，K}后，统一模型的动态主要由[J，T]，即惯量对所决定。J和T都可以看作惯量，前者是存储惯量，后者是通道惯量。要想得到期望的动态响应，惯量对必须合理匹配。对相同的存储元件状态偏移，大的T需要配合大的J，小的T允许J小一些。

实际上，统一模型是一个近似的等价模型；3 个子系统之间有微小的差别，主要体现在右侧输入阀门的位置及其控制上。电气网络子系统中，物理连接决定了右侧输入阀门在传输通道的左端；而转子汽机子系统和锅炉燃料子系统中，控制逻辑决定了右侧输入阀门在传输通道的右端。另外，电气网络子系统和转子汽机子系统右侧输入阀门的控制均采用有差控制，而锅炉燃料子系统往往采用比例-积分（PI）控制。这些微小差别会在一定程度上影响子系统的动态细节，但仍然可以用统一模型来分析总结动态过程中的一般化规律特征。

值得一提的是，本文仅讨论施加在左侧输出阀门的扰动，即引起能量消耗先发生变化的扰动。左侧可能出现“大幅度”阶跃扰动，并直接抽取存储单元的存储能量，存储单元状态量易出现较大偏差，系统动态过程剧烈。右侧输入阀门施加的扰动，即能量供给发生变化的扰动，其扰动幅度相对较小。此外，右侧阀门扰动首先传入传输通道，再传入存储单元，该过程中传输通道对扰动起到缓冲作用，进一步减小了右侧阀门扰动对存储单元的冲击，存储单元的状态量的变化较为平缓。因此，本文不再讨论右侧阀门扰动下系统的动态过程。此外，本文重点讨论单机等值的能量供应链，未考虑多机的惯量时空分布特性，后续将开展相关研究。

3 多尺度能量供应链及其动态特性

3.1 多尺度能量供应链

上述3 个子系统可以连接起来，形成完整的多尺度能量供应链，如图3 所示。为了将3 个子系统连接在一起，需要考虑子系统之间的关系。转子汽机子系统的能量流输出对应电气网络子系统的能量流输入，即，其中，为同步机内电势的空间矢量，Δ为并联电感电流空间矢量的共轭；锅炉燃料子系统的能量流输出对应转子汽机子系统的能量流输入，即ΔPr=-KGΔω；锅炉燃料子系统的能量流输入 ΔPc来源于一次燃料，即ΔPc=-KrΔpd。整个系统的动态可表示为：

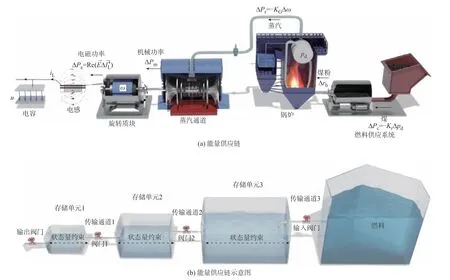
图3 多尺度能量供应链与能量流Fig.3 Multi-scale energy supply chain and energy flow

这是一个单输入、单输出的串联系统，其输入是一次能源或燃料，输出是有功需求和损耗之和。燃煤发电机组主导的系统包含电气网络子系统、转子汽机子系统和锅炉燃料子系统，其包含了3 个存储单元和3 个传输通道。因此，在阻尼和控制系数都确定的情况下，整个系统动态由6 个惯量，也就是3个“惯量对”所决定。

存储惯量和通道惯量可以以系统流过的额定能量流速为基准，标幺化成时间常数，即惯量常数。存储惯量常数表示以额定能量流速释放存储能量需要的时间，而通道惯量常数表示在外加额定压力下能量流速从零到额定值所需要的时间。惯量常数的典型值如附录A 表A2 所示。

可以注意到，系统中有3 个尺度：惯量对［J1*，T1*］所决定的毫秒级的电磁尺度；惯量对［J2*，T2*］所决定的秒级的机电尺度；惯量对［J3*，T3*］所决定的分钟级的机炉尺度。这3 个尺度相差10 倍以上，它们的动态彼此之间可以被认为是解耦的。3 个惯量对构成了系统的多尺度惯量体系，决定了整个系统的动态。

3.2 事件扰动下能量供应链时域序贯动态特性

在有功事件扰动（如发电机跳闸或负荷突增等）下，能量供应链的输出端会出现显著的能量流净增加［22］，多尺度能量供应链会经历从小尺度到大尺度传递的时域序贯动态，如图4 所示。

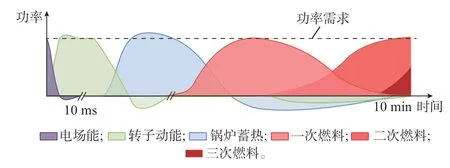
图4 能量流不平衡作用下的能量供应链时域序贯动态Fig.4 Time-domain sequential dynamic of energy supply chain under energy flow imbalance

以初始扰动ΔPD为例，相当于增加一个并联电导ΔG在负荷节点上，电流流过并联电导，抽取电场能使得节点电压下降。这使得发电机和负荷之间的电压差增加，输电线路的电流增加，从而抽取旋转动能来补充减少的电场能。这一动态在几个毫秒内达到一个新的平衡，电压、电流达到准稳态值。

在准稳态电流Δid∞下，施加在旋转质块上的不平 衡 功 率ΔPe=EΔid∞=ΔPD-ΔPd(Δu∞，0)，其中，扰动功率在准稳态电压Δu∞和阻尼作用下变化量为ΔPd，故ΔPe略小于ΔPD。抽取旋转动能会引起转速的下降，如果转速变化足够大，调速器动作打开蒸汽轮机的阀门，从锅炉中抽取热能来补充减少的旋转动能。这一动态过程在几秒内将达到一个新的平衡，转子转速和蒸汽流量达到准稳态。

准稳态蒸汽流量下，施加在锅炉上的不平衡量ΔPr=-KGΔω∞=ΔPe-ΔPd(Δu∞，Δω∞)，其中，扰动功率在准稳态电压Δu∞、准稳态频率偏差Δω∞和其对应的阻尼作用下变化量为ΔPd，故ΔPr略小于ΔPe。如果没有锅炉汽机协调控制系统（CCS），汽包压力会持续下降。在CCS 作用下，燃料会增加以补充减少的热能［23］。

由于整个过程中3 个时间尺度可以很好地解耦，在研究某个时间尺度的动态时，可以假定前一个时间尺度已经达到准稳态，而后一个时间尺度的状态还没有变化。

本文只讨论施加在最左侧输出阀门上的扰动引起的动态，即引起能量消耗先发生变化的扰动，在这种情况下系统动态较为剧烈，惯量起显著作用；而不讨论最右侧输入阀门施加扰动对应的动态，即引起能量供给先发生变化的扰动，这种情况下的系统动态往往平缓得多。

3.3 负荷波动下能量供应链频域级联滤波特性

负荷波动可以看作多个频率、不同幅值的正弦分量叠加，假设其中一个正弦分量的频率为f。本文提出的多尺度“惯量对”统一模型可以表示为图5 所示的闭环传递函数。

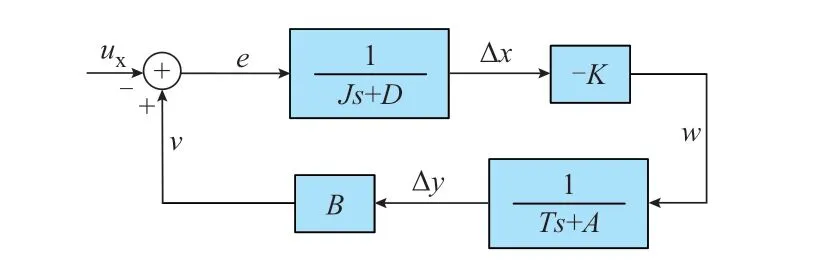
图5 能量供应链多尺度统一模型传递函数框图Fig.5 Block diagram of transfer function of multi-scale unified model with energy supply chain

图5 中，施加在左侧输入阀门上的能量流波动为ux=sin(2πft)，e为存储单元承担的波动分量。在控制作用下，传输通道根据Δx改变输入的能量流w，经传输通道后输出v。v与e共同应对能量流波动ux，即

e、w、v可表示为：

其中

基于式（7）可绘制出图6 所示“惯量对”闭环幅相特性。可以看出，在频率f1、f2、f3划分的不同频段内，e、w、v的波动特性存在明显差异。

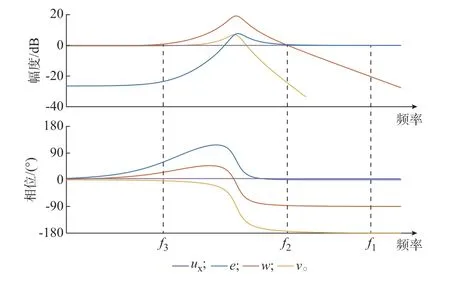
图6 “惯量对”的闭环幅相特性Fig.6 Closed-loop amplitude-phase characteristics of“inertia pairs”

1）f≥f1时：e的幅度近似等于ux，在存储单元的滤波作用下，w、v的幅度小于0.1ux，可近似忽略；波动完全由存储单元承担，不向后一尺度传播。

2）f2＜f＜f1时：存 储 单 元 的 滤 波 效 果 变 弱，w出现明显变化，波动开始向后一尺度传播。但由于传输通道的滤波作用，v的幅度仍然较小，即后一尺度的响应还未到位。

3）f3＜f≤f2时：传输通道的滤波效果变弱，v与e的幅度相近，但由于两者之间存在较大的相位差，存储单元和传输通道间发生振荡，e、v、w的幅度大于ux。

4）f≤f3时：存储单元和传输通道的滤波效果很弱，e近似为0，v与ux的幅度基本相同，波动完全传播至后一尺度。

需要说明的是，对于电气网络子系统来说，w代表电感两端的电势差，不代表能量流。在附录A 表A2 给出的典型参数下，3 个子系统的f1、f2、f3如附录A 表A3 所示。如上文所述，“惯量对”表现出对负荷波动的低通滤波特性，多尺度的“惯量对”串联而成的能量供应链在能量流波动下表现出多尺度频域级联滤波特性，如图7 所示。

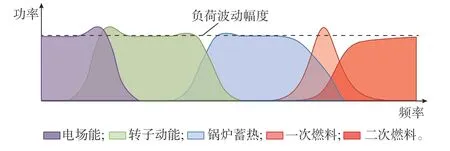
图7 能量流波动作用下的能量供应链频域级联滤波特性Fig.7 Frequency-domain cascading filtering characteristics of energy supply chain under energy flow imbalance

4 能量视角下的惯量需求

电力系统为什么需要惯量？最主要的原因是利用惯量阻碍状态的变化，将状态偏移限制在一定范围内。如果状态与系统变量相关，最大允许状态偏移量由系统安全约束或供电质量决定，如电压或频率；否则只是单个设备的状态，最大允许状态偏移量由该设备安全约束决定，如锅炉压力。一般来讲，单个设备状态允许的偏移要远大于系统变量允许的偏移。

值得一提的是，虽然惯量在限制状态偏移的同时降低了状态的变化率，但动态过程对状态变化率一般没有特别要求，除了人为设计的控制，例如，基于频率变化率的防孤岛保护。

由图2 所示多尺度统一模型可知，对于任意一个能量供应链的子系统而言，在发生有功事件扰动后，扰动引起的能量流不平衡首先抽取存储单元的能量，再由传输通道进行补充。在此期间，存储单元的能量存储水平将经历一个动态过程，其状态量先下降后上升，最后达到新的稳态。假设存储单元的状态量在tn时刻下降到最低点xn，而其最大的允许偏移量为xlimit，则需要满足xn＞xlimit这一不等式关系，以确保该尺度的动态安全。由于xn的大小受存储惯量影响，上述不等式关系也可以决定系统动态安全对惯量的需求。

为了计算能量视角下的惯量需求，首先对3 个子系统的动态方程式（1）至式（3）进行积分，得到子系统的能量平衡关系，进一步总结归纳出与多尺度统一模型对应的能量平衡关系，并在此基础上分析存储单元的能量需求和惯量需求。

4.1 电气网络子系统的能量平衡关系

电气网络子系统的能量平衡关系可以表示为：

式中：UC和IL分别为电容电压、电感电流的幅值；下标“d”表示直轴分量；下标“0”表示变量的初值；ΔEout为多抽取的能量；ΔEin为多注入的能量；ΔEChannel，E为 交 流 电 感L中 的 磁 场 能 变 化；ΔEstorage，E为交流电容中电场能的变化；下标“E”表示电气网络子系统中相关变量。

4.2 转子汽机子系统的能量平衡关系

转子汽机子系统的能量平衡关系可以表示为：

即

式中：下标“R”表示转子汽机子系统中相关变量；ΔEChannel，R为 蒸 汽 通 道 中 能 量 的 变 化 量；ΔEstorage，R为转子的动能变化量。

4.3 锅炉燃料子系统的能量平衡关系

锅炉燃料子系统的能量平衡关系可以表示为：

即

式中：下标“B”表示锅炉燃料子系统相关变量；ΔEChannel，B为 燃 料 通 道 中 的 能 量 变 化 量；ΔEstorage，B为锅炉蓄热量的变化量。

4.4 存储单元的能量需求和惯量需求分析

对上述3 个子系统的能量平衡关系进行归纳，可以得到多尺度统一模型在有功扰动后的能量平衡关系，表示为：

由式（15）所表示的能量平衡关系可知，多抽取的能量ΔEout等于多注入的能量ΔEin、存储单元的能量变化量ΔEstorage和传输通道的能量变化量ΔEChannel三者之和。在通道惯量的作用下，传输通道的能量补充具有滞后性。因此，存储单元应当存储一定的能量（称为“瞬时可释放能量”），以便于在传输通道补充到位前，依靠释放自身能量来应对扰动，其示意图如图8 所示。

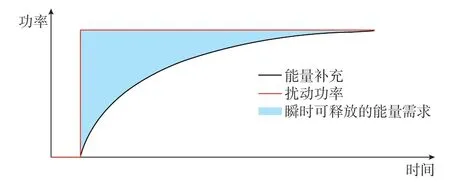
图8 存储单元瞬时可释放的能量需求示意图Fig.8 Schematic diagram of instantaneous release energy requirements of storage unit

存储单元的状态量表示其自身能量存储水平，存储单元的状态量在tn时刻下降到最低点xn时，存储单元释放的能量达到最大值。不等式xn＞xlimit可以转换为能量需求不等式 ΔEstorage(xn)＜ΔEb，max(J，xlimit)，其中，ΔEb，max为存储单元的瞬时可释放能量，其大小与惯量大小、状态量最大允许偏移量有关。进一步，结合最大允许的状态偏移量，可以得到对惯量的需求。

4.5 本地能量需求及评估方法

为使得务尺度的状态量不越限，除了每个尺度上的存储单元要有足够的瞬时可释放能量外，还要保证能够在能量流再平衡前维持住序贯响应后的准稳态。电力系统的能量流控制（即有功控制）是通过分散控制和集中控制相结合的框架实现的。初始右侧阀门的输入由集中式控制按照发电曲线给定；扰动施加在左侧阀门上，通过一系列有差的反馈控制，达到准稳态；最后，在一定时间内通过集中控制，重新调整右侧阀门的燃料输入，达到新的平衡。与传输通道的能量补充因通道惯量而具有滞后性类似，由于集中控制存在通信延迟，且承担集中控制的机组也有响应延时，故集中控制具有滞后性，整个能量供应链需要具备足够的能量来维持集中控制到位前对分散控制的有效支撑。这一能量需求实质上是对能量供应链本地存储能量的需求。

集中控制通过自动发电控制（automatic generation control，AGC）调用二次燃料实现，假设AGC 在Tn4时刻开始响应，经过Ts4时间完成调节，则总响应时间TAGC=Tn4+Ts4。假设在集中控制期间，AGC 机组的功率随时间线性变化，则本地能量需求可近似表示为图9 所示梯形区域面积，其大小为(TAGC+Tn4)ΔPD/2。

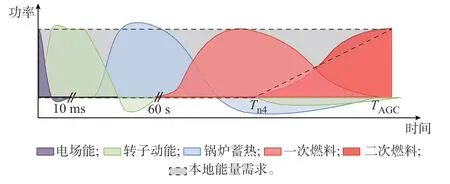
图9 本地能量需求示意图Fig.9 Schematic diagram of local energy requirements

本地能量可由锅炉蓄热提供，也可由燃料提供，整个动态的能量平衡方程可表示为：

式中：ΔPd∞为扰动在准稳态电压、准稳态频率和其对应的阻尼效应作用下的功率变化量；LΔI2L/2+TvΔPm+K1TfΔrb表示3 个传输通道的能量变化，CbΔpd表示锅炉蓄热提供的本地能量，则表示通过调用燃料提供的本地能量。

总的来说，系统对惯量的需求本质上是对能量的需求，并且可分为两部分：1）对务尺度而言，为保证状态量不越限而对存储单元瞬时可释放能量的需求；2）对总尺度而言，为保证对分散控制的有效支撑而对本地能量的需求。未来新型电力系统必须保证这两部分能量的来源充足，以保证系统在有功扰动下的能量流再平衡动态过程安全稳定。

5 考虑新能源并网的能量供应链

由于新能源的能量来源与并网方式和同步机不同，在新能源并网的系统中，新能源与同步机分别表示为两条不同的能量供应支链，且二者共同构成了一条复合能量供应链。本文第2 章详细探讨了对同步机务尺度能量供应链的建模方法，新能源支链的建模可以采取类似的思路。在物理上，新能源可以建模为直流电容加蓄电池或直流电容加旋转元件的模型，前者表示电池储能和光伏，后者表示风机或飞轮储能，如图10（a）和（b）所示，对应的新能源支链示意图如图10（c）所示。进而，将新能源支链与原有同步机能量供应链连接起来，即可得到新能源并网的系统复合能量供应链，而新能源的并网模式决定了图10（c）中阀门4 和阀门Y 的控制方式。目前主流的新能源并网方式为基于锁相环的跟网型控制模式以及基于虚拟同步机的构网型控制模式。下面分别对其能量供应支链进行介绍。

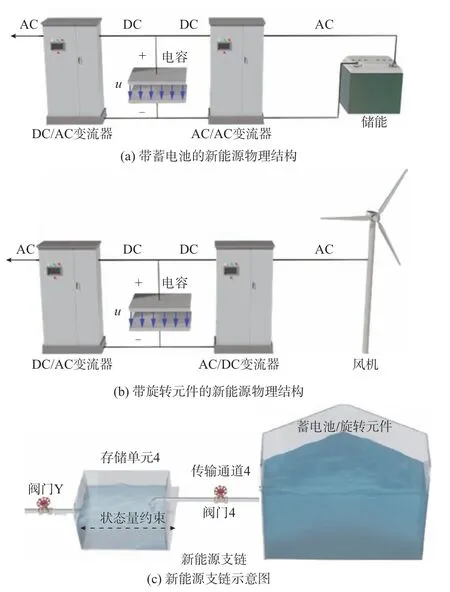
图10 新能源建模Fig.10 Modeling of renewable energy

5.1 跟网型新能源能量供应支链

当新能源采用基于锁相环的跟网型控制模式时，在有功扰动发生后，新能源的并网点电压发生变化，引起新能源的输出电流变化，但在新能源电流环的控制作用下，其输出电流在几毫秒内被控制到其原有参考值上，相当于使阀门Y 重新回到扰动前的状态，阻断了新能源对有功扰动的自然响应。

为了使新能源具备响应有功扰动的能力，基于锁相环获取的频率信息对阀门4 施加附加控制，使其在有功扰动后改变原有位置，从而改变新能源输出到系统中的能量流。目前，常见的附加控制包括虚拟惯量控制、下垂控制、快速频率响应控制等。从这几种控制方式的效果来看，虚拟惯量控制相当于增加同步机的M，而下垂控制和快速频率响应控制相当于增加KG和减小Tv。因此，在理想情况下，可将新能源的响应等效为同步机能量供应链参数的变化，但由于新能源具有运行工况时变、存在切换控制等特点，往往难以将其响应准确映射为同步机的能量供应链参数。

5.2 构网型新能源能量供应支链

与通过附加控制来响应扰动的跟网型新能源不同，构网型控制模式下的新能源具有自发响应有功扰动的能力。在当前研究中，最常见的构网型控制的实现方式是虚拟同步机控制。在此控制下，一旦系统发生有功扰动，新能源的阀门Y 将在网侧变流器的控制下持续抽取直流电容的能量，使新能源输出电流增大，而不是和跟网型新能源一样被电流环控制返回参考值。此后，直流电容电压下降，阀门4在机侧变流器的控制作用下抽取蓄电池/旋转元件中的能量来补充直流电容的能量。由于构网型新能源能够自发响应有功扰动，这意味着新能源支链能够在电磁尺度上起到与传统同步机相同的有功控制效果。在构网型控制下，新能源支链的内部响应被隐藏，其外特性表现为同步机特性，即新能源通过构网型控制模拟出虚拟的同步机支链，并建模为“惯量对”统一模型的形式。

6 结语

本文从惯量阻碍物体状态变化的物理本质出发，提出了电力系统广义惯量的概念，即系统不同能量环节抵御自身状态变化的能力，从而将电力系统惯量从机械旋转惯量扩展到涵盖系统能量供应所涉及的多个运动过程的惯量形式。

在广义惯量定义的基础上，本文根据尺度不同，将电力系统能量供应链划分为电气网络、转子汽机和锅炉燃料3 个子系统，并且务个子系统分别含有一个具有能量存储和能量传输作用的元件，两个元件的惯量组成一对“惯量对”，其大小共同决定该尺度子系统在扰动下的动态特性，并且由于系统在务尺度上的动态具有共性特征，可以建立“惯量对”统一模型用于统一描述。

在此基础上，将务尺度“惯量对”的统一模型依次连接并进行标幺化，形成了系统的多尺度能量供应链模型。基于该模型，揭示系统在严重事件扰动和随机负荷波动两种典型扰动场景下具有的多尺度能量供应链序贯动态特性和级联滤波特性。

然后，本文进一步讨论了能量视角下电力系统对惯量的需求。电力系统对惯量的需求本质上是对能量的需求，包含两个方面：一是在单一尺度上对存储单元瞬时可释放能量的需求；二是在总尺度上对用于支撑分散控制的本地能量需求。

本文依次从元件、子系统、能量供应链3 个层次对系统的能量供应过程进行建模和分析，不仅适用于传统电力系统，也可为未来新型电力系统能量供应链的建模与分析提供参考。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。